On-line diagnosis of mechanical defects of the combustion engine with principal components analysis

1. Introduction

As the computational techniques and the possibilities of simulation programs develop an increase of interest in creating models of dynamic processes and signals is noticed. Non-linear, complicated, of several degrees of freedom, models which complexity is only limited by the computational possibility of computers are being formed.

These methods are very useful in recognition of effects occurring in an engine, however they are difficult in application. In systems of on-line diagnostics the simpler methods – which would allow to differentiate good and faulty states as well as the defects identification – are constantly searched for. When the vibration signal is recorded several diagnostic parameters can be created on its bases. A part of them is useful and provides information of the object state, a part is correlated with other data, however there is also a part which disturbs the diagnostic process. In order to select parameters carrying information the method of the Principal Component Analysis (PCA) was applied forming the empirical model allowing for an automatic classification of mechanical defects on the bases of the vibration signal. The method was described in [1] and found an application in machine diagnostics [2-5]. Several aspects of its application in diagnostics of internal combustion engines are discussed in [6-8]. Mechanical defects of the combustion engine were diagnosed by authors with other techniques: autoregressive model [9], Kalman filter [10], Singular Value Decomposition of observation subspace [11]. This method aim is to supplement – already operating in vehicles – the On-Board Diagnostics (OBD) system (which detects emission faults) with mechanical defects diagnostics [12].

2. Description of experiment

Examinations were performed during road tests on the four-cylinder engine of spark ignition of Fiat Punto 1.4 of 400 000 km mileage. Series of engine vibration measurements for various rotational speeds and loads were performed. The main measuring path included the piezoelectric vibration sensors B&K Delta Shear type 4393 of a frequency range: 0.1-16500 Hz, resonance frequency 55 kHz and service temperatures from –74 to +250 °C, fastened by means of a joint screwed into the engine side at cylinder 1, and the portable device for recording data B&K PULSE type 3560E. Accelerations of engine block vibrations were recorded in the vertical and horizontal directions with a frequency of 65536 Hz, which means the frequency encompassing the sensor resonance frequency range.

Apart from the engine vibrations signal also the crankshaft orientation signal, throttle position and signals from the ignition coil at 1 and 4 cylinder were recorded. Additional signals enabled the identification of engine working cycles, injection moments, ignition and timing of gear phases.

Signals of about 1 minute duration were recorded during driving with a quasi-constant speed without rapid acceleration and deceleration.

Examinations were performed for various states of the engine [13]:

1) Engine in a good working order,

2) Defected head gasket,

3) Increased clearance of the exhaust valve (+0.06 mm),

4) Decreased clearance of the exhaust valve (–0.06 mm),

5) Exhaust valve out of order I (small defect), optimal clearance,

6) Exhaust valve out of order I (large defect), optimal clearance.

3. Selection of diagnostic parameters

The described above time signals recorded during a car drive became the basis for developing the observation matrix. The following parameters were applied: average value, RMS value, variance, skewness, kurtosis, max value, peak coefficient, impulse coefficient, shape coefficient.

These parameters can be calculated on-line, provided that the drive is with a relatively constant speed without rapid accelerations and brakes. Every parameter is determined in vertical and horizontal direction. Since the investigated parameters are characterised by a high variability from a cycle to a cycle, the numerical filter described by the recurrent equation was applied:

This expression is known as the Exponentially Weighted Moving Average Filter (EWMA). When used as a filter, the value of ${\stackrel{-}{x}}_k$ is again taken as the filtered value of $x_k$. The value of the filter constant, $F$ (0 $\le F<$1), dictates the degree of filtering, i.e. how strong the filtering action will be. When a large number of points are being considered, $F\to$1, and ${\stackrel{-}{x}}_k\to {\stackrel{-}{x}}_{k-1}$. This means that the degree of filtering is so great that the measurement does not play a part in the calculation of the average. On the other extreme, if $F\to$ 0, then ${\stackrel{-}{x}}_k\to x_k$ which means that virtually no filtering is being performed.

Variations of a root-mean square value (RMS) calculated for successive 200 cycles of engine works are presented in Fig. 1. This parameter was compared with the original data (Fig. 1(a)) and resampled into the crankshaft angle domain (Fig. 1(b)). Points denote RMS value calculated for the cycle, while a continuous line denotes values after recalculation by the EWMA filter with a factor $F=$0.6.

Since it is easier and faster to calculate on-line diagnostic parameters for the original data in the time domain, without their previous resampling, and the analysis indicated negligible errors at small fluctuations of rotational speeds, further operations were performed on the vibration signals in the time domain.

The matrix of training parameters $\mathbf{X}$, which columns constituted vectors of diagnostic parameters calculated in horizontal and vertical direction for one cycle of engine work, and rows – parameters in successive 200 measuring cycles for each engine state (1 no-fault state and 5 damage states mentioned above). In such way the matrix 18×1200 was obtained. Then the covariance matrix of training parameters was estimated from a dependence:

and the matrix decomposition according to own values was performed. Eigenvalues ${\lambda }_i$ and associated with then eigenvectors ${\mathbf{w}}_i$ are linked by:

Fig. 1RMS value for a) resampled data, b) data without resampling, c) changes of rotational speed during 200 working cycles of combustion engine

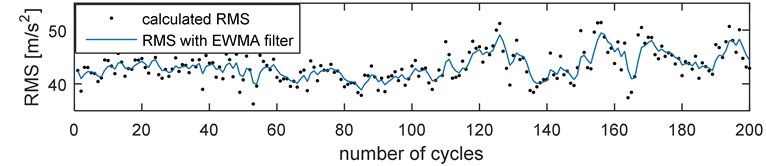
a) RMS value for data without resampling

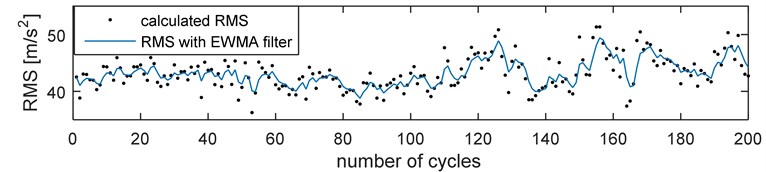
b) RMS value for resampled data

c) Instantaneous rotational speed

Fig. 2Classification of engine defects based on PCA, a) good technical condition, defected head gasket, defected exhaust valve (small), decreased clearance of exhaust valve, b) increased clearance of exhaust valve and defected exhaust valve (large)

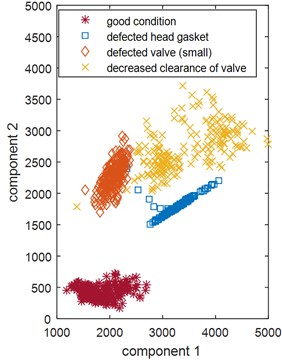
a)

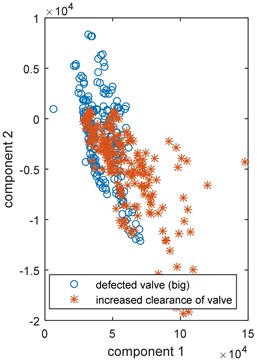
b)

Transformation of the principal component analysis (PCA) is a linear transformation, allowing to retain the most important information concerning the original process $\mathbf{x}$ in a reduced output data space $\mathbf{y}$:

where: $\mathbf{x}=[x_1,x_2,{\dots ,x_N]}^T$ – vector of data, $\mathbf{y}={\left[y_1,y_2,{\dots ,y}_k\right]}^T$ – reduced vector of data, $\mathbf{W}={[w_1,w_2,\dots ,w_k]}^T$ – transformation matrix.

On account of the domination of the first two eigenvalues ${\lambda }_1$ and ${\lambda }_2$ over the remaining ones, in further analysis the first two rows of the matrix $\mathbf{W}$ were used. It means the first two main components $y_1$ and $y_2$, determined from Eq. (4).

The classification of engine defects based on two main components is presented in Fig. 2. Four classes corresponding with technical states of the vehicle: no-fault state, decreased valve clearance, engine head gasket damaged, exhaust valve initial damage – are presented in Fig. 2(a). The classification was performed by the Support Vector Machine (SVM) method [3] and 99.1 % of differentiation was achieved. When the exhaust valve damage is growing the main components are changing, getting near and even overlapping factors obtained for the increased valve clearance (Fig. 2(b)).

Thus – in the proposed method – vectors ${\mathbf{w}}_1$ and ${\mathbf{w}}_2$ constitute the empirical diagnostic model of the engine. Their values are shown in Fig. 3.

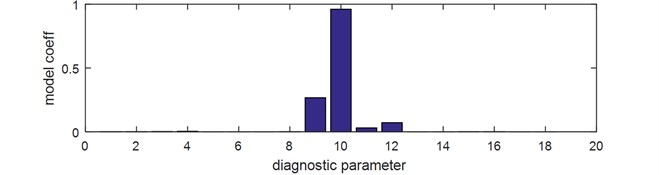
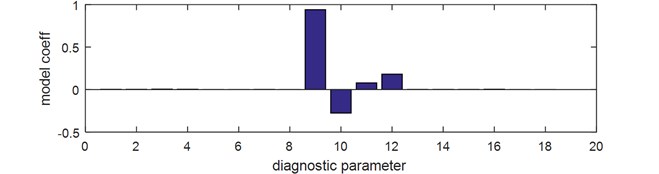
Fig. 3Model coefficients a) for 1 principal component, b) for 2 principal component. (Parameters: 1, 2 – average value (vertical, horizontal), 3, 4 – RMS value, 5, 6 – skewness, 7, 8 – kurtosis, 9, 10 – variance, 11, 12 – peak value, 13, 14 – peak coefficient, 15, 16 – impulse coefficient, 17, 18 – shape coefficient

a)

b)

It results from the analysis that the highest fraction in main components have variance and peak value. The procedure of selecting coefficients of the model Eqs. (2)-(4) was repeated for four parameters of the highest influence on the main components. For the new reduced model the classification result improved and equals now 99.4 % of correct hits for damages presented in Fig. 2(a).

4. Conclusions

The method of the preliminary recognition of defects of the internal combustion engine, which was verified for the Fiat Punto 1.4 engine with spark ignition, is presented in the hereby paper. The method uses statistic parameters of the engine vibration signal. Since it was noticed – when this method is applied – that resampling does not influence the classification result the original time signal can be used. This influences the implementation easiness and calculation speed, which is important during on-line diagnostics. The Principal Component Analysis (PCA) method was applied in order to reduce the diagnostic parameters vector. The influence of individual parameters on fractions of main components was analysed. The information redundancy was eliminated. It was pointed out that for the reduced vector of diagnostic parameters the classification result is even better than for the full vector taken into consideration previously. It was considered preliminarily to broaden the vector of parameters with central moments of higher degrees but this idea was abandoned due to a large variability of engine work cycles, which would cause an increased scatter of parameters inside the class and worsening of the classification quality. Scatters within classes can be decreased by increasing the value of factor $F$ of EWMA filter, loosing simultaneously instantaneous parameters changes. Finally the empirical statistic model was developed, taking into account 2 diagnostic parameters – variance and peak value in vertical and horizontal direction multiplied by weigh coefficients selected by means of the PCA method. This model allows to differentiate the no-fault engine technical state from 4 damage states with more than 99 % certainty. The model can be further developed to be suitable for recognition of other damages. The method was elaborated with the idea of supplementing the OBD system with the mechanical damages recognition on the basis of the vibroacoustic signal.