Combination of principal component analysis and time-frequency representations of multichannel vibration data for gearbox fault detection

1. Introduction

A problem of fault diagnosis in rotating machines has attracted attention of researchers for many years. In the literature one can find several comprehensive reviews on damage detection in gears and bearings [1-3]. Classical methods incorporate high-order statistics [4], empirical mode decomposition [5], wavelet transform [6], time-frequency domain analysis [7-9], bi-frequency analysis [1, 10]. Vibration signal from a machinery system is often a mixture of several source signals. For instance, a signal acquired on a bearing operating in a belt conveyor driving station, might be contaminated with vibrations of a gearbox located nearby or by vibrations caused by other damage [11-16]. Signal acquired on a gearbox revealing multiple damage is another example of a multi-source signal [15, 16]. In this paper we incorporate principal component analysis (PCA) for local damage detection in a two-stage gearbox operating in a belt conveyor driving station. The investigated data represents vibration acceleration of a single gearbox, measured at 4 different locations. PCA is performed on time-frequency representations of the signals. Additionally, performance of the proposed algorithm in comparison to single-channel analysis will be discussed. The method proved that integration of vibration signals from several channels provide a much clearer damage indication than a single signal does.

2. Methodology

In this chapter we will discuss the methodology that we applied to vibration signal from heavy duty gearbox operating in a belt conveyor driving station used in underground mining industry. The technique consists of several main steps.

In our analysis we take under consideration not the input signals directly, but the sets of four narrow-band slices from individual spectrograms of those signals.

First, the transformation of input channels into time-frequency representations (spectrograms) is performed. The spectrogram is a square of absolute value of the short-time Fourier transform (STFT) defined as follows:

where $w\left(t-\tau \right)$ is shifted window and $x_k$ is the input signal. In the next step we divide the time-frequency maps into narrow-band slices corresponding to given frequency bins. As a result of this step we obtain four dimensional sub-signals for each frequency band, since 4 channels are analyzed. Then we make use of Principal Component Analysis (PCA) [17-20].

Principal Component Analysis is one of the most common and widespread methods for multivariate linear data analysis. It serves for investigating data structure, data mining, data smoothing and approximation, also for exploring data dimensionality. The method permits to build new features, called principal components (PCs), which may serve for visualization of the data.

Let $\mathbf{X}$ of size $n$×$d$ denote the observed data matrix. For simplicity of presentation, assume that $n>d$, and that $\mathbf{X}$ is of full rank. It is advised to standardize or normalize the matrix $\mathbf{X}$. We assume that the data matrix is columnwise normalized. It means that all columns have means equal to 0 and variances equal 1/$n$. The PCA starts from computing the eigenvalues ($\lambda$) and eigenvectors ($\mathbf{v}$) of the cross-product matrix $\mathbf{S}={\mathbf{X}}^T\mathbf{X}$ satisfying the matrix equation $\left(\mathbf{S}-\lambda \mathbf{I}\right)\mathbf{v}=0$. This results in $d$ eigenvalues:

and $d$ eigenvectors associated with them:

The eigenvectors constitute the loading matrix $\mathbf{V}=[{\mathbf{v}}_1,\dots ,\mathrm{}{\mathbf{v}}_d]$. The two fundamental PCA paradigms are:

1) Feature construction:

The new features identified as columns of ${\mathbf{Z}}^{\left(K\right)}$ are called Principal Components.

2) Data reconstruction:

Taking $K=d$, the full original data matrix ${\mathbf{X}}_{n\times d}$ is reconstructed. For $K<d$ the best linear approximation of ${\mathbf{X}}_{n\times d}$ by a rank-$K$ matrix ${\widehat{\mathbf{X}}}_{n\times d}^{\left(K\right)}$ is obtained – it is best in the meaning of the $L^2$ norm.

The constructed PCs have the major advantage that they are uncorrelated, which permits to analyze each of them separately, without referring to the others.

Principal components can be also computed via Singular Value Decomposition (SVD):

where $\mathbf{Z}=\mathbf{U}\mathbf{D}$ e contains the PCs, and $\mathbf{V}$ the loading matrix.

For each of four-dimensional sub-signals ${\mathbf{X}}_{n\times K}^{\left(K\right)}$ we calculate PCA which returns four new features ${\mathbf{Z}}_{n\times K}^{\left(K\right)}$. Then we select the first component and insert it into a new array. As a result we obtain the new time-frequency map which consists of selected features corresponding to given frequency bands. At the end we aggregate the newly constructed time-frequency map into time domain to produce one-dimensional time series which is expected to contain cyclic impulsive components related to local damage.

Fig. 1The scheme of the introduced technique of local damage detection

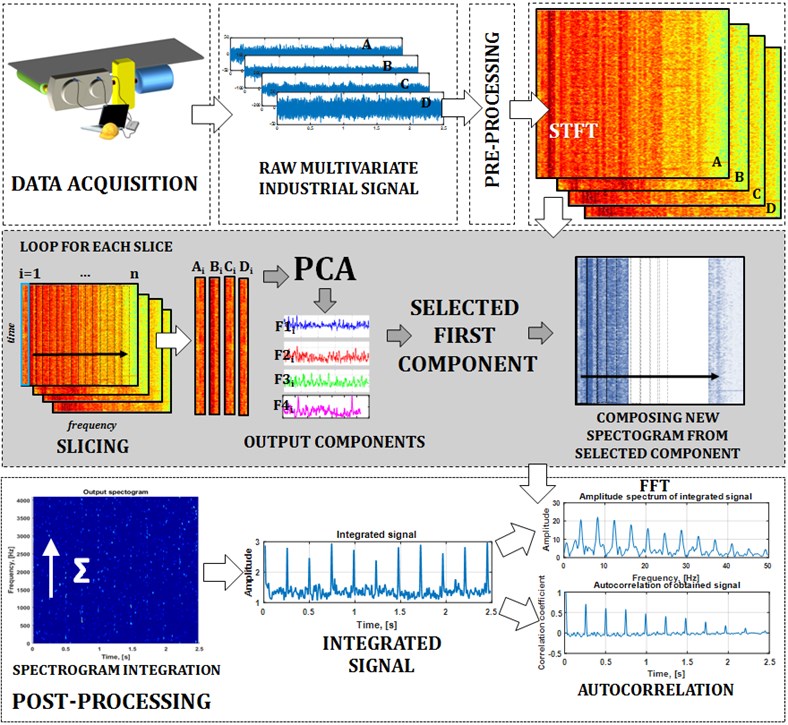
In order to detect cyclicity of the obtained time series we calculate spectrum and its autocorrelation function. We remind the autocorrelation of random stationary process $\mathbf{X}$ for time-lag $\tau$ is defined as:

where $E$ is the expected value operator and $\mu$, $\sigma$ are mean and standard deviations of $X$, respectively. Such spectrum can be considered as envelope spectrum since integration of the spectrogram returns information about signal energy flow and can be related to upper envelope of the signal. The scheme of the presented methodology is shown in Fig. 1.

3. Application to industrial data

3.1. Machine and experiment description

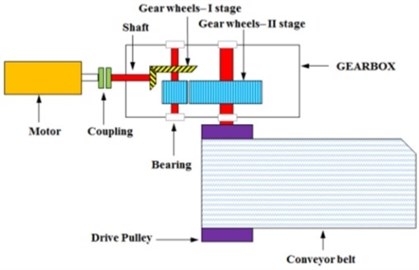
The machine considered here is a two-stage gearbox used in drive system for belt conveyor, see Fig. 2(a). Data used for validation of the method has been measured using accelerometers located on the gearbox housing (Fig. 2(b)) and the Brüel&Kjær system. The gearbox operates under stationary conditions, i.e. load and rotational speed are approximately constant. During the experiment four signals of equal duration have been acquired, each related to different sensor location (Fig. 2(b)).

Fig. 2a) Scheme of the investigated machine, b) location of sensors on gearbox housing

a)

b)

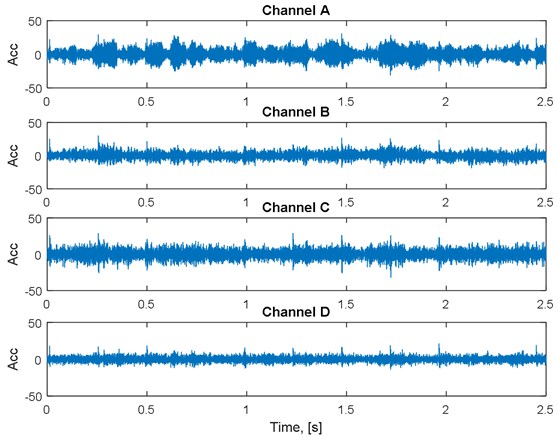
Fig. 3Multichannel input signal

The experiment shows that the gearbox does not reveal any damage. Thus, an artificial damage is introduced by specific signal processing technique in order to illustrate benefits of the proposed methodology. Namely, each of four acquired signals is considered as a response of the system (each signal stands for an individual system) to stationary noise, since there is no damage in the gearbox. Thus, we fit the autoregressive (AR) model to each of four signals by Yule-Walker equations and obtain four sets of coefficients called the impulse responses of the system. Orders of the AR models are high enough to reflect complexity of amplitude spectra of the acquired signals. Then, four pulse trains (Kronecker combs) with additive Gaussian noise are designed as excitation signals (source signals) that correspond to a damaged gearbox. Duration of the excitation signals is equal to the duration of signals acquired during the experiment. The fault frequency associated to damage in gear-wheel on the middle shaft is 4.1 Hz and this is the frequency of impulses in the pulse trains. The ratio of impulse to noise amplitudes is different for each excitation signal, which corresponds to different distance between each sensor and the damaged gear. Finally, the pulse trains are convolved with corresponding impulse responses and such signals are further analyzed and referred as “raw signals”.

3.2. Diagnostic data – raw multichannel signal

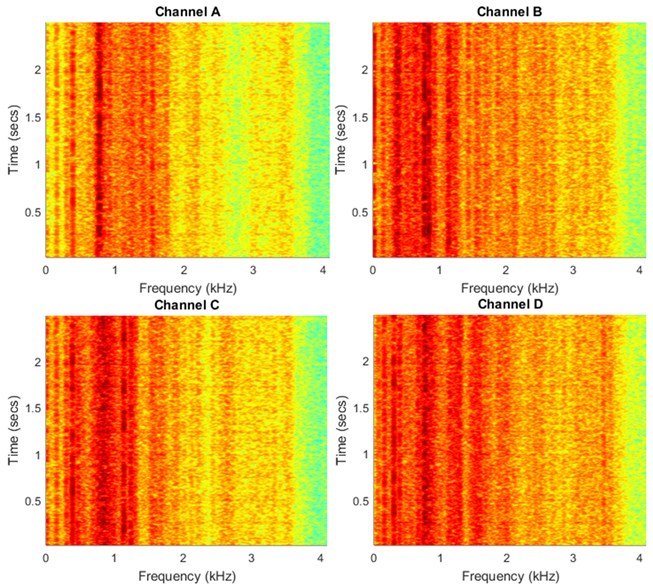
Raw multivariate (4D) signal considered here consists of four 2.5 s time series representing gearbox vibration under “normal” operation i.e. during transportation of bulk material. Frequency sampling is $f_s=$8192 Hz. Raw multichannel signal and its spectrogram representation is shown in Fig. 3 and 4, respectively. Both time series and their spectrograms allow to notice some weak wideband impulsive components but it is impossible to distinguish them unambiguously.

Fig. 4Spectrograms of the multichannel signal

3.3. Evaluation of the algorithm performance on industrial data

In this section we present the results of the introduced method, i.e. performance of the algorithm applied to the discussed industrial data. Fig. 5(a) presents new time-frequency map which consists of the components extracted by applying PCA to the sub-signals from the initial spectrograms. As we observe, the impulses (wideband excitations) are much more clear than in the spectrograms of the multichannel raw signal, see Fig. 4. Moreover, simple aggregation of 2D map into 1D vector by integration of energy for each time instance shows impulsive nature of energy flow. Using autocorrelation or simple spectrum one might identify period/frequency of impulse repetition that corresponds to fault frequency, see Fig. 5(b), (c).

It is also important to note that scores of principal components of slices from initial spectrograms vary in frequency domain. Although the first component was taken always, its score ranged from over 0.99 for heavily impulsive frequency bins, down to less than 0.6 for bins that do not carry as much impulsive information.

Fig. 5a) Output spectrogram composed of first PCA components, b) time series extracted from output spectrogram, spectrum of integrated time series and c) autocorrelation function of the integrated time series with its spectrum

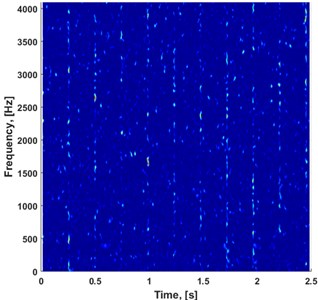
a)

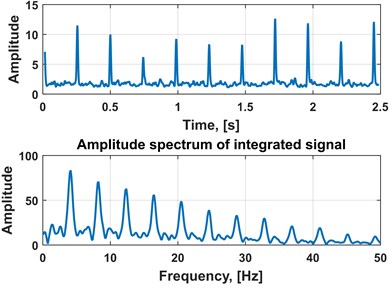
b)

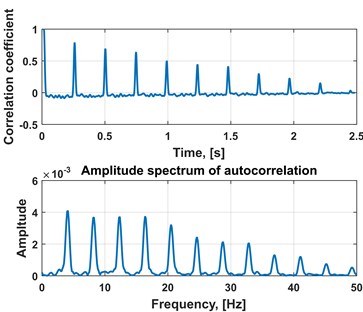
c)

3.4. Comparison with hypothetical individual channel processing

It is very important to justify the benefits of presented method in comparison to results of analogous approach applied to individual channels separately. For one channel we can only calculate the spectrogram and then aggregate it, since there is no multidimensionality to begin with. We have done this for four input channels. Fig. 6 presents comparison of the results with the output of our multichannel method. It is clear that the multichannel analysis is undoubtedly beneficial. As a measure of impulsiveness we chose kurtosis, which is widely appreciated as a standard indicator of signal impulsiveness. The empirical kurtosis for vector of observations $x_1$, $x_2$,…, $x_N$ has the following form:

8

$\widehat{k}=\frac{\frac{1}{N}{\sum }_{i=1}^N{\left(x_i-\stackrel{-}{x}\right)}^4}{{\left(\frac{1}{N}\sum _{i=1}^N{\left(x_i-\stackrel{-}{x}\right)}^2\right)}^2}.$

Kurtosis values of individual channel outputs and multichannel procedure output are presented in Table 1.

Table 1Comparison of kurtosis values for individual channels vs. multichannel procedure

Channel	Kurtosis
1	4,06
2	6,15
3	10,34
4	7,82
Multichannel	22,83

Fig. 6Comparison of single channel analysis vs. proposed multichannel method (all normalized by scaling down to value range 0-1). Panels a)-d) show outputs for every channel separately, and panel e) presents output signal from our method

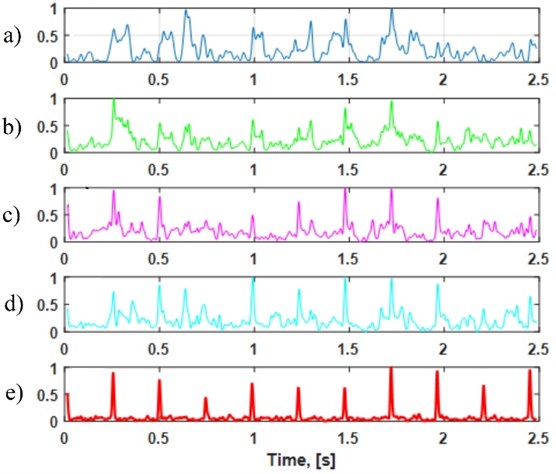
4. Conclusions

In this paper we have introduced a new method of local damage detection applied to the real vibration signal from heavy duty gearbox used in mining industry. This methodology is based on the analysis of multichannel time series and its representation in time-frequency domain (spectrogram). In order to extract information about the damage we analyze the features obtained by applying PCA to four-dimensional sub-signals corresponding to given frequencies on the spectrogram. The introduced technique applied to vibration signal gives much better results than the classical methods based on the analysis of one-dimensional vibration signal. By using the methodology cyclic impulses might be clearly noticed which allows to relate them with the damage. We should mention, that the proposed algorithm is automatic and can be applied to other vibration signals for which the classical methods do not provide desired results.