Simulation studies of a shock absorber model proposed under conditions of different kinematic input functions

1. Introduction

Automotive vehicles are driven on roads of diversified pavement condition. A road profile may theoretically take different deterministic and stochastic forms, however in practice, only with regard to special testing sections of road, one may assume that pavements can be described by means of unique mathematical functions [1-5]. Under actual conditions of road pavements on which automotive vehicles run, the most convenient method is to characterise the road profile by means of power spectral density of irregularities. In such a case, it is envisaged that recording of the irregularity profile creates a stationary and ergodic process. Recording a road profile with the linear speed of 1 m/s allows for the spectral density of irregularities to be represented in the function of e.g. irregularity wavelength $L_n$ m. A car running on the given road is subject to input functions depending on the pavement condition as well as the current driving speed. Power spectral densities of road pavement irregularities may be represented as functions of frequency having previously taken an additional parameter of driving speed into consideration. In accordance with the applicable standards, the road profile is described through a set of points of road irregularity height measured along the trace of cooperation between the vehicle’s right wheel and the road pavement. Measurements of road pavement irregularity heights are recorded with a constant interval of the road longitudinal length equalling 0,1 m. An irregularity profile thus recorded provides grounds for calculation of the longitudinal irregularity parameters. Based on the irregularity profile, one calculates a set of longitudinal road roughness parameters, the most important of which is IRI (International Roughness Index). What one applies in simulation studies for modelling of road irregularities is the road irregularity models defined in the ISO 8608 standard, where power spectral densities of road irregularities in the form depicted in Fig. 1 are used to describe the profile.

Fig. 1Classification of road irregularity profiles in accordance with ISO 8608

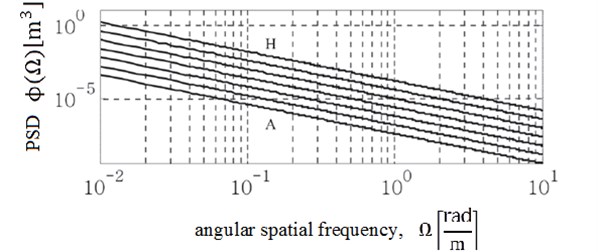
A road of the best quality (smallest irregularities) is marked with the letter A. The worse the road pavement condition is, the further the designating letter is in the alphabet, with H marking the worst road quality. A problem difficult to solve in terms of an automotive vehicle operation is to diagnose a shock absorber installed in the suspension system. The main function performed by a shock absorber is connected with limiting relative movements of the sprung as well as the unsprung mass. The essence of the problem is that, despite the relatively simple design, a car shock absorber is a component of complex non-linear dynamic properties. The paper addresses results of simulation studies conducted using a dedicated diagnostic shock absorber model developed. The shock absorber model in question was introduced into a quarter-vehicle suspension system model whose other parameters were selected based on an analysis of the actual automotive suspension system.

2. Simulation studies

With reference to previous studies undertaken by the authors, a mathematical shock absorber model was developed, entailing the apparent shock absorber elasticity and defining damping characteristics as a two-argument function.

The strong dependence of the damping characteristics for the working stroke length determines the need to take this phenomenon into account in computational models of automotive shock absorbers [6-8]. The relationship describing this phenomenon is generally as follows:

where: $v$ – current velocity of input, $w_s$ – total length of the working stroke.

Characteristics of stiffness of the shock absorber force is a function of frequency and displacement. Thus the seeming stiffness of the damper can be described as:

where: $d$ – displacement, $f$ – frequency.

The mathematical notation of the shock absorber model is as follows.

The value of damping force $F_D$ in the conceptual shock absorber model can be determined by interpolation:

where: limits $a$, $b$, $c$ and $d$ are determined empirically.

The approximation of function values $F_D$ for any arguments:

is made for the known values – interpolation nodes which are the results of measurements:

where: $a\le v_0\le v_1\le v_2\le \dots \le v_n\le b$ and $c\le w_0\le w_1\le w_2\le \dots \le w_m\le d$ using a spline functions.

The force of the resulting damper stiffness $F_{ss}$ reads:

where: limits $a$, $b$, $c$ and $d$ are determined by experimental approximation of function $F_{ss}$:

for interpolation nodes:

where: $a\le d_0\le d_1\le d_2\le \dots \le d_n\le b$, $c\le f_0\le f_1\le f_2\le \dots \le f_m\le d$.

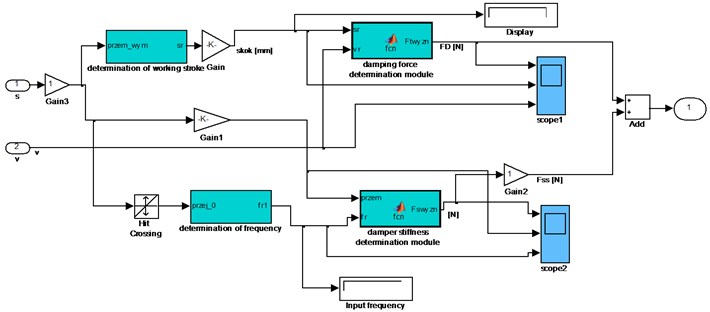
The simulation studies addressed were conducted using the Matlab/Simulink program. The suspension system model developed, with a detailed shock absorber diagnostic model implemented, has been illustrated in Figs. 2 and 3.

Fig. 2Computational model of suspension used in the simulation studies

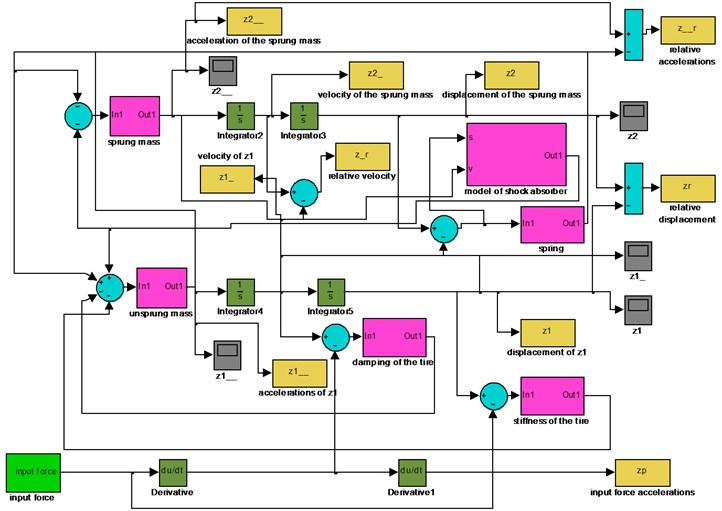
Fig. 3The shock absorber model

The studies included application of different random kinematic input functions generated for the given running speed using the spectral description of pavement irregularities provided in Fig. 1.

3. Research results and their analysis

The aim of the study was to analyze the forces generated in a detailed model of the dynamic damper built-in suspension of the vehicle. Examples of kinematic input used in the simulation tests is shown in Fig. 4.

Fig. 4The example of input force generated by road roughness

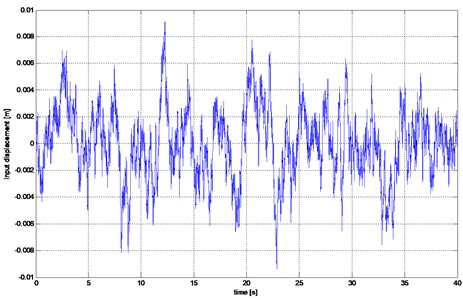
Fig. 5The results of simulation studies for good road

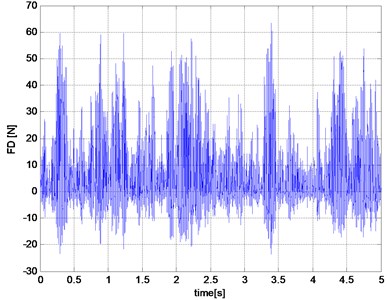
a) The damping force

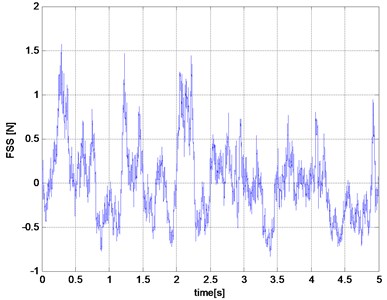
b) The spring force

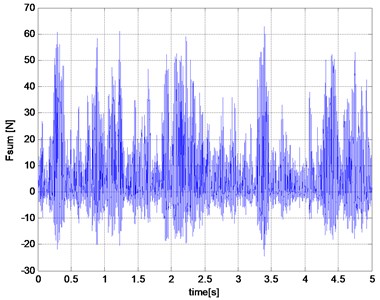
c) The total force of shock-absorber

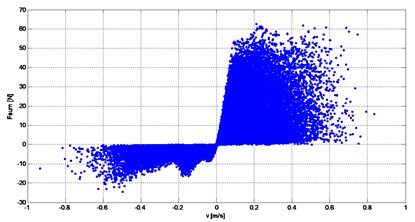
d) Total force of shock-absorber for the velocity

Input of road roughness can be interpreted as a kinematic input to the computations dynamic model. The work of damper exhausted in turn derived from to force dynamic unsprung mass. This is because the damping force affects the movement of the wheels and thus occurs between shock and unsprung mass interaction. Relative movement of the sprung and unsprung masses are the primary cause of the forces in the damper. The scope of the forces generated by the shock absorber is wide. Examples of results of research work suspension damper model are presented in Figs. 5-6.

Fig. 6The results of simulation studies for bad road

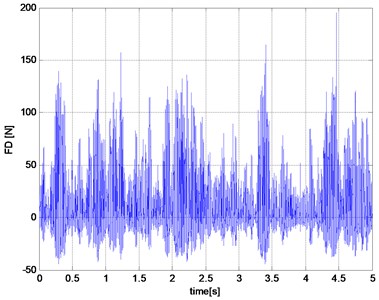
a) The damping force

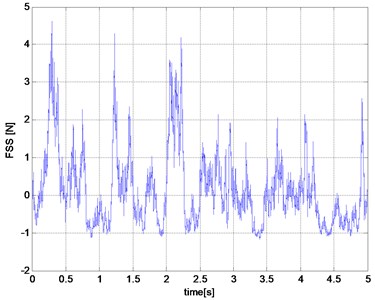
b) The spring force

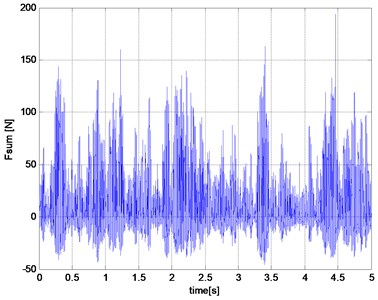
c) The total force of shock-absorber

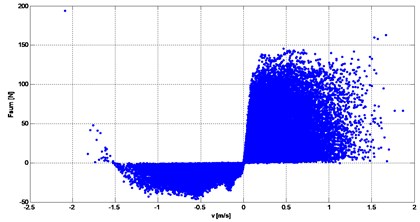
d) Total force of shock-absorber for the velocity

The larger the road surface roughness including greater operating range automotive shock absorber [9, 10]. Work damper improves the comfort and safety. The model allows us to analyze complex phenomena associated with dampened suspensions vehicles.

4. Conclusions

The study of mechanical systems with nonlinear damping are the subject of numerous scientific papers. The diagnostic tests simulation assumed that the mathematical model should be compatible with the real object. In the cited study we used the results of the developed model of automobile shock absorber. Analysis of the images work damper allows for the development of specific measures of a technical condition. Based on the results achieved can, going one step further, to develop a method of diagnosing shock absorbers under their normal operation. That task will be the subject of further work of the authors.