A procedure for total knee alignment prosthesis using the ICP algorithm in the aim to implant it in the biomechanical engineering

1. Introduction

In mechanics, the design and the optimal manufacture of surgical implants are strongly related to the surfaces quality, which is one of the most important parameters in the manufacturing process, since it represents the final step in the cycle of production to improve the quality degree of implants surfaces. Generally, the knee prosthesis is constituted of three parts. Two metal parts are fixed respectively on the femur and the tibia and a third known as intercalated made up of a very strong plastic resistant called the polyethylene, which improves the knee slip.

In orthopedic surgery, to obtain an optimal positioning of the knee implant installation, the surgeon must use different reference marks at the same time and cut the worn out zones in bones and replace them with metal or plastic parts; these will be fixed with or without cement. Therefore, it is very important in the knee prosthesis installation to have instruments that make it possible to work both in a conventional way $\text{(}x$-ray) and as computer-assisted [1]. However, the computer-assisted navigation is a technique which makes it possible to improve the precision of the setting in best position of the knee prostheses. Moreover, it’s recognized more and more that the technology of computer-assisted navigation significantly increases the precision of installation of total knee prostheses; and it is only recently that one recognized the importance of an instrumentation of precise revision dedicated to the resumptions of total knee prostheses [2]. However, a navigation application conceived specifically for the needs of the revision surgery of total knee prostheses has not been and still isn't available until now.

The objective of the research work presented in this paper, is to provide an assistance tool to the alignment of total knee prostheses, by using the improved ICP algorithm (Iterative Closest Point) in order to contribute to the improvement of the current techniques.

2. Presentation of the iterative closest point algorithm

The ICP algorithm is a well-known method for registering a 3D set of points to a 3D model [3]. Since the presentation of the ICP algorithm by Besl and McKay (1992), many variants have been introduced. The new propositions affect one or more stages of the original algorithm to try to increase its performance, specially accuracy and speed. This method minimizes the sum of squared residual errors between the set of points and the model. The ICP algorithm finds a registration that is locally the best fit using the least-squares method [4]. Its main goal is to find the optimal rigid transformation which will correspond as well as possible to a set of measured points (P) to a geometrical model (M). The parameters of the rigid transformation between the sets of points $P^I$ and $P^{II}$ must minimize the cost function Fig. 1.

Fig. 1Principal steps of the I.C.P. algorithm

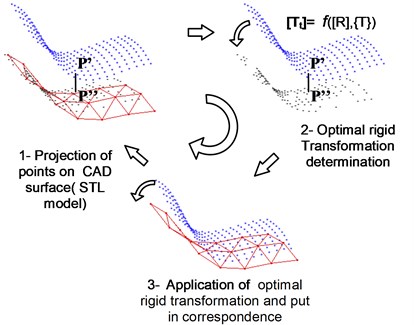
A rigid transformation $T_t$ consists in the rotation matrix [$R$] and the translation vector $\left\{T\right\}$ giving the iterative transformation $P_i^{II}=\left[R\right]\times P_i^I+\left\{T\right\}$ ($P_i^I$ will be transformed into a point $P_i^{II}$). The ICP algorithm usually needs a good initial estimate of the initial parameters $\left({\left[R\right]}_0,{\left\{T\right\}}_0\right)$ for the purpose of convergence. For that, this algorithm requires an initial estimate of the registration; because the computation speed and registration accuracy depend on how this initial estimate is chosen [5]. In this algorithm, we have to determine the six degrees of freedom including the three for rotation and the other three for translation by ICP. While the three dimensional translation vector has simply three parameters as $\left\{T\right\}={\left[tx,ty,tz\right]}^T$, the rotation matrix is apparently composed of nine elements which should go along with six conditions for orthonormality. A simple iterative optimization based on the least square principle can’t guarantee this orthonormality. Hence, improved ICP employs unit quaternion $\left(q_0;q_1;q_2;q_3\right)$ for representing the rotation parameters in order to reduce this problem.

3. Improved test using industrial application

In this application, the manufacturing parts using the rapid prototyping technology is treated (Fig. 2). The machine used on this application is based in the Fused Deposition Modeling technical. This process is used to manufacture the real part starting from an STL format file obtained by the Computer Aided Design (CAD) software [6], which approximates the shape of a part using triangular facets The manufacturing of parts, by the prototyping technology, consists of the reproduction of the STL model by deposit of plastic at a hot temperature [7] with the temperature of the print head nearing 250 °C.

It will be noted here, that the STL model is composed of nodes, edges, and triangular facets [8]. Each facet has a normal vector; and that each triangle has a neighbor along each edge; and these are authorized to intersect only along one edge or on a node. The CAD software which produces the STL format doesn’t mention the fact that the facets can be intersected incorrectly and that the same edge can be divided by more than two facets. The triangular facets also can be piled; in this case the defects can only be detected during the prototyping process.

Fig. 2Prototyping technology process

In the acquisition phase a machine equipped with a coaxial optical sensor (CHR 150) is used, which gives the real surface topography. The two models being defined we can now call upon the alignment program of the theoretical set of cloud points with the triangulated surface. The obtained results are presented in Fig. 3.

Fig. 3Results of computation using ICP algorithm

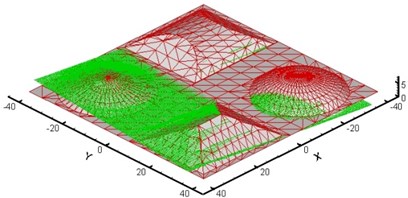
a) Initial estimate

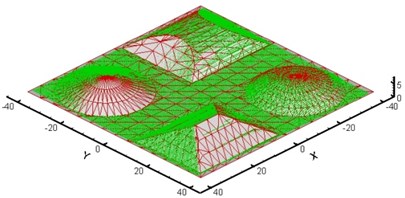
b) Final adjustment

The total error approximation is given by the following function:

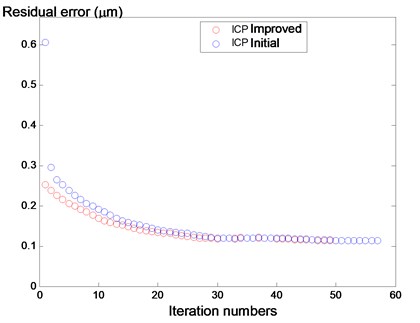
In Fig. 4, total error approximation $e\left(R,T\right)$ is represented, and corresponds respectively to the traditional ICP algorithm and improved ICP, according to the iteration number.

The comparison between the two curves shows that on the one hand the error generated by the improved ICP is less than the error generated by the traditional ICP; and the traditional ICP converges after 57 iterations; comparatively to the improved ICP who converges after 48 iterations.

Fig. 4Total approximation error

4. Alignment knee prostheses using ICP algorithm

The geometry of the knee bone is first obtained from a medical scanner, using a sweeping of a theoretical plan according to the longitudinal direction “$z$” a cloud points representing the knee bone topology (Fig. 5) can be recovered. Each point is represented at least by its coordinates $x$, $y$ and $z$.

Fig. 5Cloud points of knee bone topology

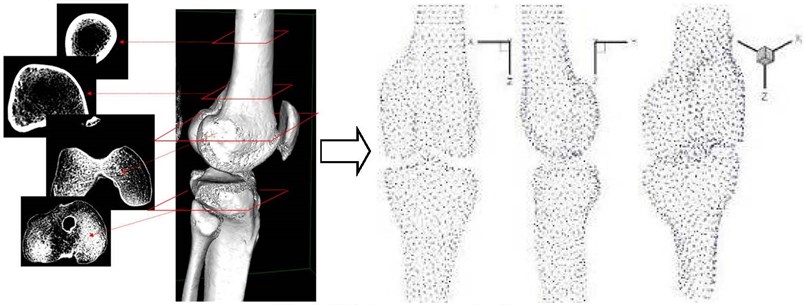
A preprocessing of the acquisition data is necessary, since they cannot be used directly: they present a noise measurement, useless environment data…etc. They must therefore be treated in order to be usable. Once the data treated, they can be triangulated, to pass from a cloud points to an STL model which generally requires a dense and homogeneous cloud. This configuration will be stored in a patient database which will be reusable in the alignment step. Moreover, to this, the orthopedic surgeon can use it in the knee bone preparation step, to define the angles of cut plans (Fig. 6) [9]. It will be necessary to remove the damaged cartilage in addition to a few millimeters of the bone not infected. At the tibia level, the cut is in general plane and horizontal; on the femur several cuts are necessary to prepare the bone. These cuts must be calculated precisely, to adapt the selected prosthesis model as accurately as possible [10].

Fig. 6Bone preparation [9]

Once the bone surface is prepared, after the cut step; the surgeon installs a test prosthesis to experiment the various movements of the knee and the balance of its various ligaments. Some adaptations can then be realized, before the fixing of the final knee prosthesis. The fixing can be done with or without cement according to the prosthesis type and of the bone state, with an aim of obtaining the best result. In this step, the surgeon can use a computer, and thanks to sensors positioned on the femur and tibia, he will be able to calculate the guided osseous cuts with the assistance of computer-assisted system surgery (CAD).

To test the alignment step the adopted principle is easy; we apply a displacement to the co-ordinates of cloud points to simulate measurement errors (Fig. 7). By the application of a rigid transformation, the final transformation provided by the program realises alignment between the cloud points and the surface in STL format. The program reliability is tested by considering two principal factors: the convergence and the necessary time for the program to be executed.

Fig. 7Evolution of the total error

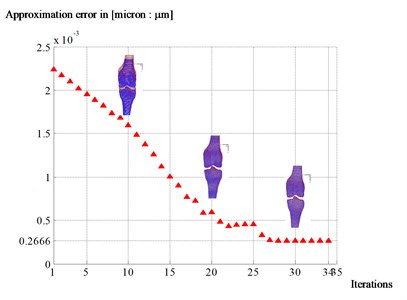
Fig. 7 shows that the program converges quickly on a stable solution after 25 iterations and that the total error is equal to 0.2666 [µm] which is very acceptable for this type of applications [11].

5. Conclusion

The knee osteoarthritis is purely a mechanical problem; neither treatment, nor rehabilitation can truly cure this type of disease. The articulation becomes increasingly stiff and painful and the patient walking becomes very difficult. The situation can worsen; it is useful to consider a surgical operation where the orthopedic surgeon proposes to replace the articulation of the knee by a partial or total prosthesis.

Over the last few years, the development of manufacturing process has covered all automated production phases, from design to the parts inspection passing by manufacture. The design and the manufacture of complex surfaces has become common practice in the mechanical industry. This development, which is considered to be a large progress in the design and optimal manufacture process of the prostheses, will make it possible from now on, to tackle as well as achieve normal knee functionality.

The computer-assisted navigation technique used in the knee prosthesis installation improves the precision of this installation and constitutes a real improvement of the orthopedic surgery [1]. It is proposed through this work that an assisting tool to the alignment of total knee prostheses is provided as a contribution. The method used is based on the iterative-closest-point (ICP) algorithm, which is a well-known method for registering a 3D set of points to a 3D model that minimizes the sum of squared residual errors between the set and the model [12].