Stability of initialization response of fractional oscillators

1. Introduction

Viscoelastic materials have gained broad applications in structural vibration control engineering, including aerospace industry, military industry, mechanical engineering, civil and architectural engineering [1]. To characterize the rheological behavior of viscoelastic materials, application of fractional calculus representations (shortly termed as fractional constitute relations) becomes an effective and powerful technique.

Fractional oscillators, or fractionally damped structures, are systems where the viscoelastic damping forces in governing equations of motion are described by fractional constitutive relations [2]. The significance of study on fractional oscillators lies in the following two aspects. In engineering practice, mechanical models for various viscoelastically damped structures are simplified to single-degree-of-freedom or multi-degree-of-freedom oscillators. On the other hand, investigations on typical oscillators provide theoretical basis for dealing with intricate mechanical systems. Recently, researches on fractional oscillators are mainly focused on theoretical and numerical analysis of the vibration responses. In [2, 3], dynamical responses of single-degree-of-freedom linear and nonlinear fractional oscillators, multi-degree-of-freedom fractional oscillators and infinite-degree-of-freedom fractional oscillators have been reviewed. Asymptotically steady state behavior of fractional oscillators has been studied in [4, 5]. Based on the functional analytic approach, criteria for the existence and behavior of solutions have been obtained in [6-8], and particularly the impulsive response function for the linear SDOF fractional oscillator has been derived. Moreover, the asymptotically steady state response of fractional oscillators with more than one fractional derivatives have been analyzed in [9].

Due to the fact that both of the mechanical property and the fractional derivative operator are characterized by memory effect, research on the memory or historical effect of fractional oscillators is an important issue. There are generally three initialization approaches to describe the memory effects of fractional operators or fractional systems: the history function approach [10, 11], the initialization function approach [12, 13], and the infinite sate approach [14, 15]. On the basis of the history function approach, initialization response of single-degree-of-freedom fractional oscillators has been investigated in [11]. Based on the initialization function approach, initialization response of general fractional systems has been studied in [16]. In [17, 18], initialization response of fractional systems with ramp history function and constant history function have been studied based on the infinite sate approach. All the above results have been shown that different external exciting forces generate different initialization responses.

Our main objective in this paper focuses on the effect of the initial conditions on dynamical stability of fractional systems. The memory effects or historical effects on dynamical responses in fractional oscillators is firstly investigated via numerical simulations. Then the stability of initialization response is proved based on the unit impulse response function and the Lyapunov stability theorem for fractional differential equations. Our main conclusion is that the stability of initialization responses of fractional oscillators is irrelevant to initial conditions or prehistory.

2. Historical effects on dynamical response of fractional oscillators

We assume that the dynamical response before the initial instance is $x_{in}\left(t\right)$ due to external exciting force$f_{in}\left(t\right)$, and after $t=0$ the external force imposed to the fractional oscillators is $f\left(t\right)$. More compactly, the external exciting force is denoted by $v\left(t\right)$:

Taking the above prehistory into account, the differential equation of motion for single-degree-of-freedom fractional oscillators is:

where ${}_0{}^{}{D}_t^{\alpha }$ is the initialized fractional derivative operator: ${}_0{}^{}{D}_t^{\alpha }x\left(t\right)=\underset{a\to \mathrm{\infty }}{\mathrm{l}\mathrm{i}\mathrm{m}}{}_{-a}{}^{}{D}_t^{\alpha }x\left(t\right)$.

On the other hand, in terms of the initialization function approach [12, 13], we have:

where ${}_0{}^{}{d}_t^{\alpha }$ is the uninitialized fractional derivative, $\psi \left(t\right)$ is a time-varying initialization function accounting for the effects of the past.

Substituting Eq. (2) into Eq. (1), we obtain:

Remark 1. In the case where the fractional oscillator is at rest before $t=0$ and excited by the external force$f\left(t\right)$ after $t=0$, the differential equation of motion is:

where ${}_0{}^{}{D}_t^{\alpha }x={}_0{}^{}{d}_t^{\alpha }x$.

Due to the fact that both of the mechanical property and the fractional derivative operator are characterized by memory effect, we declare that the dynamical response of the fractional oscillator is influenced by the historical exciting force $f_{in}\left(t\right)$ or vibration motion $x_{in}\left(t\right)$ in prehistory. As a result, different historical exciting forces generates different dynamical response. In mathematics, different vibrations $x_{in}\left(t\right)$ in prehistory (even if $x_{in}\left(t\right)$ at $t=0$ is same) generates different initialization function $\psi \left(t\right)$ and different dynamical response.

In the following, we provide numerical simulations to clarify this statement. We assume that the fractional oscillator is at rest before $t=-a$, in the historical period $\left[-a,0\right]$ the dynamical response is $x_{in}\left(t\right)$, and after $t=0$ the fractional oscillator is excited by the external force $f\left(t\right)$. The differential equation of motion is:

In the numerical simulation, the mass, damping coefficient and stiffness coefficient in Eq. (4) are taken respectively as $m=\mathrm{}$1, $c=\mathrm{}$0.4, $k=\mathrm{}$2, the order of the fractional derivative is $\alpha =\mathrm{}$0.56, the external exciting force is assumed as $f\left(t\right)=30\mathrm{c}\mathrm{o}\mathrm{s}6t$, the history period is [–4, 0]. The vibration motion in prehistory is assumed to be $x_{in}\left(t\right)=A\mathrm{s}\mathrm{i}\mathrm{n}\left(\pi t\right)$. Taking the amplitude$A$ respectively as $A=\mathrm{}$10, $A=\mathrm{}$5, the dynamical response is different as is depicted in Fig. 1.

Fig. 1Different responses induced by different prehistories

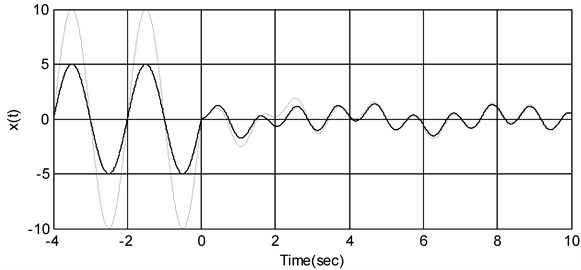
Remark 2. For the following classical integer-order single-degree-of-freedom oscillator:

The dynamical response is irrelevant to the vibration motion in prehistory and it only depend on the initial displacement $x_0$ and the initial velocity ${\dot{x}}_0$. This property is clear from the local property of integer-order derivatives.

3. Stability of initialization response of fractional oscillators

The initialization response of fractional oscillators is the dynamical response of the open-loop system of Eq. (3), i.e. when the external force $f\left(t\right)=0$ after $t=0$. The mathematical model for the open-loop system is:

where $x_{OL}\left(t\right)$ is the displacement.

Different exciting force $f_{in}\left(t\right)$ or vibratory motion $x_{in}\left(t\right)$ in prehistory generate different initialization responses. In the following we clarify this phenomenon via numerical simulations.

In the numerical simulation, the mass, damping coefficient and stiffness coefficient in Eq. (6) are taken respectively as $m=\mathrm{}$1, $c=$ 0.4, $k=$ 2, the order of the fractional derivative is $\alpha =\mathrm{}$0.56, the history period is [–4, 0]. The vibration motion in prehistory is assumed to be $x_{in}\left(t\right)=A\mathrm{s}\mathrm{i}\mathrm{n}\left(\pi t\right)$. Taking the amplitude $A$ respectively as $A=\mathrm{}$10, $A=\mathrm{}$5, the dynamical response of the open-loop system Eq. (6) is depicted in Fig. 2.

Fig. 2Different initialization responses induced by different prehistory

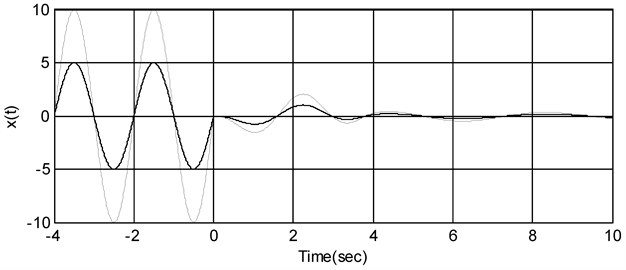
However, we declare that whatever the external exciting forces $f_{in}\left(t\right)$ or vibratory motions $x_{in}\left(t\right)$ in prehistory are, the initialization responses $x_{OL}\left(t\right)$ are always stable. We prove this conjecture in the following.

Theorem 1. For the single-degree-of-freedom fractional oscillators Eq. (1), the dynamical stability of the initialization response is irrelevant to the external exciting force or vibratory motion in prehistory.

Proof: Firstly, we decompose the dynamical response $x\left(t\right)$ of system Eq. (1) into two parts: one is the zero input response $x_{zi}\left(t\right)$ (also termed as the initialization response $x_{OL}\left(t\right)$) and the other is the zero state response $x_{zs}\left(t\right)$, i.e., $x\left(t\right)=x_{zi}\left(t\right)+x_{zs}\left(t\right)$.

where the zero input response $x_{zi}\left(t\right)$ follows that:

and where the zero state response $x_{zs}\left(t\right)$ follows that:

The main objective is to prove that the initialization response of fractional oscillator Eq. (1) will asymptotically converge to zero, i.e. $x_{zi}\left(t\right)\to 0$ as $t\to \mathrm{\infty }$.

Eq. (7) is rewritten as:

where:

The solution of Eq. (7) is decomposed into $x_{zi}\left(t\right)=x_1\left(t\right)+x_2\left(t\right)$, where $x_1\left(t\right)$, $x_2\left(t\right)$ satisfy the following Eq. (9) and Eq. (10) respectively:

In terms of the impulse response function for fractional oscillators provided in [8], we have:

where $K\left(t\right)$ is the solution of $\left(m{D}^2+c_0{D}_t^{\alpha }+k\right)K\left(t\right)=\delta \left(t\right)$.

Furthermore, $K\left(t\right)$ is decomposed into $K_1\left(t\right)$ and $K_2\left(t\right)$: $K\left(t\right)=K_1\left(t\right)+K_2\left(t\right)$. Where $K_1\left(t\right)$ and $K_2\left(t\right)$ follows that:

Because $x_{in}\left(t\right)$ is bounded, we assume that $\left|x_{in}\left(t\right)\right|\le M$.

In view of the definition for initialization function, we obtain:

$x_1\left(t\right)$ is decomposed into $x_1^{\left(1\right)}\left(t\right)$ and $x_1^{\left(2\right)}\left(t\right)$:

Next we prove the stability of $x_1^{\left(1\right)}\left(t\right)$ and $x_1^{\left(2\right)}\left(t\right)$ respectively:

In terms of Eqs. (12)-(14), we obtain that $x_1\left(t\right)\to 0$.

Our next target is to prove $x_2\left(t\right)\to 0$ as $t\to \mathrm{\infty }$.

We choose the Lyapunov function as:

where $z\left(\omega ,t\right)$ satisfies the following continuous frequency distributed model for the initialized fractional Caputo derivative ${}_0{}^{}{D}_t^{\alpha }{x}_2\left(t\right)$:

Differentiating $V\left(t\right)$, we obtain that:

We see that $\dot{V}\left(t\right)$ is semi-negative. Furthermore, letting $\dot{V}\left(t\right)=0$ we derive $z\left(\omega ,t\right)=0$. In terms of Eq. (15) and Eq. (10), we obtain ${\mathrm{}}_0{D}_t^{\alpha }{x}_2\left(t\right)=0$, ${\dot{x}}_2\left(t\right)=0$ and $x_2\left(t\right)=0$. As a result, the set of points where $\dot{V}\left(t\right)=0$ contains no trajectories other than the trivial one. By virtue of Lasalle’s theorem, the state ${\dot{x}}_2\left(t\right)$ is asymptotically stable.

From the above considerations, we come to the conclusion that $x_{zi}\left(t\right)\to 0$ as $t\to \mathrm{\infty }$. In other word, the initialization response of the fractional oscillator Eq. (1) is stable.

4. Conclusions

This paper has investigated the memory effects or historical effects on dynamical responses in fractional oscillators via numerical simulations. The stability of initialization response is proved on the basis of the unit impulse response function and the Lyapunov stability theorem. The main conclusion is that the stability of initialization response of fractional oscillators is irrelevant to initial conditions or prehistory.

The results in this paper have shown that the memory effects or historical effects on dynamics of viscoelastically damped structures should not be neglected. In engineering science and applications, the initialization function $\psi \left(t\right)$ which describes the effect of the past of fractional derivatives, should be taken into account and estimated to adequately predict the system response. For single-degree-of-freedom linear systems, the initial condition or prehistory has no impact on the dynamical stability of initialization response. However, situations for single-degree-of-freedom nonlinear systems and multi-degree-of-freedom systems are more intricate and should be investigated further. Moreover, historical effects on control design for fractional systems are also future efforts.