Bursting oscillation and bifurcation mechanism in fractional-order Brusselator with two different time scales

2.1. Bifurcation analysis

Letting $\theta =\omega t$, Eq. (2) can be converted into an autonomous form as:

Because the perturbation frequency is much less than the natural frequency of the original system, the reaction is a coupling system with two time scales. The fast subsystem (FS) is given by fast variable $x$ and $y$, while the slow subsystem (SS) is modeled by the slow process $\theta$. Based on slow-fast analysis, slow process can regulate the dynamical behaviors of the system, so the slow variable is usually regarded as the bifurcation parameter of fast subsystem. Defining $w=a\mathrm{c}\mathrm{o}\mathrm{s}\theta$, the FS can be written as:

which is the reaction process with constant forcing $w$.

By solving:

the equilibrium point of the FS Eq. (4) is obtained as:

The characteristic equation about the equilibrium point $E_0$ is:

If $1-B+(A+w{)}^2-2w/\left(A+w\right)>0$, the equilibrium point $E_0$ is stable. Accordingly, the necessary condition of Hopf bifurcation related to $E_0$ is $1-B+(A+w{)}^2-2w/(A+w)=0$.

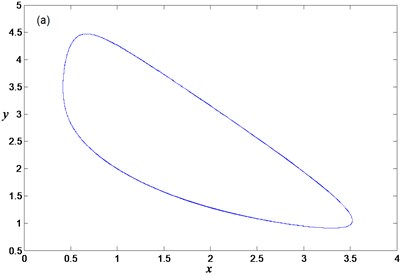
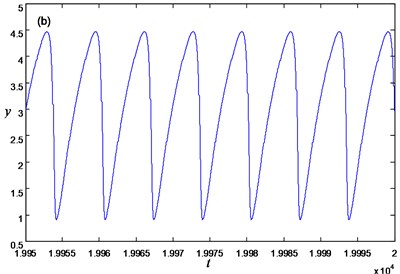
Considering the parameter $A=$ 1.06 and$B=$ 3, the bifurcation diagram of the FS with respect to slow variable parameter $w$ is plotted in Fig. 1, where the equilibrium curve $E-G$ is divided into four parts, i.e., stable focus located on $E-H1$, unstable focus denoted by dashed line on $H1-H2$, stable focus situated on $H2-F$, and stable nodes on $F-G$. $H1$ and $H2$ are the critical points of Hopf bifurcation, and the corresponding parameters are $w_{H1}=$ 0.5871 and $w_{H2}=$ –0.48165 respectively, which means stable limit cycles will appear in FS for –0.48165$<w<$ 0.5871. For example, Fig. 2(a) shows the phase portrait of periodic oscillation for $w=$ 0, and Fig. 2(b) is the time history of the FS.

Fig. 1Bifurcation diagram of the FS Eq. (4) with respect to parameter w

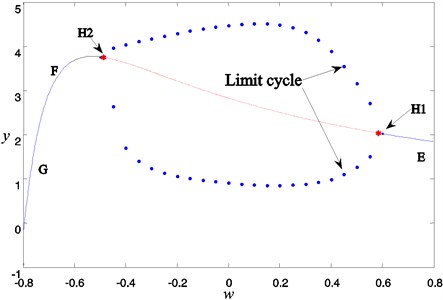
Fig. 2Limit cycle of the FS Eq. (4) for w=0: a) phase portrait, b) time history

2.2. Double-Hopf bursting oscillation and its bifurcation mechanism

Letting the frequency and amplitude of the external periodic perturbation as $\omega =$ 0.01 and $a=$ 0.7, one could obtain periodic bursting oscillation in system Eq. (2), and the phase portrait and time history are shown in Figs. 3(a) and 3(b) respectively. In each periodic oscillation, twice spiking and quiescent states exist. The frequency of the whole periodic oscillate is in accordance with perturbed frequency 0.01, while the oscillation in the spiking state may be coincide with the natural frequency of the FS Eq. (4) approximated as 0.94 (shown as Fig. 3(c)).

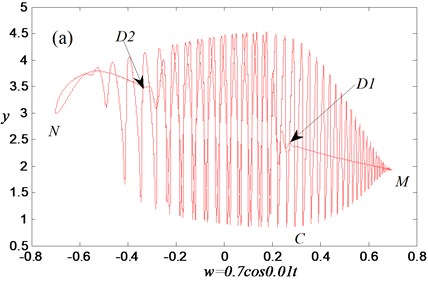
To further reveal the bifurcation mechanism of bursting oscillation, the transition portrait of periodic oscillation with respect to variable $y$ and slow process $w=0.7\mathrm{c}\mathrm{o}\mathrm{s}0.01t$ is shown in Fig. 4(a). Overlapping the transition portrait in Fig. 4(a) with the bifurcation diagram Fig. 1, one can obtain Fig. 4(b).

Now we can describe the evolution process of the periodic bursting oscillation in detail. Assuming that the trajectory starts from point C as shown in Fig. 4(b), one can see that the system Eq. (2) behaves with large-amplitude oscillation and is in the spiking state because of the attraction of the stable limit cycle of the FS Eq. (4). When Hopf bifurcation takes place at point $H1$, stable limit cycle disappears, and only stable focus exists in the FS Eq. (4), which leads to the oscillation amplitude decreasing gradually until the system settles down to the stable equilibrium curve. In other words, after $H1$ the spiking state gradually turns into the quiescent state with increase of $w$. When the trajectory gets to point $M$, slow variable $w=0.7\mathrm{c}\mathrm{o}\mathrm{s}0.01t$ reaches the maximum value, so that the trajectory may move with the decrease of $w$, and the system will remain the quiescent state. After passing through bifurcation point $H1$ again, the system appears gradually with small-amplitude oscillation. Along the equilibrium curve from point $D1$ to Hopf bifurcation point $H2$, the system is still in the spiking state. After that, the oscillation amplitude becomes smaller and smaller. When the stable limit cycle of the FS becomes a stable equilibrium point, the system enters the quiescent state. If $w$ approaching the minimum value, i.e. the trajectory reaches point $N$, the trajectory moves with the increase of $w$. Once again passing through the bifurcation point $H2$, the trajectory may be attracted by the stable limit cycle gradually. After passing through point $D2$, the system appears with large-amplitude oscillation and enters the spiking state again. In the whole process of the periodic bursting oscillation, it is related to two Hopf bifurcations of the FS, so that this oscillation is called as the double-Hopf periodic bursting oscillation.

Fig. 3Periodic bursting for a= 0.7: a) phase portrait, b) time history, c) partial enlargement of Fig. 3(b) in the spiking state

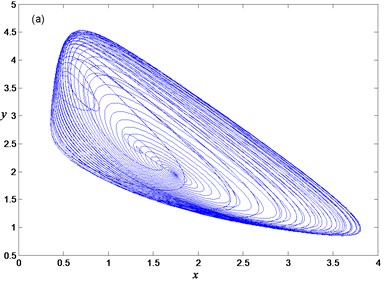
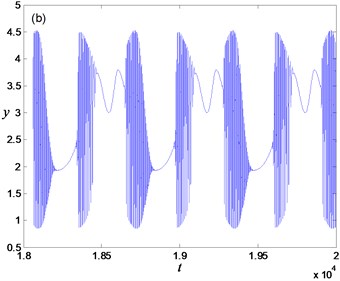
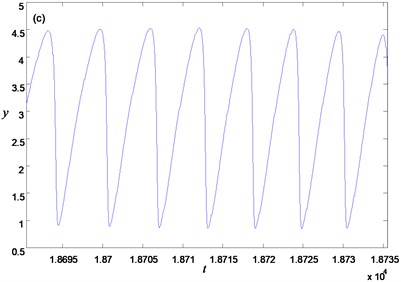
Fig. 4Mechanism analysis for bursting oscillation: a) transition portrait on woy, b) overlapping of transition portrait with bifurcation diagram

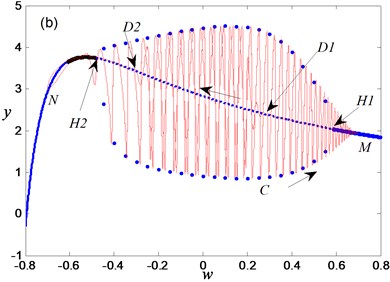
Here it should be pointed out that, the whole periodic oscillation has experienced four bifurcation processes although it involves two Hopf bifurcation points of the FS. In the vicinity of each bifurcation point, there is a transition from spiking state to quiescent state, and vice versa. It is the four bifurcation behaviors that makes the double-Hopf periodic bursting oscillation in the presence of two spiking and quiescent states. In addition, when spiking and quiescent states are transferred to each other, the time-delayed behaviors may occur in the system response due to the influence of inertia and other factors. For example, when the parameter $w$ decreases gradually through the bifurcation point $H1$, the system does not immediately appear large-amplitude oscillation. After some time, it will appear large-amplitude oscillation gradually and enter the spiking state. Similarly, when the parameter $w$ increases gradually through the bifurcation point $H2$, the system also appears a Hopf bifurcation delay [11, 36, 37].

2.3. Effects of external periodic perturbation amplitude on bursting oscillations

As the bifurcation diagram shown in Fig. 1, two Hopf bifurcations take place at $H1$ with $w_{H1}=\text{0.5871}$ and $H2$ with $w_{H2}=$ –0.48165 respectively, which indicates that the FS Eq. (4) may possess stable limit cycle attractors for $w_{H2}<w<w_{H1}$, or stable focus attractors for $w<w_{H2}$ and $w>w_{H1}$. Thus, the change of the perturbation amplitude will make the system involves different attractors of the FS Eq. (4).

When perturbation amplitude is $a>\text{0.5871}$, the range of parameter $w$ will contain the interval [–0.5871, 0.5871], so that the trajectory of the system Eq. (2) may involve three kinds of attractors, i.e. the stable limit cycle in the middle and the stable focuses on both sides. Bilateral bi-stability of the attractors results into the four times transformations of system Eq. (2) between spiking and quiescent states. Therefore, double-Hopf bursting oscillation may exist in system Eq. (2) with two spiking and quiescent states.

When perturbation amplitude $\text{0.48165}<a<$ 0.5871, the trajectory of the system only involves two kinds of attractors of FS Eq. (4), i.e. the stable focus on left side and the stable limit cycle in the middle. Accordingly, only unilateral bi-stability exists in the system, which means right bi-stability disappears and double-Hopf bursting oscillation will not occur. The time history diagram is shown in Fig. 5(a) for $a=\text{0.55}$. Compared with Fig. 3(b), it can be found that the disappearance of bi-stability on the right leads to the disappearance of the quiescent state on the right, which makes two spiking states be connected together and become into single spiking state. The single-Hopf bursting oscillation is determined by Hopf bifurcation on the left.

Fig. 5Time history diagram for: a) a= 0.55, b) a= 0.45

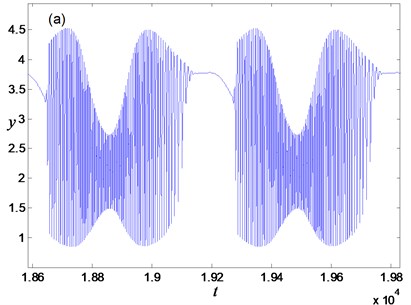
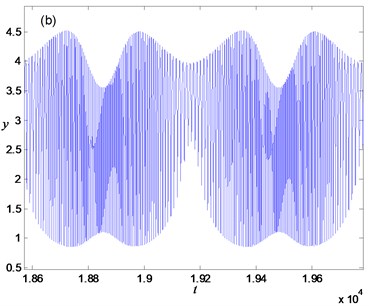
For perturbation amplitude $a<\text{0.48165}$, the trajectory only involves limit cycle attractors of FS Eq. (4), which leads the system Eq. (2) to keep in spiking state without quiescent state. For example, the quasi-periodic oscillation just with large-amplitude oscillation for $a=\text{0.45}$ is plotted in Fig. 5(b).

Therefore, when the slow process of a system with two time scales is forced by external periodic perturbation, the perturbation amplitude may adjust the oscillation patterns of the system. The mechanism is that the types of attractors involved in the FS will be changed if the perturbation amplitude varies.

3.1. Bifurcation analysis

Letting $\theta =\omega t$, Eq. (7) can be converted into an autonomous form:

If the perturbation frequency is much less than the natural frequency of the original system at least one order of magnitude, the reaction is a coupling system of two time scales. By defining $w=a\mathrm{c}\mathrm{o}\mathrm{s}\theta$, the FS can be written as:

For the abovementioned fixed parameter $A=\text{1.06}$ and $B=\text{3}$, the critical value of the stability region of the FS Eq. (9) will also be changed when the slow variable parameter $w$ varies. For the equilibrium point $E_0(A+w,(AB+wB+w)/(A+w{)}^2)$ of the FS Eq. (9), the corresponding characteristic equation reads ${\lambda }^2+(1-B+(A+w{)}^2-2w/(A+w))\lambda +(A+w{)}^2=0$.

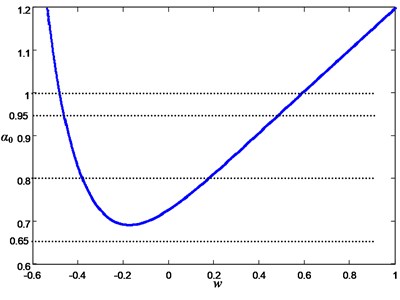
Combined Eq. (6), the double-parameter bifurcation diagram of FS Eq. (9) with respect to the parameters $w$ and the order ${\alpha }_0$ is plotted in Fig. 6. For $\text{0.69282}<\alpha <\text{2}$, two Hopf bifurcation points exist in the FS Eq. (9). With the decrease of $\alpha$, the distance between the two critical pints of Hopf bifurcation is getting smaller and smaller. In the end, the two points “collide” and disappear. For $0<\alpha <\text{0.6928}$, the Hopf bifurcation does not occur for the FS Eq. (9).

Fig. 6The bifurcation diagram of FS Eq. (9) with respect to parameters w and α0

3.2. Effects of fractional order on bursting oscillations

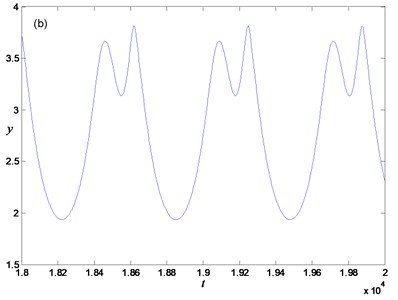
As shown in Fig. 6, there are two Hopf bifurcation points for $\text{0.69282}<\alpha <\text{2}$ in FS Eq. (9), and the Hopf bifurcation does not occur for $\text{0}<\alpha <\text{0.6928}$. For example, at $\alpha =\text{0.95}$, $I1$ and $I2$ are two Hopf bifurcation points, and the corresponding parameter values are $w_{I1}=\text{0.4844}$ and $w_{I2}=$ –0.4624 (see Fig. 7). Similar to the integer-order system, a periodic oscillation of the fractional-order system has still twice spiking and quiescent states. The difference is that as ${\alpha }_0$ becomes smaller, the distance between the two Hopf bifurcation points becomes much smaller, which leads to the time during the spiking state becomes much shorter, while the time during the quiescent state becomes much longer. When $\alpha =\text{0.65}$, the Hopf bifurcation point disappears. Although the system is still doing periodic motion, but there is no bursting phenomenon occurs (see Fig. 8). Therefore, the fractional order $\alpha$ plays an important role to control the bursting oscillation of the system.

For numerical simulations, the fractional-order differential system is different from integer-order one [38-41]. Here the Power Series Expansion method [23] is applied to compute the numerical solution of the fractional-order Brusselator. The phase portraits and time histories in Fig. 7 and Fig. 8 are plotted by MATLAB. Here the total computation time is 20000 s, and the step length is 0.001 s.

Fig. 7Periodic oscillation for α=0.95,a=0.7: a) phase portrait, b) time history, c) transition portrait on woy plane, d) overlapping of transition portrait with bifurcation diagram

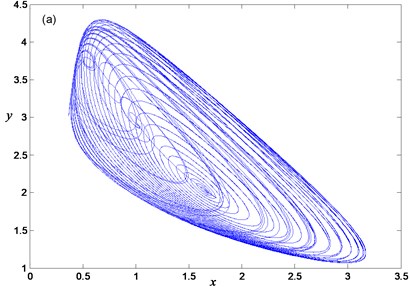
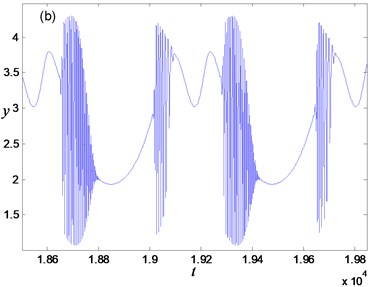
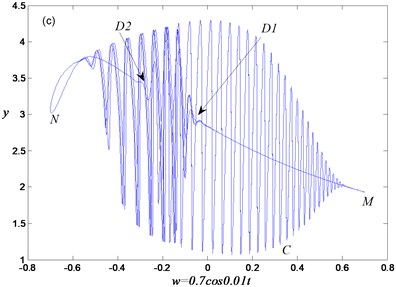
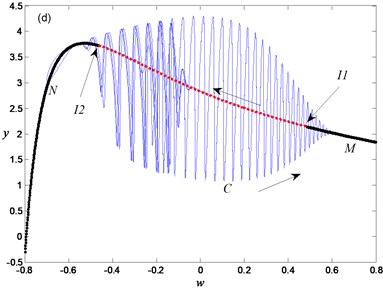
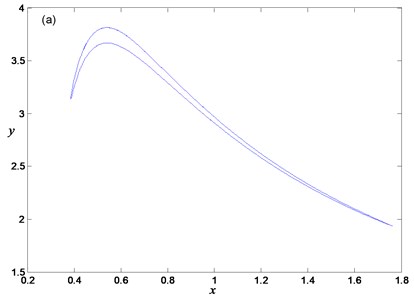
Fig. 8Periodic oscillation for α=0.65, a=0.7: a) phase portrait, b) time history