Dynamic analyses of osteoblast vibrational responses: a finite element viscoelastic model

1. Introduction

Mechanical stimuli always act on living cells of the human in whole life [1]. It is widely known that bone is a dynamic tissue, because the mechanical stimulus can control the bone resortion and/or apposition activities the bone remodelling cells and thus modify bone mass, shape and/or strength [2-5]. Since 1970 [6], many forms of mechanical stimuli have been used to analyse the biomechanic responses of bone cells in vitro, e.g. fluid shear stress [7], strain [8] and vibration [9]. While cells are complex systems, to investigate biological responses of cells under external mechanical stimuli, cells can be modelled as some simple models, e.g. linear elastic models [8, 10], viscoelastic models [11, 12], power-law structural damping model [13, 14], biphasic models [15, 16] and the tensegrity model [17, 18].

Finite element (FE) analysis is a very powerful and efficient research tool to simulate the responses of cells under the external dynamic mechanical stimuli [8, 19-21]. With the development of commercial FE analysis software, now it is possible to simulate the three-dimensional (3D) structure of cells. Shin and Athanasiou simulated the biphasic mechanical parameters of osteoblasts-like cells using the FE method [15]. McGarry and Prendergast developed a 3D FE model of an adherent eukaryoti cell [22]. Katzengold et al. simulated the large deformation behaviour for the maturing adipocytes using a 3D FE model [23]. To simulate the cellular mechanics behaviours like large deformation, the 3D cell-specific FE model was developed based on confocal microscopy [24]. In a recent study, to investigate viscoelastic property of bone cells under fluid flow, a new method was used combining fluid-structure interaction FE model and quasi-3D microscopy [12].

Some previous studies have obtained good achievements in studying viscoelastic material proteries of bone cells. For examples, elastic and viscoelastic tests were used to measure the biomechanical properties of individual cells (including spreading osteoblasts) using anatomic force microscope [25], and the viscoelastic material property of single adherent bone cells (osteocytes) was investigated by using a new non-invasive approach [12]. Furthermore, vibration analyses of the spreading bone cells (osteoblasts) were conducted using linear elastic FE continuum and tensegrity models to investigate vibrational characteristics of bone cells [26, 27]. However, the viscoelastic property was ignored in these studies [26, 27]. Since, it is well accepted that the viscoelastic property of cells play an important role in many biological and biophysical processes and responses [28-30], it is necessary to analyse the processes and mechanisms of vibrational responses of bone cells using the viscoelastic model.

In the current study, we aimed to analyse the biomechanical responses of osteoblasts to the external vibrational stimuli using a 3D FE viscoelastic model of osteoblasts. The main goals of this study were (1) to create the idealized continuum 3D FE models of osteoblasts; (2) to obtain natural frequencies and mode shapes of osteoblasts using the FE model; (3) to investigate the harmonic responses (like resonance frequency, displacement, strain and stress) to the different base excitation acceleration (i.e. 0.15$g$, 0.3$g$ and 0.5$g$) of the osteoblast FE model.

2. Materials and methods

2.1. Model geometry and FE modelling

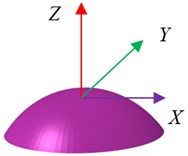
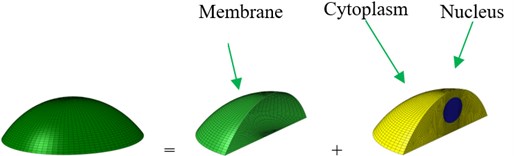
Based on the experimental investigation [31] and analytical model [22], the shape and geometry of an osteoblast are shown in Fig. 1. The osteoblast is comprised of three components, i.e. cell membrane, cytoplasm and nucleus. The idealized geometry of the osteoblast is a part of the sphere. The nucleus was always modelled as a sphere [32] or ellipsoid [22, 26, 27], and the shape of the nucleus was modelled as an ellipsoid in this study. Based on the investigation of McGarry and Prendergast [22], the volumes of the nucleus and whole cell were estimated as about 105 μm³ and 3000 μm³,respectively. Normally, the cell thickness was about 0.1-0.5 μm [32], and in this study the cell membrane was modelled as a shell with the thickness being about 6 nm [33, 34]. The cell height was about 2-20 μm [22, 34-36]. For an idealized model, the bottom surface of the cell can be an ellipse [26, 27, 37] or a circle [22, 35, 36, 38]. In this study, the microfilament and the microtubules were ignored. The dimensions of this model are given in Table 1.

Fig. 1Geometry and an idealized 3D finite element (FE) model of an osteoblast: a) geometry and b) whole FE modelling

a)

b)

Table 1Geometry property and element data for the osteoblast finite element modelling

Dimension					Number of elements
Cell height (μm)	Surface (μm2)	Bottom area (μm2)	Volume (μm3)	Nucleus volume (μm3)	Nucleus	Cytoplasm	Membrane
8.03	891.97	696.53	3010.90	104.72	23424	111808	10048

In this study, according to the corresponding geometry of the osteoblast, an idealized 3D FE model was developed (Fig. 1). ABAQUS 6.14 (SIMULIA, Providence, RI) was used to implement the FE analysis for the simulations. For the FE model, eight-node hexahedral elements (C3D8R for reducing the run time) were selected for the solid regions (including nucleus and cytoplasm). In addition, the cell membrane was meshed as the shell element S4R to save the run time. The FE element numbers of the nucleus, cytoplasm and membrane are presented in Table 1. To ensure a no-slip behaviour between nucleus-cytoplasm and cytoplasm-cell membrane, the tie constraint was used in this study.

2.2. Materials

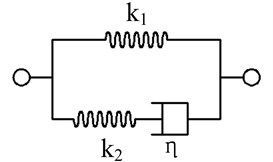
In this study, cell membrane and the nucleus were assumed as the linear isotropic elastic materials and cytoplasm was assumed as the linear viscoelastic material. The standard linear solid viscoelastic model (Zener model) can be described as Fig. 2.

Fig. 2A standard linear solid viscoelastic model

The extensional relaxation function is described [39]:

1

$E_R\left(t\right)=k_1+k_2{e}^{-t/{\tau }_R},{\tau }_R=\frac{\eta }{k_2},$

where $\eta$ is the damping coefficient (viscosity); $k_1$ and $k_2$ are spring stiffnesses (constants).

When $t=$0 and $t\to$∞, based on Eq. (1), the extensional relaxation function may be written as Eq. (2), respectively:

2

$E_R\left(t=0\right)=E_0=k_1+k_2,E_R\left(t\to \infty \right){=E}_{\infty }=k_1,$

where $E_0$ and $E_{\infty }$ are the instantaneous modulus and equilibrium modulus, respectively.

Based on Eq. (1b) and Eq. (2), the following equations can be obtained:

3

$k_2{=E}_{\infty }\frac{{\tau }_{\sigma }-{\tau }_R}{{\tau }_R},\eta {=E}_{\infty }\left({\tau }_{\sigma }-{\tau }_R\right),{\tau }_{\sigma }=\frac{\eta }{k_1{k}_2}\left(k_1+k_2\right).$

Normally, the prony series is applied to simulate the linear viscoleastic behaviour of bone cells including osteoblasts. The prony series can be expressed as [39]:

4

$G_R\left(t\right)=G_0\left[1-\sum _{i=1}^N{g}_i\left(1-e^{-t/{\tau }_i}\right)\right],G_0=\frac{3K(k_1+k_2)}{9K-(k_1+k_2)},$

where, $G_0$ is the instantaneous shear and bulk moduli (when $t=$0); $G_R\left(t\right)$ is the time-dependent shear relaxation modulus; $g_i$ and ${\tau }_i$ are the shear weighing factor (normally ranged between 0 and 1) and the relaxation time constant, respectively.

Based on the study of Qiu et al. [12], the viscoelastic parameters of the bone cell, $E_0$, $E_{\infty }$, and η were selected as 0.49±0.11 kPa, 0.31±0.044 kPa and 4.07±1.23 kPa, respectively. The elastic modulus of the membrane of the adherent eukaryotic cell was selected as 1 kPa [22, 40]. Young modulus ratio of cytoplasm and nucleus was chosen at 1:4 [22, 27, 41]. Moreover, Poisson’s ratios for membrane, cytoplasm and nucleus were assumed 0.3, 0.37 and 0.37, respectively in this study. The initial density of the cell was assumed as 1250 kg/m³ which was used as the density of cytoplasm [42], and the density ratio was assumed 0.4:1:1.2 to membrane, cytoplasm and nucleus [40]. Thus in this study, the densities of membrane, cytoplasm and nucleus of the osteoblast are 500 kg/m³, 1250 kg/m³ and 1500 kg/m³, respectively. The detailed material properties for the FE model are given in Table 2.

Table 2Material properties of the osteoblast finite element model

Material properties
Membrane	Cytoplasm	Nucleus
$E_0=$1.0 kPa, $\nu =$0.3, $\rho =$500 kg/m3	$E_0=$0.49 kPa, $E_{\infty }=$0.31 kPa, $\eta =$4.07 kPa s, $\nu =$0.37 and $\rho =$1250 kg/m3	$E_0=$1.96 kPa, $\nu =$0.37, $\rho =$1500 kg/m3

3. Results

3.1. Natural frequency extraction

The natural frequency (vibration resonant frequencies) and vibration mode shape of the FE model were obtained. The first ten natural frequencies are given in Table 3 and mode shapes of the first ten modes are presented in Fig. 3. To validate these results, the natural frequency from one previous study [27] is presented in Table 3 as well. Only the first five natural frequencies were given in the reference [27] and the frequency range was between 18.11 and 21.05 Hz. In addition, the range of the natural frequency was reported between 9.95-211.05 Hz for a spreading bone cell [26]. It can be seen that the varying trend and natural frequency values of the current study are in accordance with those of the previous study [26, 27].

Table 3Natural frequencies of the first ten modes of the finite element model (FEM) of an osteoblast

	1st	2nd	3rd	4th	5th	6th	7th	8th	9th	10th
FEM	19.99	20.01	24.09	30.12	30.15	30.48	31.97	31.98	34.43	34.48
Reference [27]	18.11	18.13	19.31	20.87	21.05
Difference %	9.40	9.40	19.84	30.71	30.18

From Fig. 3, it can be observed that the 1st and 2nd modes presented one direction oscillation, the 3rd and 6th modes showed the torsional modes, the 4th and 5th modes presented four oscillations, the 7th and 8th modes showed three oscillations, and the 9th and 10th modes showed two oscillations. These suggest that the shape and material properties of the bone cell may affect the natural frequency.

Fig. 3Mode shapes of the first ten vibration modes

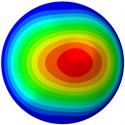
a) The 1st mode at 19.99 Hz

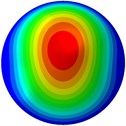
b) 2nd mode at 20.01 Hz

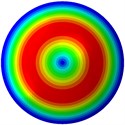
c) 3rd mode at 24.09 Hz

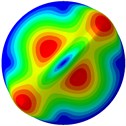
d) 4th mode at 30.12 Hz

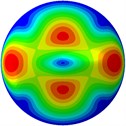
e) 5th mode at 30.15 Hz

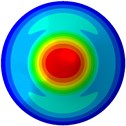
f) 6th mode at 30.48 Hz

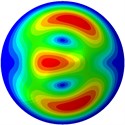
g) 7th mode at 31.97 Hz

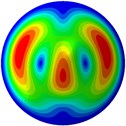
h) 8th mode at 31.98 Hz

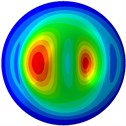
i) 9th mode at 34.43 Hz

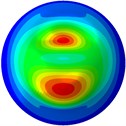
j) 10th mode at 34.48 Hz

Fig. 4The displacement of the centre of nucleus versus frequency

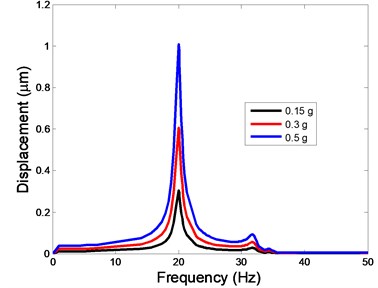
a)$X$-direction

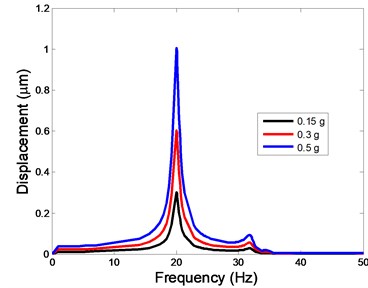
b)$Y$-direction

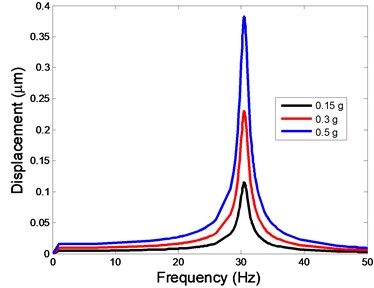
c)$Z$-direction

3.2. Harmonic vibration

As shown in Table 3, the lowest and highest natural frequencies are about 20 Hz and 34.48 Hz, respectively. Based on the natural frequencies and the assumed uniform acceleration of base excitation with the frequency range between 1 and 50 Hz, the harmonic responses of the viscoelastic FE model were computed for three different acceleration values, i.e. 0.15$g$, 0.3$g$ and 0.5$g$. The responses of displacement, strain and stress at the centre of the nucleus in the different directions ($X$, $Y$, $Z$-directions) to the harmonic vibration were investigated.

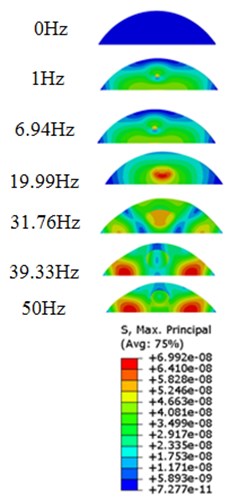
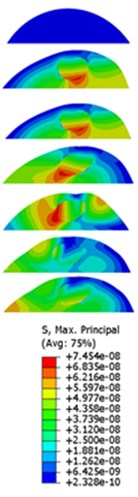
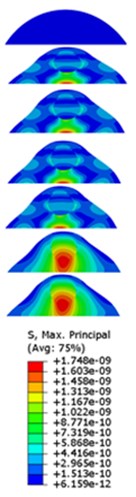
The displacement responses at the centre of nucleus are plotted as Fig. 4 for the different acceleration values of 0.15$g$, 0.3$g$ and 0.5$g$ and the different directions ($X$, $Y$, $Z$-directions). The mode shapes of the viscoelastic FE models under the 0.3$g$ base excitation at different frequencies (0, 6.937, 20.00, 30.01, 39.33 and 50 Hz) in $X$-direction, $Y$-direction and $Z$-direction are presented in Fig. 5.

Fig. 5Mode shapes at the different frequencies under the 0.3g acceleration

a)$X$-direction

b)$Y$-direction

c)$Z$-direction

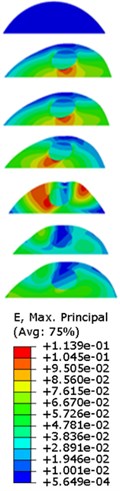
The strain responses at the centre of nucleus are plotted as Fig. 6 for the different acceleration values (0.15$g$, 0.3$g$ and 0.5$g$) and in the different directions ($X$, $Y$, $Z$-directions). The strain distributions of the FE models under the 0.3$g$ base excitation at different frequencies (0, 6.937, 20.00, 30.01, 39.33 and 50 Hz) in $X$-direction, $Y$-direction and $Z$-direction were also presented as Fig. 7.

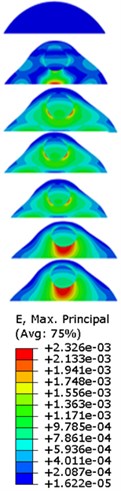
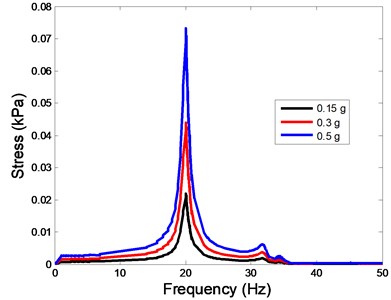
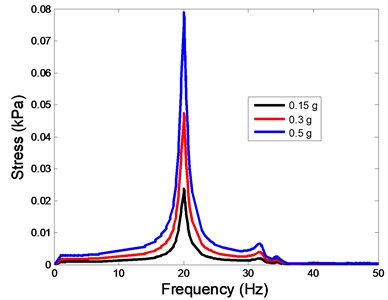
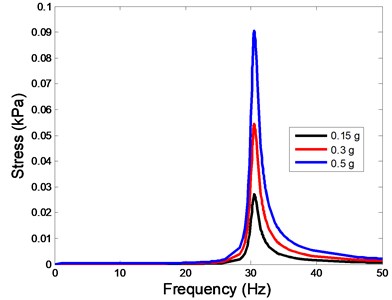
The stress responses at the centre of nucleus are plotted as Fig. 8 for the different acceleration values (0.15$g$, 0.3$g$ and 0.5$g$) and in different directions ($X$, $Y$, $Z$-directions). The stress distributions of the viscoelastic FE models under 0.3$g$ base excitation at different frequencies (0, 6.937, 20.00, 30.01, 39.33 and 50 Hz) in $X$-direction, $Y$-direction and $Z$-direction were also presented as Fig. 9.

4. Discussion

In this current study, a 3D idealized model was developed to investigate the vibrational responses of a spreading bone cell. Firstly, the natural frequency (resonance frequency) of the viscoelastic FE model was extracted. Then, harmonic vibration responses (displacement, stress and strain of centre of nucleus) of the viscoelastic FE models were analysed for the different base excitation acceleration values (0.15$g$, 0.3$g$ and 0.5$g$).

Fig. 6The strain values of the centre of nucleus versus frequency under the different acceleration values

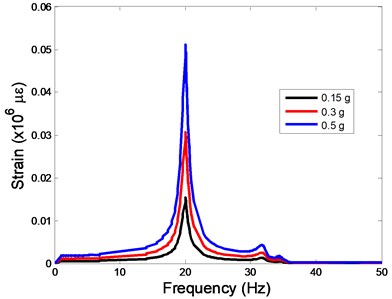
a)$X$-direction

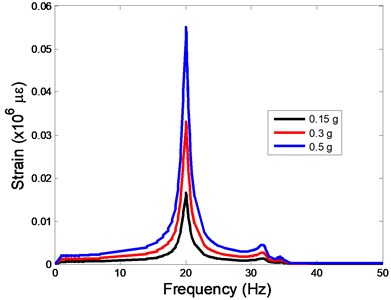
b)$Y$-direction

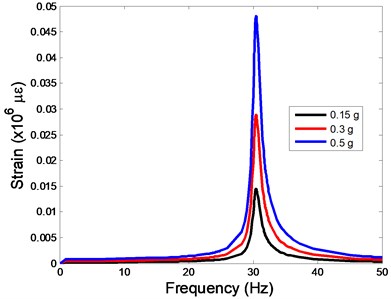
c)$Z$-direction

Fig. 7Strain contours of the cell under 0.3g acceleration for different frequencies and in X-direction, Y-direction and Z-direction

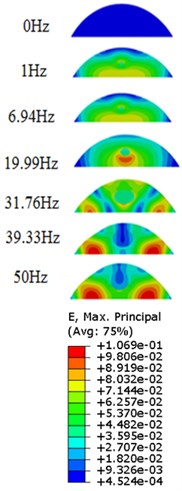
a)$X$-direction

b)$Y$-direction

c)$Z$-direction

The natural frequency of a bone cell (osteoblast) was predicted by using the viscoelastic FE model, with the first ten resonant frequencies of the cell being found between 19.99-34.48 Hz (Fig. 3). Based on the previous in vitro experimental studies, the vibration frequencies (5-100 Hz) were selected for the bone cell [9, 45]. The vibration frequency is important for bone cells to complete the bone bone formation and bone resorption [2, 46]. Similar natural frequency values were computed by other FE studies, e.g. the first ten natural frequencies an osteoblast were predicted as ~9.95-211.05 Hz [26] and as ~18.11-21.05 Hz [27]. Compared with the previours studies, it can be found that first ten natural frequencies from the current viscoelastic FE model are within the ranges from the literature. Therefore, the current viscoelastic FE model can be used to analyse the vibration behaviours of osteoblasts. In addition, it is noted that the natural frequencies are dependent on the material properties like density and geometry like the spreading shape.

Fig. 8The stress values of the centre of nucleus versus frequency under different acceleration values

a)$X$-direction

b)$Y$-direction

c)$Z$-direction

It is well known that the vibration responses depend on not only the excitation frequency but also how well the excitation conditions match the natural frequency and mode shape. For human activity, the acceleration is 1$g$, 3-4$g$ and 5$g$ for walking, running and jumping hurdles, respectively [47]. In another study, the acceleration of 0.04-19.3$g$ was used in a human vibration test, and the resonant frequencies were found to be 10-40 Hz, 10-25 Hz, 10-20 Hz and 10 Hz for ankle, knee, hip and spine, respectively [48]. In the current study, the one-degree-of –freedom vibrational system was applied, and the three different base excitation accelerations, 0.15$g$, 0.3$g$ and 0.5$g$, were used to investigate the effect of acceleration on the response of the bone cell. The results showed that the natural frequency does not change with the change of the base excitation acceleration, because the natural frequency of a bone cell is determined by the intrinsic factors of the cell (such as density) and is not affected by the external factors like loading.

In the present study, the displacement, strain and stress responses of an osteoblast were predicted by using the viscoelastic FE model under different accelerations. From Figs. 4, 6 and 8, it can be seen that the value of the displacement, strain and stress increase with the increasing acceleration. It also can be found that the values in $X$-direction are slightly smaller than those for the $Y$-direction, and the values in $X$-direction and $Y$-direction are larger than those of the $Z$-direction for the same acceleration in the three directions. In addition, the peak frequency values in $X$-direction and $Y$-direction are similar for the 1st vibration mode and $Z$-direction at 4th vibration mode. Wee and Voloshin [27] found that the resonance phenomenon of the bone cell in $X$-direction, $Y$-direction and Z-direction occurred at mode 1, mode 2 and mode 3, respectively. The resonance phenomenon of the bone cell depends on the geometry of the model.

Our FE analysis suggests that strain and stress are basically concentrated around the nucleus in $Z$-direction and move away from the centre of nucleus with the increasing frequency for the harmonic response under the 0.3$g$ acceleration (Figs. 7 and 9). It can be also revealed that the strain and stress distributions are different for the acceleration acting at $X$-direction, $Y$-direction and $Z$-direction due to the geometry and vibration direction.

Fig. 9Stress contours of the cell under 0.3g acceleration for different frequencies and in X-direction, Y-direction and Z-direction

a)$X$-direction

b)$Y$-direction

c)$Z$-direction

5. Conclusion

In the current study, a viscoelastic FE osteoblast model was developed, and the natural frequencies of the osteoblast FE model were extracted and the harmonic responses were analyzed under different acceleration values (0.15$g$, 0.3$g$ and 0.5$g$). It is found that the natural frequency range is between 19.99 and 34.48 Hz for the osteoblast FE model. The response values of displacement, strain and stress increase with the increase of base excitation acceleration. In addition, the response values in $Z$-direction are much bigger than those in the other directions ($X$, $Y$-direction) for the same base excitation acceleration. This osteoblast FE model could potentially be used to investigate cell deformation due to vibrational stimuli in vitro. It will help us to understand and guide the cell culture experiments in vitro.