Abstract
This work presents a novel dynamic modeling technique to predict the vibration of a pipe at different locations. An initial model of the pipe was constructed using experimental input-output data and system identification (SysID) techniques. The model derived through SysID showed a poor performance in predicting the vibration of the pipeline at locations other than that of the output sensor. Improvement of the SysID model was achieved using the Linear Quadratic Gaussian (LQG) observer-regulator modeling approach. While the hybrid model, combining both SysID and LQG, performed better, its transient response was not accurate. Further improvement to the model was achieved by incorporating a two degree of freedom, (2DOF) Proportional-Integral-Derivative (PID) to improve transient characteristics of the model. Experimental evaluation of the 2DOF PID assisted hybrid model showed good performance that far exceeded that of the hybrid model alone. The validity of the proposed approach was experimentally verified and the results are presented.
1. Introduction
Because of their easy integration in software and hardware, and because they are easy to design and tune, PID controllers are widely used in chemical process, electrical and dynamic systems [1, 2].
The performance of a controller is rated according to three criteria: load disturbance rejection, set-point response and robustness to model uncertainties in the process [3].
In conventional PID controllers, the disturbance response and set-point response influence each other making it impossible to properly tune both at the same time. On the other hand, 2DOF PID controllers do not suffer from such a limitation as disturbance rejection parameters and set-point response parameters can be adjusted separately. Araki and Taguchi [4] presented a survey of PID controllers performance which included equivalent transformations, described the effect of the 2DOF structure and proposed an optimal tuning method. Yukitomo, Shigemasa [5] introduced the Model-Driven TDOF PID control system, based on the Model-Driven control concept and used the quick responses for both set-point tracking and disturbance regulating response to show the effectiveness of the control system.
2. Improvement of the model
2.1. Construction of the hybrid model without 2DOF PID
In the experimental setup shown in Fig. 1 accelerometer (a) is located at the right end of the pipe section, accelerometer (b) is located in the middle of the section and accelerometer (c) is located at the left of the section. An instrumented hammer applies the excitation force at the right end of the pipe. DSpace and its data acquisition system measures the hammer force as well as the accelerometer responses.
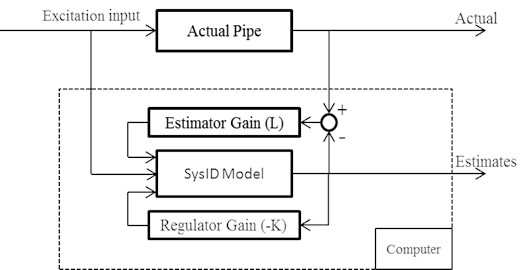
The experimental data is utilized in a hardware-in-the-loop format as shown in Fig. 2. to produce an optimal estimate of the pipe vibration at any desired location. It should be noted that only one accelerometer measurement is used to update the model (i.e., feedback signal), the remaining accelerometers are used for comparison with estimates at corresponding locations.
The system identification toolbox in MATLAB is utilized to obtain the initial model from raw experimental data [6, 7]. Moreover, the initial model is used to construct the hybrid model which uses the LQE and LQR techniques to generate optimal estimates of the system’s states such that the associated cost functions are minimized.
Fig. 1Experimental setup

Fig. 2Schematic of the hybrid model without 2DOF PID
2.2. Improving the model with 2DOF PID
A 2DOF PI controller is used to improve the performance of the hybrid model, the general block diagram of the PID control system [8] is shown in Fig. 3.
Fig. 3Block diagram of 2DOF control system
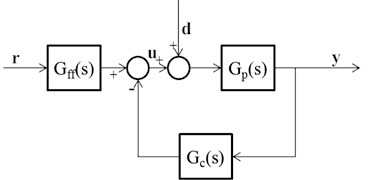
In the process,, and are transfer functions which are feedback and feedforward controllers as shown in Eqs. (1), (2) and (3):
Eq. (1) and (2) represent the PI controllers, in Eq. (2) the parameter has no influence on disturbance rejection, while it has a significant influence on the set point response. In Eq. (3) , and are the process gain, time constant and dead time, respectively.
Fig. 4Parameter setting panel of 2DOF PID
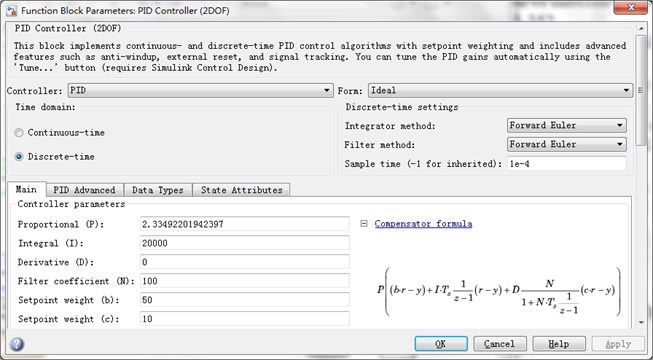
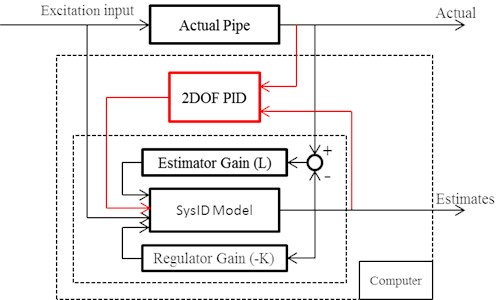
The parameter setting panel of 2DOF PID, in Simulink, is shown in Fig. 4. The parameter “Derivative (D)” is set to 0, to avoid adding any fictitious damping to the original model. Other parameters are properly adjusted to achieve proper tracking of the actual response of the pipeline at measurements location. The 2DOF controller is incorporated into the model as shown in Fig. 5. It is clear that the model uses feedback from the actual system to generate better estimates of the plant (actual pipe) states. The model produced can estimate, with good accuracy, the vibration at any location along the span of the pipeline without the need for any physical measurements at that location. This makes the proposed approach unique, as it uses minimal feedback measurements to yield good estimates at any desired location on the structure. This method can be used for any dynamic structure and it is not limited to pipelines only.
Fig. 5Schematic of improving the Hybrid Model with 2DOF PID
3. Simulation results
Comparison between the estimated response and the actual response using the hybrid model without 2DOF PID controller, in the frequency domain, is shown in Fig. 6 (the solid line represents the actual response and the dashed line represents the estimated one). It is clear that the model is capable of predicting the vibration fairly accurately with minimal discrepancies and exact resonant frequencies match. However, the amplitudes at each frequency are not accurate.
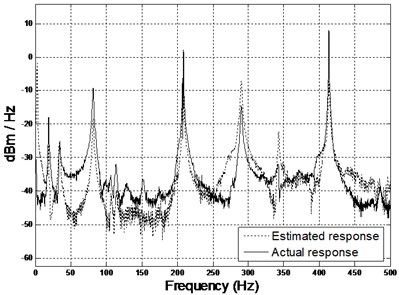
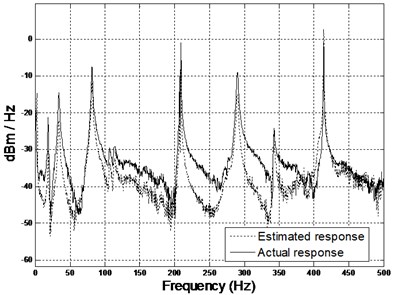
However, applying the 2DOF PID controller shows that the amplitude scaling has a significant improvement as shown in Fig. 7.
Fig. 6Comparison of spectrogram between estimated and actual results (middle and right accelerometers) using hybrid model
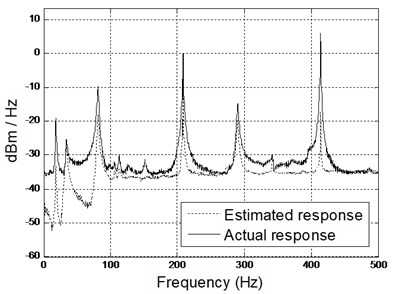
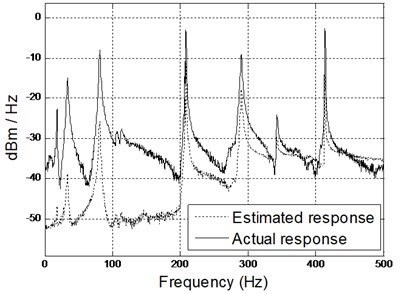
Fig. 7Comparison of spectrogram between estimated and actual results (middle and right accelerometers) using 2DOF PID
4. Conclusions
In this work, a novel approach for modeling a dynamic system using triple components is presented. An initial SysID model is constructed from impulse response data of the structure. After improvement of the initial model using LQE and LQR, combined LQG technique, it is further improved using a 2DOF PID controller. The latter improved the model significantly and its accuracy was verified experimentally. The model succeeded in predicting the vibration at any location of choice along a pipe with good accuracy.
References
-
Visioli A. Fuzzy logic based set-point weight tuning of PID controllers. IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, Vol. 29, Issue 6, 1999, p. 587-592.
-
Kim D. H. Tuning of 2-DOF PID controller by immune algorithm. Proceedings of the 2002 Congress on Evolutionary Computation, 2002.
-
Nemati H., Bagheri P. A new approach to tune the two-degree-of-freedom (2DOF). IEEE International Symposium on Computer-Aided Control System Design (CACSD), 2010.
-
Araki M., Taguchi H. Two-degree-of-freedom PID controllers. International Journal of Control, Automation, and Systems, Vol. 1, Issue 4, 2003, p. 401-411.
-
Yukitomo M., et al. A two degrees of freedom PID control system, its features and applications. 5th Asian Control Conference, 2004.
-
Ljung L. System Identification Toolbox: User’s Guide. Citeseer, 1995.
-
Ljung L. System Identification Toolbox for Use with MATLAB. 2007.
-
Åström K. J., Hägglund T. The future of PID control. Control Engineering Practice, Vol. 9, Issue 11, 2001, p. 1163-1175.
About this article
Authors acknowledge the support of the Petroleum Institute.
