Simulated identification on dynamic characteristics of large heavy-load bearing

1. Introduction

Nuclear energy is becoming one of the main new energies explored by countries in the world due to its economy and cleanness. China has been in the stage of fully developing nuclear power technology of kMW unit capacity, such as 1000 MW [1], 1550 MW [2] and 1750 MW [3]. As the promotion of unit capacity of nuclear generators, their bearings must be larger (diameter, over 800 mm) and heavier (specific pressure, $p_m$, over 3.3 MPa) [4, 5]. The dynamic characteristics of large heavy-load bearings (LHLBs) directly determine equipment’s operation quality. Obtaining the LHLBs’ dynamic characteristic coefficients is meaningful to assess stability and fault diagnosis of rotor-bearing system.

The high identification precision on bearing dynamic characteristic is difficult in the dynamics field for a long period. From the excitation mode, identification methods are divided into stable excitation method and instantaneous excitation method. The sine excitation is the most frequent stable excitation [6]. In addition, single-frequency twice excitation method [7], time domain least mean method [8], pulse excitation method [9, 10], unbalanced quality method [11, 12] and impulse response method [13] are available.

As for identification precision, a test of an ellipse bearing with diameter 32 in and $p_m$1.21 MPa was reported, and the stiffness coefficients difference of calculated value and identified value (DCI) is about 40 % [14]. For a five-pad tilting-pad journal bearing with diameter 116.8 mm and maximum $p_m$ 1.034 MPa, the DCIs of stiffness and damping coefficients are 10 %-30 % and 10 %-40 % respectively [15]. For a tilting-pad journal bearing with diameter 110 mm and $p_m$ 0.3 MPa, the DCIs of the main stiffness and main damping coefficients are about 25 %-55 % and 20 %-35 % respectively [16]. The effect of load direction on non-nominal five-pad tilting-pad journal bearings and identification of dynamic coefficients was studied [17]. Most references have researched the small light-load or moderate-load bearings, but the applicability of their identification methods to the LHLBs needs to be demonstrated. The new difficulties produced by large heavy-load still have no answers. For example, what is the proper value of dynamic force and response for the LHLBs? How will signal disturbance affect identification precision for the LHLBs?

Test rig is the basic tool of identification on dynamic characteristic coefficients. Generally, test rig in the lab has small size and small load, which is difficult to satisfy LHLBs’ test requirement. On the one hand, it’s very difficult and expensive to conduct the test of full-scale bearings. On the other hand, the test environment is complicated and it is difficult to separate single factor for influence analysis. The similarity theory of dynamic characteristics has not been formed. Compared to the real test, simulation test can freely select factors, precisely set their size, and be repeatedly conducted without consumption of plentiful resources.

This work aims to propose simulated test method of LHLBs’ dynamic characteristics and reveal effect rules of signal disturbance on identification precision. The features of LHLBs’ dynamic characteristic test is analyzed in Section 2. Section 3 establishes the identification model. Section 4 gives the calculating method of the positive and negative problems. Section 5 gives the results and discussion. Finally, conclusion is given in Section 6.

2. The features of identification on the LHLBs’ dynamic characteristic

The main parameters of case bearing are similar to them of the bearings used in the 1750 MW nuclear power generator which has the world’s largest unit capacity. The bearing’s dynamic characteristic coefficients under different $p_m$ are given in Table 2 by solving the hydrodynamics model.

The bearing performance is sensitive to the displacement disturbance under heavy-load as shown in Fig. 1. With increase of load, the sensitivity of liquid force to eccentricity continuously increases. The load is divided into light-load ($p_m\le$1.5 MPa), moderate-load (1.5 MPa $<p_m\le$3 MPa) and heavy- load ($p_m\ge$ 3 MPa) according to the current load of turbine or generator bearings. When displacement disturbance 10 μm occurs around eccentricity 0.44 mm ($p_m=$ 1 MPa), the change of $p_m$ is about 10.3 %. When displacement disturbance 10 μm occurs around eccentricity 0.54 mm ($p_m=$ 3.3 MPa), $p_m$ is over 4 MPa. At this time, the bearings dynamic characteristics have significantly changed. If the test values are compared with the original performance values, it will lead to tremendous error.

Fig. 1Liquid force of eccentricity (or specific pressures)

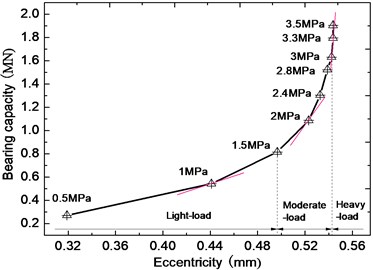
For the LHLBs’ dynamic characteristic test, what’s the proper displacement disturbance? 10 μm is required in dynamic characteristic test of general bearings [18]. The change of the main stiffness and main damping coefficients is about 40 % under disturbance 10 μm as shown in Table 3, and the maximum change of crossing coefficients reaches 71 %. Assuming that the permitted change of dynamic characteristic coefficients is less than 20 %, the permitted displacement disturbance should not be over 5 μm. The SNR will be very low in such small signal, so it proposes higher requirements for test precision [19]. At the same time, the rotation error and shape error of the rotating shaft should be considered.

3. Identification model

As shown in Fig. 2, the test bearing is suspended on the shaft and the excitation is directly imposed onto test bearing [20]. Because the disturbance factors of this test rig are relatively less, the identification model of LHLBs’ dynamic characteristic coefficients are established based on this test rig.

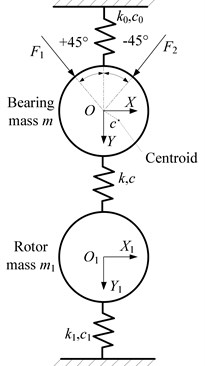
The linear assumption of liquid force is introduced firstly. Assuming that the dynamic load passes bearing’s geometric center and the bearing under plane motion, as shown in Figure 3, the dynamic equations of test bearing system are given as:

where $F_1$ and $F_2$ are dynamic load. ($X$, $Y$) is absolute displacement of test bearing to static balance position. ($X_1$, $Y_1$) is absolute displacement of shaft. ($X_2$, $Y_2$) is displacement of test bearing center to shaft center. $m$ and $m_1$ are mass of test bearing and shaft respectively. $k_0$ and $c_0$ are the connection stiffness and damping coefficients. $k_1$ and $c_1$ are the stiffness and damping coefficients of support bearing. $k$ and $c$ are the stiffness and damping coefficients matrix of test bearing.

Fig. 2Schematic diagram of the test rig 1 – shaft, 2 – support bearing 1, 3 – experiment module, 4 – chain, 5 – test bearing, 6 – bellows, 7 – support bearing 2, 8 – platform, 9 – damping base

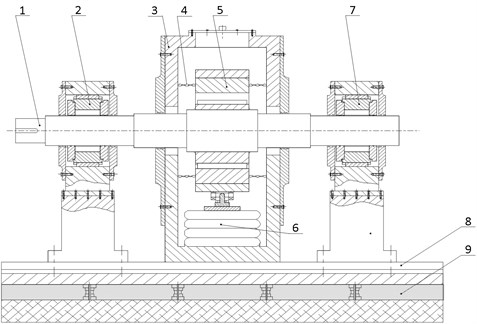
Fig. 3Dynamic model of test bearing system

Fourier transforming Eq. (1) to the equation of frequency-domain:

The dual-frequency excitation method, which means sine dynamic load in two directions and two frequencies (${\omega }_1$ and ${\omega }_2$) are simultaneously imposed onto test bearing. Displacement, mass, connection stiffness and damping coefficients are known, 8 linear equations can be established. $k$ and $c$ can be obtained by solving the equations.

4. Simulated test method

The simulated test is a process of combining solving the positive and negative problems. The positive problem means obtaining system responses based on load and system characteristics. The negative problem means identifying characteristic parameters based on load and responses.

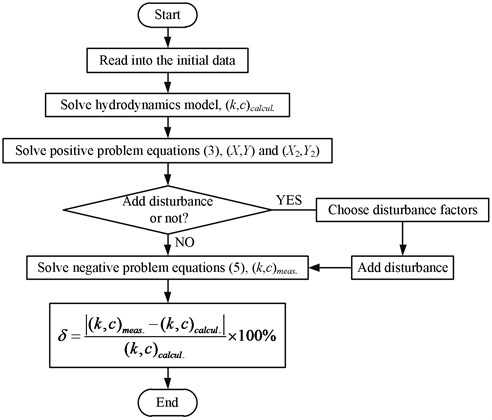
4.4. Flow of simulated test and accuracy assessment

Firstly, get theoretical values of bearing’s stiffness and damping coefficients ${\left(k,c\right)}_{calcul}$_. by solving the hydrodynamics model. Then solve the positive problem Eq. (3) to get response. Thirdly, add disturbances to force or displacement as shown in Eq. (7-12), and get identification values of bearing’s stiffness and damping coefficients ${\left(k,c\right)}_{meas.}$ by solving the negative problem Eq. (5). Compare the identification values with the theoretical values, and analyze the error at last. The flowchart of simulated test is shown in Fig. 4. Where $\delta$ is relative difference.

According to the calculation principle of positive and negative problems, if there is no error in calculation process, and no human interference, the identification results of dynamic coefficients should be completely equal in the given values. But in fact, decimals will be omitted in numerical calculation, which will result in a small difference. As shown in Table 4, identification error of the main stiffness and main damping coefficients is less than 0.25 %, and that of the cross term is less than 0.32 %. This shows that the matrix calculation accuracy is very high.

In addition, it’s important to analyze ill- condition of the test equations after giving values of the dynamic characteristic coefficients. Morbid recognition of Eqs. (6) is conducted to get the sensitivity of solution to disturbance of initial value. Condition number is used as an index to measure morbid degree. If condition number is relatively small, the equations is good. On the contrary, if condition number is relatively large, the equations is ill, and larger the condition number is, more serious ill condition is. In Eqs. (6), the 2 norm of the matrix $D$ and its condition number is 1.9×10^-4 and 41.1 respectively. According to the mathematical theory [21], condition number is less than 100, which indicates that Eq. (6) is in good condition.

Fig. 4The flowchart of simulated test

5. Results and discussion

5.1. Simulate test error with disturbance

5.1.1. Size and disturbance of dynamic load

Response is controlled by dynamic load directly, so the size of dynamic load needs to be restricted. $\gamma$ means the ratio of dynamic load amplitude to static load. In test of general bearing dynamic characteristic, $\gamma$ is 10 %-20 % [19]. Because the LHLBs’ permitted response is smaller, this paper guesses that $\gamma$ of the LHLBs may vary.

Taking a small ellipse bearing with diameter 100 mm for example, its gap ratio and $L/D$ ratio is same as them of the large one in Table 1. The relative displacement in vertical direction under different $\gamma$ can be obtained by solving positive problem equations, as shown in Fig. 5. For light load (1 MPa) and moderate-load (2.4 MPa), if the permitted response is 5 μm-10 μm, the permitted value of γ is about 17 %-34 %. For heavy-load (3.3 MPa), if the permitted response is 3 μm-5 μm, the permitted value of $\gamma$ is about 10 %-20 %. For the ellipse bearing with diameter 800 mm, if the permitted response under light load, moderate load and heavy load are 10 μm-15 μm, 5 μm-10 μm and 3 μm-5 μm, the permitted value of $\gamma$ are 5 %-8 %, 2 %-4 % and 1 %-2 % respectively. Compared to the light- load, $\gamma$ under heavy load is smaller and which will reduce with increase of bearing diameter.

The disturbance is added on amplitude and phase of dynamic load shown as Eq. (7). The disturbances of two excitation signals are identical. The crossing damping coefficients have small effect on dynamics computing of rotor-bearing system, so this paper will mainly discuss the main stiffness and main damping coefficients.

Fig. 5Displacement in vertical direction of different γ

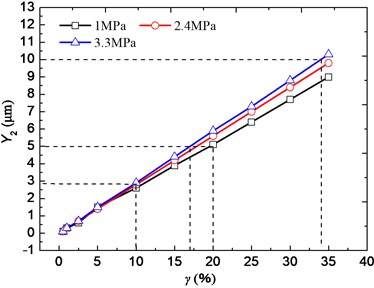
a) Diameter 100 mm

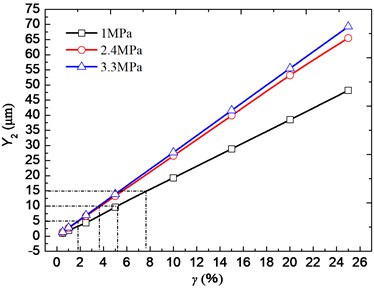
b) Diameter 800 mm

As shown in Table 4, with increase of amplitude disturbance, identification error of the stiffness and damping coefficients increases. Except crossing damping coefficients, the size of identification error keeps analogous with amplitude disturbance. If identification error of the main stiffness and main damping coefficients is less than 5 %, the amplitude disturbance of dynamic load should be less than 5 %. Phase disturbance has smaller effect on the stiffness coefficients and bigger effect on the damping coefficients. As for the LHLBs, if identification error of the main damping is less than 18 %, phase disturbance of dynamic load should be less than 1°. When the amplitude and phase disturbances coexist, the effect on identification precision will add linearly of effects under two separate disturbances.

Table 4Identification precision with disturbance of dynamic load changing

Amplitude disturbance (%)	Phase disturbance (°)	Relative error (%)
		$k_{xx}$	$k_{xy}$	$k_{yx}$	$k_{yy}$	$c_{xx}$	$c_{xy}$	$c_{yx}$	$c_{yy}$
0	0	0.07	0.23	0.19	0.19	0.09	0.15	0.32	0.25
3	0	2.70	2.76	3.39	3.76	3.32	3.39	5.09	4.38
5	0	4.65	4.64	5.38	5.75	5.50	5.40	8.19	6.77
10	0	9.52	9.32	10.34	10.73	10.97	10.43	15.95	12.75
0	1	0.44	0.53	0.42	0.68	13.03	7.22	48.17	18.27
0	2	0.68	1.04	0.40	0.55	25.99	14.84	95.85	35.72
0	3	0.96	1.57	0.35	0.40	38.90	22.48	143.45	53.12
3	1	2.48	2.27	3.40	3.66	16.70	4.43	54.26	22.39
5	1	4.42	4.13	5.39	5.65	19.15	2.57	58.32	25.13

5.1.2. Periodical disturbance of displacement

The periodical disturbance is added on absolute displacement and relative displacement simultaneously shown as Eq. (7). As shown in Table 6, assuming that identification error of the stiffness and main damping coefficients is less than 5 %, amplitude disturbance should be less than 5 %. And if identification error of the main damping coefficients is less than 10 %, phase disturbance should be less than 1°.

5.1.3. Random disturbance of displacement

The random disturbance is added on displacement shown as Eq. (8). As shown in Table 5, the effect of same disturbance on the damping coefficients is bigger than it on the stiffness coefficients, because although the random disturbance of displacement signals has limited effect on amplitude in frequency-domain, but it generates comparatively large effect on phase. Moreover, identification error of the stiffness and main damping coefficients in heavy-load is much bigger than it in light-load. If the disturbance value is 10 %, compared to $p_m$ 1 MPa, identification error of the main stiffness coefficients is 2-3 times bigger under $p_m$ 3.3 MPa, and the error difference of the main damping coefficients under two loads is about one order of magnitude. So, the random disturbance is the key factor in dynamic characteristic test of LHLBs and should be reduced in each step. For this case, if identification error of the main stiffness coefficients is less than 5 %, the random disturbance of displacement signals in time-domain should be less than 5 %.

Table 5Identification precision with periodical disturbance of displacement changing

Amplitude disturbance (%)	Phase disturbance (°)	Relative error (%)
		$k_{xx}$	$k_{xy}$	$k_{yx}$	$k_{yy}$	$c_{xx}$	$c_{xy}$	$c_{yx}$	$c_{yy}$
3	0	3.06	2.77	2.49	2.14	3.15	2.56	4.09	2.70
5	0	4.86	4.51	4.32	3.98	5.17	4.42	6.96	4.91
10	0	9.07	8.56	8.63	8.30	9.91	8.77	13.68	10.09
0	0.5	0.12	0.18	0.39	0.80	6.47	4.15	23.46	7.97
0	1	0.03	0.41	0.37	0.83	12.99	7.93	47.36	16.74
0	2	0.13	0.83	0.29	0.86	26.05	15.46	95.18	34.29
0	3	0.25	1.23	0.19	0.86	39.13	22.95	143.02	51.88
3	1	2.87	2.33	2.53	2.08	15.80	4.78	50.49	19.71
5	1	4.68	4.07	4.36	3.92	17.58	2.78	52.47	21.60
10	2	8.76	7.76	8.73	8.21	33.62	4.94	100.60	41.98

Table 6Identification precision with random disturbance of displacement under two loads

$p_m$ (MPa)	Disturbance (%)	Relative error (%)
		$k_{xx}$	$k_{xy}$	$k_{yx}$	$k_{yy}$	$c_{xx}$	$c_{xy}$	$c_{yx}$	$c_{yy}$
1	3	0.57	0.42	1.63	0.90	2.86	63.12	436.23	33.30
	5	0.81	0.94	2.34	3.31	9.42	95.63	804.59	26.31
	7	0.67	0.67	1.77	5.29	10.85	245.58	905.00	81.52
	10	2.88	2.03	9.01	8.23	5.94	94.07	780.12	27.42
3.3	3	2.42	8.73	3.48	3.11	54.66	67.58	175.51	62.48
	5	5.12	15.57	8.45	5.96	254.94	433.65	878.00	420.05
	7	5.84	33.33	10.40	15.47	113.83	258.33	411.20	255.05
	10	6.20	36.30	9.53	13.88	206.69	333.19	732.93	333.93

5.1.4. Roundness error and rotation error of large shaft

The simulated test results are shown in Table 7-Table 10. The values of rotation error and roundness error are obtained by using the circular graphical method [22]. For Table 7 and Table 8, compared to light-load, the same rotation error has bigger effect on identification precision under heavy-load. The identification error of the stiffness coefficients under heavy-load is about 25 times than it under light-load. The effect of the rotation error caused by the external excitation on the damping coefficients is much bigger than it on the stiffness coefficients. So, the rotation error caused by the external exception should be eliminated before solving Eq. (2) in LHLBs’ test.

Table 9 shows the effect of rotation error caused by self-excitation under heavy-load, and the effect is mutable. When the rotation error is less than about 11.74 μm, the effect on identification precision is less than 0.3 %. When it reaches 11.88 μm, the precision will suddenly deteriorate, which may be caused from resonance of the rotor system. The effect of the roundness error is similar as shown in Table 10. When the roundness error is at about 23.3 μm, the identification error will dramatically deteriorate. When diameter is 400-500 mm and grade of tolerance is 7, the roundness tolerance is 20 μm according to the standard. The roundness tolerance of case bearing with diameter 800 mm will exceed 20 μm, so its roundness error should be considered. For LHLBs, disturbance of large shaft should be eliminated by using multi-point method, multi-step method and so on [23].

Table 7Identification precision with rotation error caused by external exception (pm= 1 MPa)

$h_1$	$h_2$	Rotation error (μm)	Relative error (%)
			$k_{xx}$	$k_{xy}$	$k_{yx}$	$k_{yy}$	$c_{xx}$	$c_{xy}$	$c_{yx}$	$c_{yy}$
0	0	0	0.12	0.16	0.02	0.26	0.01	1.36	1.56	0.22
0.05	0.05	0.14	0.04	0.11	0.10	0.39	0.33	8.81	92.92	3.74
0.1	0.1	0.28	0.04	0.07	0.24	0.51	0.65	16.23	184.09	7.72
0.15	0.15	0.42	0.11	0.02	0.39	0.62	0.97	23.61	275.04	11.70
0.2	0.2	0.57	0.19	0.03	0.54	0.72	1.28	30.96	365.75	15.70

Table 8Identification precision with rotation error caused by external exception (pm= 3.3 MPa)

$h_1$	$h_2$	Rotation error (μm)	Relative error (%)
			$k_{xx}$	$k_{xy}$	$k_{yx}$	$k_{yy}$	$c_{xx}$	$c_{xy}$	$c_{yx}$	$c_{yy}$
0	0	0	0.22	0.05	0.41	0.77	0.04	0.37	0.43	0.79
0.05	0.05	0.14	0.51	0.00	1.30	0.22	44.50	57.78	179.29	65.98
0.1	0.1	0.28	1.50	1.91	3.58	1.43	86.99	114.25	349.04	130.04
0.15	0.15	0.42	2.83	5.33	6.55	3.38	126.46	167.96	505.72	190.60
0.2	0.2	0.57	4.45	10.04	10.06	5.93	162.28	217.91	646.87	246.57

Table 9Identification precision with rotation error caused by self-excitation (pm= 3.3 MPa)

$h_3$	Rotation error (μm)	Relative error (%)
		$k_{xx}$	$k_{xy}$	$k_{yx}$	$k_{yy}$	$c_{xx}$	$c_{xy}$	$c_{yx}$	$c_{yy}$
8.0	11.31	0.08	0.23	0.19	0.20	0.11	0.18	0.06	0.15
8.3	11.74	0.08	0.23	0.19	0.20	0.11	0.18	0.06	0.15
8.4	11.88	41.64	137.10	109.26	89.43	405.83	458.13	328.59	155.89
9.1	12.67	42.75	141.18	109.59	89.72	379.59	432.25	312.29	151.37

Table 10Identification precision with roundness error (pm= 3.3 MPa)

$A_r$	Roundness error (μm)	Relative error (%)
		$k_{xx}$	$k_{xy}$	$k_{yx}$	$k_{yy}$	$c_{xx}$	$c_{xy}$	$c_{yx}$	$c_{yy}$
0.5	2.0	0.08	0.24	0.19	0.20	0.02	0.07	0.46	0.04
5.0	15.9	0.09	0.34	0.17	0.22	0.66	0.74	7.51	2.56
8.0	22.0	0.10	0.40	0.16	0.23	1.11	1.27	12.20	4.25
8.7	23.3	26.93	81.29	109.87	90.17	892.90	944.30	160.49	107.73
9.0	23.9	27.62	83.80	110.08	90.35	877.95	929.61	151.19	105.15

6. Conclusions

As promotion of unit capacity of nuclear generators, their bearings are becoming larger and heavier, new difficulties to LHLBs’ dynamic characteristic test should be emphasized in the identification method and test system’s design. Simulated test on dynamic characteristics of the LHLBs is investigated in this work. Conclusions are as follows:

1) The diameter and load affect the permitted response and dynamic load. For large bearings with diameter 800 mm, if the permitted response under heavy-load is 3 μm–5 μm, the ratio of dynamic load and static load is 1 %–2 %, which is different from common knowledge of 15 %–20 % for small light-load bearings.

2) For the large bearing with $P_m$ 3.3 MPa, if identification error of the main stiffness and main damping coefficients is less than 5 %, the amplitude of periodical disturbance of dynamic load and displacement signals should be less than 5 %. If identification error of the main damping coefficients is less than 10 %, the phase of these two signals should be less than 1°. Identification precision of the damping coefficients is very sensitive to the random disturbance of signals.

3) Comparing to light-load, the same rotation error caused by external excitation has bigger effect on identification precision under heavy-load. The effect of rotation error caused by self-excitation and roundness error to identification precision has mutant character, and these errors of large shaft should be eliminated.