Abstract
Currently, multi-objective optimization of steering systems has seldom been reported, and this paper adopted GA-BPNN algorithm to optimize the top two order frequencies of steering systems. Firstly, this paper established the multi-body dynamics model of the steering system and obtained the random road spectrum of 4 wheels through mathematical model. Results showed that random road spectrums at different wheels were not totally the same and the position and size of peak values were also different. Therefore, the road spectrum of a wheel could not be used to replace the road spectrum of all wheels in multi-body dynamics simulation model. Otherwise, computational results would have a big error. Then, vibration accelerations of the steering wheel at different positions were extracted through the multi-body dynamics model of steering system. Results showed that there were two obvious peak values on the curve of vibration acceleration, and peak frequencies were 48.6 Hz and 65.1 Hz. The finite element model of steering system was established to compute the vibration acceleration, and it was compared with the experimental result. Relative error was controlled within 5 %. It indicated that the finite element model in this paper was reliable. In addition, the computational two order modal frequencies were completely the same with the peak frequencies of vibration acceleration, which proved that the peak values of vibration acceleration were totally caused by the top two order modals. Finally, GA-BPNN algorithm was proposed to optimize the structural thickness of key parts on the steering system, and the optimized result was then compared with that of BPNN and PSO-BPNN. Results showed that the optimization efficiency and result of GA-BPNN were obviously superior to those of other algorithms in the process of optimization and iteration. The optimized parameters were reapplied to the computational model of this paper. Vibration accelerations of the steering system at many positions were extracted to compare with those of the original result. Peak frequencies were significantly improved. In addition, vibration accelerations at most frequency points of the whole frequency band were significantly improved.
1. Introduction
The vibration of the steering system is an important factor affecting the NVH level of the whole vehicle and also has a direct influence on the handling stability, riding comfort and running speed. In addition, the driver directly contacts with the automobile steering system. Therefore, the design level of the steering system directly influences the subjective evaluation of users on vehicles. If the idle speed and shake of steering wheel during use is surely caused by the vibration of steering wheel after establishing the finite element model of steering system and conducting a preliminary analysis, it is necessary to appropriately improve the resonance modal frequency of steering system.
At present, studies on steering system have obtained many achievements. Kim [1] found main influence factors for the vibration of steering wheel through studying the heterogeneity of tires, tire pressure and the exciting force of road surface. Yu [2, 3] analyzed the impact of brake torque fluctuation and transfer sensitivity of chassis vibration on the vibration of steering wheel, verified the analyzed result in frequency domain and time domain, and provided a very good method for analyzing the vibration of steering wheel. The high-speed shake and its influence factors of steering wheel have already been proposed by researchers. References [4, 5] analyzed and optimized the shake of steering wheel of a vehicle running at a high speed through experiments. However, the experimental process was very complicated and time-consuming, which increased the development cost of whole vehicles. Park [6] and Kim [7] decomposed the modal frequency of steering system into steering support and the modal frequency of steering column, studied main structural parameters affecting steering support and the stiffness of steering column and gave design regulations to control the modal frequency of steering system. Reference [8] adopted finite element method to analyze the sensitivity of NVH of dash panel and steering system to the thickness of machine parts. Based on the dynamic model of suspension and steering system, reference [9] adopted an optimization algorithm based on simulated annealing to improve the handling stability of the vehicle. Reference [10] replaced finite element model with response surface technology and optimized the first order natural frequency of steering system.
Finite element method [11] was mostly adopted in the reported papers to analyze and optimize steering system mainly because of high accuracy and efficiency of finite element method. To better solve various problems of performance optimization in engineering, some scholars have proposed to replace finite element method with relatively simple approximation model, effectively avoiding the invisibility of finite element in the computational process and shortening computational time. However, different approximation model technologies are faced with limitations though they have unique advantages in respective fields. It is because approximation model is difficult to express the detailed features of steering system. Its correctness of predicted result remains to be verified.
Currently, steering system has seldom been optimized and analyzed in published reports. In addition, optimization objective is mostly the first order natural frequency of steering system. However, engineering research results show that the vibration of steering system is not only affected by the first order modal frequency and the second order modal frequency in steering system cannot be neglected. Therefore, this paper considered using GA-BPNN algorithm to conduct objective optimization for two order modal frequencies of steering system and obtained a structure with optimal performance.
2. Multi-body dynamics model of steering system
2.1. Establishment of multi-body dynamics model
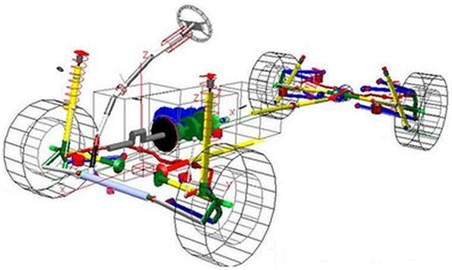
Some detailed parts needed to be simplified when steering system of a vehicle is established. After simplification, the steering system was composed of steering wheel, steering column, steering shaft, steering rack and steering tie rod. The first step was to choose a good coordinate system. For the convenience of modeling, the opposite direction of the running vehicle was taken as the positive direction of -axis; the right direction of the vehicle was the positive direction of -axis; the direction perpendicular to the ground was the positive direction of -axis. The establishment of steering system model would neglect internal clearance and friction between kinematic pairs and regard each kinematic pair as rigid connection. According to the key point coordinate of steering system, ADAMS was used to establish the model of steering system, as shown in Fig. 1.
2.2. Random road spectrum
Only the multi-body dynamics model of steering system was established above. However, the road spectrum which should be consistent with actual road conditions still needed to be constructed in order to simulate the actual driving process of the vehicle. The construction of random road spectrum which met certain regulations of random distribution and the requirements of tire model in ADAMS software was a key step to the random road surface simulation work of the vehicle. However, different levels of random road surfaces could not be directly generated in ADAMS/Car. As a result, random road surfaces needed to be obtained through establishing mathematical model.
Fig. 1Multi-body dynamics model of steering system of a vehicle
This paper used the basic principle of sine wave superposition method to generate a random road surface spectrum. The power spectrum density of road surface used the following formula for fitting:
where, was space displacement power spectrum density of road surface; referred to spatial frequency which was the function of wavelength and stood for the number of wavelengths in each meter; represented reference spatial frequency, ; was the road surface spectrum value under reference spatial frequency ; was frequency index and frequency index in graded road surface spectrum.
was the power spectrum density of road surface roughness in spatial frequency . Through using the nature of spreading frequency spectrum in stationary random process, the variance of road surface roughness could be expressed in the following form:
In the integral operation of Eq. (2), the range of spatial frequency could be divided into small intervals. The width of each small interval was . Power spectrum density value of road surface roughness at the center frequency of each small interval was used to replace the value of in the whole spatial frequency . Eq. (2) could be expressed in the following form:
To obtain random road surface roughness, spatial frequency and standard deviation could be applied to obtain sine wave function to show road surface model. Sine wave function could be expressed in the following form:
The superposition of sine wave functions in each corresponding internal could obtain random road surface roughness model as follows:
Different road surface levels of random road spectrums could be obtained according to Eq. (5). Fig. 2 presented B-grade road spectrums obtained through adopting the above equation.
Fig. 2Random road spectrums of simulation model
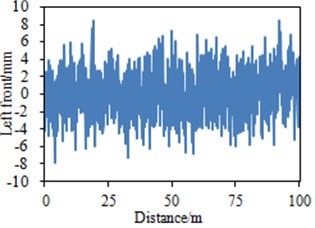
a) Left front wheel
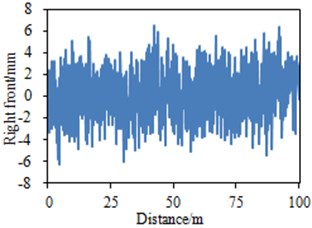
b) Right front wheel
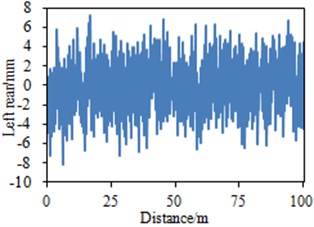
c) Left rear wheel
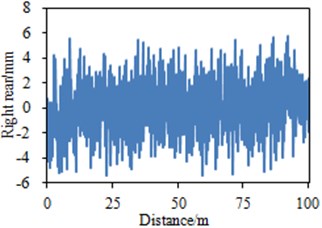
b) Right rear wheel
It could be seen from Fig. 2 that road spectrums at four vehicle wheels of the vehicle were not completely the same and fluctuated around 0. The maximum and minimum values of random road spectrum of the left front wheel were 8.3 mm and –8 mm; the maximum and minimum values of road spectrum of the right front wheel were 6.4 mm and –6.2 mm; the maximum and minimum values of road spectrum of the left rear wheel were 7.2 mm and –8 mm; the maximum and minimum values of road spectrum of the right rear wheel were 5.9 mm and –5.6 mm. In addition, the maximum and minimum values of road spectrums of four vehicle wheels were at different positions. Therefore, the road spectrum of a vehicle wheel could not be used to replace the road spectrum of all wheels in multi-body dynamics model. Otherwise, computational results would have a big error. The road spectrums were inputted into multi-body dynamics model in Fig. 1 to extract the vibration acceleration of steering wheel at two different positions, as shown in Fig. 3.
Vibration accelerations of the steering wheel only within 200 Hz were extracted to conduct an analysis. The frequency band mainly included mechanical vibration and the shake of steering wheel usually was in the frequency band. As displayed from Fig. 3, vibration accelerations at two positions of the steering wheel had obvious peak values at the frequency of 48.6 Hz and 65.1 Hz. At other frequency points, vibration accelerations of the steering wheel showed no obvious peak values. The first and second peak vibration accelerations were 0.89 m/s2 and 0.65 m/s2 at point 1 of steering wheel; the first and second peak vibration accelerations were 0.85 m/s2 and 0.62 m/s2 at point 2 of steering wheel. Obvious peak vibration accelerations were the primary cause of shake of steering wheel. As a result, it was necessary to adopt some measures to reduce acceleration peak values and improve peak frequency.
Fig. 3Vibration acceleration at different positions of steering wheel
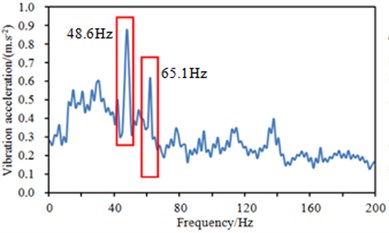
a) Point 1
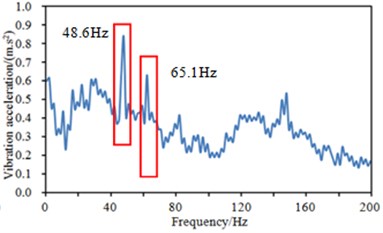
b) Point 2
3. Finite element model and experimental verification of steering system
3.1. Finite element model of steering system
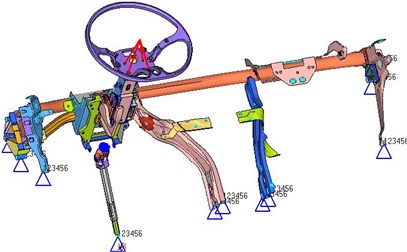
According to the above analysis, the steering system had two order resonance frequencies. Thus, resonance could be avoided through improving the structure of steering system. Fig. 4 displayed the geometric model of steering system and position of applying constraints.
Fig. 4Geometric model of steering system
The mesh of steering system was divided, including 65453 nodes and 75349 elements. There were 64585 shell elements, 10764 tetrahedral elements. The rest contained Rbe2 and spring elements. The connection of spherical hinges used Rbe2 for simulation. Corresponding degrees of freedom were released according to the actual situation. Rubber bushings of main parts were simulated by spring. Tetrahedral elements were applied to simulate solid parts including steering wheel and steering knuckle involved in the model. Plate and shell parts like IP cylindrical beams were simulated by mixed elements mainly including quadrangle. Parts connecting with the vehicle body in the model constrained degree of freedom in 6 directions. Mass constraints were applied above the steering wheel to simulate the added mass of steering wheel. The steering wheel was made of steel. Therefore, elasticity modulus was 2.1e11 Pa; density was 7800 kg/m3; Poisson’s ratio was 0.3. Finally, the finite element model of steering system was obtained, as shown in Fig. 5. The first two order constraint modals of steering system could be calculated through the finite element model.
Fig. 5Finite element model of steering system

3.2. Experimental verification of finite element model
As shown in Fig. 5, the constraint conditions and connection among structural parts of the finite element model were very complicated. As a result, it was necessary to experimentally verify the modal of finite element model of steering system. Otherwise, the reliability of computational results and model could not be guaranteed. Modal experiment adopted the vibration noise test system produced by B&K. The system contained two parts, namely hardware and software. Hardware equipment used in the test included multi-channel data acquisition system, force hammer, acceleration sensor and so on. Testing the modal of steering system involved establishing the geometric model of steering system, defining the degree of freedom and determining the direction of measurement in pulse modal test system. The force hammer could be used to quickly master the method of modal test and gain rich experience of modal test. Regarding documents obtained after modal test, special analysis software was required to conduct fitting for data and estimate the modal parameters of system. Equipment used in modal test was shown in Fig. 6. Each test point was hammered three times. The average value of three experiments was taken as the final result.
Fig. 6Test equipment and position of steering system modal

a) Multi-channel data acquisition equipment

b) Force hammer

c) Position of acceleration sensor

d) Acceleration sensor
The computational modal by finite element model was compared with that of experiments. The result was shown in Table 1. As displayed from Table 1, the relative error of experimental and simulation modal was controlled within 5 %, which indicated that finite element model was effective. In addition, the numerical value of experimental and simulation modal was just consistent with the peak frequency of vibration acceleration in Fig. 3, which showed that the top two peak vibration accelerations of steering system were mainly caused by the top two modals of steering wheel. Therefore, some measures would be subsequently taken to raise the two modal frequencies and improve the vibration characteristics of steering system.
The top two order modes of steering system were extracted, as shown in Fig. 7. As displayed from Fig. 7, the relatively severe vibration of steering system mainly appeared in steering wheel and its connection parts. In actual engineering, casting grinding tools would be changed and cost would be increased through changing the structural form of parts of steering system. Therefore, this paper only considered changing the thickness of these parts to study the vibration characteristics of steering system.
Table 1A comparison of experiment and simulation of the top two modals of steering system
Number of order | Mode of vibration | Computational result / Hz | Experimental result / Hz | Relative error / % |
1 | Pitching motion of steering wheel | 48.6 | 47.5 | 2.3 |
2 | Left and right motion of steering wheel | 65.1 | 64.4 | 1.2 |
Fig. 7The top two order modes of steering system
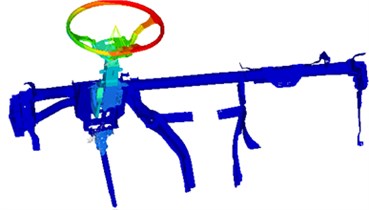
a) 48.6 Hz

b) 65.1 Hz
4. Optimization of vibration characteristics of steering system
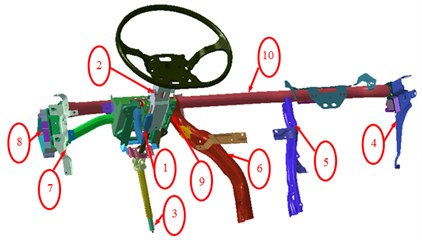
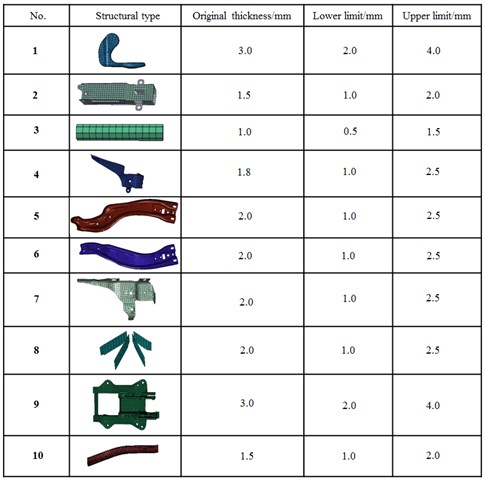
Parts concerned in the steering system were numbered, as shown in Fig. 8. These parts were mainly connection parts between steering system and the vehicle, and support parts of the steering wheel. These parts were taken as design variables to optimize the vibration performance of steering system. The size and upper and lower limits of variables were shown in Fig. 9.
Fig. 8Key parts of steering system
BP neural network is error back propagation neural network. It is a network composed of nonlinear transformation units. Its essence is to solve the minimum value of error functions. In recent years, BP neural network has been widely applied in optimization and analysis due to its simple structure, many adjustable parameters and training algorithms and good operability. However, BP neural network is limited in multi-objective optimization due to its defects including slow learning convergence speed, inability of guaranteeing to converge to local minimum and difficulty in accurately gaining network structure, initial weights and thresholds of network significantly affecting network training. Under normal circumstances, the above problems can be solved with the method of intelligent optimization. After these defects are eliminated, the strong autonomous learning ability and superior predictive ability of BP neural network are able to be effectively applied in the multi-objective optimization of finite element model. Optimization algorithm is used to optimize neural network in two aspects. Firstly, network structure is optimized, namely determining the number of hidden layers and the number of nodes in each hidden layer. Secondly, initial weights and thresholds of network are optimized. Three layers of BP neural network have been enough to solve most problems. Too many hidden layers cannot greatly improve computational accuracy, but spend more computing time. This paper introduced genetic algorithm to optimize the initial weights and thresholds of BP neural network and constructed an improved BP neural network based on genetic algorithm.
Fig. 9Size and upper and lower limits of optimized variables of steering system
It could be seen from the above analysis that the vibration acceleration peak value of steering system was mainly determined by the top two order vibration frequencies. Therefore, the optimization problem of steering system studied in this paper was obviously multi-objective optimization problem [12-15]. It was supposed to adopt multi-objective optimization algorithm for an optimized solution. The improved BP neural network based on genetic algorithm [16-22] possessed obvious advantages in multi-objective optimization. The constructed genetic algorithm was used to optimize BP neural network in the following steps:
1) Generated the initial weights and thresholds of BP neural network at random and adopted the method of binary encoding to generate chromosomes . Each individual was composed of four parts, including connection weights of the input layer and hidden layer, thresholds of the hidden layer, connection weights of the hidden layer and the output layer as well as thresholds of the output layer.
2) Chose the error matrix of predicted value and expected value of neural network samples as the output of objective function.
3) Selected and used random traversal sampling operators for crossover, chose simple single point crossover operators as crossover operators, took 0.01 as mutation probability and adopted the random method to pick out mutated genes.
4) Went back to the first step if obtained weights and thresholds of neural network failed to satisfy error requirements.
5) The newly obtained BP neural network would be trained if obtained weights and thresholds of BP neural network satisfied error requirements. The eigenvalue vector of finite element model was considered as input to obtain optimized parameters.
6) Optimized parameters were inputted into finite element model. It was supposed to modify the range of initial weights and thresholds and go back to the first step if obtained analysis frequency failed to satisfy the requirements of accuracy. The optimization of finite element model was finished when optimized parameters satisfied the requirements of accuracy.
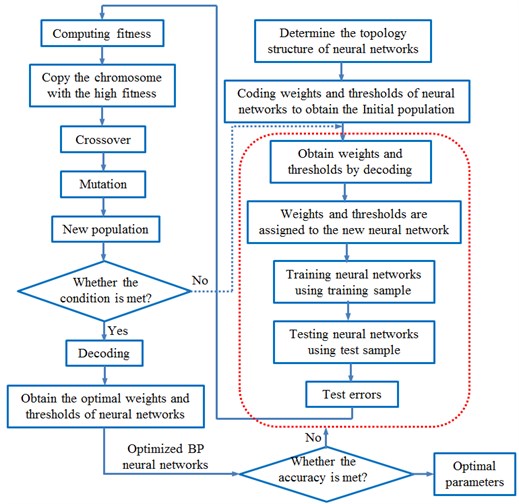
Based on the above analysis, detailed optimization process was made, as shown in Fig. 10.
Fig. 10Process of optimizing BP neural network through genetic algorithm
The design variable of this paper was the thickness of main plates. In the finite element model, these plates had shell elements and solid elements. It was rather difficult to optimize the thickness of solid elements. To solve this problem, this paper rebuilt shell elements on the surface of entity components to ensure the superposition between the nodes of shell elements and solid surfaces. The thickness of solid structures could be indirectly optimized through optimizing the thickness of shell elements. The original thickness and designed upper and lower limits of each plate were shown in Fig. 9. Two order modal frequencies of steering wheel of automobile running at a high speed were taken as the objective function, set as . The mass of steering system was considered as the constraint function, set as . The thickness of various parts was regarded as design variable. Its mathematical model was shown below:
where in, was the first order modal frequency of steering system; represented the second order modal frequency of steering system; was design variable; the original mass of steering system was 12.5 kg; stood for the lower limit of design variable; was the upper limit of design variable.
Through compiling the interface program of MATLAB and ANSYS, GA-BPNN could be quickly applied to optimize the modal frequency of steering system. To equally consider various optimization parameters and avoid the unstable weights and thresholds of BP neural network obtained by optimization, the numerical value of parameters to be optimized was taken as output after normalization processing. BP neural network was trained after obtaining weights and thresholds of BP neural network optimized by genetic algorithm. According to the result obtained by test samples, the error of optimizing BP neural network algorithm with the optimal weights and thresholds obtained after 100 generations of genetic optimization reduced below 0.1 %, which satisfied the requirements of accuracy. The multi-objective optimization of steering system was conducted according to the above optimization process. Genetic algorithm parameters required by optimization were set as follows. The number of population was 60; the number of iterations was 30; crossover probability was 0.8; mutation probability was 0.2. To further verify the effectiveness of GA-BPNN after parameter selection, GA-BPNN was compared with BP neural network model (BPNN) and particle swarm optimization neural network model (PSO-BPNN). BPNN, PSO-BPNN and GA-BPNN adopted the same neural network topology to conduct multi-objective optimization for the modal frequency of steering system. The training error of three kinds of optimization algorithms was shown in Fig. 11.
Fig. 11A comparison of training errors of three kinds of algorithms
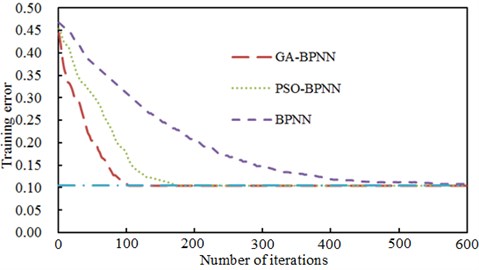
The condition of terminating neural network training process adopted the largest number of iterations and thresholds of training error. As displayed from Fig. 8, the error convergence values of BP neural network, genetic neural network and particle swarm neural network were 0.320, 0.187 and 0.099 when the number of their iterations was 100. Only the training error value of GA-BPNN was less than the error threshold, namely 0.1. In addition, BP neural network converged to the threshold 0.1 when the number of iterations was 600. Therefore, GA-BPNN algorithm showed better training features in the training process of neural network. To avoid randomness, training was repeated 50 times to obtain the average training result of 3 kinds of neural network models, as shown in Table 2. It could be noticed from Table 2 that the first order modal frequency value obtained by using GA-BPNN was larger than that obtained by using other algorithms. It verified the effectiveness of GA-BPNN algorithm in the multi-objective optimization of steering system.
To present the iteration process of three algorithms more vividly, two order modal frequencies were taken as vertical and horizontal coordinates to obtain the population figure of steering system. The result was shown in Fig. 12. As displayed from Fig. 12, the performance of most individuals was superior to that of original individuals in the process of optimization. The whole population showed a high evolutionary level. However, the large number of iterations was reflected in the large number of points in Fig. 12(a) and Fig. 12(b) when BPNN and PSO-BPNN were adopted to conduct multi-objective optimization for steering system. There were few individuals in the population when GA-BPNN was used to optimize the steering system, which indicated that using GA-BPNN algorithm had obvious advantages.
Fig. 12Optimization processes of three kinds of algorithms
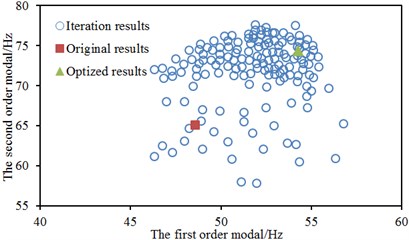
a) GA-BPNN
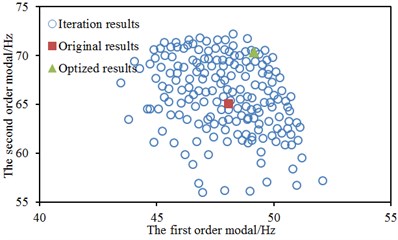
b) PSO-BPNN
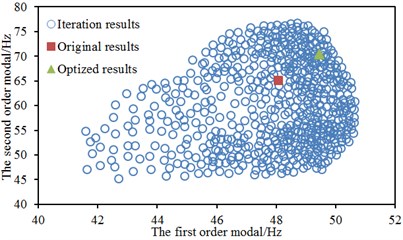
c) BPNN
Fig. 13Thickness of concerned parts on the optimized steering system
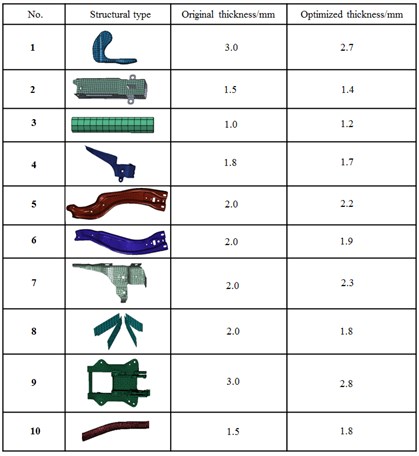
Through the above analysis, an optimal structure could be obtained when GA-BPNN was used to optimize the steering system. The top two order modal frequencies were 54.3 Hz and 74.3 Hz respectively, increasing by 5.7 Hz and 9.2 Hz compared with original results. The thickness of various parts of steering system after optimization was shown in Fig. 13. It could be seen from Fig. 13 that the thickness of most concerned parts after optimization was reduced while the thickness of some parts would increase accordingly. The mass of the optimized steering system was 10.3 kg, decreasing by 2.2 kg compared with the mass of the original structure.
Table 2Predicted results of three kinds of algorithms
Order | Original value / Hz | GA-BPNN | PSO-BPNN | BPNN |
1 | 48.6 Hz | 54.3 Hz | 49.2 Hz | 49.5 Hz |
2 | 65.1 Hz | 74.3 Hz | 70.3 Hz | 69.5 Hz |
Fig. 14Comparisons of accelerations at different points of steering wheel before and after optimization
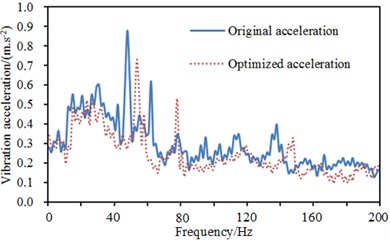
a) Point 1
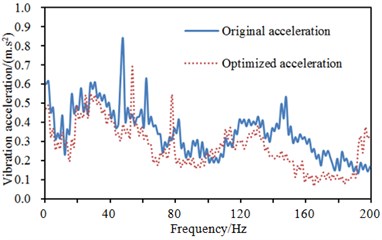
b) Point 2
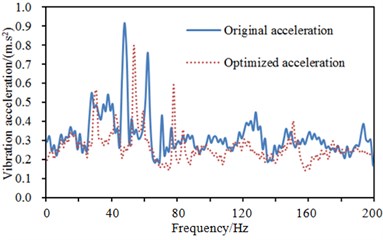
c) Point 3
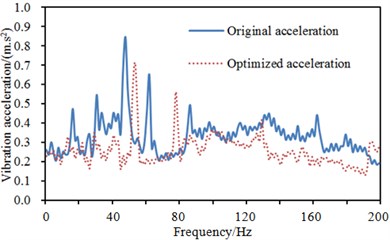
d) Point 4
Fig. 15The top two modes of steering system after optimization
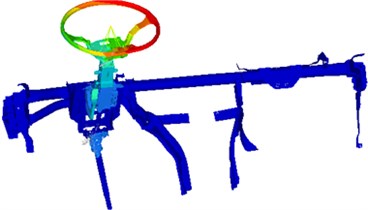
a) 54.3 Hz

b) 74.3 Hz
The optimized parameters were reapplied to the steering system to compute the vibration acceleration of many positions on the steering system and compare with that of the original structure. The result was shown in Fig. 14. As displayed from Fig. 14, vibration accelerations at many positions improved peak frequencies after optimization and the value of vibration accelerations decreased slightly at the majority of frequency points in the analyzed frequency band, which showed that it was effective to use GA-BPNN to conduct multi-objective optimization for the steering system. The top two modes of vibration of the steering system were extracted, as shown in Fig. 15.
5. Conclusions
1) This paper established the multi-body dynamics model of the steering system and obtained the random road spectrum of 4 wheels through mathematical model. Results showed that random road spectrums at different wheels were not totally the same and the position and size of peak values were also different. Therefore, the road spectrum of a wheel could not be used to replace the road spectrum of all wheels in multi-body dynamics simulation model. Otherwise, computational results would have a big error.
2) Vibration accelerations of the steering wheel at different positions were extracted through the multi-body dynamics model of steering system. Results showed that there were two obvious peak values on the curve of vibration acceleration, and peak frequencies were 48.6 Hz and 65.1 Hz. The measures must be taken to improve the two order resonance frequencies in order to eliminate the vibration phenomenon of steering system.
3) The finite element model of steering system was established to compute the vibration acceleration, and it was compared with the experimental result. Relative error was controlled within 5 %. It indicated that the finite element model in this paper was reliable. In addition, the computational two order modal frequencies were completely the same with the peak frequencies of vibration acceleration, which proved that the peak values of vibration acceleration were totally caused by the top two order modals.
4) GA-BPNN algorithm was proposed to optimize the structural thickness of key parts on the steering system, and the optimized result was then compared with that of BPNN and PSO-BPNN. Results showed that the optimization efficiency and result of GA-BPNN were obviously superior to those of other algorithms in the process of optimization and iteration. The optimized parameters were reapplied to the computational model of this paper. Vibration accelerations of the steering system at many positions were extracted to compare with those of the original result. Peak frequencies were significantly improved. In addition, vibration accelerations at most frequency points of the whole frequency band were significantly improved.
References
-
Kim K. W., Park J. B., Lee S. J. Tire mass imbalance, rolling phase difference, non-uniformity induced force difference, and inflation pressure change effects on steering wheel vibration. SAE Paper, 2005-01-2317, 2005.
-
Yu J. H., Nutwell B., Brickner B. Analysis of vehicle chassis transmissibility of steering shimmy and brake judder: system modeling and validation. SAE Paper, 2007-01-2341, 2007.
-
Yu J. H., Brickner B., Nutweell B. Analysis of vehicle chassis transmissibility of steering shimmy and brake judder: mechanism study and virtual design of experiment. SAE Paper, 2007-01-2342, 2007.
-
Tan W. J., Yang L., Wu X. R. Steering wheel shimmy optimization based on ODS analysis and experimental modal analysis. Journal of Vibration Engineering, Vol. 24, Issue 5, 2011, p. 498-504.
-
Zhou N., Li L., Dai S. L. Research of steering wheel swaying in high speed. Automotive Engineer, Vol. 11, 2011, p. 49-51.
-
Park H. B., Lee J. U., Suh J. K. Design of high stiffness steering system for idle vibration. KSAE Pring Conference, 1997.
-
Kim K. C., Choi I. H., Kim C. M. A study on the advanced technology analysis process of steering system for idle performance. SAE Paper, 2007-01-2339, 2007.
-
Lam K. P., Behdinan K., Cleghom W. L. A material and guage thichness sensitivity analysis on the NVH and crashworth of automotive instrument panel support. Thirrwalled Structures, Vol. 41, 2003, p. 1005-1018.
-
Wang Q. D., Jiang W. H., Chen W. W., Zhao J. Q. Simultaneous optimization of mechanical and control parameters for integrated control system of active suspension and electric power steering. Chinese Journal of Mechanical Engineering, Vol. 44, Issue 8, 2008, p. 68-73.
-
Zhou P., Yu D. J., Zang X. G., Yao L. Y. Optimization of the natural frequency of vehicle steering system using response surface method. Automotive Engineering, Vol. 32, Issue 10, 2010, p. 883-887.
-
Zhang Y. L., Xu X., Wu Y. Control on steering wheel shimmy of the car at high speed. Noise and Vibration Control, Vol. 2, 2011, p. 56-58.
-
Reed P. M., Hadka D., Herman J. D., et al. Evolutionary multiobjective optimization in water resources: the past, present, and future. Advances in Water Resources, Vol. 51, 2013, p. 438-456.
-
Erfani T., Utyuzhnikov S. V. Directed search domain: a method for even generation of the Pareto frontier in multiobjective optimization. Engineering Optimization, Vol. 43, Issue 5, 2011, p. 467-484.
-
Schutze O., Esquivel X., Lara A., et al. Using the averaged Hausdorff distance as a performance measure in evolutionary multi-objective optimization. IEEE Transactions on Evolutionary Computation, Vol. 16, Issue 4, 2012, p. 504-522.
-
Schutze O., Lara A., Coello C. A. C. On the influence of the number of objectives on the hardness of a multiobjective optimization problem. IEEE Transactions on Evolutionary Computation, Vol. 15, Issue 4, 2011, p. 444-455.
-
Deb K., Pratap A., Agarwal S. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, Vol. 6, Issue 2, 2000, p. 182-197.
-
Feng J. J., Luo X. Q. Application of genetic algorithm in optimization design for 2-D cascade by using singularities method. Proceeding of the CSEE, Vol. 22, Issue 11, 2002, p. 97-99.
-
Qian H. Z., Gu K. Q., Peng D. Multi-objective optimization design of ultra lightweight artillery cradle based on NSGA-II algorithm. Journal of Machine Design, Vol. 29, Issue 6, 2012, p. 36-39.
-
Yu T. F., Zhu H. Z., Peng C. H. Multi-objective optimization of a coal-fired boiler combustion based on NSGA-II algorithm. Journal of Nanchang University, Vol. 35, Issue 1, 2013, p. 58-61.
-
Shafaghat R., Hosseinalipour S. M., Nouri N. M. Shape optimization of two-dimensional cavitators in supercavitating flows, using NSGA-II algorithm. Applied Ocean Research, Vol. 30, Issue 4, 2008, p. 305-310.
-
Senthilkumar C., Ganesan G., Karthikeyan R. Optimization of ECM parameters using RSM and non-dominated sorting genetic algorithm. International Journal of Machining and Machinability of Materials, Vol. 14, Issue 1, 2013, p. 77-90.
-
Wang X. D., Kang S. Multi-objective optimization on the rotor of transonic axial compressor. Journal of Engineering Thermophysics, Vol. 32, Issue 11, 2011, p. 1847-1850.
Cited by
About this article
This work is supported by National Natural Science Foundation of China (61503049), China Postdoctoral Science Foundation Funded Project (2016T90838; 2015M582525), Specialized Research Fund for the Doctoral Program of Higher Education of China (20135522110003) and Open Fund of Chongqing Key Laboratory of Traffic and Transportation (2016CQJY004).
