Silage production technology using grass thickening vibratory method

1. Introduction

In agriculture, when preparing forage from grassy plants, we face the problem of how to thicken materials effectively and economically. When preparing forage, grass thickening mainly affects quality of the prepared forage. When thickening grass mass in a trench by a tractor, energy-consuming effect of thickening is rather high and reaches 18 kJ/kg [1, 2]. When pressing grass mass by various wheel tractors, in the first pressing stage grass mass deforms up to about 275 mm [2]. It has also been determined that, thickening with tractors, vertically operating pressure force increases under certain tractor’s engine rotation frequency. In the frequency range of 20-26 Hz, the measured speed of vibrations, if pressing grass by caterpillar tractor, increases by 5 dB, and by wheeled tractors up to 13 dB in reference to the static gravity force of these tractors. Research results indicate that during grass thickening stages, deformation decreases and the resonant frequency of the pressed grass increases [2].

In the case of vibratory thickening, the thickened mass is not polluted with petroleum products, and the danger of traumas is decreased. One of grass thickening method is the vibrating compaction using vibrating rollers. The rollers with vibratory rolling elements are used to achieve higher compaction rates when storing wilted grass or chopped maize in clamp silos. So, this method is suitable only for compacting in trenches and clamps rather than containers [3, 4].

Performed scientific research [1, 5] shows, that experimental vibrators with constant current engine and indirect vibrators with constant current engine are a good alternative for grass thickening. These procedures thicken effectively only bulk stem well chopped grassy plants and partly their mixtures. However, it is not recommended to thicken red clovers and Galega Orientalis with this equipment. When using vibratory thickeners, it is required to set the frequency correctly by which plant mass is pressed better and to determine what dynamic requirements of the equipment should be and how large an area of the silage it could press [6].

One of the indexes that characterises pressure of fibred-plant mass is its density. When performing research of the thickening process of fibred-plant mass, many authors adhere to the following preconditions: 1) quantity of the static load force does not depend on grass deformation speed; 2) pressure derivative according to mass density is a function of the added pressure. These preconditions are used in description of simplified grass mass pressure models [7]. Separate grass characteristics are described applying idealistic real rheological elements of materials and their various combinations [8]. In many cases, deformation and relaxation of elements in making a model are described by differential equations [5, 6]. These equations are usually complicated because elements of the pressed mass systems contain many degrees of freedom and many corresponding natural frequencies.

Many models were developed to analyse a viscous elastic material: Maxwell; Kelvin; Biurgers, Herschel-Bulkley, Bingham etc. In applying the Maxwell model, the advantage is that the volumetric and tangential modules can be assessed independently. Many authors used the equivalent mechanical components to model the stress-deformation relation of biological materials. The spring stiffness is shown to be non-linear and a friction element is recommended to model a fully plastic strain [9, 10]. It is possible to achieve good agreement between theoretical and experimental results [6]. But for practical issues these models are very complicated. This compaction task is simplified if a model of the vibrating system is constructed using a single degree of freedom according to the classical theory of mechanical oscillations [11, 12].

The objective of this research is to evaluate silage preparation in a container storage by inertia directional vibrator with vibratory thickening approach as well as to determine the vibrator movement characteristics in thickening silage by using a calculation model and then to verify with experimental data.

2. Theoretical analysis of silage thickening process

2.1. Peculiarities of fluctuations arisen by directional vibrator

Thickening the silage mass involves dealing with an elastically tenacious and partly coherent material with a relaxing characteristic. The elastic and viscous resistance forces are acted upon the vibrator that is thickening the silage mass. The analysis of the thickening process of fibrous plant mass is based on the following assumptions: the initial density of the silage is the same in cross-section around the bunker, stresses in all directions are equal to zero in the absence of external load forces, the silage density increases continuously during thickening process, static load forces do not affect the velocity of deforming silage and the pressure derivative according to mass density is the added pressure function [5]. In this environment, the vibrator movement is difficult to describe mathematically and it is not possible in many of the cases.

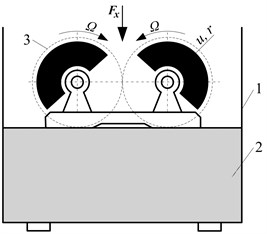
According to the classic vibration theory, it is possible to scrutinise the system of plant thickening by vibratory method as a concentrated mass on a spring when it’s other end is steadily set [13]. One of the most common dynamic inputs is excitation by a centrifugal force of non-weighted masses [11, 12]. By requiring the excitation force to be oriented in a certain direction, an appropriate vibrator construction is needed. In the present study, a direct-action vibrator, in which the excitation force is directed to a vertical straight line as shown in Fig. 1, has been chosen.

Fig. 1Scheme of silage thickening process with direct-action vibrator: 1 – a container store; 2 – silage mass; 3 – inertia direct-action vibrator

The excitation force in vibration vertical direction is [12, 13]:

1

$F_x=2ur{\mathrm{\Omega }}^2\cos \mathrm{\Omega }t,$

where an $u$ is the unbalance system mass (kg), $r$ is the radius (m), $\mathrm{\Omega }$ is the frequency of excitation force (rad/s).

Amplitude of excitation force is not constant since it depends on rotational frequency. Denote the frequency ratio $\eta =\mathrm{\Omega }/{\omega }_0\mathrm{}$. Then, the amplitude of excitation force can be expressed as:

2

$\widehat{F}=2ur{\mathrm{\Omega }}^2=2ur{\omega }_0^2{\eta }^2,$

where ${\omega }_0=\sqrt{k/m}$ is the natural angular frequency (rad/s) of the vibrator.

In this system, resistance elements of mass elasticity and its inner friction are separated from each other. Then, the governing differential equation of motion can be written as [13]:

3

$m\ddot{x}+c\dot{x}+kx=2ur{\omega }_0^2{\eta }^2,$

where $m$ is the vibrator mass (kg), $k$ is the stiffness of the spring (N/m), $x$ is the displacement of the spring (m); $\dot{x}=dx/dt$ is the velocity of vibration (m/s); $\ddot{x}=dv/dt$ is the acceleration of vibration (m/s²), $c$ is the constant of mechanical resistance (Ns/m), $t$ is the time (s).

The total solution of this equation has two parts: the first part corresponds to free vibrations of the system which, in this case decays quickly due to internal friction of the system; the second part is response due to dynamic force action and in this case, is the dominant vibration. Having expressed the vibration response in a complex form, we can find the relation between vibration velocity and excitation force. By knowing the mechanical resistance of the grass mass and having measured the vibration speed, it is possible to set $F_x$ values of excitation force, and then compare these equations to the calculated ones.

2.2. Numerical analysis of grass thickening using vibratory method

In developing the numerical models, which do not seek to replicate a complex heterogeneous material, reasonable simplifications can be implemented. Then, the analysis task becomes much simpler. This method gives a higher error, but it is sufficient to describe the silage compaction process by a vibrator for practical engineering applications. Despite the fact that silage does not have a homogeneous mass, reasonable simplifications can be implemented. Due to the fact that silage mass internal stresses are relatively low, the homogeneity assumption can be implemented to model silage mass. Then, a linear relationship between stress and deformation can be obtained with sufficient accuracy [14, 15].

For the numerical analysis, the initial phase of the excitation force magnitude, frequency, stiffness coefficient of the surrounding (silage) and damping coefficient need to be chosen. While evaluating work of the vibrator, initially the silage stiffness coefficient (e.g. 300 N/m) has been chosen and then it was increased at every second (in real conditions, silage stiffness coefficient changes continuously) [16]. Silage damping coefficient can be chosen from the information in literature. In the present study, silage damping coefficient is taken as 7 s^-1 [16]. The vibration frequency was increased from 1 Hz to 30 Hz in increments of 5 Hz.

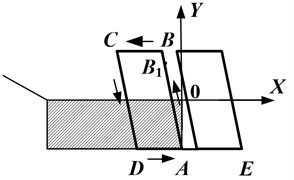
Vibrator sinking depth into the silage mass schematically is shown in Fig. 2. Solid body (1) (vibrator) is pressed among two slabs (silage mass) (2). Springs (3) model the silage mass stiffness characteristics. Relation between the body (1) and slabs (2) is described only by cohesion and friction forces $Q\text{'}$. The concepts of the present study are that lateral frictional forces to the surrounding are primary and resistance force on the base of the vibrator is insignificant. Depending on the vibrator sinking depth, surrounding reaction is shown graphically in outline ABCDE (Fig. 3). Vibrator sinking into the surrounding during one excitation force cycle is shown at segment AE. Here $x$ is the direction of a movement generated by the centrifugal force. If external excitation force $F$, which influences body 1, does not exceed $Q\text{'}$ – coupling and friction forces to the silage mass are in quiescent state – i.e. $F<Q\text{'}$ – the vibrator moves only in the frame of silage mass thickening deformation that is imitated by springs 3 (Fig. 2). It is observed along sides AB and CD of the outline (Fig. 3). If excitation force F exceeds force $Q\text{'}$ ($Q\text{'}=$ constant), movement of the vibrator (1) in respect of slabs (2) (Fig. 2). It corresponds to movement of the vibrator in respect to the silage mass along segments BC and DE (Fig. 3). The specified condition $Q\text{'}=Q$ ($Q$ – constant vibrator friction force to the silage mass ($N$)), signifies the temporary silage mass resistance [5]. At some time instant, velocity of the vibrator equals to zero (before reaching point B₁) at the segment AB (Fig. 3). Then, depending on the vibrator’s pressure on the grass, grass reaction is represented by the outline AB₁AE. If the amplitude of vibration is less than plastic deformation limit, vibrator’s sinking into the grass should stop. Movement is considered to be steady since temporary resistance during the period of the excitation force $F$ action is decreasing (external excitation force $F$ have vertical direction in y axis, and axis of vibrator – in $x$ axis).

Fig. 2The model of vibrator sinking into material: 1 – hard solid, 2 – slabs (silage mass), 3 – springs vibrator sinking

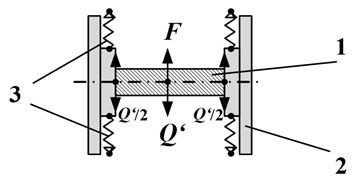
Fig. 3The surrounding reaction along the path of the vibrator sinking depth

The theoretical model of vibrator movement for the case shown in Fig. 3 was deeply analysed in ref. [5]. The Eq. (4) is a more complete representation of vibrator movement in silage grass thickening that includes the characteristics of silage stiffness and motion suppression [5]:

4

$\ddot{x}+2n\dot{x}+p^{2}x=g\left(1-q\right)+fg\mathrm{s}\mathrm{i}\mathrm{n}(\omega t+{\alpha }_0),$

where $x$ is the displacement of the vibrator base (m), $\dot{x}$ is the velocity of the vibrator (ms^-1), $\ddot{x}$ is the acceleration of the vibrator (ms^-2), $n$ is the damping coefficient (s^-1), $p$ is the system vibration frequency (Hz or s^-1), $g$ is the gravity acceleration, $\omega$ is the frequency of the excitation force (Hz or $s$^-1), ${\alpha }_0$is the initial phase of the excitation force (rad), $q=Q/P$,$P$ is the weight force ($N$), $f=F/P$, $F$ is the excitation force ($N$), $t$ is time ($s$).

Satisfying the initial conditions at point A ($x=\dot{x}=0,t=0$) the velocity was obtained:

5

$\dot{x}=\frac{fg\omega }{{(p^2-{\omega }^2)}^2+4n^2{\omega }^2}\left[\left(p^2-{\omega }^2\right)\cos \left(\omega t+{\alpha }_0\right)+2n\omega \mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t+{\alpha }_0\right)\right].$

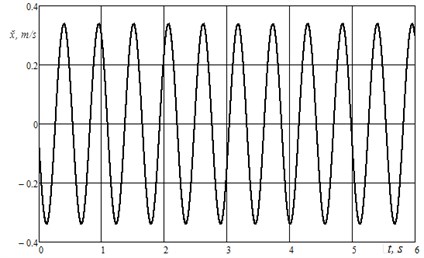
Using the Eq. (5) the velocity of the vibrator sinking into the silage mass is plotted in Fig. 4. The graph was obtained using the programme package Mathcad. We can observe that velocity amplitude of the vibrator sinking into the silage is 0.34 m/s (Fig. 4) when vibration frequency was increased till 27 Hz.

The performed theoretical study of the vibratory thickening process of silage and similar other resilient materials allows to describe the process by analytical means where approximate values of system coefficients can be chosen and reasonable simplifications can be introduced. It is possible to set the influence of the vibrator’s technical parameters to the silage or grass thickening dynamics. The developed theoretical model can be used for preparation of a technical task when designing a vibratory thickening installation. The theoretical solutions can be improved by selecting more accurate values for the various system parameters.

Fig. 4Vibrator sinking velocity into silage diagram: dependence of vibrator movement velocity (m/s) and vibration time (s)

3. Experimental investigation of silage thickening using vibratory method

For experimental study, the centrifugal direct-action vibrator with two masses rotating in counter-clockwise directions was used for silage preparation. Direct-action vibrators have two weights rotating in different directions at the same angular frequency. Direct-action vibrators are designed in the Institute of Agricultural Engineering at Aleksandras Stulginskis University (Lithuania) and suitable for silage compaction. The vibrator was rotated by an asynchronous motor of 1.1 kW, 1500 min^-1. Weights of 7.0 kg mass were fitted to rollers in the vibrator and the total mass of this vibrator was 125 kg (Figs. 5-6). The container was filled by chopped maize mass as shown in Fig. 6.

Fig. 5Scheme of silage thickening using centrifugal direct-action vibrator: 1 – container storage; 2 – centrifugal direct-action vibrator; 3 – electrical engine; 4 – weights; 5 – accelerometer; 6 – vibrator cover; 7 – electric current frequency converter; 8 – tensometer sensor; 9 – pressure measurement device; 10 – PC with Pulse software; 11 – mass of compacted plants

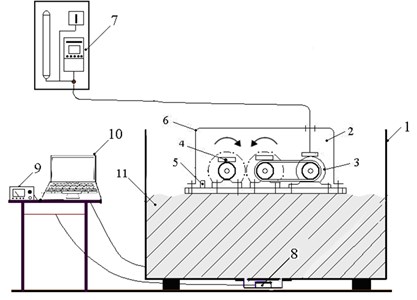
The dimensions of container storage; width is 0.75 m; length is 1.20 m; height is 0.95 m). The plant mass has a moisture content of 70-80 % and chaff length of 15-45 mm. The vibrator was installed on the top and continuously operated for 10-20 minutes. While the vibrator was working, every 5 minutes the thickness of the mixture was recorded by measuring instruments. The plant mass volume in the container was calculated using measurements by a ruler (accuracy ±0.001 m) at four selected points [1]. The plant mass in the container was determined by scales, having the range of 0-100 kg, and accuracy of ±0.1 kg.

The vibrator accelerations on the vibration plane of the direct-action vibrator were measured. Acceleration and velocity of the direct-action vibrator was measured according to the widely accepted methodology by using a components PULSE software developed by Brüel&Kjær was used along with PULSE data acquisition module 3580, and type 4370 piezoelectric charge accelerometers for recording vibration data (see Fig. 5). The characteristics of accelerometer type 4370: frequency range is 0.1-4800 Hz; sensitivity is 100 pC/g. The location of accelerometer is presented in Fig. 6. Each experiment was repeated at least 3 times at the 1-27 Hz range. The test results were analyzed by statistical methods where the arithmetic means, the standard deviation were calculated and the error was estimated by selecting Student distribution coefficient with a probability of 0.95.

Fig. 6Centrifugal direct-action vibrator in container storage: 1 – location of accelerometer

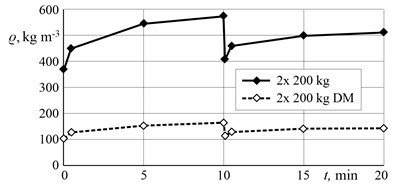
It was estimated that better silage is obtained when the plant mass has a higher density. In previous studies, it has been established that silage was compacted better by loading a thicker layer [1]. The influence of maize mass density variation to thickening time has been determined (see Fig. 7). The first 200 kg corn layer corresponds to 10 minutes thickening period and the second additional 200 kg layer corresponds to a repeated 10 minutes thickening. After 20 minutes of thickening, a density of 510 kg/m³ has been obtained for both layers, while thickening the first 200 kg mass mixture layer after 10 minutes the density was 571 kg/m³. Dry matter (DM) densities correspond respectively to 143 and 161 kg/m³. For this test, the resulting silage density was sufficient.

Fig. 7The influence of maize mass density and thickening time during compaction by direct-action vibrator

When analysing the homogeneous differential equation of a single degree freedom of a linear stationary system, it is known that the resonant properties depend on the system mass, stiffness of the spring and amplitude characteristics depend on the mechanical resistance coefficient (i.e., internal friction of silage mass) [10]. In order to confirm these observations, the vibration acceleration of direct-action vibrator was measured on the vibration plane. Previous results showed that a high acceleration is one of the most important settings for providing the highest density in a reasonable amount of time [1, 6]. The amplitude of vibratory device vibration depends on the device design and the position of eccentric installation. After the evaluation of herbal plant specific characteristics it was selected the vibratory device design, set the frequency range and amplitude. It was found that for maize thickening by direct-action vibrator the greatest acceleration was obtained at the frequency of 15 Hz.

In Figs. 8-9 presented vibration movement velocity and acceleration of direct-action vibrator was measured by accelerometer fitted on the vibration plate, and all experimental data were fixed by PULSE software. As this PULSE software uses Excel program the data was exported and analysed by Excel software. The duration of separate experiments was 5 min., but results in Figs. 8-9 are presented only for 2 s range, because all research results on all working period were very similar.

Fig. 8Vibrator movement velocity

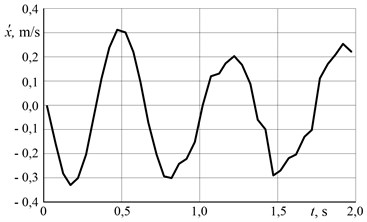
Fig. 9Vibrator movement acceleration

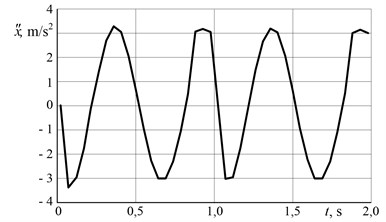
With the increase of silage thickness, vibration velocity and acceleration of the vibrator sinking into the grass do not decrease significantly (see Figs. 8-9). Velocity was varied from 0.3 till 0.2 m/s. It was observed that with the increase of silage density, velocity decreases insignificantly. Acceleration was about 3 m/s² at all work cycle. At the end of the work cycle, velocity of the vibrator movement is decreased by minimal value (about 0.1 m/s). This can be explained by the fact that velocity of the vibrator movement is quite high since the vibrator is constantly under excitation force. It can be seen from Fig. 8, the maximum value of velocity amplitude is 0.32 m/s². The theoretical results were 0.34 m/s².The difference between the simulation and experimentally established results was less than 10 %. Thus, the percentage errors are within the accepted ranges. The validity of the simulation data, after performing the simplified dynamic analysis of the silage thickening by vibrator, has been confirmed.

Evaluated simulation method can be recommended for development of the herbaceous plants silage thickening process by vibratory method. Based on the presented results, it is possible to determine practically operational regimes of direct-action vibrator, movement velocity, acceleration and other operational characteristics.

The role of each co-author to the paper preparation. Eglė Jotautienė was one of supervisors of this work, performed part of Information sources review, analyzed vibratory thickening equipment, prepared part of theoretical models and analytical tests methodology of vibratory thickening equipment and together with co-authors performed their experimental tests, managed research data in the graphs and conducted the analysis of these results and formulation of conclusions. Algirdas Jasinskas was the research supervisor of this work, he performed part of Information sources review, prepared article methodical part, has organized and together with co-authors carried out the experimental and analytical studies with inertia vibrators, investigated the silo compaction process in a container storage, managed research data and presented research results in graphs, as well as performed their discussion, analysis and the formulation of conclusions. The author’s great contribution of paper layout design according to requirements, correcting, etc. Vytautas Kučinskas investigated vibratory compaction equipments, prepared their work and silage compaction research methodology, together with co-authors performed their analytical and experimental studies, analyzed vibratory compaction unit working process and conducted research results analysis and formulation of conclusions. Dainius Steponavičius analyzed the sources of information, presented theoretical assumptions of vibrational compaction equipment working process, analyzed vibratory thickening equipment, prepared part of theoretical models and analytical tests methodology, presented part of survey data of vibratory compaction equipment and conducted their analysis and formulation of conclusions.

4. Conclusions

A numerical and experimental analysis was performed to analyse the silage vibration thickening process. According to a classic vibration theory, it is possible to model the system of silage thickening by vibratory method as a linear stationary system of one degree of freedom.

The performed numerical research of silage thickening indicates that velocity amplitude of the vibrator sinking into the silage is 0.34 m/s. Experimentally obtained results of vibrator movement velocity was varied from 0.32 till 0.2 m/s and it show a decrease of a minimal value (about 0.1 m/s). This difference is due to the fact that the numerical analysis of this process was performed by choosing approximate values of some coefficients and introducing various simplifications.

The difference between the numerical simulation and experimentally obtained results was less than 10 %. This reasonable calculations method for practical issues can be recommended for the development of the silage thickening process. Based on the given results, it is possible to determine practical operational regimes of direct-action vibrator as movement velocity, acceleration and other operational characteristics.