The interaction of the freight car and way taking into account deformation of assembled rails and sleepers

Abilkaiyr, Zhastalap; Musayev, Janat; Kaiym, Talgat; Alpeisov, Azamat; Alimbetov, Assylkhan; Zhauyt, Algazy

Vibroengineering Procedia

Browse Procedia

Published: 07 October 2016

Check for updates

The interaction of the freight car and way taking into account deformation of assembled rails and sleepers

Zhastalap Abilkaiyr¹

Janat Musayev²

Talgat Kaiym³

Azamat Alpeisov⁴

Assylkhan Alimbetov⁵

Algazy Zhauyt⁶

¹Kazakh Academy of Transport and Communications named after M. Tynyshpayev, Almaty 050012, Kazakhstan

^{2, 3, 4, 5, 6}Kazakh National Research Technical University named after K. I. Satpayev, Almaty 050013, Kazakhstan

Corresponding Author:

Janat Musayev

Cite the article Download PDF

Downloads 1358

Abstract

The settlement scheme is made and analytical researches of fluctuations of crew under the influence unevenness of the way in the horizontal and vertical planes taking into account impact of the railroad car on the way are executed.

1. Introduction

The design and creation of reliable construction designs of railroad cars requires carrying out numerical mathematical calculations. Carrying out analytical calculations is impossible without drawing up mathematical models describing interaction of the way and the rolling stock [1]. The railway track is a difficult design which works under conditions of long influence of series of short-term loadings. The size and the nature of action of loadings are caused by the construction design of the way and a vehicular part of the rolling stock. Therefore, methods of calculation of the way are based on the works which are conducted in two interconnected areas [3-4]. The lack of rigid communication of sidewalls of the cart of the freight car of 18-100 type causes deformation of the cart in the plan. This deformation is resisted by flexible frictional communications in knots of spring suspension and friction between axle boxes and sidewalls of the frame [5-6]. The accounting of the running of sidewalls in the analytical model significantly complicates mathematical model of the cart. At the same time introduction of specifications which owing to big uncertainty of stiffening and frictional parameters, have more qualitative, than quantitative character is required [8]. When calculating forces, operating on the way for simplification of the analytical model it is generally accepted the cart of the freight car to consider a rigid rectangle. Such assumption increases the given rigidity in interactions of a wheel with a rail. It leads to some increase in calculated values of forces when determining side loads of the way [9-10].

2. The unevenness of the way in the horizontal plane

The executed researches show rather good coincidence of the design data obtained by means of such models with results of various experiments. It proves possibility of usage of the developed mathematical model for the analytical research of interaction of the freight car and the way with various deviations. Continuous horizontal and vertical unevenness of the way have casual character and consist of two types of unevenness – geometrical and elastic. Measurement of horizontal unevenness in comparison with vertical is more complex challenge. It is caused by the fact that their size is very small in comparison with track width. Therefore, higher precision of measurement is necessary. Traditional high-speed track measuring systems, for example ARSRIRT, have devices for entry of both rail threads in the plan (see Fig. 1). Horizontal unevenness of rail threads is registered to similarly vertical unevenness that doesn't give sufficient accuracy of measurement. For record of movements of vertical and horizontal unevenness in the Kazakh academy of transport and communications transformer sensors which have a straight-line characteristic are developed and tested. Sensor device is quite simple: the ferrite core is inserted into the ebonite core, the cable with a diameter of 0.09 mm from two windings is reeled up to the first on the framework, the alternating voltage is brought of 30 V with a frequency of 10 kHz. The measuring coil consists of two parts with identical number of rounds. The oscillograph loop is connected between an average point of a winding and the diode. Relative movements of position of cores of transformer sensors are proportional to a beam deviation on the tape of the oscillograph.

Fig. 1Installation of the sensor of horizontal and vertical movements on the railroad car

For the research of the movement of the body of the railroad car of rather railway line on trailer beams three devices with five sensors are installed. Sensors register vertical movements in three dimensions cross movements of the body concerning heads of rails are registered in two measurements. Horizontal unevenness of the way is measured by two sensors which interact with the top working side of the rail. The analysis of functions of distribution of horizontal unevenness shows that distribution of unevenness approaches the normal law of Gauss. If to designate casual influence of horizontal unevenness through $h (t)$ , then at Gaussian distribution density of probability will be defined by expression:

1

F (h) = \frac{1}{σ \sqrt{2 π}} e^{\frac{- (h - m_{h})^{2}}{2 σ^{2}}},

and integrated function of distribution by a formula:

2

F (h) = \frac{1}{σ \sqrt{2 π}} \int_{- \infty}^{\infty} e^{\frac{- (h - m_{h})^{2}}{2 σ^{2}}} d h,

where $σ$ – mean square deviation of a random variable; $m_{h}$ – expectation value.

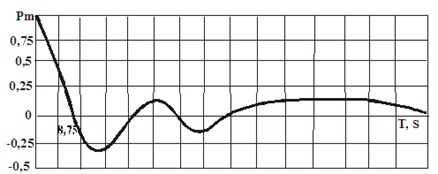
For assessment of statistical properties of influence of casual geometrical unevenness serve correlation function and spectral density. Correlation function characterizes an interconnection between values of casual unevenness in different time points. On the realization of horizontal unevenness in the calculated way, we will receive the schedule of rated correlation function of influence of unevenness (see Fig. 3).

3. Analytical study of the dynamic processes of interaction and ways of wagon

It follows from the schedule that with increase in time of correlation communication the size of correlation function quickly decreases and at $τ =$ 8.75 s reaches zero, there is a slow attenuation of correlation function (see Fig. 3). It demonstrates existence in a range of frequencies of unevenness of periodic character. Owing to existence in spring sets of elements with nonlinear characteristics, the real crew represents vibrating system in which all types of fluctuations are interconnected. Therefore, at research of fluctuations of crew under the influence of unevenness of the way in the horizontal and vertical planes the analytical model accepting for creation of mathematical model of the freight car can be submitted by system with nine degrees of freedom (swaying and wagging of each of carts, and also swaying, wagging, side rolling, jumping and galloping of the body). In this case it is impossible to separate a choice of system of the generalized coordinate’s part of the equations, having simplified thereby mathematical model just as it is done at research of stability of the movement of crew [2]. Simplification of the analytical model due to rejection of the degrees of freedom of the body relating to its fluctuations in the vertical longitudinal plane is possible only in case of the analysis of additional influence on horizontal forces of interaction of unevenness of the way in the plan. Similarly, for the analysis of influence only of vertical unevenness of the way, on fluctuations of the body of the railroad car in the vertical longitudinal and cross planes consider simplified model considering only these three degrees of freedom. However, such simplified models don't allow to consider interaction of crew of and railway track with simultaneous deviations both in horizontal, and in vertical planes, to estimate stability from a re railing of the wheel on the top of the rail and accumulation of deformations in the way. It is enough to complete a mathematical model to assess the impact speed and actual deviations in the way of traffic safety and dynamic processes of interaction of freight railroad car and way should consist, as minimum of nine ordinary second order differential equations describing the oscillations of the crew and hybrid system of rail grid deformation equations of the assembled rails and sleepers.

The analytical model of crew is submitted in the Fig. 2. For the cart CRI-ХЗ of the scheme differ only in character of forces, operating between truck bolster and sidewalls. At the description of mathematical model are used symbols and systems of coordinates recommended to Bureau of pilot studies of the International Union of the railroads (BEI UIC) and a little added taking into account specifics of the considered tasks [3-4].

Fig. 2The analytical model of the freight car on carts with the central suspension

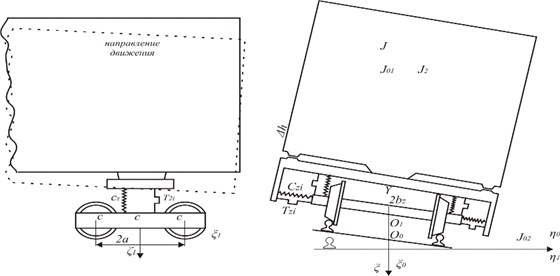
The system of the differential equations is made taking into account that according to the accepted premises, wheel couples cannot be displaced concerning sidewalls, and as the generalized coordinates of crew cross movements of the span body and centers of carts, turns of carts, the corner of side rolling of the body and vertical span movements are accepted.

The system of the differential equations in this case has appearance:

3

m {\ddot{y}}_{J} = Q φ_{O J} - Y_{i j} - m ν {\dot{ψ}}_{O J} + \sum_{i . j}^{2} Y_{J i j},

4

J_{z} {\ddot{ψ}}_{J} = a \sum_{j} (H_{J 1 j} - H_{J 2 j}) - \sum_{i} Q 2 b_{A} η_{J i} [\frac{b_{A}}{ν} ψ_{J} + \frac{ν}{r} (y_{J i} - \frac{Δ σ_{J i 1} + Δ σ_{J i 2}}{2} - {\bar{y}}_{J i}^{T})]

+ |M_{J}| s i g n (ψ - ψ_{J}),

\frac{1}{4} (m + \frac{J_{z}}{a^{2}}) {\ddot{y}}_{h j} = 0.25 Q \sum_{J} φ_{O j} - 0.5 m h \ddot{φ} - \frac{1}{4} (m + \frac{J_{z}}{a^{2}}) ν {\dot{ψ}}_{o j} - \frac{1}{4} (m - \frac{J_{z}}{a^{2}}) \times ({\ddot{y}}_{h j \pm 1} + ν ψ_{o j \pm 1})

- \frac{(- 1)^{J}}{2 a} \sum_{J} M_{J} s i g n (\dot{ψ} - {\dot{ψ}}_{J}),

\frac{1}{4} (m + \frac{J_{y}}{a^{2}}) {\ddot{z}}_{J} = \sum_{j}^{2} F_{J i} - \frac{1}{4} (m - \frac{J_{y}}{a^{2}}) {\ddot{z}}_{j \pm 1},

J_{x} \ddot{φ} = - \sum_{J}^{2} [(F_{J 1} - F_{J 2}) b_{z} + Y_{i j} h], \dot{J} = 1, \dots, 2,

5

Y_{J i j} = \{\begin{array}{l} - η_{j i} Q_{J i j} \frac{1}{ν} U_{y j i} for |y_{J i}| \leq σ_{J i j}, \\ E J_{z} (\frac{\partial^{3} y_{i}}{\partial x^{3}} {|_{X_{J i} + 0} - \frac{\partial^{3} y_{i}}{\partial x^{3}}|}_{X_{J i} - 0}) for |y_{J i}| \geq σ_{J i j}, \end{array} j = \{\begin{array}{l} 1 for y_{J i} \geq 0, \\ 2 for y_{J i} \leq 0, \end{array}

U_{y J i} = {\dot{y}}_{j i} - (- 1)^{i} a {\dot{ψ}}_{j} - ν ψ_{j},

F_{j i} = C_{z} [0.5 \sum_{i}^{2} ζ_{J i j} - Z_{J} + b_{z} φ (- 1)^{j}] + F_{T P} s i g n [0.5 \sum_{i}^{2} ζ_{J i j} - {\dot{Z}}_{J} + b_{z} \dot{φ} (- 1)^{j}],

E J_{ω} \frac{\partial^{4} φ_{j}}{\partial x^{4}} - C \frac{\partial^{2} φ_{j}}{\partial x^{2}} + J_{P} \frac{\partial^{2} φ_{j}}{\partial t^{2}} + m_{P} h_{3} (\frac{\partial^{2} y_{j}}{\partial t^{2}} + h_{3} \frac{\partial^{2} φ_{j}}{\partial t^{2}}) + N h_{3} (\frac{\partial^{2} y_{j}}{\partial x^{2}} + h_{3} \frac{\partial^{2} φ_{j}}{\partial x^{2}} + \frac{1}{R})

+ \sum_{K} M_{j k}^{0} δ (x_{k}) = \sum_{n} M_{j n} δ (x_{n} + ν t),

E J_{z} \frac{\partial^{4} y_{j}}{\partial x^{4}} - m_{P} (\frac{\partial^{2} y_{j}}{\partial t^{2}} + h_{3} \frac{\partial^{2} φ_{j}}{\partial t^{2}}) + N (\frac{\partial^{2} y_{j}}{\partial x^{2}} + h_{3} \frac{\partial^{2} φ_{j}}{\partial x^{2}} + \frac{1}{R}) + F_{j k}^{0} δ (x_{k})

= \sum_{n} Y_{j n} δ (x_{n} + ν t),

m_{P} \frac{d^{2} y_{n j k}}{d t^{2}} - F_{j k}^{0} + F_{Π K} ({\dot{Δ}}_{n k j}, {\dot{Δ}}_{n k j}) = 0, m_{i} \frac{d^{2} y_{i k}}{d t^{2}} - \sum_{j}^{2} F_{Π K} ({\dot{Δ}}_{n k j}, {\dot{Δ}}_{n k j}) + R_{Π K} = 0,

E F \frac{\partial^{2} W}{\partial x^{2}} - [m_{P} + 0.5 m_{i} δ (x_{i j})] \frac{\partial^{2} W}{\partial t^{2}} = N_{0} δ (x_{K}) - T_{n} δ (x_{n} + ν t),

j = 1,2, 3,4, \dots, n = 1,2, 3,4, \dots, k = 1,2, 3,4, \dots

In the equations mixture of the center points of the body coefficients at the corresponding accelerations represent the given part of mass of the body. If the base of the body is equal to the specified length of the corresponding physical pendulum, this size corresponds to the mass of the replacing point [6].

In most cases for freight cars and locomotives the size of a half of base of the body differs from its radius of inertia no more than for 20 %. Therefore, for carrying out approximate calculations in a number of cases it is possible to assume that these sizes coincide. The system of the equations in that case breaks up to two independent systems, each of which describes fluctuations of the truck with the specified weight falling on:

6

m_{п р} = 0.25 (m + J_{z} / a^{2}) .

Fig. 3Schedule of rated correlation function of horizontal unevenness of the site of the way 1500 m long

4. Conclusions

The provided analysis of forces of interaction showed that the calculation error caused by such simplification usually doesn’t exceed 10-15 %. The revolting functions in the model are: curvature of the way, change of width of the rail track and vertical provisions of rails. Now with serial track measuring cars are registered in pure form only width of the rail track and curvature of the way and vertical unevenness of the rail threads are estimated indirectly through arrows of the bend, sags and level. So, the chosen analytical model and presented mathematical model for an assessment of influence of speed and actual state of the railway track on traffic safety of crews, with sufficient degree of accuracy describes both fluctuations of the rolling stock, and deformation of the assembled rails and sleepers under the influence of periodic rolling load.

References

Ishida M., Ban T., Iida K., Ishida H., Aoki F. Effect of moderating friction of wheel/rail interface on vehicle/track dynamic behavior. Proceedings of the 7th International Conference on Contact Mechanics and Wear of Rail/Wheel Systems, Brisbane, Australia, 2006, p. 227-233.

Search CrossRef
Ohno K., Ban T., Obara T. Improvement of adhesion between wheel and rail by ceramics particle injection. Iridologists, Vol. 41, 1996, p. 973-978.

Search CrossRef
Tomeoka M., Kabe N., Tanimoto M., Miyauchi E., Nakata M. Friction control between wheel and rail by means of on-board lubrication. Wear, Vol. 253, 2002, p. 124-129.

Search CrossRef
Fischer F. D., Werner E., Knothe K. The surface temperature of a half plane heated by friction and cooled by convection. Journal of Applied Mathematics and Mechanics, Vol. 81, 2001, p. 75-81.

Search CrossRef
Bucher F., Theiler A., Knothe K. Normal and tangential contact problem of surfaces with measured roughness. Wear, Vol. 253, 2002, p. 206-220.

Search CrossRef
Ekberg A., Kabo E., Andersson H. An engineering model for prediction of rolling contact fatigue of railway wheels. Fatigue and Fracture of Engineering Materials and Structures, Vol. 25, 2002, p. 899-909.

Search CrossRef
Karttunen K., Kabo E., Ekberg A. A numerical study of the influence of lateral geometry irregularities on mechanical deterioration of freight tracks. Journal of Rail and Rapid Transit, Vol. 226, Issue 6, 2012, p. 575-586.

Search CrossRef
Chaar N., Berg M. Vehicle-track dynamic simulation of a locomotive considering wheel set structural flexibility and comparison with measurements. Journal of Rail and Transit, Vol. 219, 2005, p. 225-238.

Search CrossRef
Burstow M. C. Whole Life Rail Model Application and Development for RSSB – Continued Development of an RCF Damage Parameter. Rail Safety and Standards Board, Issue 2, Report EATR-S-2004-880, 2004.

Search CrossRef
Ekberg A., Kabo E., Karttunen K., Lindqvist B., Lundén R., Nordmark T., Olovsson J., Salomonsson O., Vernersson T. Identifying the root causes of damage of the wheels of heavy haul locomotives and its mitigation. Journal of Rail and Rapid Transit, Vol. 228, 2014, p. 663-672.

Search CrossRef

About this article

Received

24 July 2016

Accepted

12 September 2016

Published

07 October 2016

SUBJECTS

Vibration in transportation engineering

Keywords

railroad car

wagons

way

interaction

analytical model

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.