Difficulties in computational modelling of piston/liner interaction

2.1. Mapping

The computational grid of contact forces between piston and liner is fixed to the piston body – let us call it piston computational grid. The piston is performing reciprocating motion relative to the liner. The contact forces calculated on piston computational grid are function of gap between piston and liner, which is dependent on the liner deformation and true shape – it has to be mapped onto the piston computational grid. To do so, bicubic Hermite spline is employed:

where $f\left(t,u\right)$ is the target function; $h_{ij}$ and $g_{ij}$ are Hermite functions; $f_{ij}$ are the source function values; $s_{ij}$, $l_{ij}$, $k_{ij}$ are derivatives in $x$, $y$ and $xy$ direction. Function $f\left(t,u\right)$ is continuous through the second derivative, so the deformation shape can be mapped very smoothly.

As the deformation of the liner has to be mapped onto piston computational grid, forces of piston computational grid have to be mapped onto the liner grid as well. In this case, situation slightly differs. Calculated forces result in the overall forces and moments in each direction. Load applied onto the liner is a reaction of the piston load. Therefore, the overall forces and moments acting on piston computational grid should be equal to the overall forces and moments acting on the liner grid. To fulfill this static equivalence condition, different approach of mapping was used. First of all, discrete field of pressures calculated on the piston computational grid has to be reconstructed to the analytical form:

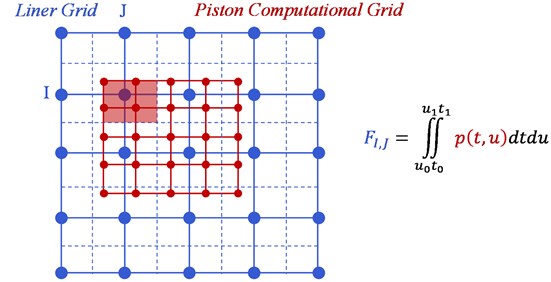
where $p\left(t,u\right)$ is the target function, $p_{ij}$ are the source function values and $N_{ij}$ are shape functions. To obtain nodal forces acting in the liner grid, function $p\left(t,u\right)$ has to be analytically integrated in a boundaries of a dual grid of a corresponding liner grid node, evident in Fig. 1.

Fig. 1Load mapping by analytical integration

2.2. Elastic deformation and Jacobian evaluation

Elastic deformations have significant impact on the piston dynamic behavior [5]. MBD uses Component Modes Synthesis in order to obtain elastic deformations of each flexible body – the overall deformation is a linear combination of mode shapes multiplied by the modal factors. Number of modal factors is the same as the mode shape count, which is related to the reduced number of degrees of freedom (DOF). In case of flexible piston with flexible piston skirt nodes of $m\times n$ count, there are $m\times n$ additional (radial in case of piston and liner) DOFs introduced into the simulation.

2.3. CPU time analysis

MBD solves equation of motion by numerical integrator based on, e.g. Newmark or HHT method. In this procedure, the Jacobian has to be evaluated for each iteration. Jacobian represents the dependency of function on each DOF. In practice, if there is DOF of $m\times n$ count, solver has to be called $m\times n$ times to evaluate each partial derivative. This is the main cause of very time-demanding piston/liner simulations developed by the authors.

User-written subroutine, which uses deformation inputs given by the MBD solver and gives outputs of force reactions back to the MBD solver, is called every time when each Jacobian cell needs to be evaluated. For instance, subroutine consists of its own hydrodynamic iterative solver, which takes approximately 200 iterations to converge. If the computational model has 1000 DOFs, there is at least 200 000 iterations of hydrodynamic pressure calculation for each MBD solver iteration. This causes very slow computing speeds and it is a serious issue to be solved.

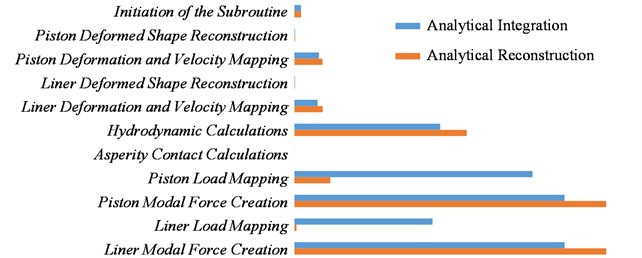
As mentioned above, user-written subroutine is called very often. Therefore, only a slight improvement in the subroutine speed would lead to faster solution times. Looking at the CPU time of hydrodynamic (elastic deformation of piston and liner not considered) analysis with load mapping using analytical integration (blue bars in Fig. 2), it is clear that the load mapping requires the second highest computational times. Therefore, a different approach is proposed – instead of integrating source pressure distribution take its function value at coordinates of target node. One has to be very careful here. Since the static equivalence between source and target of load mapping does not hold anymore, the solver is more unstable – more iterations are needed for converged solution, as it can be seen in the Fig. 2.

If the load mapping by analytical reconstruction is applied in a case of different piston computational grid for lubrication and for deformation, the situation becomes more serious. MBD solver is struggling to converge due to mapping errors. When the overall forces and moments (rigid parts of modal force) from the piston/liner contact are calculated from the source pressure distribution, MBD solver converges successfully once again.

Enabling the deformation of piston and liner changes the biggest contributors of computational time to Piston/Liner Deformed shape Reconstruction (84 % of overall CPU time). More effective approaches to reconstruct piston and liner deformed shape need to be found. Parallel computations could be very helpful, but MBD solver is currently not able to use such technique.

Fig. 2Computational time gain omitting analytical integration during load mapping

2.4. Boundary conditions – oil film height

The text above presents the difficulties in current computational simulation of piston/liner interaction. But what about uncertainties? They can be associated with boundary conditions given to the simulation as an input. Piston and liner true shape (due to the load and temperature) is affecting the piston dynamic behavior very significantly, but these deflections are very hard to obtain, because most of the time they have to be measured in a firing engine.

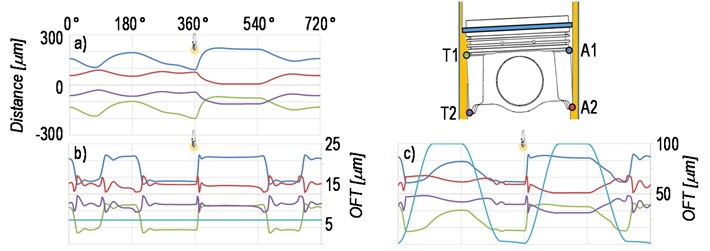
Another source of doubts can be found in the oil film thickness (OFT). What is the oil film thickness distributed to the piston skirt? Fig. 3 compares the piston secondary motion in a case of fully-flooded model, 6 μm model (constant OFT of 6 μm) and hybrid model (in upstroke OFT left by oil-control ring, during downstroke fully-flooded conditions). Offner et al. [6] performed measurements which support the theory of hybrid model of OFT.

Fig. 3Piston secondary motion: a) fully-flooded model, b) 6 μm model, c) hybrid model