Computational simulation of the turbocharger rotor mechanical noise

1. Introduction

Today’s trends as downsizing, downspeeding, exhaust gas turbocharging or engines with a low number of cylinders are modern approaches for the powertrain design. Utilization of turbocharging technology presents effective way how to meet the requested demands. On the other hand, the noise and vibrations increase is evident and it has to be solved by experimental and computational approaches on different system level.

One of the greatest challenges of the turbocharging technology is its very high speed range. Modern turbochargers operate in speed up to the 300 000 min^-1. Turbocharger rotor dynamics and its modelling are historically based on simple linear models, but this solution is not sufficient. A major breakthrough was introduced by Schweizer [1], who used multibody dynamics software (MBS) based tool for turbocharger rotor dynamics prediction. This type of a model is the most commonly used model for turbocharger rotor dynamics simulation. For example, Tian [2] used this type of a model to create a model to study influence of the rotor unbalance and engine vibration on turbocharger rotor dynamics and published the results.

2. Brief theory background

A computational model of the turbocharger rotordynamics is solved in time domain. This enables to incorporate different physical problems, including various nonlinearities. The model is assembled, as well as, numerically solved in multibody system ADAMS. ADAMS is a general code and enables an integration of user-defined models directly using ADAMS commands or using user written FORTRAN or C++ subroutines. The computational model includes all significant components necessary for rotordynamics solution. Rotor shaft, compressor and turbine wheels and hydrodynamics floating bearings are the main parts of the model.

The rotor shaft is modelled by beams using the Euler-Bernoulli non-linear formulation including stress stiffening and spin softening effects. Stress stiffening is the stiffening (or weakening) of a structure due to its stress state. This stiffening effect normally needs to be considered for thin structures with bending stiffness very small compared to axial stiffness, such as cables, thin beams, and shells and couples the in-plane and transverse displacements. This effect also augments the regular nonlinear stiffness matrix produced by large-strain or large-deflection effects. The effect of stress stiffening is accounted for by generating and then using an additional stiffness matrix. The additional stiffness matrix is added to the regular stiffness matrix in order to give the total stiffness. The vibration of a spinning rotor also causes relative circumferential motions, which changes the direction of the centrifugal load which, in turn, will tend to destabilize the structure. As a small deflection analysis cannot directly account for changes in geometry, the effect can be accounted for by an adjustment of the stiffness matrix (spin softening).

The turbocharger rotor incorporates semi floating ring bearing to increase damping effects of common hydrodynamics bearings. Since the journal bearing is represented in the MBS by a set of pre-calculated databases, several presumptions [3] have to be considered to enable creation of the databases in advance. The scheme and general dimensions of fully floating ring bearing is shown in Fig. 2. The bearing consists of three parts – housing bore (sleeve), shaft and floating ring. The floating ring separates shaft from housing bore, and therefore, two oil films are created – inner and outer oil film. Floating ring bearing has three different eccentricities which describe position of floating ring and shaft – overall eccentricity $e$ (between shaft and housing bore), inner eccentricity $e_i$ (between shaft and floating ring) and outer eccentricity $e_o$ (between floating ring and housing bore).

Fig. 1Floating ring bearing model arrangement used: a) Floating ring bearing model scheme, b) Floating ring bearing general dimensions

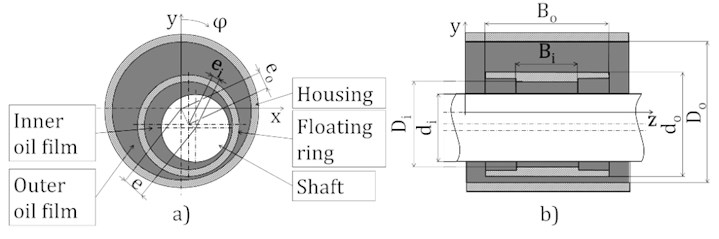
For precise rotor dynamics simulation all bearing parameters have to be known – diameter, width and clearance for both inner and outer oil film, oil parameters – dynamic viscosity, oil input pressure and oil temperature.

Both of the oil films are treated separately as a plain journal bearing. The hydrodynamic pressure and consequential forces and moments are solved numerically by Reynolds equation. The equation is based on the modification of the Navier-Stokes equation and continuity equation transformed for cylindrical shapes of the bearing oil gap. The full form of the equation has been simplified and modified into the following two equations (tangential and radial pin movement) [3]:

where $H$ is dimensionless height of the oil film, $\phi$ is dimensionless angle around pin axis, $Z$ is dimensionless coordinate along bearing width, $D$ is bearing diameter (inner $D_i$ or outer $D_o$ diameter depending on which oil film is modelled), $B$ is bearing width (inner $B_i$ or outer $B_o$ width depending on which oil film is modelled), ${\mathrm{\Pi }}_D$ and ${\mathrm{\Pi }}_V$ are dimensionless pressures and can be calculated as:

where ${\omega }_e$ is effective angular velocity, $\eta$ is dynamic viscosity, $\psi$ is relative bearing clearance and $\dot{\epsilon }$ is derivative of dimensionless pin eccentricity, $p_D$ is pressure due to pin tangential motion and $p_V$ is pressure due to pin radial motion. The definitions of relative parameters are further described in [1].

Eq. (1) describes hydrodynamic pressure formed by tangential movement of the pin and the equation (2) describes hydrodynamic pressure formed by radial movements of the pin.

The Reynolds differential equation is discretised by finite difference method and iteratively solved by Gauss-Seidel method employing successive over-relaxation strategy (SOR). The cavitation condition ensures that the pressure in the oil film is always higher or equal to cavitation pressure. The main parameter that influences distribution of the hydrodynamics pressure is the non-dimensional height of the oil film $H$. The non-dimensional height of the oil film, considering eccentricity and both tilt angles, is shown in equation [4]:

where $\epsilon$ is dimensionless eccentricity (inner or outer eccentricity depending on which oil film is modelled), $\phi$ is dimensionless angle around pin axis, $Z$ is dimensionless coordinate along bearing width and $\gamma$ and $\delta$ are dimensionless journal tilt angles.

The journal bearing model is introduced to the MBS as a set of dimensionless result tables and Eq. (5). The resultant table carries the values of dimensionless forces and torques. This approach enables to solve distribution of the hydrodynamic pressure in advance; and therefore, secure faster solution. To create the hydrodynamic databases, the solver needs diameter to width ratio; every other parameter (e.g. bearing width, diameter and clearance, oil viscosity, etc.) is then entered afterwards into the conversion to the real values of forces and torques:

The symbols $F_{1D}$, $F_{1V}$, $F_{2D}$, $M_{1D}$, $M_{2D}$, $M_{1V}$, are reaction forces and moments in oil film relative to minimal oil film thickness, ${\omega }_e$ is effective angular velocity, $\psi$ is dimensionless clearance and $\mathrm{\Phi }$, $\mathrm{\Theta }$, are dimensionless reaction forces. Index 1 means direction in minimal oil film thickness, index 2 means direction perpendicular to minimal oil film, index $D$ and $V$ mean pressure due to tangential respectively radial pin movement.

Generally, friction moment of the hydrodynamics bearing can be calculated as:

where $R$ is pin radii, $p$ is hydrodynamics pressure, $U$ is surface velocity, $h$ is oil film thickness and $A$ is a bearing area. The Eq. (7) is transferred into dimensionless form as:

The symbols ${\mathrm{\Psi }}_p$ and ${\mathrm{\Psi }}_u$ are dimensionless friction moments.

The dimensionless forces and moments ($\mathrm{\Phi }$, $\mathrm{\Theta }$, $\mathrm{\Psi }$) are stored in hydrodynamics databases and they are read during dynamics solution. The transition to the dimensionless form enables to solve the equation effectively and also to solve the equation for groups of bearing (depending only on $D/B$ ratio).

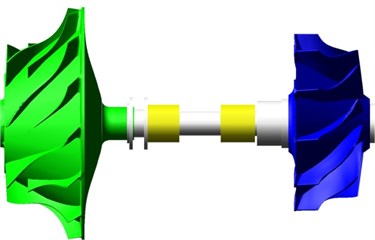
A geometric visualisation of the turbocharger rotor in Multibody dynamic software is presented in Fig. 2.

Fig. 2Multibody dynamics model of turbocharger rotor

3. Examples of vibrational results

The proposed computational model enables to calculate a wide range of results. Rotor dynamics is one of important results if the noise and vibrations are in concern. The inner and outer bearing eccentricities on the turbine and compressor sides are presented in Fig. 3. It can be clearly seen, that the eccentricity shows high peak near engine speed of 30 000 min^-1, because of the rotor passing the first bending frequency.

Fig. 3Relative eccentricities of bearings

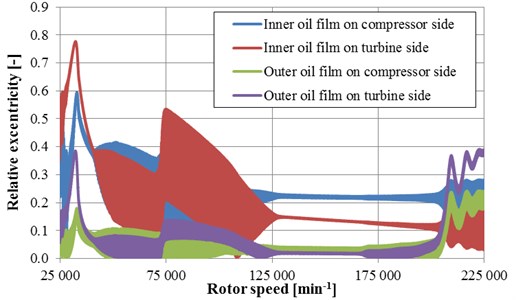
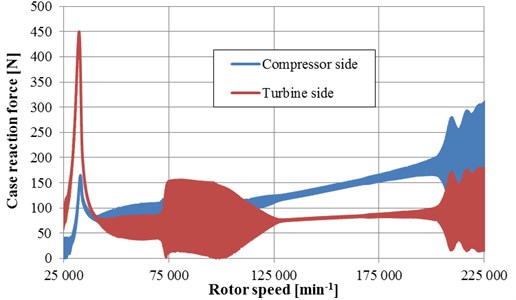
Fig. 4Reacting forces into the rotor case on compressor and turbine sides

The eccentricity increase around engine speed of 75 000 min^-1 is connected to an instability of inner oil film (oil whirl) and eccentricity increase around engine speed of 200 000 min^-1 is connected to an instability of outer oil film (oil whirl).

It is very important to mention, there are some input parameters influencing the rotor dynamics and these have to be considered. Rotor unbalance, bearing clearances and angle positions of unbalances are very important to correctly set-up.

A generation of structural borne noise can be estimated from reacting forces into the rotor case on compressor and turbine side (see Fig. 4). Because of high rotor speeds, large unbalancing forces occur in turbocharger systems. These rotating forces are linearly proportional to the frequency of the rotor speed and cause a tonal noise, commonly known as unbalancing whistle. The rotor unbalance is the main noise source in this case of rotor set-up.

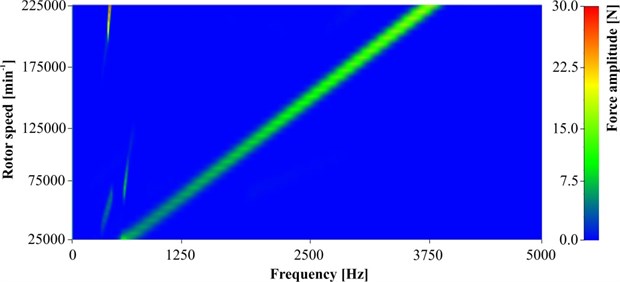
The cause of the increase of unbalancing whistle can be seen in the contour plot in Fig. 5, presenting force amplitude on compressor side bearing vs. frequency and rotor speed.

Fig. 5Contour plot of reacting force into the rotor case on compressor side

4. Conclusions

The efficient and robust computational model for a solution of turbocharger rotor dynamics including fully floating bearing is introduced in the paper. The effective solution in the time domain enabling transient nonlinear solution of rotor dynamic and bearing tribology is one of the main benefits. There are much more parameters that can be included into the results. Oil temperature, input oil pressure or oil flow are such a parameter with high impact on rotor dynamics and mechanical losses.