Mathematical model of elastic ribbed shell dynamics interaction with viscous liquid under vibration

Kondratov, Dmitry V.; Kalinina, Anna V.; Mogilevich, Lev I.; Popova, Anna A.; Kondratova, Yulia N.

Vibroengineering Procedia

Browse Procedia

Published: 07 October 2016

Check for updates

Mathematical model of elastic ribbed shell dynamics interaction with viscous liquid under vibration

Dmitry V. Kondratov¹

Anna V. Kalinina²

Lev I. Mogilevich³

Anna A. Popova⁴

Yulia N. Kondratova⁵

^{1, 2}Russian Presidential Academy of National Economy and Public Administration, Saratov, Russian Federation

^{3, 4}Yuri Gagarin State Technical University of Saratov, Saratov, Russian Federation

⁵Saratov State University, Saratov, Russian Federation

Corresponding Author:

Dmitry V. Kondratov

Cite the article Download PDF

Downloads 1304

Abstract

The mechanical model of the system, formed by two surfaces of the coaxial cylindrical shells interacting with viscous incompressible liquid between them under vibration, is considered. The outer shell is geometrically irregular, and inner one is an absolutely rigid cylinder. The mathematical model of this system, consisting of differential equations in partial derivatives for describing dynamics of viscous incompressible liquid and an elastic ribbed shell together with boundary conditions is constructed. The expressions for amplitude frequency characteristics of outer geometrically irregular shell are discovered.

1. Introduction

The pipelines are one of the basic elements in modern devices and various engineering constructions applied in aviation. Such devices are represented by pipelines of the hydraulic drive, cooling, greasing, fuel supply, dosaging system, power cylinder and ram-type pairs [1]. The studies of the mechanical systems, consisting of coaxial geometrically regular cylindrical shells with pressure pulsations or under vibrations were conducted earlier [2-8].

The present paper considers the pipeline system of ring like profile with elastic geometrically irregular outer shell of final length and absolutely rigid inner cylinder, interacting with viscous incompressible liquid between them under vibration for defining and regulating oscillations of “shell-fluid” system.

It should be noted that this problem is relevant because real mechanical systems are constantly exposed to different vibration impacts from both external and internal sources. Vibration leads to emerging substantial oscillations of pipeline systems. At resonance frequencies the walls velocities of the pipeline elastic shells will be maximum, and it can lead to ruptures in a fluid and emergence of vibrational cavitation. Gas bubbles bursting on walls, lead to pipeline walls damage and therefore to cavitation wear [9].

2. Statement of the problem

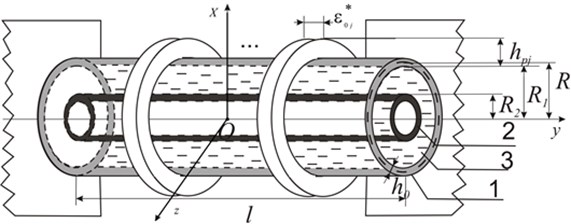
Let us consider the mechanical model presented on Fig. 1.

The outer shell is an elastic cylindrical geometrically irregular shell. The inner shell can be considered as absolutely rigid cylinder. Viscous incompressible liquid is placed between the indicated cylindrical shells. The radius of outer ribbed shell medium surface equals $R$ , and its thickness at the places, without rigid ribs equals $h_{0}$ . The length of cylindrical shells $l$ are equal, and elastic shifts of an outer ribbed shell are much less than the width $δ$ of the cylindrical slot. The width $δ = R_{1} - R_{2} ≪ R_{2}$ of the ring crossed section cylindrical slot, formed by two shells, is less than outer radius $R_{2}$ of the inner shell and inner radius $R_{1}$ of an outer shell. The medium surface radius $R$ is much larger than the width of an outer shell $h_{0}^{} = 2 (R - R_{1})$ . The temperature effects in the system discussed above are not considered.

In the present mechanical model we will determine amplitude-frequency characteristic of outer geometrically irregular shell sagging.

Fig. 1The mechanical model

3. The theory

The movements of viscous incompressible liquid in coordinate system $r$ , $θ$ , $y$ rigidly connected with the center of coordinates, are presented by Navier-Stokes equations and by continuity equation for an axes symmetric case in a scalar state [10, 11]:

1

W_{r} = - \frac{1}{ρ} \frac{\partial p}{\partial r} + ν (\frac{\partial^{2} V_{r}}{\partial r^{2}} + \frac{1}{r} \frac{\partial V_{r}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} V_{r}}{\partial θ^{2}} + \frac{\partial^{2} V_{r}}{\partial y^{2}} - \frac{2}{r^{2}} \frac{\partial V_{θ}}{\partial θ} - \frac{V_{r}}{r^{2}}),

W_{θ} = - \frac{1}{ρ r} \frac{\partial p}{\partial θ} + ν (\frac{\partial^{2} V_{θ}}{\partial r^{2}} + \frac{1}{r} \frac{\partial V_{θ}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} V_{θ}}{\partial θ^{2}} + \frac{\partial^{2} V_{θ}}{\partial y^{2}} + \frac{2}{r^{2}} \frac{\partial V_{r}}{\partial θ} - \frac{V_{θ}}{r^{2}}),

W_{y} = - \frac{1}{ρ} \frac{\partial p}{\partial y} + ν (\frac{\partial^{2} V_{y}}{\partial r^{2}} + \frac{1}{r} \frac{\partial V_{y}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} V_{y}}{\partial θ^{2}} + \frac{\partial^{2} V_{y}}{\partial y^{2}}),

\frac{\partial V_{r}}{\partial r} + \frac{V_{r}}{r} + \frac{1}{r} \frac{\partial V_{θ}}{\partial θ} + \frac{\partial V_{y}}{\partial y} = 0,

where:

W_{r} = W_{1 z 1} c o s θ + W_{1 x 1} s i n θ + \frac{\partial V_{r}}{\partial t} + V_{r} \frac{\partial V_{r}}{\partial r} + \frac{V_{θ} \partial V_{r}}{r \partial θ} + V_{y} \frac{\partial V_{r}}{\partial y} - \frac{V_{θ}^{2}}{r},

W_{θ} = - W_{1 z 1} s i n θ + W_{1 x 1} c o s θ + \frac{\partial V_{θ}}{\partial t} + V_{r} \frac{\partial V_{θ}}{\partial r} + \frac{V_{θ}}{r} \frac{\partial V_{θ}}{\partial θ} + V_{y} \frac{\partial V_{θ}}{\partial y} + \frac{V_{r} V_{θ}}{r},

W_{y} = \frac{\partial V_{y}}{\partial t} + V_{r} \frac{\partial V_{y}}{\partial r} + \frac{V_{θ}}{r} \frac{\partial V_{y}}{\partial θ} + V_{y} \frac{\partial V_{y}}{\partial y},

where $p$ – pressure of viscous incompressible liquid; $V_{y}$ , $V_{r}$ , $V_{θ}$ – are the components of liquid velocity vector $({\bar{n}}_{r}, \bar{j})$ in which the beginning is located in the center of the inner shell $O$ ; $t$ – time; $ν$ – kinematic coefficient of viscosity; $r$ – distance from an axis $O y$ ; $ρ$ – liquid density, $W_{1 x 1} = E_{x} ω^{2} s i n (ω t)$ , $W_{1 z 1} = E_{z} ω^{2} s i n (ω t)$ – vibroacceleration of a base which is attached to a mechanical system into inertial space.

The boundary conditions for cylindrical axes on impenetrable surface of outer and inner shells in a cylindrical clearance for Eq. (1) are:

2

V_{r} = \frac{\partial u_{3}^{}}{\partial t}, V_{θ} = \frac{\partial u_{2}^{}}{\partial t}, V_{y} = \frac{- \partial u_{1}^{}}{\partial t} at r = R_{2} + δ + u_{3}^{`},

V_{r} = 0, V_{θ} = 0, V_{y} = 0 at r = R_{2},

where $u_{1}^{} = u_{1}^{} (y, θ, t)$ – elastic longitudinal shell shift which is positive in the direction ${\bar{n}}_{s}$ , opposite in the direction $\bar{j}$ ; $u_{2}^{} = u_{2}^{} (y, θ, t)$ – circumferential elastic movement in the direction ${\bar{n}}_{θ}$ , $u_{3}^{} = u_{3}^{} (y, θ, t)$ –shell sagging which is positive in the direction $\bar{n}$ , coinciding with ${\bar{n}}_{r}$ and opposite in a direction to a curvature center; $\bar{u} = u_{1} {\bar{n}}_{s} + u_{2} {\bar{n}}_{θ} + u_{3} \bar{n}$ – vector displacement of the elastic shell.

The outer surface of a pipe outer shell represents geometrically irregular shell, having n of rigidity ribs which altitude changes stepwise. The ribs present outer frames. The strengthening of geometrically irregular shell at butt ends has free attaching [11].

The dynamic equations of a ribbed shell based on Kirchhoff-Love hypotheses, proceeding from the received Hamilton integral variational principle, in cylindrical axes are:

3

\frac{\partial}{\partial y} (\frac{E h_{0}}{1 - μ_{0}^{2}} \{[- \frac{\partial u_{1}}{\partial y} + μ_{0} \frac{1}{R} (\frac{\partial u_{2}}{\partial θ} + u_{3})] \cdot k_{1} (y)

+ (μ_{0} \frac{1}{R^{2}} (\frac{\partial u_{2}}{\partial θ} - \frac{\partial^{2} u_{3}}{\partial θ^{2}}) - \frac{\partial^{2} u_{3}}{\partial y^{2}}) \cdot h_{0} k_{2} (y\}) + \frac{1}{R} \frac{\partial}{\partial θ} (\frac{E h_{0}}{2 (1 + μ_{0})} \{(\frac{\partial u_{2}}{\partial y} - \frac{1}{R} \frac{\partial u_{1}}{\partial θ}) \cdot k_{1} (y)

+ \frac{2}{R} (\frac{\partial u_{2}}{\partial y} - \frac{\partial^{2} u_{3}}{\partial y \partial θ}) \cdot h_{0} k_{2} (y)\}) = - h_{0} ρ_{0} \frac{\partial^{2} u_{1}}{\partial t^{2}} k_{1} (y) - q_{s},

\frac{\partial}{\partial y} (\frac{E h_{0}}{2 (1 + μ_{0})} \{(\frac{\partial u_{2}}{\partial y} - \frac{1}{R} \frac{\partial u_{1}}{\partial θ}) \cdot k_{1} (y) + \frac{2}{R} (\frac{\partial u_{2}}{\partial y} - \frac{\partial^{2} u_{3}}{\partial y \partial θ}) \cdot h_{0} k_{2} (y)\})

+ \frac{1}{R} \frac{\partial}{\partial θ} (\frac{E h_{0}}{1 - μ_{0}^{2}} \{(\frac{1}{R} (\frac{\partial u_{2}}{\partial θ} + u_{3}) - μ_{0} \frac{\partial u_{1}}{\partial y}) k_{1} (y)

+ (\frac{1}{R^{2}} (\frac{\partial u_{2}}{\partial θ} - \frac{\partial^{2} u_{3}}{\partial θ^{2}}) - μ_{0} \frac{\partial^{2} u_{3}}{\partial y^{2}}) h_{0} k_{2} (y)\})

+ \frac{1}{R^{2}} \frac{\partial}{\partial θ} (\frac{E h_{0}^{3}}{12 (1 + {μ_{0}}^{2})} (\frac{1}{R^{2}} (\frac{\partial u_{2}}{\partial θ} - \frac{\partial^{2} u_{3}}{\partial θ^{2}}) - μ_{0} \frac{\partial^{2} u_{3}}{\partial y^{2}}) k_{3} (y)

+ \frac{E h_{0}}{1 - μ_{0}^{2}} (- μ_{0} \frac{\partial u_{1}}{\partial y} + \frac{1}{R} (\frac{\partial u_{2}}{\partial θ} + u_{3})) \cdot h_{0} k_{2} (y))

+ \frac{2}{R} \frac{\partial}{\partial y} (\frac{E h_{0}^{3}}{12 (1 + μ_{0})} \frac{1}{R} (\frac{\partial u_{2}}{\partial y} - \frac{\partial^{2} u_{3}}{\partial y \partial θ}) k_{3} (y) + \frac{E h_{0}}{2 (1 + μ_{0})} (\frac{\partial u_{2}}{\partial y} - \frac{1}{R} \frac{\partial u_{1}}{\partial θ}) \cdot h_{0} k_{2} (y))

= h_{0} ρ_{0} (W_{1 x 1} s i n θ - W_{1 z 1} c o s θ \frac{\partial^{2} u_{2}}{\partial t^{2}}) k_{1} (y) - q_{θ},

\frac{\partial^{2}}{\partial y^{2}} (\frac{E h_{0}^{3}}{12 (1 - {μ_{0}}^{2})} (μ_{0} \frac{1}{R^{2}} (\frac{\partial u_{2}}{\partial θ} - \frac{\partial^{2} u_{3}}{\partial θ^{2}}) - \frac{\partial^{2} u_{3}}{\partial y^{2}}) k_{3} (y)

+ \frac{E h_{0}}{1 - μ_{0}^{2}} (\frac{\partial u_{1}}{\partial y} + μ_{0} \frac{1}{R} (\frac{\partial u_{1}}{\partial θ} + u_{3})) h_{0} k_{2} (y))

+ \frac{1}{R^{2}} \frac{\partial^{2}}{\partial θ^{2}} (\frac{E h_{0}^{3}}{12 (1 - {μ_{0}}^{2})} (\frac{1}{R^{2}} (\frac{\partial u_{2}}{\partial θ} - \frac{\partial^{2} u_{3}}{\partial θ^{2}}) - μ_{0} \frac{\partial^{2} u_{3}}{\partial y^{2}}) k_{3} (y)

+ \frac{E h_{0}}{1 - μ_{0}^{2}} (- μ_{0} \frac{\partial u_{1}}{\partial y} + \frac{1}{R} (\frac{\partial u_{2}}{\partial θ} + u_{3})) \cdot h_{0} k_{2} (y))

+ \frac{2}{R} \frac{\partial}{\partial θ \partial y} (\frac{E h_{0}^{3}}{12 (1 + μ_{0})} \frac{1}{R} (\frac{\partial u_{2}}{\partial y} - \frac{\partial^{2} u_{3}}{\partial y \partial θ}) k_{3} (y)

+ \frac{E h_{0}}{2 (1 + μ_{0})} (\frac{\partial u_{2}}{\partial y} - \frac{1}{R} \frac{\partial u_{1}}{\partial θ}) \cdot h_{0} k_{2} (y)) - \frac{1}{R} (\frac{E h_{0}}{1 - μ_{0}^{2}} \{(\frac{1}{R} (\frac{\partial u_{2}}{\partial θ} + u_{3}) - μ_{0} \frac{\partial u_{1}}{\partial y}) k_{1} (y)

+ (\frac{1}{R^{2}} (\frac{\partial u_{2}}{\partial θ} - \frac{\partial^{2} u_{3}}{\partial θ^{2}}) - μ_{0} \frac{\partial^{2} u_{3}}{\partial y^{2}}) h_{0} k_{2} (y)\})

= - h_{0} ρ_{0} (W_{1 x 1} s i n θ + W_{1 z 1} c o s θ + \frac{\partial^{2} u_{3}}{\partial t^{2}}) k_{1} (y) - q_{n},

where:

k_{1 j} = (1 - \frac{h_{0}}{h_{p j}}) \frac{h_{p j}}{h_{0}}, k_{2 j} = (1 - \frac{h_{0}}{h_{p j}}) \frac{h_{p j}^{2}}{2 h_{0}^{2}}, k_{3 j} = (1 - \frac{h_{0}}{h_{p j}}) (4 - 2 \frac{h_{0}}{h_{p j}} + \frac{h_{0}^{2}}{h_{p j}^{2}}) \frac{h_{p j}^{3}}{h_{0}^{3}} .

$Δ Γ_{y j} = Γ (y - y_{j}) - Γ (y - y_{j} - ε_{0 j}^{*})$ , $Γ (y)$ – is a unit function Heaviside on the longitudinal coordinate $y$ ; $μ_{0}$ – Poisson’s ratio of shell material; $y_{j}$ – is a point, where the rib appears on the longitudinal coordinate; $ρ_{0}$ – shell material density; $E$ – shell material Young modulus:

4

q_{s}^{} = - [P_{r y}^{} c o s^{} (\bar{n}, {\bar{n}}_{r}) + P_{θ y}^{} c o s^{} (\bar{n}, {\bar{n}}_{θ}) + P_{y y}^{} c o s^{} (\bar{n}, \bar{j})] |_{r = r^{(1)}},

q_{θ}^{} = [P_{r θ}^{} c o s^{} (\bar{n}, {\bar{n}}_{r}) + P_{θ θ}^{} c o s^{} (\bar{n}, {\bar{n}}_{θ}) + P_{θ y}^{} c o s (\bar{n}, \bar{j})] |_{r = r^{(1)}},

q_{n}^{} = [P_{r r}^{} c o s^{} (\bar{n}, {\bar{n}}_{r}) + P_{r θ}^{} c o s^{} (\bar{n}, {\bar{n}}_{θ}) + P_{r y}^{} c o s^{(i)} (\bar{n}, \bar{j})] |_{r = r^{(1)}},

r^{(1)} = R_{2} + δ + u_{3}^{}, P_{r r} = - p + 2 ρ ν \frac{\partial V_{r}}{\partial r}, P_{r θ} = ρ ν (\frac{\partial V_{θ}}{\partial r} - \frac{V_{θ}}{r} + \frac{1}{r} \frac{\partial V_{r}}{\partial θ}),

P_{θ θ} = - p + 2 ρ ν (\frac{1}{r} \frac{\partial V_{θ}}{\partial θ} + \frac{V_{r}}{r}), P_{r y} = ρ ν (\frac{\partial V_{y}}{\partial r} + \frac{\partial V_{r}}{\partial y}), P_{y y} = - p + 2 ρ ν \frac{\partial V_{y}}{\partial y},

P_{θ y} = ρ ν (\frac{\partial V_{θ}}{\partial y} + \frac{1}{r} \frac{\partial V_{y}}{\partial θ}), c o s^{} (\bar{n}, {\bar{n}}_{r}) = \frac{r}{|\bar{N}|}, c o s (\bar{n}, {\bar{n}}_{θ}) = - \frac{1}{|\bar{N}|} \frac{\partial u_{3}^{}}{\partial θ},

c o s (\bar{n}, \bar{j}) = - \frac{r}{|\bar{N}|} \frac{\partial u_{3}^{}}{\partial y}, |\bar{N}| = {\{r^{2} {[1 + \frac{\partial u_{3}^{}}{\partial y}]}^{2} + {(\frac{\partial u_{3}^{}}{\partial θ})}^{2}\}}^{\frac{1}{2}}, {(a_{0}^{})}^{2} = \frac{{(h_{0}^{})}^{2}}{12 R^{2}} .

The boundary conditions of outer geometrically irregular shell free attaching look like:

5

\frac{\partial u_{1}^{}}{\partial y} = 0, u_{2}^{} = 0, u_{3}^{} = 0, \frac{\partial^{2} u_{3}^{}}{\partial y^{2}} = 0 at y = \pm \frac{l}{2} .

The bound hydroelasticity problem Eq. (1-5) is solved in the undimensional variables by perturbation method [12-15] with the use of two small parameters describing the relative width of liquid layer and relative outer elastic geometrically irregular shell sagging by presupposing the harmonic law of system vibration. Such approach allows linearizing the problem of fluid dynamics. Liquid movements velocity and pressure in liquid layer, received in the course of hydrodynamics equations solution, allow to find the stresses acting on the shell. They are substituted in elastic geometrically irregular cylindrical shell dynamic equations. As a result, the system of integrodifferential equations is received.

Bubnov-Galerkin method in the longitudinal coordinate is applied to the solution of integrodifferential equations system [11, 15], where elastic shells movements are presented as trigonometric series in $ζ$ and harmonic function in $θ$ :

6

u_{1}^{} = u_{m}^{} U_{1}^{} = u_{m}^{} \sum_{k = 1}^{\infty} s i n (\frac{2 k - 1}{2} π ζ) \{(a_{10 C}^{} c o s θ + a_{10 S}^{} s i n θ) s i n (τ + φ_{u 1}^{}) + a_{10 O}^{}\},

u_{2}^{} = v_{m}^{} U_{2}^{} = v_{m}^{} \sum_{k = 1}^{\infty} c o s (\frac{2 k - 1}{2} π ζ) \{a_{20 S}^{} c o s θ + a_{20 C}^{} s i n θ + a_{20 O}^{}\} s i n (τ + φ_{u 2}^{}),

u_{3}^{} = w_{m}^{} U_{3}^{} = w_{m} \sum_{k = 1}^{\infty} c o s (\frac{2 k - 1}{2} π ζ) \{(a_{30 C}^{} c o s θ + a_{30 S}^{} s i n θ) s i n (τ + φ_{u 3}^{}) + a_{30 O}^{}\} .

Thus, as a result of the solution of hydroelasticity problem, we shall get the expressions for outer elastic ribbed shell elastic shifts.

It was shown earlier that for the study of the resonance amplitude-frequency characteristic in solving the equations of the dynamics of the shell it is sufficient to take only the first term of the series Eq. (6) [16].

By solving the considered system of simple equations, we get new coefficients in the expressions of outer geometrically irregular shell sagging, which in the dimensional state will become:

7

u_{30}^{} = c o s (\frac{π ζ}{2}) (a_{30 O}^{} + \sqrt{\frac{A n}{D n}} \times (\begin{matrix} E_{z} ω^{2} c o s θ s i n (ω t + φ_{z 0} + η (ω)) \\ + E_{x} ω^{2} s i n θ s i n (ω t + φ_{x 0} + η (ω)) \end{matrix})) .

We get the corresponding matching amplitude-frequency characteristic of outer shell sagging:

8

A (ω) = \sqrt{\frac{A n}{D n}},

where $A n$ , $D n$ – expression system-dependent parameters are not discussed here due to where cumbersomeness; $η (ω)$ – phase frequency characteristic.

4. Conclusions

Thus, the mathematical model of the mechanical system consisting of two coaxial cylindrical shells of final length, with the free attaching at butt ends is constructed. The outer shell is geometrically irregular, and the inner one is an absolutely rigid cylinder. The mechanical system is exposed to vibration. Such model of the system considers the liquid movement inertias and elasticity of final length outer shell, having rigid ribs. The constructed model allowed to define the expressions for outer geometrically irregular shell amplitude frequency characteristics. The proposed model allows to choose optimal parameters, proceeding from the known frequency range of vibration and necessary parameters of wear hardness, at the stage of mechanisms projects.

References

Bashta T. M. Mashinostroitel’naya Gidravlika (Engineering Hydraulics). Mashinostroenie, Moscow, 1971, (in Russian).

Search CrossRef
Slezkin N. A. Dinamika Viazkoi Neszhimaemoi Zhidkosti (Dynamics of a Viscous Incompressible Fluid). Gostekhizdat, Moscow, 1955, (in Russian).

Search CrossRef
Womersley J. R. Oscillatory motion of a viscous liquid in a thin-walled elastic tube. Part 1: the linear approximation for long waves. Philosophical Magazine, Vol. 46, 1955, p. 199-221.

Search CrossRef
Kondratov D. V., Kondratova J. N., Mogilevich L. I., Rabinsky L. N., Kuznetsova E. L. Mathematical model of elastic ribbed shell dynamics interaction with viscous liquid pulsating layer. Applied Mathematical Sciences, Vol. 9, Issues 69-72, 2015, p. 3525-3531.

Search CrossRef
Kondratov D. V., Kondratova J. N., Mogilevich L. I. Oscillating laminar fluid flow in a cylindrical elastic pipe of annular cross-section. Fluid Dynamics, Vol. 44, Issue 2009, 4, p. 528-539.

Search CrossRef
Antsiferov S. A., Kondratov D. V., Mogilevich L. I. Perturbing moments in a floating gyroscope with elastic device housing on a vibrating base in the case of a nonsymmetric end outflow. Mechanics of Solids, Vol. 44, Issue 3, 2009, p. 352-360.

Search CrossRef
Kondratov D. V., Kondratova J. N., Mogilevich L. I. Studies of the amplitude frequency characteristics of oscillations of the tube elastic walls of a circular profile during pulsed motion of a viscous fluid under the conditions of rigid jamming on the butt-ends. Journal of Machinery Manufacture and Reliability, Vol. 38, Issue 3, 2009, p. 229-234.

Search CrossRef
Gorshkov A. G., Medvedsky A. L., Rabinsky L. N., Tarlakovsky D. V. Volni v Sploshnikh Sredakh (Waves in Continuous Mediums). Fizmatlit, 2004, (in Russian).

Search CrossRef
Ivanchenko N. N., Skuridin A. A., Nikitin M. D. Kavitatsionnoe Razrushenie v Dizelyakh (Cavitation Destruction in Diesel Motors), Mashinostroenie, Leningrad, 1970, (in Russian).

Search CrossRef
Loitsyanskii L. G. Mechanics of Liquids and Gases. Pergamon Press, Oxford, 1966.

Search CrossRef
Kondratov D. V., Plaksina I. V. Hydroelasticity Geometrically Irregular Shell Containing the Stratum of the Viscous Liquid and Absolutely Rigid Cylinder, in Conditions of Harmonic Pressure. Modern Scientific Research and Their Practical Application. Kupriyenko SV, Odessa, 2013

Search CrossRef
van Dyke M. Perturbation Methods in Fluid Mechanics. The Parabolic Press, Stanford, CA, 1975.

Search CrossRef
Ageev R. V., Mogilevich L. I., Popov V. S., Popova A. A., Kondratov D. V. Mathematical model of pulsating viscous liquid layer movement in a flat channel with elastically fixed wall. Applied Mathematical Sciences, Vol. 8, Issue 2014, 159, p. 7899-7908.

Search CrossRef
Mogilevich L. I., Popov V. S. Investigation of the interaction between a viscous incompressible fluid layer and walls of a channel formed by coaxial vibrating discs. Fluid Dynamics, Vol. 46, Issue 3, 2011, p. 375-388.

Search CrossRef
Kondratov D. V., Kalinina A. V. Examination of processes of a hydroelasticity of a ridge pipe ring a lateral view at action of vibration. Journal “Trudy MAI”, Vol. 78, 2014, (in Russian).

Search CrossRef
Kalinina A. V., Kondratov D. V., Kondratova J. N., Plaksina I. V., Kuznetsova E. L. Mathematical modelling of hydroelasticity processes ribbed pipe of ring like profile at pressure pulsating. Izvestija Tulskogo Gosudarstvennogo Universiteta, Technicheskie Nauki, Vol. 7, Issue 1, 2015, p. 40-55, (in Russian).

Search CrossRef

About this article

Received

08 June 2016

Accepted

24 August 2016

Published

07 October 2016

SUBJECTS

Flow induced structural vibrations

Keywords

mathematical modeling

hydroelasticity

viscous liquid

coaxial cylindrical shells

geometrically irregular shell

vibration

Acknowledgements

The research is made under the financial support of RFFI Grants No. 15-01-01604-а, No. 16-01-00175-а and President of Russian Federation Grant No. MD-6012.2016.8.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.