Bending oscillations of a cylinder, surrounded by an elastic medium and containing a viscous liquid and an oscillator

Mogilevich, Lev I.; Popov, Victor S.; Kondratov, Dmitry V.; Rabinskiy, Lev N.

doi:10.21595/jve.2017.18179

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 December 2017

Check for updates

Bending oscillations of a cylinder, surrounded by an elastic medium and containing a viscous liquid and an oscillator

Lev I. Mogilevich¹

Victor S. Popov²

Dmitry V. Kondratov³

Lev N. Rabinskiy⁴

^{1, 2}Yuri Gagarin State Technical University of Saratov, Saratov, Russia

³Russian Presidential Academy of National Economy and Public Administration, Saratov, Russia

⁴Moscow Aviation Institute (National Research University), Moscow, Russia

Corresponding Author:

Victor S. Popov

Cite the article Download PDF

Downloads 1565

WoS Core Citations 1

CrossRef Citations 6

Abstract

The article considers dynamic processes mathematical modeling in a mechanical system, consisting of an elastic hollow cylinder, surrounded by an elastic medium and containing viscous liquid and vibrating coaxial rigid cylinder. The amplitude frequency characteristic for investigating bending cylinder oscillations as one-mass system is defined. It is shown, that the constructed amplitude characteristic makes it possible to define the considered system resonance frequencies oscillations. The calculations demonstrated the significance of taking into account viscous liquid inertia and the surrounding elastic medium.

1. Introduction

The problems of mathematical modeling of elastic construction elements interaction with liquid are of theoretical and practical interest [1]. For example, [2-8] deal with hydroelasticity problems of homogeneous plates, interacting with viscous liquid layer in various settings. Reference [9] considers the bending oscillations of a flat channel wall, interacting with pulsating viscous liquid. References [10-12] investigate the hydroelastic oscillations of three-layered plates, interacting with viscous pulsating liquid, as well as under inertial excitation. References [13-18] research in the axis-symmetric problem of geometrically regular and ribbed cylinder shells, as well as the ones, forming an annular channel. The non-linear longitudinal deformation wave propagation in cylinder shells, filled with viscous liquid and in axis-symmetric setting is presented in [19, 20]. Reference [21] considers membrane oscillations on an elastic foundation on the pool bottom, the pool being filled with an ideal incompressible liquid with a free surface. References [22, 23] are devoted to the plate oscillation investigation, the plate standing on the elastic foundation and interacting with viscous liquid layer.

However, mathematical modeling of hydroelastic oscillations of a hollow cylinder, surrounded by an elastic medium and containing a viscous liquid and an oscillator, remained beyond the framework of the sources, mentioned above. Therefore, the problem under consideration is of undoubted interest for the research.

2. Mathematical formulation

Let us consider an elastic hollow cylinder, surrounded by an elastic medium (Fig. 1). The cylinder length is $l$ , its thickness $h_{0}$ is significantly less than inner radius $R_{1}$ . The elastic cylinder is simply supported at its edges. The rigid cylinder with radius $R$ is inside the elastic cylinder, mentioned above. The inner and outer cylinders surfaces are parallel to each other. The radial clearance between the cylinders is filled with viscous incompressible liquid. The seals, hindering the liquid leakage out of radial clearance, are supposed to exist on the edges. The rigid cylinder produces harmonic oscillations according to the set law in the plane, being normal to its axis. The hollow cylinder, surrounded by elastic medium, makes bending oscillations, caused by inner cylinder vibrations. Cylinders oscillations amplitudes are considerably less, than liquid layer thickness $δ$ . The elastic medium, surrounding the inner cylinder, can be considered as Winkler foundation.

Fig. 1A schematic diagram of an elastic hollow cylinder, surrounded by an elastic medium and containing viscous liquid and vibrating coaxial rigid cylinder

A schematic diagram of an elastic hollow cylinder, surrounded by an elastic medium and containing viscous liquid and vibrating coaxial rigid cylinder

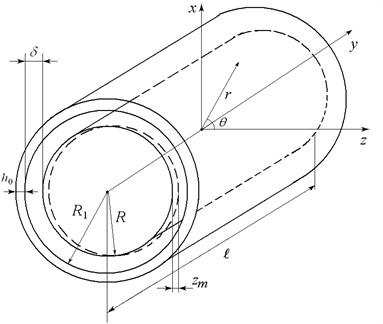
Let us introduce Cartesian coordinate system $x y z$ and cylindrical coordinate system $r θ y$ . We place coordinate systems centers in inner cylinder geometric centre in unperturbed state.

The absolute rigid cylinder displacement law has the form of:

1

z = z_{m} f (ω t), f (ω t) = s i n ω t,

where $z_{m}$ is the rigid cylinder oscillations amplitude, $ω$ is the frequency, $t$ is the time.

The damping at the expense of viscous incompressible liquid is present in the considered oscillation system. As result, transient processes will go out in the course of time. That is why, we will restrict to the consideration the stationary harmonic oscillations study [24].

In accordance with the approach, suggested in [18], we study the deflection of a hollow cylinder, surrounded by an elastic medium, by means of one-mass system. In so doing we consider it in the form of a hollow rigid cylinder with equivalent mass $m^{*}$ and an elastic connection with equivalent stiffness coefficient $n$ . We find the equivalent mass $m^{*}$ under the condition of distributed and one-mass systems kinematic energy coincidence, the equivalent stiffness coefficient $n$ being defined by means of hollow cylinder maximal deflection $w_{m a x}$ under uniform loading, equivalent to one Newton force (i.e. $F^{*} =$ 1 N):

2

m^{*} = (w_{a})^{- 2} \int_{- l / 2}^{l / 2} m_{c} w^{2} d y, n = \frac{F^{*}}{w_{m a x}} .

Here $w$ is the hollow cylinder deflection form function, $w_{a}$ is the hollow cylinder deflection function value at the mass concentration point of one-mass system, $m_{c}$ is the distributed mass per hollow cylinder length unit.

Let us choose the bending oscillations form to be sufficiently close to the expected one and satisfying the boundary conditions at the edges. The deflection of an annular cross section beam, based on Winkler foundation under the uniformly distributed load is chosen as such a form. To define this deflection, we present it in the form of a trigonometric series by longitudinal coordinate, limited by its first member. By taking into account that the equivalent mass is concentrated in the centre (i.e. at the point $y =$ 0), we obtain:

3

m^{*} = ρ_{0} π l h_{0} (R_{1} + \frac{h_{0}}{2}), n = \frac{E J π^{5}}{4 l^{3}} (1 + \frac{k}{E J} \frac{l^{4}}{π^{4}}), J = \frac{π ((R_{1} + h_{0})^{4} - {R_{1}}^{4})}{4},

where $ρ_{0}$ is the hollow cylinder material density, $J$ is the moment of inertia of hollow cylinder-beam cross-section, $E$ is the Young’s modulus of outer cylinder material, $k$ is the elastic coefficient of Winkler foundation.

The transition to one-mass system allows to write down the hollow cylinder motion equation in the form of:

4

m^{*} {\ddot{z}}_{1} + n z_{1} = N, N = \int_{0}^{2 π} \int_{- l / 2}^{l / 2} p c o s (θ) R_{1} d θ d y,

where $N$ is the force, acting on the hollow cylinder from liquid; $z_{1} = z_{1 m} f_{1} (ω t)$ is the displacement law of hollow cylinder, surrounded by elastic medium (within the frameworks of one-mass model); $p$ is the liquid pressure.

Viscous incompressible liquid dynamic equations, presented by Navier-Stocks equations and continuity equation, as well [25] have the form of:

5

\frac{\partial V_{r}}{\partial t} + V_{r} \frac{\partial V_{r}}{\partial r} + \frac{V_{θ}}{r} \frac{\partial V_{r}}{\partial θ} + V_{y} \frac{\partial V_{r}}{\partial y} - \frac{V_{θ}^{2}}{r}

= - \frac{1}{ρ} \frac{\partial p}{\partial r} + ν (\frac{\partial^{2} V_{r}}{\partial r^{2}} + \frac{1}{r} \frac{\partial V_{r}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} V_{r}}{\partial θ^{2}} + \frac{\partial^{2} V_{r}}{\partial y^{2}} - \frac{2}{r^{2}} \frac{\partial V_{θ}}{\partial θ} - \frac{V_{r}}{r^{2}}),

\begin{array}{l} \frac{\partial V_{θ}}{\partial t} + V_{r} \frac{\partial V_{θ}}{\partial r} + \frac{V_{θ}}{r} \frac{\partial V_{θ}}{\partial θ} + V_{y} \frac{\partial V_{θ}}{\partial y} + V_{r} \frac{V_{θ}}{r} \\ = - \frac{1}{ρ r} \frac{\partial p}{\partial θ} + ν (\frac{\partial^{2} V_{θ}}{\partial r^{2}} + \frac{1}{r} \frac{\partial V_{θ}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} V_{θ}}{\partial θ^{2}} + \frac{\partial^{2} V_{θ}}{\partial y^{2}} + \frac{2}{r^{2}} \frac{\partial V_{r}}{\partial θ} - \frac{V_{θ}}{r^{2}}), \end{array}

\frac{\partial V_{y}}{\partial t} + V_{r} \frac{\partial V_{y}}{\partial r} + \frac{V_{θ}}{r} \frac{\partial V_{y}}{\partial θ} + V_{y} \frac{\partial V_{y}}{\partial y} = - \frac{1}{ρ} \frac{\partial p}{\partial y} + ν (\frac{\partial^{2} V_{y}}{\partial r^{2}} + \frac{1}{r} \frac{\partial V_{y}}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2} V_{y}}{\partial θ^{2}} + \frac{\partial^{2} V_{y}}{\partial y^{2}}),

\frac{\partial V_{y}}{\partial r} + \frac{V_{r}}{r} + \frac{1}{r} \frac{\partial V_{θ}}{\partial θ} + \frac{\partial V_{y}}{\partial y} = 0 .

Here $v$ is the kinematical coefficient of the liquid viscosity; $ρ$ is the liquid density, $V_{r}$ , $V_{y}$ , $V_{θ}$ is the liquid velocity vector projection on coordinate axis.

The boundary conditions of Eq. (5) are the no-slip conditions for viscous liquid and the ones for the pressure in the absence of leakage at the edges [18, 25]:

6

V_{r} = c o s θ z_{1 m} \frac{d f}{d t}, V_{θ} = - s i n θ z_{1 m} \frac{d f}{d t}, V_{y} = 0, r = R + δ,

V_{r} = c o s θ z_{m} \frac{d f}{d t}, V_{θ} = - s i n θ z_{m} \frac{d f}{d t}, V_{y} = 0, r = R,

\frac{\partial p}{\partial y} = 0, y = \pm \frac{l}{2} .

3. Solutions and discussions

Let us introduce dimensionless variables and the small parameters:

7

\begin{array}{l} ξ = \frac{r - R}{δ}, ζ = \frac{2 y}{l}, θ = θ, τ = ω t, λ = \frac{z_{m}}{δ} ≪ 1, ψ = \frac{δ}{R} ≪ 1, V_{r} = z_{m} ω U_{ξ}, \\ V_{θ} = \frac{z_{m} ω}{ψ} U_{θ}, V_{y} = \frac{z_{m} ω}{ψ} \frac{l}{2 R} U_{ζ}, p = p_{0} + \frac{ρ ν λ ω}{ψ^{2}} P, σ = \frac{l}{2 R} . \end{array}

Here $ψ$ , $λ$ are the small parameters.

As in the considered setting $ψ = o (1)$ , $λ = о (1)$ and $z_{1 m} / z_{m} = O (1)$ , the member at $ψ$ and $λ$ can be omitted in the liquid dynamics Eq. (5) and in the corresponding boundary conditions Eq. (6), written down in variables Eq. (7). As a result, we obtain liquid dynamics problem:

8

\frac{\partial P}{\partial ξ} = 0, \frac{δ^{2} ω}{ν} \frac{\partial U_{θ}}{\partial τ} = - \frac{\partial P}{\partial θ} + \frac{\partial^{2} U_{θ}}{\partial ξ^{2}}, \frac{δ^{2} ω}{ν} \frac{\partial U_{ζ}}{\partial τ} = - \frac{1}{σ^{2}} \frac{\partial P}{\partial ζ} + \frac{\partial^{2} U_{ζ}}{\partial ξ^{2}},

\frac{\partial U_{ξ}}{\partial ξ} + \frac{\partial U_{θ}}{\partial θ} + \frac{\partial U_{ζ}}{\partial ζ} = 0 .

With boundary conditions:

9

U_{ξ} = (\frac{z_{1 m}}{z_{m}}) (\frac{d f_{1}}{d τ}) c o s θ, U_{θ} = 0, U_{ζ} = 0, ξ = 1,

U_{ξ} = (\frac{d f}{d τ}) c o s θ, U_{θ} = 0, U_{ζ} = 0, ξ = 0, \frac{\partial P}{\partial ζ} = 0, ζ = \pm 1 .

The solution of the problem Eq. (8) with boundary conditions Eq. (9) for the established harmonic oscillations regime takes the form of:

10

U_{θ} = \frac{1}{2 ε^{2}} \frac{\partial}{\partial θ} [\frac{\partial P}{\partial τ} (1 + \bar{Ψ} (ξ)) + P \bar{Φ} (ξ)], U_{ζ} = \frac{1}{2 ε^{2} σ^{2}} \frac{\partial}{\partial ζ} [\frac{\partial P}{\partial τ} (1 + \bar{Ψ} (ξ)) + P \bar{Φ} (ξ)],

U_{ξ} = \frac{1}{2 ε^{2}} [\frac{\partial}{\partial τ} (\frac{\partial^{2} P}{\partial θ^{2}} + \frac{1}{σ^{2}} \frac{\partial^{2} P}{\partial ζ^{2}}) ({\bar{Ψ}}_{1} (ξ) - ξ) + (\frac{\partial^{2} P}{\partial θ^{2}} + \frac{1}{σ^{2}} \frac{\partial^{2} P}{\partial ζ^{2}}) {\bar{Φ}}_{1} (ζ)] + \frac{d f}{d τ} c o s θ,

P = 2 ε^{2} α (\frac{d^{2} f}{d τ^{2}} - \frac{z_{1 m}}{z_{m}} \frac{d^{2} f_{1}}{d τ^{2}}) c o s θ + 12 γ (\frac{d f}{d τ} - \frac{z_{1 m}}{z_{m}} \frac{d f_{1}}{d τ}) c o s θ .

Here we introduce the symbols:

γ (ω) = \frac{1}{6} \frac{ε^{3} (s h ε - s i n ε)}{ε^{2} (c h ε + c o s ε) - 2 ε (s h ε + s i n ε) + 2 (c h ε - c o s ε)},

α (ω) = \frac{ε (ε (c h ε + c o s ε) - (s h ε + s i n ε))}{ε^{2} (c h ε + c o s ε) - 2 ε (s h ε + s i n ε) + 2 (c h ε - c o s ε)},

\bar{Ψ} (ξ) = F_{2} (ε ξ) D_{1} - F_{1} (ε ξ) - 2 F_{4} (ε ξ) D_{2}, \bar{Φ} (ξ) = 2 F_{3} (ε ξ) - F_{2} (ε ξ) D_{2} - 2 F_{4} (ε ξ) D_{1},

F_{1} (ε ξ) = c h ε ξ c o s ε ξ, F_{2} (ε ξ) = \frac{1}{2} [c h ε ξ s i n ε ξ + s h ε ξ c o s ε ξ], F_{3} (ε ξ) = \frac{1}{2} s h ε ξ s i n ε ξ,

F_{4} (ε ξ) = \frac{1}{4} [c h ε ξ s i n ε ξ - s h ε ξ c o s ε ξ], D_{1} = \frac{s h ε - s i n ε}{c o s ε + c h ε}, D_{2} = \frac{s i n ε + s h ε}{c o s ε + c h ε},

ε (ω) = \sqrt{\frac{δ^{2} ω}{2 ν}}, {\bar{Ψ}}_{1} (ξ) = \frac{1}{2 ε} [\frac{s h ε ξ s i n ε ξ (s i n ε - s h ε) - c h ε ξ c o s ε ξ (s i n ε + s h ε)}{c h ε + c o s ε}

+ \frac{s i n ε + s h ε}{c h ε + c o s ε} + c h ε ξ s i n ε ξ + s h ε ξ c o s ε ξ],

{\bar{Φ}}_{1} (ξ) = \frac{1}{2 ε} [\frac{s h ε ξ s i n ε ξ (s i n ε + s h ε) + c h ε ξ c o s ε ξ (s i n ε - s h ε)}{c h ε + c o s ε}

- \frac{s i n ε - s h ε}{c h ε + c o s ε} - c h ε ξ s i n ε ξ + s h ε ξ c o s ε ξ] .

In special cases we have ${\bar{Ψ}}_{1} (0) =$ 0, ${\bar{Φ}}_{1} (0) =$ 0, $\bar{Ψ} (1) =$ –1, $\bar{Ψ} (0) =$ –1, $\bar{Φ} (0) =$ 0, $\bar{Φ} (1) =$ 0.

Let us note that in the case of strongly viscous liquid, we can omit inertia members in the Eq. (8). In this case we must take $α =$ 0 and $γ =$ 1 at the pressure expression. As a result, the expressions for vector velocity liquid movement component have the form:

U_{ξ} = \frac{z_{1 m}}{z_{m}} \frac{d f_{1}}{d τ} c o s θ + (\frac{ξ^{2}}{4} - \frac{ξ^{3}}{6} - \frac{1}{12}) (\frac{\partial^{2} P}{\partial θ^{2}} + \frac{1}{σ^{2}} \frac{\partial^{2} P}{\partial ζ^{2}}),

U_{θ} = \frac{1}{2} \frac{\partial P}{\partial θ} (ξ^{2} - ξ), U_{ζ} = \frac{1}{2 σ^{2}} \frac{\partial P}{\partial ζ} (ξ^{2} - ξ) .

By substituting Eq. (10) into Eq. (7), we obtain the expression for dimensional pressure. With taking into account the obtained expression for dimensional pressure, Eq. (4) will take the form of:

11

(m^{*} + M) {\ddot{z}}_{1} + K {\dot{z}}_{1} + n z_{1} = M \ddot{z} + K \dot{z},

where $M = m ν R_{1} (ω δ^{3})^{- 1} 2 ε^{2} α$ , $K = m ν R_{1} δ^{- 3} 12 γ$ , $m = π R^{2} l ρ$ .

We write down Eq. (11) solution for the stationary harmonic oscillations regime in the form of:

12

z_{1} = z_{m} A (ω) s i n (ω t + φ) .

Here $A (ω) = \sqrt{(M^{2} ω^{4} + K^{2} ω^{2}) / {(n - (M + m^{*}) ω^{2})}^{2} + K^{2} ω^{2}}$ is the amplitude frequency characteristic of a hollow cylinder, surrounded by an elastic medium and containing viscous liquid, as well as vibrating cylinder, $φ = a r c t g (K ω / ((M + m^{*}) ω^{2} - n)) - a r c t g (K / M ω)$ .

We introduce the result of the hollow cylinder amplitude frequency characteristics with the following parameters, for example: $R_{1} =$ 5∙10^–2 m, $l =$ 6∙10^–1 m, $h_{0} =$ 4∙10^-3 m, $ρ =$ 1.84∙10³ kg/m³, $v =$ 2.5·10^–4 m²/s, $E =$ 1.96∙10¹¹ Pa, $ρ_{0} =$ 7.87∙10³ kg/m³. In the cases of taking into account surrounding elastic medium we adopt elastic coefficient of Winkler foundation $k =$ 10⁸ N/m³. While in the cases of elastic medium neglecting we adopt $k =$ 0. In the course of calculation, the cases of neglecting inertia members in liquid dynamics equations we take $α =$ 0 and $γ =$ 1 consequently $M = 0$ , $K = 12 m ν R_{1} δ^{- 3} γ$ . The calculation results are presented in Fig. 2.

The solid blue line is the model for $k =$ 10⁸ N/m³with inertia of viscous liquid being taken into account; the dash blue line is the model for $k =$ 0 with inertia of viscous liquid being taken into account; the solid black line is the model for $k =$ 10⁸ N/m³ and without inertia of viscous liquid being taken into account; the dash black line is the model for $k =$ 0 and without inertia of viscous liquid being taken into account.

4. Comparison with the experimental data

Reference [26] presents the data of experimental research of the amplitudes of oscillation rigid cylinder interacting with viscous liquid. This cylinder has an elastic suspension and is inside the elastic cylinder filled with a viscous fluid. In other words, the rigid cylinder forms an inner wall of the annular channel, while an elastic one forms its outer wall. The annular channel formed by the cylinders is set on the foundation vibrating in the vertical plane. By using our approach, we can work out the mathematical model and make the comparison of model calculation and experimental data. To do this, we consider outer elastic cylinder in the form of a rigid one with equivalent mass and an elastic connection with equivalent stiffness coefficient. The equivalent mass and equivalent stiffness coefficient are defined by Eqs. (2), (3). Then the scheme of mechanical system which was investigated in [26] can be presented as in Fig. 3.

Fig. 2The calculation results

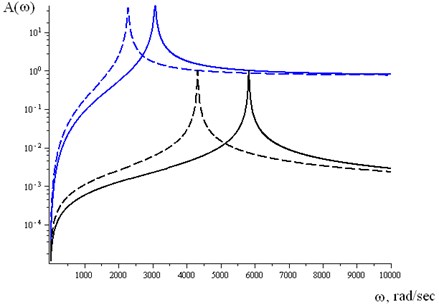
Fig. 3Scheme of mechanical system

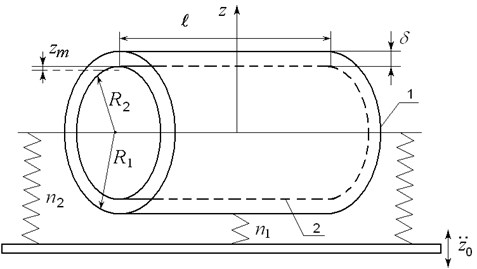
Within this calculation scheme the equations of the annular channel walls movement take the form of:

13

m_{1} ({\ddot{z}}_{0} + {\ddot{z}}_{1}) + n_{1} z_{1} = N, m_{2} ({\ddot{z}}_{0} + {\ddot{z}}_{2}) + n_{2} z_{2} = - N .

Here ${\ddot{z}}_{0}$ is the vibrating foundation acceleration; $z_{1}$ is the outer cylinder movement law; $z_{2}$ is the inner cylinder movement law; $m_{1}$ is equivalent mass of outer cylinder, calculated according to Eq. (3); $m_{2}$ is the inner cylinder mass; $n_{1}$ is the equivalent stiffness coefficient of outer cylinder suspension, calculated according to Eq. (3) where $k =$ 0; $n_{2}$ is the stiffness coefficient of inner cylinder suspension (electronic spring); $N$ is the viscous liquid layer between cylinder reaction defined by Eq. (4).

Taking into consideration foundation acceleration ${\ddot{z}}_{0}$ we write down the expression for pressure in Eq. (7) as $p = p_{0} + ρ ν λ ω ψ^{- 2} P - ρ R_{2} {\ddot{z}}_{0} c o s θ$ . Further, we find expression for $N$ out of the solutions of hydrodynamics Eq. (10) in the form of:

14

N = - m {\ddot{z}}_{0} - M {\ddot{z}}_{1} - K {\dot{z}}_{1} + M {\ddot{z}}_{2} + K {\dot{z}}_{2} .

Here the expressions for $m$ , $M$ , $K$ coincide with Eq. (11).

By substituting Eq. (14) into Eq. (13) and solving them for stationary harmonic oscillations regime under ${\ddot{z}}_{0} = - z_{0 m} ω^{2} s i n ω t$ , we find the inner cylinder movement law:

15

z_{2} = z_{0 m} ω^{2} A_{2} (ω) s i n (ω t + φ_{2}), A_{2} (ω) = \sqrt{\frac{a_{2}^{2} + b_{2}^{2}}{a^{2} + b^{2}}}, φ_{2} = arctg (\frac{a b_{2} - b a_{2}}{a a_{2} + b b_{2}}),

a = (n_{1} - m_{1} ω^{2}) (n_{2} - (m_{2} + M) ω^{2}) - (n_{2} - m_{2} ω^{2}) M ω^{2},

b = K ω (n_{1} + n_{2} - (m_{1} + m_{2}) ω^{2}),

a_{2} = (m_{2} - m) (n_{1} - m_{1} ω^{2}) - M ω^{2} (m_{1} + m_{2}), b_{2} = K ω (m_{2} + m_{1}) .

Here $z_{0 m} ω^{2}$ is the acceleration amplitude of vibrating foundation.

Fig. 4 presents the amplitude oscillations of the inner cylinder under various frequencies of the foundation vibrations; the latter being defined in experimentally in [26] and calculated by Eq. (15) under the foundation vibroacceleration amplitude $z_{0 m} ω^{2} =$ 1 g. In the course of calculating the following parameters we defined according to [26]: $ρ_{0} =$ 8.4·10³ kg/m³, $ρ =$ 2·10³ kg/m³, $ν =$ 3.5·10^-6 m²/s, $E =$ 9.81·10¹⁰ Pа, $l =$ 0.08 m, $δ_{0} / l =$ 6.25·10^-3, $h_{0} / l =$ 1.25·10^-1, $R_{2} / l =$ 3.125·10^-1, $R_{1} / l =$ 31.875·10^-2, $m_{2} =$ 225·10^-3 kg, $n_{2} =$ 1.75·10⁴kg/s².

The comparison of experimental data with calculation ones by the mathematical model worked out by authors presents a good coincidence. This fact proves that the suggested approach to the consideration of the cylinder elastic properties on the basis of one-mass model with equivalent mass and stiffness coefficient is quite legitimate.

Fig. 4The curve 1 is calculation data by Eq. (15); the curve 2 is experimental data from [26]

5. Conclusions

Thus, mathematical model for investigating bending oscillations of a hollow cylinder, surrounded by an elastic medium, filled with viscous liquid and containing vibrating rigid cylinder is suggested. The calculations showed that taking into account only the surrounding elastic medium leads to increasing oscillation resonance frequencies. The resonance frequencies reduce, and amplitude oscillations increase at resonance frequencies are caused by taking into account only liquid movement inertia. Taking into account medium elasticity and viscous incompressible liquid movement inertia simultaneously, leads to further increase resonance frequencies values and the corresponding oscillations amplitudes. Therefore, in the course of modeling real mechanical systems it is necessary to take into consideration viscous incompressible liquid inertia inside hollow cylinder, as well as surrounding elastic medium presence.

References

Gorshkov A. G., Morozov V. I., Ponomarev A. T., Shklyarchuk F. N. Aerogidroelasticity of Designs. Fizmathlit, Moscow, 2000, (in Russian).

Search CrossRef
Avramov K. V., Strel’nikova E. A. Chaotic oscillations of plates interacting on both sides with a fluid flow. International Applied Mechanics, Vol. 50, Issue 3, 2014, p. 303-309.

Publisher
Amabili M. Vibrations of circular plates resting on a sloshing liquid: solution of the fully coupled problem. Journal of Sound and Vibration, Vol. 245, Issue 2, 2001, p. 261-283.

Publisher
Askari E., Jeong K.-H., Amabili M. Hydroelastic vibration of circular plates immersed in a liquid-filled container with free surface. Journal of Sound and Vibration, Vol. 332, Issue 12, 2013, p. 3064-3085.

Publisher
Akcabay D. T., Young Y. L. Hydroelastic response and energy harvesting potential of flexible piezoelectric beams in viscous flow. Physics of Fluids, 24, p. 5-2012.

Publisher
Faria Cassio T., Inman Daniel J. Modeling energy transport in a cantilevered Euler-Bernoulli beam actively vibrating in Newtonian fluid. Mechanical Systems and Signal Processing, Vol. 45, 2014, p. 317-329.

Publisher
Mogilevich L. I., Popov V. S., Popova A. A. Dynamics of interaction of elastic elements of a vibrating machine with the compressed liquid layer lying between them. Journal of Machinery Manufacture and Reliability, Vol. 39, Issue 4, 2010, p. 322-331.

Publisher
Mogilevich L. I., Popov V. S. Investigation of the interaction between a viscous incompressible fluid layer and walls of a channel formed by coaxial vibrating discs. Fluid Dynamics, Vol. 46, Issue 3, 2011, p. 375-388.

Publisher
Ageev R. V., Kuznetsova E. L., Kulikov N. I., Mogilevich L. I., Popov V. S. Mathematical model of movement of a pulsing layer of viscous liquid in the channel with an elastic wall. PNRPU Mechanics Bulletin, Vol. 3, 2014, p. 17-35.

Publisher
Mogilevich L. I. Dynamics of interaction between a squeezed layer of a viscous incompressible fluid and an elastic three-layer plate. Mechanics of Solids, Vol. 43, Issue 5, 2008, p. 785-792.

Publisher
Ageev R. V., Mogilevich L. I., Popov V. S. Vibrations of the walls of a slot channel with a viscous fluid formed by three-layer and solid disks. Journal of Machinery Manufacture and Reliability, Vol. 43, Issue 1, 2014, p. 1-8.

Publisher
Grushenkova E. D., Mogilevich L. I., Kuznetsova E. L., Popov V. S., Rabinsky L. N. Mathematical model of three-layer plate interaction with viscous incompressible liquid layer under foundation vibration. Applied Mathematical Sciences, Vol. 9, Issue 112, 2015, p. 5551-5559.

Publisher
Womersley J. R. Oscillatory motion of a viscous liquid in a thin-walled elastic tube-I: The linear approximation for long waves. Philosophical Magazine, Vol. 46, 1955, p. 199-221.

Publisher
Kondratov D. V., Kondratova J. N., Mogilevich L. I. Oscillating laminar fluid flow in a cylindrical elastic pipe of annular cross-section. Fluid Dynamics, Vol. 44, Issue 4, 2009, p. 528-539.

Publisher
Kondratov D. V., Kondratova J. N., Mogilevich L. I. Studies of the amplitude frequency characteristics of oscillations of the tube elastic walls of a circular profile during pulsed motion of a viscous fluid under the conditions of rigid jamming on the butt-ends. Journal of Machinery Manufacture and Reliability, Vol. 38, Issue 3, 2009, p. 229-234.

Publisher
Kondratov D. V., Kondratova Y. N., Popov V. S., Plaksina I. V. The problem of a hydroelasticity for a tube ring-type a profile with elastic, geometrically irregular outer shell at pressure influence. Izvestiya of Saratov University. New Series. Series: Mathematics. Mechanics. Informatics, Vol. 13, Issue 3, 2013, p. 70-76, (in Russian).

Publisher
Kondratov D. V., Kondratova J. N., Kuznetsova E. L., Mogilevich L. I., Rabinsky L. N. Mathematical model of elastic ribbed shell dynamics interaction with viscous liquid pulsating layer. Applied Mathematical Sciences, Vol. 9, Issue 71, 2015, p. 3525-3531.

Publisher
Mogilevich L. I., Popov V. S. Dynamics of interaction of an elastic cylinder with a layer of viscous incompressible fluid. Mechanics of Solids, Vol. 39, Issue 5, 2004, p. 146-155.

Search CrossRef
Blinkov Yu A., Blinkova Yu A., Mogilevich L. I. Non-linear waves in coaxial cylinder shells containing viscous liquid inside with consideration for energy dispersion. Computational Continuum Mechanics, Vol. 6, Issue 3, 2013, p. 336-345, (in Russian).

Publisher
Blinkov Yu A., Kuznetsova E. L., Mogilevich L. I., Rabinskiy L. N. Nonlinear waves in viscoelastic physically nonlinear cylindrical shell with a viscous incompressible fluid and surrounded by an elastic medium. Journal on Composite Mechanics and Design, Vol. 21, Issue 2, 2015, p. 251-261, (in Russian).

Search CrossRef
Alekseev V. V., Indeitsev D. A., Mochalova Yu A. Resonant oscillations of an elastic membrane on the bottom of a tank containing a heavy liquid. Technical Physics, The Russian Journal of Applied Physics, Vol. 44, Issue 8, 1999, p. 903-907.

Publisher
Kuznetsova E. L., Mogilevich L. I., Popov V. S., Rabinsky L. N. Mathematical model of the plate on elastic foundation interacting with pulsating viscous liquid layer. Applied Mathematical Sciences, Vol. 10, Issue 23, 2016, p. 1101-1109.

Publisher
Mogilevich L. I., Popov V. S., Popova A. A., Christoforova A. V. Mathematical modeling of hydroelastic walls oscillations of the channel on winkler foundation under vibrations. Vibroengineering Procedia, Vol. 8, 2016, p. 294-299.

Search CrossRef
Panovko Y. G., Gubanova I. I. Stability and Oscillations of Elastic Systems. Consultants Bureau Enterprises, New York, 1965.

Search CrossRef
Loitsyanskii L. G. Mechanics of Liquids and Gases. Pergamon Press, Oxford, 1966.

Search CrossRef
Konovalov S. F. Theory of Vibration Resistance Accelerometers. Mashinostroenie, Moscow, 1991, (in Russian).

Search CrossRef

Cited by

About Oscillations in Nonlinear Systems with Elastic Bonds

Valery Ochkov | Inna Vasileva | Yulia Chudova | Anton Tikhonov

(2023)

Proceedings of the 7th International Conference on Industrial Engineering (ICIE 2021)

A. V. Christoforova | V. S. Popov | A. A. Popova

(2022)

Proceedings of the 6th International Conference on Industrial Engineering (ICIE 2020)

D. V. Kondratov | V. S. Popov | A. A. Popova

(2021)

Hydroelastic Response of an End Wall Interacting with a Vibrating Stamp via a Viscous Liquid Layer

V S Popov | A A Popova | A V Christoforova

(2020)

Proceedings of the 4th International Conference on Industrial Engineering

V. S. Popov | L. I. Mogilevich | E. D. Grushenkova

(2019)

Longitudinal Walls Oscillations of an Annular Channel Filled with Pulsating Viscous Fluid

D V Kondratov | V S Popov | A A Popova

(2019)

About this article

Received

15 January 2017

Accepted

14 October 2017

Published

31 December 2017

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2017.18179

Keywords

hydroelasticity

viscous liquid

elastic medium

hollow cylinder

oscillations

amplitude frequency characteristic

one-mass system

Acknowledgements

The reported study was funded by Russian Foundation for Basic Research (RFBR) according to the Research Project No 15-01-01604-a and President of Russian Federation Grant No. MD-6012.2016.8.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 03 20

Rolling and whip phenomenon of hollow rotor slipping on internal stator

A. N. Nikiforov

Research article

2021 06 28

Mathematical modelling of forced oscillations of continuous members of resonance vibratory system

Oleksandr Kachur, Oleksii Lanets, Vitaliy Korendiy, Vasyl Lozynskyy, Oleh Kotsiumbas, Oleksandr Havrylchenko, Nadiia Maherus

Research article

2018 05 22

Hydroelasticity of three elastic coaxial shells interacting with viscous incompressible fluids between them under vibration

Dmitry V. Kondratov, Olga V. Elistratova, Lev I. Mogilevich, Yulia N. Kondratova

Research article

2017 06 30

Mathematical modeling of three-layer beam hydroelastic oscillations

L. I. Mogilevich, V. S. Popov, A. A. Popova, A. V. Christoforova, E. V. Popova

L. I. Mogilevich, V. S. Popov, D. V. Kondratov, and L. N. Rabinskiy, “Bending oscillations of a cylinder, surrounded by an elastic medium and containing a viscous liquid and an oscillator,” Journal of Vibroengineering, Vol. 19, No. 8, pp. 5758–5766, Dec. 2017, https://doi.org/10.21595/jve.2017.18179

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.18179
UR  - https://doi.org/10.21595/jve.2017.18179
TI  - Bending oscillations of a cylinder, surrounded by an elastic medium and containing a viscous liquid and an oscillator
T2  - Journal of Vibroengineering
AU  - Popov, Victor S.
AU  - Mogilevich, Lev I.
AU  - Kondratov, Dmitry V.
AU  - Rabinskiy, Lev N.
PY  - 2017
DA  - 2017/12/31
PB  - JVE International Ltd.
SP  - 5758-5766
IS  - 8
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Popov_2017,
	doi = {10.21595/jve.2017.18179},
	url = {https://doi.org/10.21595/jve.2017.18179},
	year = 2017,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {8},
	pages = {5758--5766},
	author = {Victor S. Popov and Lev I. Mogilevich and Dmitry V. Kondratov and Lev N. Rabinskiy},
	title = {Bending oscillations of a cylinder, surrounded by an elastic medium and containing a viscous liquid and an oscillator},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]V. S. Popov, L. I. Mogilevich, D. V. Kondratov, and L. N. Rabinskiy, “Bending oscillations of a cylinder, surrounded by an elastic medium and containing a viscous liquid and an oscillator,” Journal of Vibroengineering, vol. 19, no. 8, pp. 5758–5766, Dec. 2017, doi: 10.21595/jve.2017.18179.

Copy IEEE

Copied to clipboard!

Popov, Victor S., Lev I. Mogilevich, Dmitry V. Kondratov, and Lev N. Rabinskiy. “Bending Oscillations of a Cylinder, Surrounded by an Elastic Medium and Containing a Viscous Liquid and an Oscillator.” Journal of Vibroengineering 19, no. 8 (December 31, 2017): 5758–66. https://doi.org/10.21595/jve.2017.18179.

Copy Chicago

Copied to clipboard!

Bending oscillations of a cylinder, surrounded by an elastic medium and containing a viscous liquid and an oscillator

Abstract

1. Introduction

2. Mathematical formulation

3. Solutions and discussions

4. Comparison with the experimental data

5. Conclusions

References

Cited by

About this article

Related Articles