In [1] the problem of flat-panel stability connected to elastic base and located in a supersonic gas flow considered. A significant reduction of flutter speed for some values of hardness and compressive force is illustrated there in a case of convergence of the lowest eigenvalues of nonself-adjoint boundary value problem. In this paper we continue to study the influence of elastic ground characteristics to the boundaries position of the stability region, but flat panel is partially connected to the panel. In the case of displaceable supports a study of supercritical panel’s behavior is conducted taking into account the additional longitudinal force.
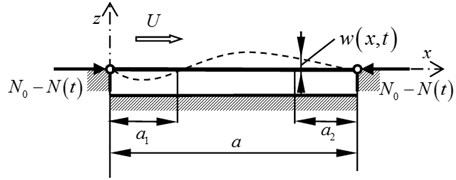
Let’s consider an elastic flat panel (plate), thickness is h, hinged on the sides at x=0 and x=a, elongated in the direction orthogonal to the flow (Fig. 1). This allows us to state that cylindrical plate bending take place and normal deflection in the plate wx,t can be considered as a function of the coordinates x and time t only. In addition, the panel is connected to a system of also extended in the uniform direction elastic reinforcing elements. This direction is perpendicular to the flow direction and these elements are connected to the panel from the section with the coordinate a1 to the section with the coordinate a2 along the axis x. We assume that this site is free-wheeling homogeneous elastic base for the panel. Further we will variate base’s width, so we define linear stiffness properties in the direction of the axis Ox on the section with coordinates a1a2 with full stiffness c as c/a2-a1.
Fig. 1Stiffened panel in the gas stream
Thus, in motion’s equation we include the reactions from the base cwx,t/a2-a1. If a2→a1 i.e. a2-a1→0, the additional support of panel tends to be a support (spring) with stiffness c in the direction of the axis Ox. And the equation will include a term of cwx,tδa1, where δ(x) – delta – Dirac function. The panel is located in a supersonic gas flow with unperturbed velocity U, directed along the axis Ox, and conservative component of loading in the form of a time-constant compressive force N0. The edges of the panel at x=0 and x=a fixed from relative displacements, that cases an additional longitudinal force N(t) in the panel. Pressure p applied to the panel we determine by approximated formula [2]:
where p0 – unperturbed pressure, ρ∞ – density of the gas, U – the incoming flow speed, v – sound speed. Assuming internal and external unperturbed pressure to be equal, we rewrite the equation of dynamic method of studying the stability of a flat form of equilibrium of the panel using dimensionless parameters:
2
where the following parameters are defined:
where D – cylindrical panel stiffness, ρh – the mass of the panel per area unit, εi, εe – coefficients of internal and external friction, ηξ – Heaviside function equal to zero at ξ<0 and equal to one in the other cases, ω0 and N* are the first natural frequency and critical force respectively for the panel hinged along the edges without the elastic foundation in the state of the cylindrical bending.
The study of stability of a flat form of equilibrium of the panel is reduced to the analysis of stability by Lyapunov of the trivial solution of the Eq. (2), i.e. wξ,τ≡0. For this purpose, we apply the method of expansion in their own forms of oscillations [3] with the further application of the Bubnov-Galerkin procedure. We represent the solution of the Eq. (2) wξ,τ as a series of:
where qkτ – generalized coordinates, φkξ=sin(kπξ) forms of natural oscillations of the panel in a state of cylindrical bending, n – the number of retained terms of the series. Substituting Eq. (3) into the Eq. (2) and using the procedure of the Bubnov-Galerkin method, we obtain a system of ordinary differential equations with respect to the generalized coordinates qkτ.
The matrix form of these equations has the form:
4
Elements of matrices A, A12, B, C, D and F are defined in terms of integrals of products forms and their derivatives.
According to Lyapunov theory we hold the linearization of the Eq. (4), and represent the vector of the generalized coordinates in the form of qτ=q0exp(λτ). Then we obtain an algebraic problem of eigenvalues of matrix polynomial in terms of characteristic exponents λ:
where the following notation is defined:
6
Characteristic quantities λ determine the behavior of the system over time in the vicinity of the explored for the stability equilibrium position. The equilibrium will be asymptotically stable if the real parts of the characteristic exponents are negative: ∀Reλ<0. If we change the system parameters and/or load parameters the loss of stability corresponds to a transition of at least one characteristic parameter to the right half-plane. And if this transition occurs through the origin, the type of loss of stability is thus quasi-static in its nature and it is called divergence. If this transition occurs through the imaginary axis with non-zero imaginary part, the type of buckling is oscillatory and it is called flutter. In this case the imaginary part of the characteristic parameter determines the frequency of flutter.
To investigate the stability of the system the criteria of Routh-Hurwitz is applied. Hurwitz matrix is composed of the characteristic polynomial’s coefficients. The vanishing of the determinant of Hurwitz dimension 2n×2n or, that the same, the vanishing of the constant term of the characteristic polynomial b0=0 defines the boundary of divergence. Flutter’s boundary area can be determined from the condition that the principal minor of order 2n-1 equals to zero, i.e. Γ2n-1=0. Thus, the boundary of the stability region is determined by the union of curves defined by equations b0=0 and Γ2n-1=0. The boundaries of the stability region can be identified by direct calculation of the roots of the characteristic Eq. (5) with fixing of crossing point of the complex plane’s λ imaginary axis by them.
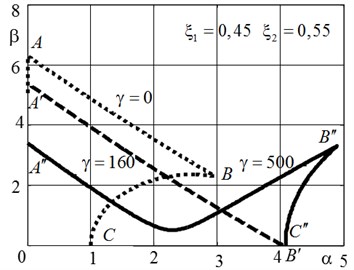
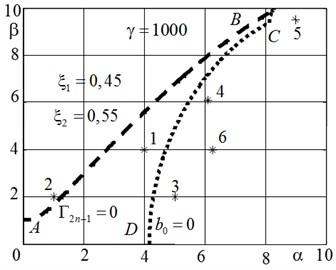
In the study of the stability of the system we take the load parameters α and β as controlling parameters, as well as the rigidity of the elastic foundation γ. The stability region in space α, β, γ is bounded by critical surface. Let’s identify a critical surface sections by the planes γ=const. The results of calculations for determining the position of the boundary of stability with simultaneous action of compressive force α and aerodynamic load β are shown in Fig. 2, 3. Results are given for different values of the elastic foundation stiffness γ. Hereafter, taken ξ1=0,45, and ξ2=0,55 for elastic foundation arrangement, and εe=0,1 and εi=0,01 for the damping coefficients. At Fig.2 the borders of stability regions for three values of the additional elastic support stiffness γ=0, γ=γ1=160 and γ=500 are represented on the plane potential compressive strength α and dissipative component of the aerodynamic load β. γ1 is a stiffness of the base, at which shape buckling is changed under the loading by only the membrane force. If γ=0 (dotted curve), the boundary of the stability region, consisting of border flutter AB and the boundaries of divergence BChas the standard classic look. At γ=γ1 the entire border A'B', bumping into the characteristic value B', is the boundary of a flutter (dashed curve). The boundary of divergence degenerates to a point here. For the case γ=500 the boundary of the flutter (solid line) starting at the point A'' has pronounced minimum in the vicinity of α≈ 2,25, which corresponds to the coincidence of the frequencies, responsible for the flutter. The critical value of the flow rate is determined by the parameters of energy dissipation. After that values β* increases up to the intersection with the boundary of divergence B''C''. For the case when stiffness of the base γ= 1000, the boundary of stability ABCD is shown in Fig. 3. This stiffness value of the base is characterized by the fact that when α= 0 and for previously adopted other parameters of the system critical incident flow speed has the lowest value. For the numbered points on the plane α, β the next step will be the integration of nonlinear equations of perturbed motion. The boundary of the region of stability consists of curves corresponding to the conversion to zero of the main minor of the matrix of Hurwitz Γ2n-1=0 (dashed line ABC – boundary of the flutter) or the free term of the characteristic polynomial b=0 (dotted line CD – border divergence).
Fig. 2The boundaries of the stability region in the parameter plane α, β
Fig. 3The region of stability for the foundation stiffness γ= 1000
Analysis of supercritical behavior of the system was carried out using Eq. (4), taking into account the non-linearity caused by the condition of unbiased panel edges. After integrating Eq. (4) with respect to generalized coordinates with some small initial perturbations by the Eq. (3) a function of a deflection wξ,τ is determined. Some numerical results for the values of stiffness of the elastic support γ= 1000 shown in Fig. 4-8. We studied the behavior of the system at points 1-6, shown in Fig. 3. When loading values α=4 and β=4 (point 1 in Fig. 3 located in the area of sustainability) flat form balance of the panel is asymptotically stable. Displacements tends to zero at t→∞.
Fig. 4The law of motion when buckling on Divergent type
Fig. 5The phase portrait in establishing a stable limit cycle
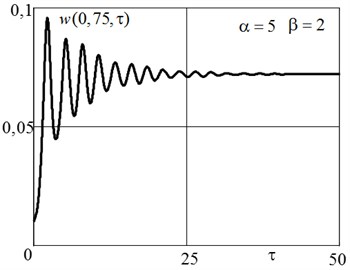
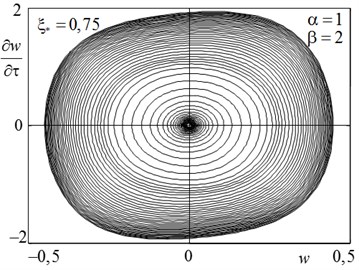
The typical behavior of the system under quasi-static loss of stability are illustrated by Fig. 4 for the point 2 (α= 5, β= 2), which belongs to the region of instability. Here, the system loses stability by divergence type. After the transition damped oscillation process at τ→∞ the panel goes into a curved stable equilibrium position. At α= 1 and β= 2 (point 3 in Fig. 3) phase portrait drawn in Fig. 5 for section ξ=ξ*= 0,75, classic flutter illustrates Andronov-Hopf bifurcation with the establishment of a stable limit cycle.
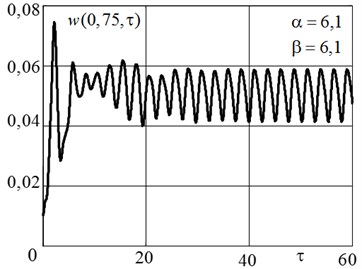
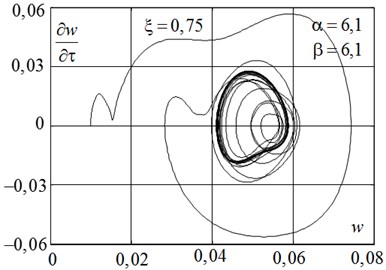
For large values of the loading parameter instability in the region of instability of a plane stability form secondary bifurcations are possible, complex stable and unstable modes of motion, including chaotic. Such phenomena are illustrated on Fig. 6, 8. At point 4 at α= 6,1 and β= 6,1, located in the region of divergence, secondary flutter [4] come true. That can be seen from the law of motion (Fig. 6(a)) and the corresponding phase portrait (Fig. 6(b)).
Here after a “hard” loss of stability (divergence) of the system after a transitional period and a stable limit cycle in the vicinity of a curved equilibrium position of the panel is set.
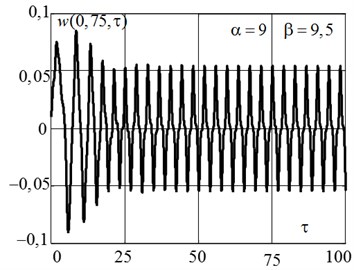
In Fig. 7(a) presents the law of motion at α=9 and β=9,5 at point 5 Fig. 3. The corresponding phase portrait is shown in Fig. 7(b). Here, after a period doubling bifurcation a stable limit cycle with handled symmetrically arranged with respect to the flat form of equilibrium of curved forms of equilibrium is set.
Finally, phase portrait, constructed for the case α=6,25 and β=4 (point 6) in Fig. 8(a), It illustrates the chaotic motion of the panel. The criterion of chaoticity can also serve as the Poincaré section, if these sections form fractal sets in the phase planes. Such a section according to the results of integration of Eq. (4) for a long period of time τ∈0, 100000 for the generalized coordinates q2τ and its derivative with respect to time shown in Fig. 8(b).
Fig. 6The law of motion a) and phase portrait b) in the loss of stability types of secondary flutter
a)
b)
Fig. 7The law of motion a) and phase portrait b) when doubling bifurcation period with the formation of a stable limit cycle
a)
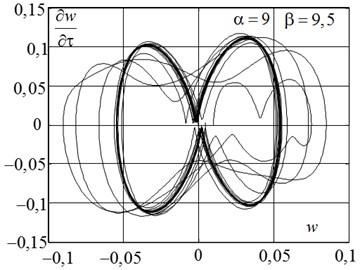
b)
Fig. 8a) The phase portrait of chaotic motions and b) Poincaré section
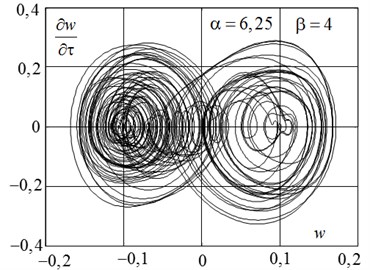
a)
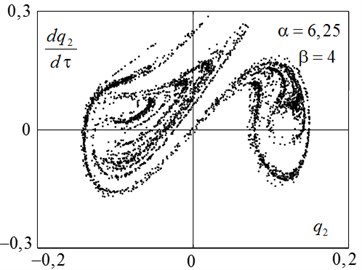
b)
Conclusions
For large values of the loading parameter instability forms of the secondary bifurcations are possible. The criterion of chaoticity can be as the Poincaré section.