Free vibration of thick annular sector plate on Pasternak foundation with general boundary conditions

Liu, Huimin; Liu, Fanming; Bai, Haoran; Yang, Ranbing

doi:10.21595/jve.2016.16717

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2016

Check for updates

Free vibration of thick annular sector plate on Pasternak foundation with general boundary conditions

Huimin Liu¹

Fanming Liu²

Haoran Bai³

Ranbing Yang⁴

^{1, 2}College of Automation, Harbin Engineering University, Harbin, P. R. China

^{3, 4, 1}College of Mechanical and Electrical Engineering, Qingdao Agricultural University, Qingdao, P. R. China

Corresponding Author:

Fanming Liu

Cite the article Download PDF

Downloads 1426

WoS Core Citations 3

CrossRef Citations 4

Abstract

In this paper, the free vibration of the thick annular sector plate on Pasternak foundation with general boundary conditions is presented by using the three-dimensional elasticity theory and the improved Fourier series method. The displacements of the thick annular sector plate are expanded to be the three-dimensional (3-D) Fourier cosine series supplemented with several auxiliary functions to eliminate all the relevant discontinuities of the displacements and their derivatives at the edges with general boundary conditions. This method can be universally applied to any kinds of classical boundaries, elastic boundaries and the combinations of both boundaries without any special change in the solution procedure. The excellent accuracy and reliability of the current solutions are demonstrated by numerical examples and comparison of the present results with those available in the literature. Furthermore, numerous new results for thick annular sector plates on Pasternak foundation with general elastic restrains are presented. In addition, comprehensive studies on the effects of the elastic restraint parameters, geometric parameters and elastic foundation coefficients are also reported.

1. Introduction

Annular sector plates have wide applications in various engineering constructions as one of structure elements, such as aircraft, space vehicles and structures in military industries. However, the annular sector plate structures are often exposed to severe vibration conditions. Therefore, it’s of particular importance to have a good understanding of the vibration characteristics for the thick annular sector plate in the predesign process of the annular sector plate structures. So far, a huge amount of research efforts has been made on the vibration of sector plates by using different methods and plate theories. Ramakris and Kunukkasseril [1] presented a closed-form analytical solution to analyze the free vibration of an annular sector plate with simply supported radial edges. Irie et al. [2] performed the free vibration of ring-shaped polar-orthotropic sector plate with the classical boundary condition by using the Ritz method. Westmann [3] presented an exact and approximate method for free vibration of sector plates with clamped and simply supported boundary conditions. Wang et al. [4] extended the differential quadrature method to analyze the free vibration of thin sector plates with various sector angles and six combinations of classical boundary conditions. Aghdam et al. [5] studied the free vibration analysis of annular sector plates for the clamped support boundary condition by using the extended Kantorovich method. Harik et al. [6] used the finite-strip method to study the free vibration of sector plates with classical boundary conditions. Seok and Tiersten [7] discussed the free vibration of cantilevered annular sector plates by using the variational approximation procedure. Swaminadham et al. [8] compared the natural frequencies of annular sector plates obtained from the finite element method and the experiment. Li et al. [9] used the curve strip Fourier p-element method to study the free vibration of circular and annular sectorial thin plates with classical boundary conditions. The free vibration of annular sector thin plates with classical boundary conditions was studied by Mukhopadhyay [10, 11] and Srinivasan [12] respectively using the semi-analytical method and the integral equation technique. Shi et al. [13] applied the Rayleigh-Ritz method and the improved Fourier series technique to investigate the free vibration of circular, annular and sector thin plate with general boundary conditions. Kim and Dickinson [14] used one-dimensional (1-D) orthogonal polynomials and Liew and Lam [15] adopted two-dimensional (2-D) orthogonal polynomials as the admissible functions to study the free vibration of annular sector plates by the Rayleigh-Ritz method. Ramaiah and Vijayakumar [16] studied the free vibration of annular sector plates with simply supported radial edges by the combination of the Rayleigh-Ritz method and the coordinate transformation. Mizusawa [17] used the spline finite element to analyze the free vibration of annular sector plates with classical boundary condition. Houmat [18] applied the hierarchical finite element method to study the free vibration of annular sector plates. Mirtalaie and Hajabasi [19] performed free vibration analysis of thin functionally graded thin annular sector plates with classical boundary conditions by the differential quadrature method. Liew and Liu [20] studied the free vibration analysis of moderately thick annular sector plates with classical boundary conditions by the differential quadrature method based on the first-order shear deformation theory. Vaidyanathan et al. [21] applied the Rayleigh-Ritz method to study the static analysis of the annular sector mindlin plate. Mizusawa [22] used the finite element method to study the natural frequencies of thick annular sector plates. Leissa et al. [23] considered the effect of stress singularities on the vibration analysis of thick annular sector plates and presented the corner functions to improve the convergence of the numerical solutions. Xiang et al. [24] applied the Ritz method to study the free vibration of thick annular sector plates. Employing the Ritz method and three-dimensional elastic theory, Liew et al. [25] tackled the vibration problem of thick annular sector plates under various classical boundary conditions. Zhou et al. [26] presented the Chebyshev-Ritz method to analyze the three-dimensional free vibration of annular sector plates under various classical boundary conditions.

According to the literature review mentioned above, most of studies on the problem mentioned in the title are usually based on the classical plate theory and the first-order shear deformation plate theory. The results obtained from the three-dimensional elastic theory are very limited. In addition, it is observed that the existing methods or techniques are only suitable for a particular type of classical boundary conditions, i.e., simply-supported supports, clamped boundaries and free edges, which usually leads to constant modifications of the solution procedures and corresponding computation codes to adapt the different boundary cases. Moreover, to the best of our knowledge, there is no work reported on the free vibration behavior of thick annular sector plates on Pasternak foundation with general boundary conditions based on the three-dimensional elastic theory. The only work available in the open literature is that Bhattacharya and Bhowmic [27] used an approximate solution to study the bending analysis of an annular thin sector plate under the free boundary condition and resting on a Winkler-type elastic foundation based on the classical plate theory. Thus, it is desirable to develop a unified and efficient method which is capable of dealing with more complicated boundary conditions involving arbitrary classical boundaries, elastic edge restraints and the combinations of both conditions and structures resting on a Pasternak foundation.

Recently, a modified Fourier series technique proposed by Li [28, 29] is widely used in the vibration analysis of plates and shells with general boundary conditions by the Ritz method, e.g. [30-39]. Based on this, the authors apply the modified Fourier series technique together with the Rayleigh-Ritz method to provide a new three-dimensional exact solution for the free vibration of thick annular sector plates on the Pasternak foundation with general boundary conditions in this paper. The three-dimensional elastic theory is adopted to formulate the theoretical model. The general boundary conditions of the annular sector plate are achieved by the technique of applying the artificial springs on the boundaries. Regardless of the boundary conditions, each displacement of the annular sector plate is expressed as an improved Fourier series which is constructed by a three-dimensional (3-D) Fourier cosine series and several auxiliary functions employed to ensure and accelerate the convergence of the series expansions. All the unknown expanded coefficients are treated equally and independently as the generalized coordinates and obtained directly by using the Rayleigh-Ritz method. The good convergence of the present method is checked and the excellent accuracy and reliability are validated compared with the results presented by other contributors. Some new results of thick annular sector plates with elastic boundary conditions and resting on the elastic foundation are presented, which may serve as benchmark solution for future computational methods. In addition, the effects of the boundary conditions, geometric parameters and elastic foundation coefficients on vibration behaviors of the thick annular sector plate are also presented.

2. Theoretical formulations

2.1. Preliminaries

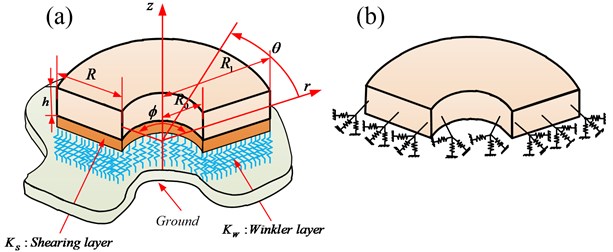
Consider a thick annular sector plate with uniform thickness $h$ , inner radius $R_{0}$ , outer radius $R_{1}$ , width $R$ ( $R = R_{1} - R_{0}$ ) of plate in the radial direction and sector angle $ϕ$ , as shown in Fig. 1. A coordinate system $(r, θ, z)$ is also shown in the Fig. 1, which will be used in the analysis. $u$ , $v$ and $w$ denote the displacement components in $r$ , $θ$ and $z$ directions.

Fig. 1Schematic diagram of the 3-D annular sector plates: a) the geometry and coordinates; b) the boundary restraining springs

According to the small deformation and linear strain-displacement relations, the strain components of thick annular sector plates can be expressed as:

1

ε_{r r} = \frac{\partial u}{\partial r}, ε_{θ θ} = \frac{u}{r} + \frac{1}{r} \frac{\partial v}{\partial θ}, ε_{z z} = \frac{\partial w}{\partial z},

γ_{r θ} = \frac{\partial v}{\partial r} + \frac{1}{r} \frac{\partial u}{\partial θ} - \frac{v}{r}, γ_{r z} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial r}, γ_{θ z} = \frac{\partial v}{\partial z} + \frac{1}{r} \frac{\partial w}{\partial θ} .

Based on the Hooke’s law, the corresponding stress-strain relations of the thick annular sector plates can be written as:

2

σ_{r r} = (Θ + 2 Ξ) ε_{r r} + Θ ε_{θ θ} + Θ ε_{z z},

σ_{θ θ} = Θ ε_{r r} + (Θ + 2 Ξ) ε_{θ θ} + Θ ε_{z z},

σ_{z z} = Θ ε_{r r} + Θ ε_{θ θ} + (Θ + 2 Ξ) ε_{z z},

τ_{r θ} = Ξ γ_{r θ}, τ_{r z} = Ξ γ_{r z}, τ_{θ z} = Ξ γ_{θ z},

where:

3

Θ = \frac{E μ}{(1 + μ) (1 - 2 μ)}, Ξ = \frac{E}{2 (1 + μ)},

in which $E$ and $μ$ are the Young’s modulus and Poisson’s ratio of the thick annular sector plates.

The boundary conditions for a generally supported thick sector plate can be expressed as the following forms based on the force equilibrium relationship on the four edges:

4

r = R_{0} : σ_{r r} + k_{r 0}^{u} u = 0, τ_{r θ} + k_{r 0}^{v} v = 0, τ_{r z} + k_{r 0}^{w} w = 0,

r = R_{1} : σ_{r r} - k_{r 1}^{u} u = 0, τ_{r θ} - k_{r 1}^{v} v = 0, τ_{r z} - k_{r 1}^{w} w = 0,

θ = 0 : τ_{r θ} + k_{θ 0}^{u} u = 0, σ_{θ θ} + k_{θ 0}^{v} v = 0, τ_{θ z} + k_{θ 0}^{w} w = 0,

θ = ϕ : τ_{r θ} - k_{θ 1}^{u} u = 0, σ_{θ θ} - k_{θ 1}^{v} v = 0, τ_{θ z} - k_{θ 1}^{w} w = 0,

in which $k_{i}^{j}$ means the restraining stiffness of the three groups of liner springs along the boundary edges, of which the superscripts and subscripts indicate the type of springs and the location of the corresponding springs, respectively. For example, $k_{r 0}^{u}$ is the stiffness for the liner boundary springs in $r$ direction along the edge $r = R_{0}$ .

2.2. Solution procedure

The strain energy ( $U$ ) of the thick annular sector plate during vibration can be define as:

5

U = \frac{1}{2} \int \int \int_{V} \{ε_{r r} σ_{r r} + ε_{θ θ} σ_{θ θ} + ε_{z z} σ_{z z} + γ_{r θ} τ_{r θ} + γ_{r z} τ_{r z} + γ_{θ z} τ_{θ z}\} r d r d θ d z .

Substituting Eqs. (1)-(2) into Eq. (5), the strain energy expression of the thick annular sector plate can be written as follows:

6

U = \frac{1}{2} \int_{R_{0}}^{R_{1}} \int_{0}^{ϕ} \int_{0}^{h} \{\begin{matrix} (Θ + 2 Ξ) [{(\frac{\partial u}{\partial r})}^{2} + {(\frac{u}{r} + \frac{1}{r} \frac{\partial v}{\partial θ})}^{2} + {(\frac{\partial w}{\partial z})}^{2}] \\ 2 Θ [(\frac{\partial u}{\partial r}) + (\frac{\partial w}{\partial z})] (\frac{u}{r} + \frac{1}{r} \frac{\partial v}{\partial θ}) + 2 Θ (\frac{\partial u}{\partial r}) (\frac{\partial w}{\partial z}) \\ + Ξ [{(\frac{\partial v}{\partial r} + \frac{1}{r} \frac{\partial u}{\partial θ} - \frac{v}{r})}^{2} + {(\frac{\partial u}{\partial z} + \frac{\partial w}{\partial r})}^{2} + {(\frac{\partial v}{\partial z} + \frac{1}{r} \frac{\partial w}{\partial θ})}^{2}] \end{matrix}\} r d r d θ d z .

The corresponding kinetic energy ( $T$ ) function of the thick annular sector plate can be given as:

7

T = \frac{1}{2} \int_{R_{0}}^{R_{1}} \int_{0}^{ϕ} \int_{0}^{h} ρ [{(\frac{\partial u}{\partial t})}^{2} + {(\frac{\partial v}{\partial t})}^{2} + {(\frac{\partial w}{\partial t})}^{2}] r d r d θ d z,

where $ρ$ is the density of the plate and $t$ donates time.

The potential energy stored in the boundary springs is given as:

8

U_{s p} = \frac{1}{2} \int_{0}^{ϕ} \int_{0}^{h} \{R_{0} {[k_{r 0}^{u} u_{}^{2} + k_{r 0}^{v} v_{}^{2} + k_{r 0}^{w} w^{2}]}_{r = R_{0}} + R_{1} {[k_{r 1}^{u} u_{}^{2} + k_{r 1}^{v} v_{}^{2} + k_{r 1}^{w} w^{2}]}_{r = R_{1}}\} d θ d z

+ \frac{1}{2} \int_{R_{0}}^{R_{1}} \int_{0}^{h} \{{[k_{θ 0}^{u} u_{}^{2} + k_{θ 0}^{v} v_{}^{2} + k_{θ 0}^{w} w^{2}]}_{θ = 0} + {[k_{θ 1}^{u} u_{}^{2} + k_{θ 1}^{v} v_{}^{2} + k_{θ 1}^{w} w^{2}]}_{θ = ϕ}\} d r d z .

As mentioned previously, this paper is focused on vibration analysis of the annular sector plate resting on the elastic foundation. As illustrated in Fig. 1, the elastic foundation is achieved by applying the two-parameter elastic foundation (Pasternak) mode with Winkler layer (stiffness $K_{w}$ ) and Shear layer (stiffness $K_{s}$ ). Therefore, the total energy stored by the foundation springs can be given by:

9

U_{F} = \frac{1}{2} \int_{0}^{ϕ} \int_{R_{0}}^{R_{1}} {(K_{w} w^{2} + K_{s} {(\frac{\partial w}{\partial r})}^{2} + K_{s} {(\frac{1}{r} \frac{\partial w}{\partial θ})}^{2})|}_{z = 0} r d r d θ .

To determine the solutions, the Rayleigh-Ritz method is employed. The energy function defined by Lagrangian function is as:

10

L = U + U_{s p} + U_{F} - T .

In the Rayleigh-Ritz method, the solutions can be obtained by minimizing the energy function with respect to the coefficients of the admissible functions. So how to choose the proper admissible functions is the core of present method, for it acts as the most important factor in determining the accuracy and stability of the Rayleigh-Ritz method. It is expected that the displacement functions can be expressed in the form of Fourier series expansions because Fourier functions is of a complete set and exhibits good numerical stability. However, the conventional Fourier series expression generally have a convergence problem along the boundary edges except for a few simple boundary conditions. Thus, if not uniformly convergent, the derivatives of a Fourier series cannot be obtained simply through term-by-term differentiations. To overcome these problems, the displacement function will be here expressed as a more robust form of Fourier series expansion:

11

u (s, θ, z, t) = \{\begin{matrix} \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} \sum_{q = 0}^{\infty} A_{m n q} c o s λ_{R m} s c o s λ_{ϕ n} θ c o s λ_{h q} z \\ + \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} (a_{m n}^{1} ζ_{z}^{1} (z) + a_{m n}^{2} ζ_{z}^{2} (z)) c o s λ_{R m} s c o s λ_{ϕ n} θ \\ + \sum_{m = 0}^{\infty} \sum_{q = 0}^{\infty} (a_{m q}^{3} ζ_{θ}^{1} (θ) + a_{m q}^{4} ζ_{θ}^{2} (θ)) c o s λ_{R m} s c o s λ_{h q} z \\ + \sum_{n = 0}^{\infty} \sum_{q = 0}^{\infty} (a_{n q}^{5} ζ_{s}^{1} (s) + a_{n q}^{6} ζ_{s}^{2} (s)) c o s λ_{ϕ n} θ c o s λ_{h q} z \end{matrix}\} e^{j ω t},

12

v (s, θ, z, t) = \{\begin{matrix} \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} \sum_{q = 0}^{\infty} B_{m n q} c o s λ_{R m} s c o s λ_{ϕ n} θ c o s λ_{h q} z \\ + \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} (b_{m n}^{1} ζ_{z}^{1} (z) + b_{m n}^{2} ζ_{z}^{2} (z)) c o s λ_{R m} s c o s λ_{ϕ n} θ \\ + \sum_{m = 0}^{\infty} \sum_{q = 0}^{\infty} (b_{m q}^{3} ζ_{θ}^{1} (θ) + b_{m q}^{4} ζ_{θ}^{2} (θ)) c o s λ_{R m} s c o s λ_{h q} z \\ + \sum_{n = 0}^{\infty} \sum_{q = 0}^{\infty} (b_{n q}^{5} ζ_{s}^{1} (s) + b_{n q}^{6} ζ_{s}^{2} (s)) c o s λ_{ϕ n} θ c o s λ_{h q} z \end{matrix}\} e^{j ω t},

13

w (s, θ, z, t) = \{\begin{matrix} \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} \sum_{q = 0}^{\infty} C_{m n q} c o s λ_{R m} s c o s λ_{ϕ n} θ c o s λ_{h q} z \\ + \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} (c_{m n}^{1} ζ_{z}^{1} (z) + c_{m n}^{2} ζ_{z}^{2} (z)) c o s λ_{R m} s c o s λ_{ϕ n} θ \\ + \sum_{m = 0}^{\infty} \sum_{q = 0}^{\infty} (c_{m q}^{3} ζ_{θ}^{1} (θ) + c_{m q}^{4} ζ_{θ}^{2} (θ)) c o s λ_{R m} s c o s λ_{h q} z \\ + \sum_{n = 0}^{\infty} \sum_{q = 0}^{\infty} (c_{n q}^{5} ζ_{s}^{1} (r) + c_{n q}^{6} ζ_{s}^{2} (r)) c o s λ_{ϕ n} θ c o s λ_{h q} z \end{matrix}\} e^{j ω t},

where $λ_{R m} = m π / R,$ $λ_{ϕ n} = n π / ϕ,$ $λ_{h q} = q π / h$ and $A_{m n q},$ $B_{m n q},$ $C_{m n q}$ are the Fourier coefficients of three-dimensional Fourier series expansions for the displacements functions, respectively. $a_{m n}^{1}$ , $a_{m n}^{2}$ , $a_{m q}^{3}$ , $a_{m q}^{4}$ , $a_{n q}^{5}$ , $a_{n q}^{6}$ , $b_{m n}^{1}$ , $b_{m n}^{2}$ , $b_{m q}^{3}$ , $b_{m q}^{4}$ , $b_{n q}^{5}$ , $b_{n q}^{6}$ , $c_{m n}^{1}$ , $c_{m n}^{2}$ , $c_{m q}^{3}$ , $c_{m q}^{4}$ , $c_{n q}^{5}$ , $c_{n q}^{6}$ are the supplemented coefficients of the auxiliary functions. As mentioned before, introducing these supplementary terms into the Fourier series is to remove any potential discontinuities of the original displacements and their derivatives throughout the entire plate structure including the boundaries and then to effectively enhance the convergence of the results. According to the three-dimensional elasticity theory, it is required that at least two-order derivatives of the three displacement functions exist and are continuous at any point on the annular sector plates. It can be proven mathematically that the series expansion given in Eqs. (11)-(13) is able to expand and uniformly converge to any function $Ξ (r, θ, z) \in C^{1}$ for $V : ([0, R] \times [0, ϕ] \times [0, h])$ . Also, the series can be easily differentiated, through term-by-term, to obtain uniformly convergent series expansions for up to the second-order derivatives. Since the series expression has to be truncated numerically, the proposed solution should be treated as a solution with arbitrary precision. In actual calculations, we truncate the infinite series expression to $M$ , $N$ , $Q$ to obtain the results with acceptable accuracy.

Substituting Eqs. (6)-(9) and (11)-(13) into Eq. (10) and performing the Rayleigh-Ritz procedure with respect to each unknown coefficient, the equation of motion for plates can be yielded and is given in the matrix form:

14

([\begin{matrix} K_{u u} & K_{u v} & K_{u w} \\ K_{u v}^{T} & K_{v v} & K_{v w} \\ K_{u w}^{T} & K_{v w}^{T} & K_{w w} \end{matrix}] - ω^{2} [\begin{matrix} M_{u u} & 0 & 0 \\ 0 & M_{v v} & 0 \\ 0 & 0 & M_{w w} \end{matrix}]) [\begin{matrix} G_{u} \\ G_{v} \\ G_{w} \end{matrix}] = 0,

where $G$ is the vector of the unknown coefficients. $K$ and $M$ are the generalized stiffness and mass matrices of the thick sector plate, respectively. Obviously, the frequencies (or eigenvalues) of thick annular sector plate can be readily obtained by solving the Eq. (14) and by substituting the corresponding eigenvectors into series representations of displacement components the mode shapes are acquired then.

3. Numerical results and discussion

3.1. Convergence and boundary spring study

Table 1 shows the first six non-dimensional frequency parameters $Ω = ω R_{1}^{2} / {(ρ h / D)}^{\frac{1}{2}} / π^{2}$ ( $D = E h^{3} / 12 (1 - μ^{2})$ ) of the simply supported thick annular sector plate with different truncation numbers $M \times N \times Q$ . The geometry parameters of the annular sector plate are given as: $R_{0} / R_{1} =$ 0.4, $h / R =$ 1/6, $ϕ =$ 90°. From Table 1, it is obvious that the current method has an excellent convergence, and is sufficiently accurate even when only a small number of terms are included in the series expression. When the truncated numbers are changed from 12×12×7 to 18×18×8, the maximum difference of the frequency parameters is within 0.1 % for the worst case, which can be accepted. Furthermore, by comparing the results with those published by Zhou et al. [26], we can find a very good agreement between the two results, although different displacement admissible functions and solution procedures were used in the literature. Moreover, more accurate results may be obtained by more truncated numbers, but the computational cost will increase meanwhile. Therefore, for the sake of both accuracy and computational cost, the truncated number of the displacement expressions will be uniformly selected as $M \times N \times Q =$ 12×12×7 in the following numerical examples.

Table 1Convergence of frequency parameters Ω for annular sector plate with different truncated number M×N×L

$M \times N \times Q$	Mode number
$M \times N \times Q$	1	2	3	4	5	6
9×9×5	5.9442	7.9134	10.947	13.168	14.536	14.571
9×9×6	5.9434	7.9124	10.945	13.165	14.533	14.571
9×9×7	5.9424	7.9110	10.944	13.163	14.532	14.571
9×9×8	5.9418	7.9103	10.945	13.162	14.529	14.570
10×10×7	5.9392	7.9067	10.939	13.157	14.522	14.568
11×11×7	5.9368	7.9038	10.934	13.153	14.514	14.567
12×12×7	5.9324	7.9009	10.931	13.149	14.509	14.566
14×14×7	5.9316	7.8969	10.925	13.144	14.498	14.564
16×16×8	5.9308	7.8961	10.925	13.144	14.498	14.564
18×18×8	5.9305	7.8955	10.924	13.142	14.496	14.563
Ref. [26]	5.9306	7.8931	10.918	13.141	14.490	14.565

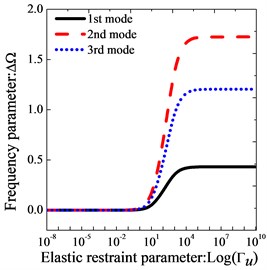
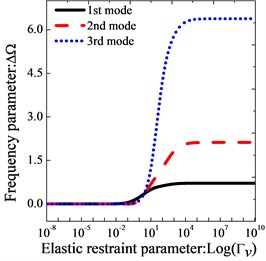
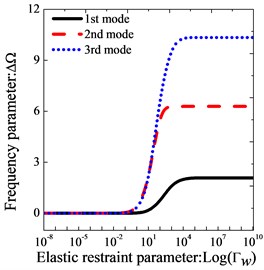
Fig. 2 shows the variation of the lowest three frequency parameters $Δ Ω$ versus the elastic boundary restraint parameters $Γ_{λ}$ for thick annular sector plates. The elastic boundary restraint parameters $Γ_{λ} = L o g_{10} (k_{λ} / D)$ ( $λ = u$ , $v$ and $w$ ) are defined as ratios of corresponding spring stiffness to reference bending stiffness $D$ . In addition, a frequency parameter $Δ Ω$ which is defined as the difference of the non-dimensional frequency parameter $Ω$ to those of the elastic boundary restraint parameters $Γ_{λ (λ = u, v, w)}$ to 10^-8, i.e., $Δ Ω = Ω_{Γ_{λ}} - Ω_{Γ_{λ} = 10^{- 8}}$ is used in the calculation. The geometric parameters of the annular sector plate used are: $R_{0} / R_{1} =$ 0.5, $h / R =$ 0.5, $ϕ =$ 120^o. The thick annular sector plate is free at edges $θ =$ constant and under clamped restraint at $r = R_{0}$ , while at $r = R_{1}$ , the annular sector plate is elastically supported by only one group of spring component with stiffness varying from 10^-8 $D$ to 10¹⁰ $D$ . It is obvious that in certain range the increase of the elastic restraint parameter leads to the increase of the non-dimensional frequency parameter. Thus, the classical boundary condition and general elastic edges can be obtained by setting the stiffness of springs to proper values. Taking edge $r = R_{0}$ for example, the corresponding spring stiffness parameters for four types of classical boundary conditions and three types of elastic boundary conditions which are commonly encountered in engineering practices are given as follows: Clamped boundary condition (C): $k_{r 0}^{u} =$ 10⁸ $D$ , $k_{r 0}^{v} =$ 10⁸ $D$ , $k_{r 0}^{w} =$ 10⁸ $D$ ; Free boundary condition (F): $k_{r 0}^{u} =$ 0, $k_{r 0}^{v} =$ 0, $k_{r 0}^{w} =$ 0; Hard Simply-support boundary condition (S): $k_{r 0}^{u} =$ 10⁸ $D$ , $k_{r 0}^{v} =$ 0, $k_{r 0}^{w} =$ 10⁸ $D$ ; Soft simply-support boundary condition (S¹): $k_{r 0}^{u} =$ 0, $k_{r 0}^{v} =$ 0, $k_{r 0}^{w} =$ 10⁸ $D$ ; E¹ type elastic boundary condition: $k_{r 0}^{u} =$ 10² $D$ , $k_{r 0}^{v} =$ 10² $D$ , $k_{r 0}^{w} =$ 0; E² type elastic boundary condition: $k_{r 0}^{u} =$ 0, $k_{r 0}^{v} =$ 0, $k_{r 0}^{w} =$ 10² $D$ ; E³ type elastic boundary condition: $k_{r 0}^{u} =$ 10² $D$ , $k_{r 0}^{v} =$ 10² $D$ , $k_{r 0}^{w} =$ 10² $D$ . The rationality of defining the boundary conditions in terms of boundary spring parameters will be proved by several examples in the next subsections. For concision, the boundary condition of thick sector plate is expressed by several simple letter strings, such as FCSE¹ identifies the thick annular sector plate with F, C, S and E¹ boundary conditions at boundaries $r = R_{0}$ , $θ =$ 0, $r = R_{1}$ and $θ = ϕ$ .

Fig. 2Variation of the frequency parameters ΔΩ versus the elastic restraint parameters Γλλ=u,v,w for thick sector plate

3.2. Thick annular sector plate with various boundary conditions

In the convergence study, the verification of the present method has been presented in the Table 1. But, it is confined to only one case of the boundary conditions and geometrical parameters. Thus, in this sub-section, the present formulations are applied to study the free vibration of thick sectors with various boundary conditions and geometrical parameters. In Table 2, the comparison of the frequency parameters $Ω$ for annular sector plates with different boundary conditions is presented. The geometry parameters of the annular sector plates are given as: $R_{0} / R_{1} =$ 0.4, $ϕ =$ 90°, $h / R =$ 1/3. Exact 3-D elasticity results provided by Liew et al. [25] and Zhou et al. [26] are involved in the comparison. In addition, the numerical results produced from the ABAQUS based on the FEA method (mesh size:0.02×0.02×0.02) are also shown in Table 2. From the table, we can see that there is a good agreement between the present results and the referential data. The discrepancy is very small and does not exceed 1.79 % for the worst case. The small discrepancy may be attributed to the different solution approaches used. As mentioned before, the mode shapes of the thick annular sector plates can be easily obtained by substituting the corresponding eigenvectors into series representations of displacement components. The comparison of the mode shapes of the thick annular sector plates using the present method and ABAQUS based on FEM is shown in Fig. 3. From the figure, it can be seen that the agreement of the results between these two methods is very good.

Table 2Comparison of frequency parameters Ω for annular sector plates with various boundary conditions (R0/R1= 0.4, θ= 90°, h/R= 1/3)

Boundary conditions	Method	Mode sequence
Boundary conditions	Method	1	2	3	4	5	6
SSSS	Present	2.9972	3.0422	4.5866	4.9811	5.5974	6.7042
	Ref. [25]	2.9973	3.0424	4.5870	4.9818	5.5973	6.7040
	Ref. [26]	2.9973	3.0424	4.5870	4.9818	5.5973	6.7040
SSFF	Present	1.5619	2.3559	2.7834	2.9136	4.0291	4.6820
	Ref. [25]	1.5608	2.3558	2.7829	2.9136	4.0289	4.6820
	Ref. [26]	1.5587	2.3556	2.7827	2.9121	4.0288	4.6812
CCFF	Present	3.8822	4.0323	4.7494	5.2950	6.2421	6.7243
	Ref. [25]	3.8839	4.0336	4.7411	5.2979	6.2429	6.7281
	Ref. [26]	3.8821	4.0318	4.7494	5.2949	6.2415	6.7243
	FE M	3.8801	4.0283	4.7408	5.2939	6.2262	6.7218
CCCC	Present	4.3740	5.6925	7.2910	7.5622	8.5620	9.4663
	Ref. [25]	4.3755	5.6945	7.2911	7.5643	8.5621	9.4678
	Ref. [26]	4.3738	5.5926	7.2904	7.5617	8.5600	9.4663
	FEM	4.3701	5.5884	7.2858	7.5534	8.5488	9.4610

Fig. 3Comparison of the mode shapes for a thick annular sector plate (R0/R1= 0.5, h/R1= 1/3) by using the present method and ABAQUS

a) Annular sector plate with CCFF boundary condition by using present method

b) Annular sector plate with CCFF boundary condition by using ABAQUS

c) Annular sector plate with CCCC boundary condition by using present method

d) Annular sector plate with CCCC boundary condition by using ABAQUS

Table 3Fundamental frequency parameters Ω for annular sector plates with various boundary conditions, thickness ratios and sectors angle (R0/R1= 0.5)

$\frac{h}{R_{1}}$	$ϕ$	Boundary conditions
$\frac{h}{R_{1}}$	$ϕ$	CCCC	CFCS	SFSC	CS¹CS¹	CE¹CE¹	SE²SE²	CE²CE²	E³E³E³E³	E²E³E²E³
1/3	30°	5.6742	3.5112	3.1694	3.5035	3.3599	2.8146	3.4943	1.6672	1.6657
	60°	3.9846	3.4131	2.7038	3.7407	3.3659	2.6999	3.4812	1.3533	1.3494
	120°	3.4976	3.3832	2.5976	3.4512	3.3707	2.6402	3.4170	1.1585	1.1498
	210°	3.4090	3.3773	2.5803	3.4002	3.3738	2.6144	3.3937	1.0988	1.0905
	270°	3.3953	3.3767	2.5789	3.3914	3.3747	2.6068	3.3880	1.0866	1.0789
1/2	30°	3.9274	2.4495	2.3414	2.3376	2.3625	2.3330	2.3336	1.8747	1.8691
	60°	2.8068	2.3956	2.0360	2.4948	2.3642	2.1581	2.4922	1.4852	1.4724
	120°	2.4642	2.3740	1.9731	2.4285	2.3661	2.0537	2.4147	1.2778	1.2523
	210°	2.3942	2.3691	1.9711	2.3867	2.3671	2.0132	2.3846	1.2165	1.2192
	270°	2.3832	2.3685	1.9651	2.3796	2.3674	2.0029	2.3782	1.2041	1.1775
1	30°	2.0323	1.2443	1.3632	1.1701	1.2411	1.7257	1.1697	1.6958	1.6742
	60°	1.4723	1.2531	1.1850	1.2481	1.2396	1.3435	1.2476	1.2706	1.2401
	120°	1.2962	1.2427	1.1601	1.2801	1.2392	1.2068	1.2782	1.1108	1.0501
	210°	1.2556	1.2395	1.1553	1.2512	1.2392	1.1732	1.2508	1.0696	1.0535
	270°	1.2482	1.2393	1.1457	1.2461	1.2391	1.1662	1.2461	1.0617	1.0386

As mentioned previously, most of the existing contributions were restricted to the annular sector plate subjected to a limited set of classical supports. Thus, numerous new results of thick annular sector plates with various boundary conditions and geometry parameters are presented in Table 3. From the Table 3, it is obvious that the frequency parameters of annular sector plates generally decrease with the sector angle $ϕ$ increasing under the classical boundary conditions. However, for the case under the elastic boundary condition, the influence of sector angles on the frequency parameters of annular sector plates becomes more complex. Fig. 4 shows the variation of the first four frequency parameters $Ω$ of the annular sector plate against the sector angle $ϕ$ with different boundary conditions. It can be seen from Fig. 4 that the result under CE²CE²is different from that with other boundary conditions. Under the CE²CE² condition, the frequency parameters increase rapidly as the sector angle $ϕ$ varies from 0° to 30° and then decrease monotonously as the sector angle $ϕ$ keeps increasing. But for the rest of the boundary conditions, the frequency parameters monotonously decrease as the sector angle $ϕ$ increases. Thus, according to the analysis above, the fundamental frequencies of thick annular sector plate are strongly influenced by boundary conditions and geometry parameters.

Fig. 4The variation of frequency parameters Ω of thick annular sector plates (R0/R1= 0.5, h/R1= 0.5) with different sector angles: a) CCCC; b) SSSS; c) CE2CE2; d) E1E2E1E2

The variation of frequency parameters Ω of thick annular sector plates (R0/R1= 0.5, h/R1= 0.5) with different sector angles: a) CCCC; b) SSSS; c) CE2CE2; d) E1E2E1E2

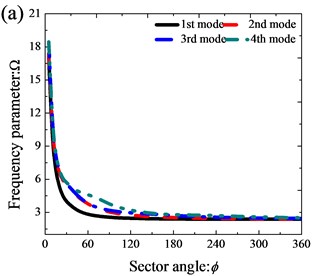
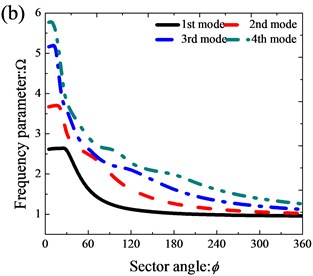
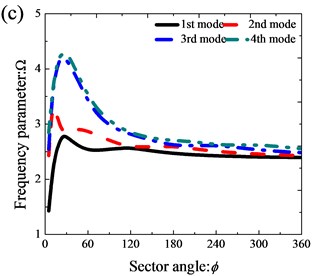
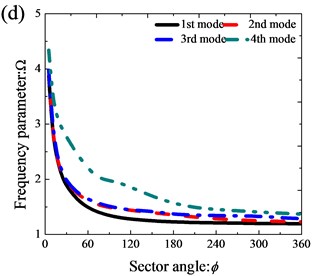
3.3. Thick annular sector plate resting on Pasternak foundations

Firstly, the accessibility of applying the present method to study the vibration analysis of thick annular sector plates resting on elastic foundations need checking. The frequency parameters $Ω$ for the thick annular sector plates with Winkler foundation stiffness are listed in Table 4. The results obtained from ABAQUS based on the FEA method (mesh size:0.02×0.02×0.02) are tabulated in the table for comparison. The geometry parameters of the annular sector plates are: $R_{0} / R_{1} =$ 0.5, $ϕ =$ 90°, $h / R_{1} =$ 0.5. For general purpose, the non-dimensional foundation parameters are used for numerical results as follows: $K_{W} = K_{w} \times R_{1}^{4} / D$ and $K_{S} = K_{s} \times R_{1}^{2} / D$ . In Table 4, the Winkler foundation stiffness $K_{W}$ is set as 10, 100 and 1000. From the table a consistent agreement of present results and referential data is clear. The discrepancy is very small and doesn’t exceed 0.62 % for the worst case. In addition, the table shows that the increasing of Winkler foundation stiffness contributes to the increase of frequencies of the sector plate.

As mentioned before, the results of the thick annular sector plate resting on Winkler/Pasternak foundation are limited in the published literature. Thus, the authors will present some new results of thick sector plates resting on the Winkler/Pasternak foundation with various boundary conditions and foundation coefficients using the present method in the next example. These results can be served as the benchmark solutions for future computational methods in this field. The fundamental frequency parameters $Ω$ for thick annular sector plates with different boundary conditions and elastic foundation coefficients are shown in Table 5.

Table 4Comparison of frequency parameters Ω for annular sector plates with various boundary conditions and thickness ratios (R0/R1= 0.5, θ= 90°, h/R1= 0.5)

$K_{W}$	Mode No.	CCCC			SSSS			CFCF
$K_{W}$	Mode No.	Present	FEM	Error (%)	Present	FEM	Error (%)	Present	FEM	Error (%)
10	1	2.5834	2.5754	0.32	1.2600	1.2601	0.00	2.3956	2.3929	0.12
	2	3.0541	3.0424	0.39	2.0197	2.0191	0.03	2.4442	2.4400	0.19
	3	3.1901	3.1852	0.16	2.2451	2.2421	0.13	2.5511	2.5462	0.20
	4	3.7672	3.7479	0.51	2.6542	2.6532	0.03	2.7350	2.7335	0.07
100	1	2.7241	2.7148	0.34	1.2615	1.2617	0.01	2.5485	2.5462	0.14
	2	3.1412	3.1357	0.18	2.0201	2.0191	0.05	2.5493	2.5479	0.08
	3	3.2157	3.2022	0.43	2.3627	2.3556	0.31	2.5811	2.5770	0.14
	4	3.8435	3.8355	0.21	2.6541	2.6532	0.03	2.8276	2.8138	0.49
1000	1	3.1545	3.1479	0.21	1.2649	1.2650	0.01	2.5516	2.5478	0.15
	2	3.1774	3.1722	0.18	2.0212	2.0207	0.02	2.8683	2.8592	0.32
	3	3.5032	3.5079	0.14	2.6422	2.6378	0.16	2.9306	2.9249	0.20
	4	4.0165	4.0041	0.31	2.6541	2.6532	0.03	3.0724	3.0643	0.26

Table 5Fundamental frequency parameters Ω for annular sector plates with various boundary conditions and elastic foundations coefficients

$\frac{h}{R}$	$K_{W}$	$K_{S}$	Boundary conditions
$\frac{h}{R}$	$K_{W}$	$K_{S}$	CCCC	CFCS	SFSC	CS¹CS¹	CE¹CE¹	SE²SE²	E¹E²E¹E²	E¹E³E¹E³	E²E³E²E³
0.2	10	0	7.5804	7.1688	3.9167	7.4145	7.1302	3.7846	0.3665	0.3691	0.8004
		10	7.8922	7.4653	4.4038	7.7283	7.4141	4.2609	0.5063	0.5064	1.3482
		100	10.179	9.6151	7.3462	10.029	9.4916	7.1434	0.5233	0.5232	2.9215
	100	0	7.6385	7.2306	4.0272	7.4736	7.1925	3.8994	1.0235	1.0243	1.2501
		10	7.9478	7.5245	4.5023	7.7849	7.4737	4.3623	1.0862	1.0862	1.6532
		100	10.222	9.6601	7.4041	10.072	9.5374	7.2032	1.0943	1.0943	3.0736
	1000	0	8.1947	7.8205	4.2929	8.0411	7.7863	4.8962	3.1714	3.1722	3.2791
		10	8.4825	8.0916	5.3853	8.3301	8.0457	5.2705	3.2224	3.2224	3.4445
		100	10.635	10.099	7.9599	10.490	9.9838	7.7746	3.2256	3.2256	4.3054
0.5	10	0	4.5435	4.2766	3.0554	4.4225	4.3022	3.0418	0.4503	0.4708	1.1416
		10	4.9677	4.6832	3.5515	4.8467	4.6866	3.5116	0.6457	0.6476	1.1824
		100	6.6658	6.0255	4.7135	6.6375	6.3919	5.1375	0.7088	0.7088	2.4056
	100	0	4.6366	4.3774	3.1784	4.5164	4.4025	3.1653	1.0305	1.0426	1.4802
		10	5.0457	4.7672	3.6476	4.9243	4.7718	3.6095	1.1492	1.1502	1.5154
		100	6.6985	6.0338	4.7145	6.6703	6.4277	5.1706	1.1883	1.1633	3.0536
	1000	0	5.4060	5.1586	3.3396	5.2773	5.2112	3.9422	2.8205	2.8493	3.1352
		10	5.7036	5.1698	4.3963	5.5505	5.4585	3.9443	3.0376	3.0425	3.1797
		100	6.9935	6.0735	4.7191	6.9663	6.7705	5.4056	3.0715	3.0754	3.9706

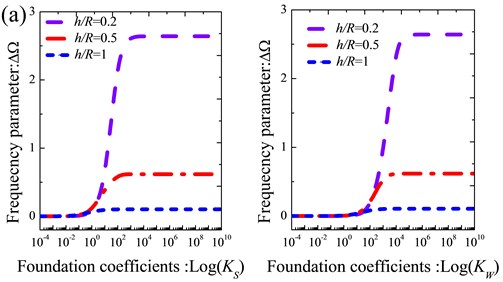
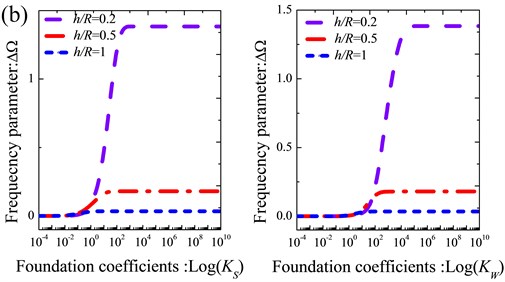
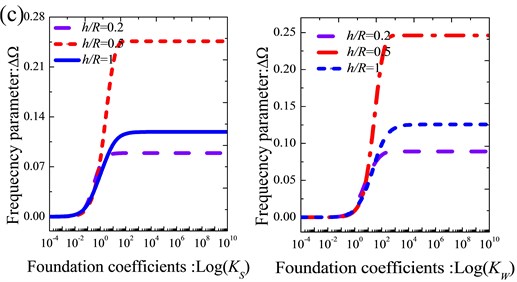
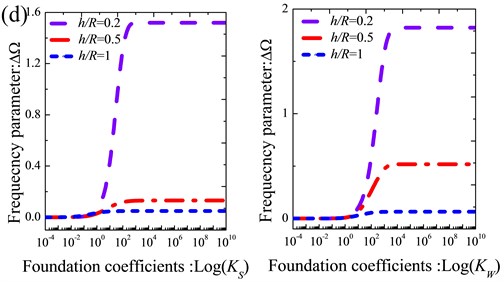
From the tables, it is obvious that the variation of the coefficients has significant effect on frequency parameters of the sector plate. Besides, it also can be found that for the same elastic foundations coefficients, the variation scope of the frequency parameter $Ω$ of the annular sector plate $h / R$ is different with different thickness ratios. In order to further study the influence of foundation coefficients on vibration characteristics of the thick annular sector plate, the variation of the lowest three frequency parameters $Δ Ω$ versus the Winkler foundation stiffness and shearing layer stiffness for thick sector plate is presented in Fig. 5. It can be easily observed that regardless of the boundary condition and geometric parameters of the sector plate, there exists a range of the elastic foundation coefficients in which the frequency parameter $Ω$ increases while the elastic foundation parameter increases and out of which frequency parameter $Ω$ nearly does not change while the elastic foundation parameter keeps increasing. In addition, the influence scope of the frequency parameters of the sector plate expands obviously as the thickness ratio $h / R$ of the annular sector plate decreases. Based on the above analysis, the influence of the elastic foundation coefficients on vibration characteristic is mainly determined by the boundary conditions and geometric parameters.

Fig. 5Variation of the frequency parameters ΔΩ versus the shearing layer stiffness and Winkler foundation coefficients for thick annular sector plate with different boundary conditions: a) CCCC; b) CFCF; c) E1E2E1E2; d) E2E3E2E3

Variation of the frequency parameters ΔΩ versus the shearing layer stiffness and Winkler foundation coefficients for thick annular sector plate with different boundary conditions: a) CCCC; b) CFCF; c) E1E2E1E2; d) E2E3E2E3

4. Conclusions

In this paper, based on the three-dimensional elasticity theory, the free vibration characteristics of thick annular sector plate with general boundary conditions resting on elastic foundation are presented. Regardless of the boundary conditions, each of the annular sector plate displacements is constructed in the form of a standard Fourier cosine series supplemented with several auxiliary functions introduced to eliminate all the possible discontinuities of the original displacement function and its derivatives throughout the entire plate space including the boundaries at the edges and to accelerate the convergence of series representation. The excellent accuracy and reliability of the current solutions are demonstrated by numerical examples and the comparison with the results available in the literature and obtained by using the FEA method. Besides, numerous new results for thick annular sector plates on the Pasternak foundation with elastic boundary conditions are presented. The effects of elastic boundary restraint parameters, boundary conditions, foundation coefficients and sector angles on the frequency values are examined and discussed in detail. The following conclusions can be drawn:

1) For the thick annular sector plate with classical boundary conditions, there is a good agreement between the frequency parameters obtained by the present method and the published results. The results show that the present method is able to converge rapidly and owns high reliability and accuracy.

2) The vibration characteristics of the thick annular sector plates are related to not only the boundary conditions but also their self-properties. In addition, the influence of the elastic foundation coefficients on vibration characteristics is mainly determined by the boundary conditions and geometric parameters.

3) Compared with most of the existing computational methods, the present method can be universally applied to a variety of boundary conditions including all the classical cases, elastic restraints and the combinations of both conditions without the need of change in the solution procedure. Numerous new free vibration results for thick annular sector plates with different geometric parameters and elastic restraints are presented.

References

Ramakrishnan R., Kunukkasseril V. X. Free vibration of annular sector plates. Journal of Sound and Vibration, Vol. 30, Issue 1, 1973, p. 127-129.

Publisher
Irie T., Yamada G., Ito F. Free vibration of polar-orthotropic sector plates. Journal of Sound and Vibration, Vol. 67, Issue 1, 1979, p. 89-100.

Publisher
Westmann R. A Note on Free Vibrations of Triangular and Sector Plates. 2012.

Search CrossRef
Wang X., Wang Y. Free vibration analyses of thin sector plates by the new version of differential quadrature method. Computer Methods in Applied Mechanics and Engineering, Vol. 193, Issue 36, 2004, p. 3957-3971.

Publisher
Aghdam M., Mohammadi M., Erfanian V. Bending analysis of thin annular sector plates using extended Kantorovich method. Thin-Walled Structures, Vol. 45, Issue 12, 2007, p. 983-990.

Publisher
Harik I. E., Molaghasemi H. R. Analytical solution to free vibration of sector plates. Journal of Engineering Mechanics, Vol. 115, Issue 12, 1989, p. 2709-2722.

Publisher
Seok J., Tiersten H. Free vibrations of annular sector cantilever plates. Part 1: out-of-plane motion. Journal of Sound and Vibration, Vol. 271, Issue 3, 2004, p. 757-772.

Publisher
Swaminadham M., Danielski J., Mahrenholtz O. Free vibration analysis of annular sector plates by holographic experiments. Journal of Sound and Vibration, Vol. 95, Issue 3, 1984, p. 333-340.

Publisher
Yongqiang L., Jian L. Free vibration analysis of circular and annular sectorial thin plates using curve strip Fourier p-element. Journal of Sound and Vibration, Vol. 305, Issue 3, 2007, p. 457-466.

Publisher
Mukhopadhyay M. A semi-analytic solution for free vibration of annular sector plates. Journal of Sound and Vibration, Vol. 63, Issue 1, 1979, p. 87-95.

Publisher
Mukhopadhyay M. Free vibration of annular sector plates with edges possessing different degrees of rotational restraint. Journal of Sound and Vibration, Vol. 80, Issue 2, 1982, p. 275-279.

Publisher
Srinivasan R., Thiruvenkatachari V. Free vibration of annular sector plates by an integral equation technique. Journal of Sound and Vibration, Vol. 89, Issue 3, 1983, p. 425-432.

Publisher
Shi X., Shi D., Li W. L., Wang Q. A unified method for free vibration analysis of circular, annular and sector plates with arbitrary boundary conditions. Journal of Vibration and Control, Vol. 22, Issue 2, 2016, p. 442-456.

Publisher
Kim C., Dickinson S. On the free, transverse vibration of annular and circular, thin, sectorial plates subject to certain complicating effects. Journal of Sound and Vibration, Vol. 134, Issue 3, 1989, p. 407-421.

Publisher
Liew K., Lam K. On the use of 2-D orthogonal polynomials in the Rayleigh-Ritz method for flexural vibration of annular sector plates of arbitrary shape. International Journal of Mechanical Sciences, Vol. 35, Issue 2, 1993, p. 129-139.

Publisher
Ramaiah G., Vijayakumar K. Natural frequencies of circumferentially truncated sector plates with simply supported straight edges. Journal of Sound and Vibration, Vol. 34, Issue 1, 1974, p. 53-61.

Publisher
Mizusawa T. Application of the spline element method to analyze vibration of annular sector plates. Journal of Sound and Vibration, Vol. 149, Issue 3, 1991, p. 461-470.

Publisher
Houmat A. A sector Fourier p-element applied to free vibration analysis of sectorial plates. Journal of Sound and Vibration, Vol. 243, Issue 2, 2001, p. 269-282.

Publisher
Mirtalaie S., Hajabasi M. Free vibration analysis of functionally graded thin annular sector plates using the differential quadrature method. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 225, Issue 3, 2011, p. 568-583.

Publisher
Liew K. M., Liu F. L. Differential quadrature method for vibration analysis of shear deformable annular sector plates. Journal of Sound and Vibration, Vol. 230, Issue 2, 2000, p. 335-356.

Publisher
Vaidyanathan S., Busby H., Houser D. A numerical approach to the static analysis of an annular sector Mindlin plate with applications to bevel gear design. Computers and Structures, Vol. 51, Issue 3, 1994, p. 255-266.

Publisher
Mizusawa T., Kito H., Kajita T. Vibration of annular sector Mindlin plates by the spline strip method. Computers and Structures, Vol. 53, Issue 5, 1994, p. 1205-1215.

Publisher
Leissa A., McGee O., Huang C. Vibrations of sectorial plates having corner stress singularities. Journal of Applied Mechanics, Vol. 60, Issue 1, 1993, p. 134-140.

Publisher
Xiang Y., Liew K., Kitipornchai S. Transverse vibration of thick annular sector plates. Journal of Engineering Mechanics, Vol. 119, Issue 8, 1993, p. 1579-1599.

Publisher
Liew K., Ng T., Wang B. Vibration of annular sector plates from three-dimensional analysis. The Journal of the Acoustical Society of America, Vol. 110, Issue 1, 2001, p. 233-242.

Publisher
Zhou D., Lo S., Cheung Y. 3-D vibration analysis of annular sector plates using the Chebyshev-Ritz method. Journal of Sound and Vibration, Vol. 320, Issue 1, 2009, p. 421-437.

Publisher
Bhattacharya A., Bhowmic K. Note on the bending of an annular sector plate resting on an elastic foundation. Journal of Structural Mechanics, Vol. 4, Issue 3, 1976, p. 321-325.

Publisher
Li W. L. Free vibrations of beams with general boundary conditions. Journal of Sound and Vibration, Vol. 237, Issue 4, 2000, p. 709-725.

Publisher
Li W. L. Comparison of Fourier sine and cosine series expansions for beams with arbitrary boundary conditions. Journal of Sound and Vibration, Vol. 255, Issue 1, 2002, p. 185-194.

Publisher
Jin G., Ma X., Shi S., Ye T., Liu Z. A modified Fourier series solution for vibration analysis of truncated conical shells with general boundary conditions. Applied Acoustics, Vol. 85, 2014, p. 82-96.

Publisher
Jin G., Ye T., Chen Y., Su Z., Yan Y. An exact solution for the free vibration analysis of laminated composite cylindrical shells with general elastic boundary conditions. Composite Structures, Vol. 106, 2013, p. 114-127.

Publisher
Jin G., Ye T., Jia X., Gao S. A general Fourier solution for the vibration analysis of composite laminated structure elements of revolution with general elastic restraints. Composite Structures, Vol. 109, 2014, p. 150-168.

Publisher
Jin G., Ye T., Ma X., Chen Y., Su Z., Xie X. A unified approach for the vibration analysis of moderately thick composite laminated cylindrical shells with arbitrary boundary conditions. International Journal of Mechanical Sciences, Vol. 75, 2013, p. 357-376.

Publisher
Shi D., Wang Q., Shi X., Pang F. A series solution for the in-plane vibration analysis of orthotropic rectangular plates with non-uniform elastic boundary constraints and internal line supports. Archive of Applied Mechanics, Vol. 85, Issue 1, 2015, p. 51-73.

Publisher
Jin G., Su Z., Shi S., Ye T., Gao S. Three-dimensional exact solution for the free vibration of arbitrarily thick functionally graded rectangular plates with general boundary conditions. Composite Structures, Vol. 108, 2014, p. 565-577.

Publisher
Jin G., Su Z., Ye T., Jia X. Three-dimensional vibration analysis of isotropic and orthotropic conical shells with elastic boundary restraints. International Journal of Mechanical Sciences, Vol. 89, 2014, p. 207-221.

Publisher
Jin G., Xie X., Liu Z. The Haar wavelet method for free vibration analysis of functionally graded cylindrical shells based on the shear deformation theory. Composite Structures, Vol. 108, 2014, p. 435-448.

Publisher
Wang Q., Shi D., Liang Q. Free vibration analysis of axially loaded laminated composite beams with general boundary conditions by using a modified Fourier-Ritz approach. Journal of Composite Materials, 2015.

Publisher
Wang Q., Shi D., Liang Q., Shi X. A unified solution for vibration analysis of functionally graded circular, annular and sector plates with general boundary conditions. Composites Part B: Engineering, Vol. 88, 2016, p. 264-294.

Publisher

Cited by

Vibration Engineering and Technology of Machinery, Volume II

Ahmad Saood | Mohd. Taha Pervez | Zain Ahmad Khan | Arshad Husain Khan

(2024)

Theoretical modeling and vibration analysis of composite laminated wing-box structures of hydrogen-electric aircraft under hygrothermal environment

Xu-Yuan Song | Wen-Rui Zhao | Jian Zang | Zhen Zhang | Ye-Wei Zhang

(2024)

Review, classification, and extension of classical soil-structure interaction models based on different superstructures and soils

X. Zhao | W.D. Zhu | Y.H. Li | M. Li | X.Y. Li

(2022)

On the Large Amplitude Forced Vibration Analysis of Composite Sectorial Plates

Ahmad Saood | Zain A. Khan | Mohd T. Parvez | Arshad H. Khan

(2021)

About this article

Received

08 December 2015

Accepted

22 April 2016

Published

15 May 2016

SUBJECTS

Modal analysis

DOI

https://doi.org/10.21595/jve.2016.16717

Keywords

thick annular sector plate

three-dimensional elasticity theory

general boundary conditions

Pasternak elastic foundation

free vibration

Acknowledgements

The authors would like to thank the anonymous reviewers for their very valuable comments. The authors also gratefully acknowledge the financial support from the National Natural Science Foundation of China (No. 60834005), National Nature Science Foundation of Shandong Province of China and QingDao Science and Technology Plan Projects under Funds of ZR2013CL021 and 14-2-3-54-nsh respectively.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 11 28

Comparative study for modal analysis of circular plates with various cutouts and end conditions

Vedanth Bhatnagar, Pavan Kishore Mamaduri, Sreenivasulu B

Research article

2017 02 15

Computational approaches to vibration analysis of shells under different boundary conditions – a literature review

Fazl e Ahad, Dongyan Shi, Zarnab Hina

Research article

2016 12 31

A Unified method for vibration analysis of moderately thick annular, circular plates and their sector counterparts subjected to arbitrary boundary conditions

Fazl e Ahad, Dongyan Shi, Anees Ur Rehman, Hafiz M. Waqas

Research article

2016 09 30

An improved Fourier series method for vibration analysis of moderately thick annular and circular sector plates subjected to elastic boundary conditions

Fazl e Ahad, Dongyan Shi, Zarnab Hina, Syed M. Aftab, Hafiz M. Waqas

H. Liu, F. Liu, H. Bai, and R. Yang, “Free vibration of thick annular sector plate on Pasternak foundation with general boundary conditions,” Journal of Vibroengineering, Vol. 18, No. 3, pp. 1692–1706, May 2016, https://doi.org/10.21595/jve.2016.16717

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16717
UR  - https://doi.org/10.21595/jve.2016.16717
TI  - Free vibration of thick annular sector plate on Pasternak foundation with general boundary conditions
T2  - Journal of Vibroengineering
AU  - Liu, Fanming
AU  - Liu, Huimin
AU  - Bai, Haoran
AU  - Yang, Ranbing
PY  - 2016
DA  - 2016/05/15
PB  - JVE International Ltd.
SP  - 1692-1706
IS  - 3
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Liu_2016,
	doi = {10.21595/jve.2016.16717},
	url = {https://doi.org/10.21595/jve.2016.16717},
	year = 2016,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {3},
	pages = {1692--1706},
	author = {Fanming Liu and Huimin Liu and Haoran Bai and Ranbing Yang},
	title = {Free vibration of thick annular sector plate on Pasternak foundation with general boundary conditions},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]F. Liu, H. Liu, H. Bai, and R. Yang, “Free vibration of thick annular sector plate on Pasternak foundation with general boundary conditions,” Journal of Vibroengineering, vol. 18, no. 3, pp. 1692–1706, May 2016, doi: 10.21595/jve.2016.16717.

Copy IEEE

Copied to clipboard!

Liu, Fanming, Huimin Liu, Haoran Bai, and Ranbing Yang. “Free Vibration of Thick Annular Sector Plate on Pasternak Foundation with General Boundary Conditions.” Journal of Vibroengineering 18, no. 3 (May 15, 2016): 1692–1706. https://doi.org/10.21595/jve.2016.16717.

Copy Chicago

Copied to clipboard!

Free vibration of thick annular sector plate on Pasternak foundation with general boundary conditions

Abstract

1. Introduction

2. Theoretical formulations

2.1. Preliminaries

2.2. Solution procedure

3. Numerical results and discussion

3.1. Convergence and boundary spring study

3.2. Thick annular sector plate with various boundary conditions

3.3. Thick annular sector plate resting on Pasternak foundations

4. Conclusions

References

Cited by

About this article

Related Articles