Dynamics rammers with two pairs of shock generators

1.1. Problem setting

The scheme of the considered mechanism is shown on Fig. 1(a), where 1 is the mechanism’s hull in which the bearings contain an axis 2 with a fly wheel 3 and cranks 4 and 5 with radii $r_1$, $r_2$ that have a stationary phase shift $\phi$. The cranks have a joint connection to the piston rods 6 (of length $l_i$); percussion pistons 7 and 8 are, in turn, connected to them with a joint. Under the percussion pistons we have anvils 9, 10 with heights $h_1$, $h_2$ respectively. The hull 1 has a joint connection to the racks 11 that are rigidly connected to the anvil block 12. The rotation of the axis in the proposed scheme is transformed with a crank mechanism into a back-and-forth motion with respect to the anvil block. The percussion pistons may alternate their blows to the corresponding anvils, and the vibro-impact created here is transmitted through the anvil block to the material being compacted.

Fig. 1The scheme of the considered mechanism

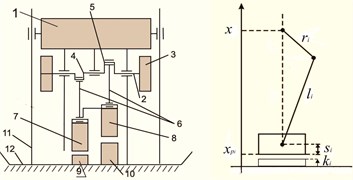
We denote by $x$ the coordinate of the hull’s center of mass $M$, by $x_{pi}$ ($i=$ 1, 2), coordinates of the percussion piston masses mi, and compose expressions for kinetic $V$ and potential $\mathrm{\Pi }$ energies presenting the Lagrange function as:

also, using obvious relations $r_1\ll l$, $r_2\ll l$, and assuming $l_i\approx l$, $i=\mathrm{}$1, 2, we represent the mechanism’s motion equations as Eq. (1), (2):

where we have introduced the following notation: $\tau =\omega t$, $x=(x_{star}-s_2-l)l^{-1}$, $\mu =r_1{l}^{-1}$, $\gamma =r_2{l}^{-1}\text{,}$$p=g({\omega }^{2}l{)}^{-1}\text{,}$$\epsilon =(s_1-s_2)l^{-1}\text{,}$${\lambda }_i=m_i(M+{\sum }_{i=1}^2{m}_i{)}^{-1}\mathrm{}(i=1,\mathrm{}2)\text{,}$ while ${\left.dx/d\tau \right|}_{+}={\dot{x}}^{+}$, ${\left.dx/d\tau \right|}_{-}={\dot{x}}^{-}$ are velocities immediately after and before the impact.

1.2. Solution method

Phase space for system $Ф$($x\ge f\left(\tau \right)$, $\dot{x}<+\mathrm{\infty }$) in coordinates $x$, $\dot{x}$, $\tau$ is reduced with respect to $x$. The surface $S$($x=f\left(\tau \right)$) is a cylindrical surface formed by an intersection of two surfaces $x=f_1\left(\tau \right)$, $x=f_2\left(\tau \right)$. All phase trajectories are located either on the surface $S$ or above it. If $x>f\left(\tau \right)$ it corresponds to free motion of the mechanism; if $x=f\left(\tau \right)$, it corresponds to an impact interaction of one of the pistons with the stop (anvil block). Phase trajectories are shown on Fig. 2 in a qualitative form. In case of an impact motion for $R\ne 0$ the depicting point moves in the phase space $\mathrm{\Phi }$ as follows: moving in the region $G(x>f(\tau \left)\right)$, it reaches the surface $S$ at some point $M_0^{\mathrm{\text{'}}}({\tau }_0,x_0=f({\tau }_0),{\dot{x}}_0)$ and then instantaneously moves along the surface $S$ up to a certain point $M_0\left({\tau }_0,x_0=f\left({\tau }_0\right),{\dot{x}}_0^{+}=-R{\dot{x}}_0+(1+R){\left.\frac{df}{d\mathrm{\tau }}\right|}_{\tau ={\tau }_0}\right)$ and then, having left $S$, moves according Eq. (1) in $G$ until it reaches the surface $S$ again at some point $M_1^{\mathrm{\text{'}}}({\tau }_1,x_1=f({\tau }_1),{\dot{x}}_1)$. Thus, the depicting point will reach surface $S$ every time.

The class of trajectories described above corresponds to a lengthy stop of one of the pistons or to successive “trampling” of the pistons. We must note that the form of the surface $S$ shown on Fig. 2 is preserved only if surfaces $S_1$ and $S_2$ intersect.

Fig. 2The surface S

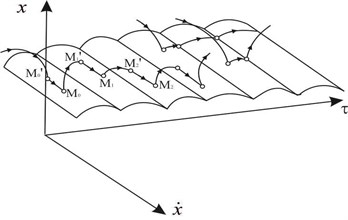
However, it is clear that impact motions of the mechanism are possible if only one of the pistons interacts with the anvil. Then the surface $S$ will be a smooth cylindrical surface with equation either $x=f_1\left(\tau \right)$ or $x=f_2\left(\tau \right)$. Using equations $x=f_1\left(\tau \right)$, $x=f_2\left(\tau \right)$ we can get a relation on the mechanism parameters:

Thus, the description of the phase space structure and the behavior of phase trajectories in it imply that as a section plane [7] we can take the surface $S$ and study the dynamics with the method of point maps [7, 8]. In this case, it means mappings of the section plane $S$ onto itself.

1.3. Constructing a point map

Let:

be three consecutive points that belong to the surface $S$; then a transformation $T=T_2\mathrm{}{T}_1$ of the points $M_0\stackrel{T_1}{\to }{M}_1\stackrel{T_2}{\to }{M}_2$ can be written as:

1.4. Existence and stability conditions for fixed points at a point map t corresponding to periodic two-impact motion modes

Equations for finding the coordinates of fixed points on a point map $T$ corresponding to two-impact periodic motions (with consecutive impacts by each percussion piston) results by adding periodicity conditions [8] to Eq. (3-5):

Resolving system Eq. (4-6) with respect to $\dot{x}$, ${\dot{x}}_1$, ${\tau }_0$, ${\tau }_1$, we get:

1.5. Results of numerical experiments

Our study of the mechanism’s complex dynamics has been augmented by numerical experiments that employ a software suite developed in the Borland C++ Builder 6 IDE. We denote by $D(m_1,m_2)$the existence and stability region for periodic motions in the space of parameters, where $m_1$ and $m_2$ denote the number of impacts by the first and second percussion piston against the anvil block respectively. Fig. 3 shows the bifurcation diagram built for of parameters $(\mu =\text{0.12}$, $\epsilon =\text{0.018}$, $\gamma =\text{3}$, $\phi =\text{3.14}$, ${\lambda }_1=\text{0.2}$, ${\lambda }_2=\text{0.3}$, $k_1=\text{0}$, $k_2=\text{0})$. The horizontal axis on the diagram shows the values of the frequency parameter $p$; the vertical axis, values of post-impact velocities ${\dot{x}}_i^{+}\in f\left(\tau \right)\text{.}$ Fig. 3(a) corresponds to the diagram with impacts by first piston ${\dot{x}}_i^{+}\in f_1\left(\tau \right)$; Fig. 3(b), to the diagram with impacts by the second piston ${\dot{x}}_i^{+}\in f_2\left(\tau \right)$.

Fig. 3Bifurcation diagrams

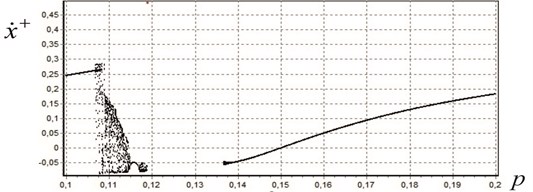
a) For the first piston

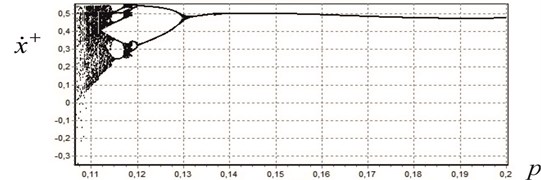
b) For the second piston

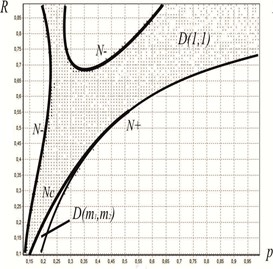
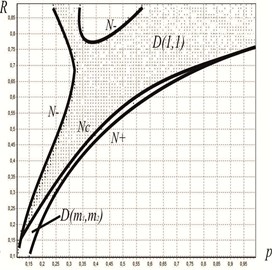
Fig. 4Areas of the existence and stability of periodic motions with alternating strokes of the pistons: a) k1=0, k2=0, b) k1=0.2, k2=0.3

a)

b)

The pictures show that for frequencies $\text{0.135}\le p\le \text{0.2}$ there exists a periodic motion with $m_1=\text{1}$, $m_2=\text{1}$; for frequencies $\text{0.13}\le p\le \text{0.135}$, periodic motion modes with $m_1=\mathrm{}$1, $m_2=\mathrm{}$0 (there occur periodic strikes by only one piston); for frequencies $\text{0.12}\le p\le \text{0.13}$ we observe periodic motion modes with two strikes of only one piston ($m_1=$ 2, $m_2=\text{0}$); with four ($\text{0.118}\le p\le \text{0.12}$$m_1=\mathrm{}$4, $m_2=0$) and, finally, in the interval $\text{0.1}\le p\le \text{0.118}$ we see a chaotic motion mode. Values of frequencies $p=\text{0.12}$ and $p=\text{0.13}$ are bifurcational since as their values increase, we see that the number of strikes by the first piston doubles (the period doubling process), which is known to lead to chaotic motion [9]. With our software suite, we performed numerous computations, in particular, constructed existence and stability regions for periodic motion modes as a function of the relative value of the supports for percussion pistons. For instance, Fig. 4(a) shows, in the plane $\left(p,R\right)$, the region $D\left(\mathrm{1,1}\right)$ (dashed region) for the following set of parameters (without supports):

and the bifurcation boundary $N_c$ [8]. In the region $D(m_1,m_2)$, where $m_1$ and $m_2$ are not simultaneously equal to 1, there exist motions with several (more than two) strikes by each of the pistons. Fig. 4(b) shows the existence and stability region for the periodic motion ($m_1=\mathrm{}$1, $m_2=$ 1) for the values of parameters shown above with relative support height $k_1=\mathrm{}$0.2, $k_2=$ 0.3. This figure indicates that the use of supports for percussion pistons lets us extend the range of parameters in order to tune the mechanism for a certain stable motion mode.