The dynamics of eccentric vibration mechanism (Part 1)

1. Introduction

Recently, alongside with shock-vibration mechanisms with unbalance vibration exciters, eccentric shock-vibration mechanisms (ESVM) with a crank-sliding bar vibration exciter (CSVE) [1, 2] have come to be widely used in civil engineering. This innovative design was based on the principle of “the inverted vibrator”, with its working unit, unbalanced mass, hinged on an eccentric shaft and balanced in rotation by the unbalanced mass. The loading pulse transmitted onto the surface (ground, piles etc.) is produced both due to a spreader with a shoulder of the eccentric shaft and due to the kinetic energy of the falling of the working unit. The effectiveness of compacting and immersing machines not only depends on the quantity of the energy transmitted to the medium being processed, but, to the larger extent, on the character of transmitting this energy – the pulse “form” which should be varied by rearranging certain dynamic factors of a single loading pulse. It is evident that a dense and, at the same time, strong structure of the ground can be achieved only when specific pressure on the surface of the contact of the working unit and the ground in the process of compaction is increased by degrees, its lower limit being determined by the physical properties of the ground in its initial state (before compaction), and the upper one by the ultimate strength of the ground or by technological conditions. Thus, parameters of such machines and mechanisms must be defined from the conditions close to quasi-plastic interaction. Besides, the pulse rate in each single cycle must be such that it precludes possible development of elastic aftereffects of the processed medium in the intervals between the pulses. Such multi-pulse loading mode can be realized using multi-striker ESVM with CSVE designed to easily regulate working modes by changing the geometry of cinematic connections and to solve the problem of compaction of soils in strained conditions of industrial and civil engineering processes. The variety of problems that require the study of dynamic models with discontinuous or piecewise-continuous non-linearities is enormous. They include dry friction systems, shock-vibration and relay systems, variable-structure control systems, numerous mechanic, electric- and radio-technical systems with non-smooth characteristics of certain elements, etc. The investigators’ interest for such substantially nonlinear systems remains alive. Thus, nonlinear dynamic problems of vibration systems with impact interaction of the elements are currently being analyzed by scientific teams headed by B. I. Van de Vrande, D. N. Van Campen, P. I. Leine, G. W. Luo, V. K. Astashov, V. I. Babitsky, М. I. Feygin et al. [3-18]. These works analyzed the complex dynamics of vibration systems with impact interactions of various nature. Periodical motion modes in non-self-supporting systems with finite (mostly with one) and infinite (quasi-plastic) number of impacts during one period of the periodic motion have been studied. Where possible, the mathematical apparatus of the point mapping method [17-29] was used in the studies. The systems and mechanisms used as vibro-impact rams for various media (soils, concrete, loose materials etc.) as well as for driving in or extracting piles, were designed in the form of unbalance mechanisms. The designs of such mechanisms, especially when being used as vibro-impact rams, often could not cope with their tasks for various reasons. One of such reasons is their being unsuited for working in conditions of limited space, as well as being highly power-consuming.

The innovative design of a shock-vibration mechanism with a random (finite) number of sliding bar-strikers [2] can provide ramming of, for instance, soil (concrete) with higher quality and lower power consumption in spatially limited conditions. At the same time, the introduction of additional impact couples makes the behavior of the mechanism more complicated. That is why the dynamic analysis of such systems and the study of their properties, accounting for the impact interaction with the processed media, is an important issue of both scientific and practical interest. However, the scientific literature available gives no account of certain important aspects of the behavior of such systems. In the first place, it concerns bifurcations related to the expansion of the phase trajectory of a periodical solution stitched up of separate portions beyond the sub-regions of its definition and having no counterparts in analytical systems.

In this connection, the work presents a mathematical model of multi-striker ESVM with CSVE with and without account for the motion of the processed medium, describes the structure of the phase space of model and, based on this and using the point mapping method, determines analytical relations for finding in the parameter space the boundaries of the regions of existence and stability of periodical motion modes. Additionally, relations for the system parameters are given that make it possible to do preliminary tuning of the mechanism onto to main working mode. Using numerical computations with the help of a software complex developed in the Borland C++ Builder 6, bifurcation diagrams were obtained which make it possible to monitor the main changes of the motion modes of the mechanisms.

2. Problem setting

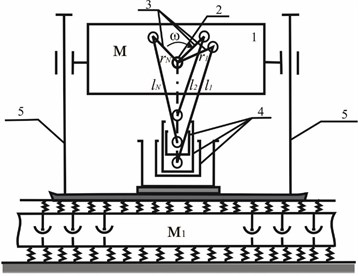
The impact-vibration mechanism considered in the paper (Fig. 1) consists of the frame 1 encasing the eccentric shaft 2 with flywheels at its ends. On the shaft, there are eccentric mechanisms 3, each consisting of two eccentrics nested into each other with a possibility to change the position of the washers, which makes it possible to regulate the value of eccentricity $r_i$ and phase shift ${\phi }_i$ between them ($i=$ 1, 2, ..., $N$). Slides-strikers (SS) 4 are hinged at the free ends of the connecting rods. The eccentric mechanisms in combination with the connecting rods and SS convert the rotary motion of the of the shaft with the constant cyclic rate of rotation of the flywheel into reciprocating motion of the frame relative to stands 5. Each SS strikes its own anvil.

The processed medium (soil, pile, etc.) is represented as an elastically fastened mass $M_1$ with elasticity coefficient $C$. Energy losses in the slide-bars of the frame and the medium is accounted for in the form of viscous friction with equivalent damping coefficients $b$ and $b_1$, respectively.

As the eccentrics can be phase-shifted by angles ${\phi }_i$ relative to each other and have, generally speaking, different lengths, the body oscillates relative the mechanism with the largest sum of projections of the geometrical dimensions onto the vertical axis at the moment. The impact on the anvil of one or several SS’s takes place either during the change of SS’s interacting with the anvil, or after the breakage of the body together with the eccentric mechanisms.

Fig. 1The impact-vibration mechanism

Neglecting the masses of SS’s, connecting rods and cranks, the equation of free (without impact) motion of the system for $y_{pi}>y_c$ can be written in the following form:

where $y$ – coordinate of the mass centre of the body counted off from the equilibrium position of mass $M_1$ for a non-deformed spring $C$, $y_c$ is deviation value of mass $M_1$ from the same initial point, $y_{pi}$ are values characterizing deviation of bases of the $i$th SS, $g$ is free-fall acceleration.

When one of the SS contacts the medium $y_{pi}=y_c$ there takes place either a momentary impact interaction, such that if ${\dot{y}}_{pi}^{-}$, ${\dot{y}}_c^{-}$ and ${\dot{y}}_{pi}^{+}$, ${\dot{y}}_c^{+}$ are velocities of the $i$th SS and the medium immediately before and after the impact interaction, respectively, then:

Or simultaneous ($R=$ 0) motion of the shock-vibration mechanism with the medium described by the following equation:

In Eqs. (2) the following definitions are used: 0$\le R\le$1 is impact velocity recovery coefficient, ${\mu }_0=M/M_1$.

The position of the eccentricities of length will be measured by angles ${\theta }_i=\omega t-{\phi }_i$, counted off the vertical axis. Then it follows that:

where $s_i$ is distance from the fixture point of the $i$th connecting rod to the base of the $i$th SS, $l_i$ is length of the $i$th connecting rod.

When changing in system (1-4) to dimensionless time $\tau =\omega t$, coordinates $x=(y-s_2-l)/l$, $x_1=y_c/l$ of the body and the medium, parameters:

As well as introducing function $f_i\left(\tau \right)={\epsilon }_i-\mu {\gamma }_i\mathrm{c}\mathrm{o}\mathrm{s}(\tau -{\phi }_i)$, for $r_i\le \le l$ the following equations describing impact-oscillatory motions of the mechanism, accounting for the mobility of the processed medium, are obtained:

$\tau$-periodical function $F\left(\tau \right)$ on Eqs. (6) describing simultaneous motion of the striking mechanism with the medium after the impact of the $i$th SS has the following form:

3. Solution method

Assuming $x_1=$ 0, $M_1=\infty$, $h=$ 0 in Eqs. (5-7), the equations of motion with momentary stops [3] of one or several SS’s can be rewritten as:

The phase space of system Eq. (8) in coordinates $x$, $\dot{x}$, $\tau$ is truncated along $x$, and, besides, $x\ge f\left(\tau \right)$, $\dot{x}<+\infty$ (Fig. 2).

Fig. 2The phase space

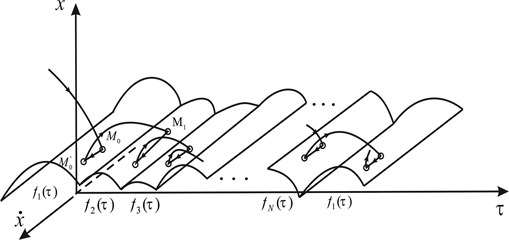
All the phase trajectories are situated either along the surface $x=f\left(\tau \right)$ ore above it, which represents (generally speaking) $N$ of intersecting cylindrical surfaces $x=f_i\left(\tau \right)$ ($i=$ 1, 2, ..., $N$). The case of $x=f\left(\tau \right)$ corresponds to free motion of the falling mechanism, and $x=f\left(\tau \right)$ corresponds to impact interaction of one of the SS’s with the stopper.

In the case of impact interactions of SS with the stopper for $R\ne$ 0, the representing point in the phase space moves as follows: from region ${\mathrm{\Phi }}_1(x>f(\tau \left)\right)$, the representing point gets on surface $\mathrm{\Pi }(x=f(\tau \left)\right)$ into a point ${{\rm M}}_0({\tau }_0,x_0=f({\tau }_0),{\dot{x}}_0)$ (see Fig. 2), and then, moving along surface $\mathrm{\Pi }$ into point ${{\rm M}}_0^1({\tau }_0,x_0=f({\tau }_0)$, ${\dot{x}}_0^{+}=-R{\dot{x}}_0+(1+R)df\left({\tau }_0\right)/d\tau$), leaves it and gets into subspace ${\mathrm{\Phi }}_1$, where it stays until it gets once again onto surface $\mathrm{\Pi }$ into a point ${{\rm M}}_1({\tau }_1>{\tau }_0,x_1=f({\tau }_1),{\dot{x}}_1)$, etc. If at a time $\tau ={\tau }_i$, when the representing point gets onto surface $\mathrm{\Pi }$ into point ${{\rm M}}_i({\tau }_i,x_i=f({\tau }_i),{\dot{x}}_i)$, the value before the impact velocity is equal to the velocity of change $f\left(\tau \right)$ at that moment, or a limiting case of the value of the velocity recovery coefficient is considered for the impact $R=$ 0, then the representing point displaces from ${{\rm M}}_i$ to point ${{\rm M}}_i^1\left({\tau }_i,x_i,{\dot{x}}_i^{+}=df\left({\tau }_i\right)/d\tau \right)$ and then will slide along surface $\mathrm{\Pi }$ until, at time ${\tau }_s$, it reaches boundary $\mu {\gamma }_i\mathrm{c}\mathrm{o}\mathrm{s}({\tau }_s-{\phi }_i)+p=$ 0 of the sliding potion plate. These time intervals ${\mathrm{\Delta }}_{si}={\tau }_s-{\tau }_i$ correspond to prolonged contacts of SS with the stopper.

In what follows, the main attention will be paid to periodical motion modes with successive impacts of each SS during period $Г$. It is evident that such a mode is only possible under the condition of paired intersection of two successive surfaces $f_k\left(\tau \right)$, $f_{k+1}\left(\tau \right)$. For this to be possible, the following relations for the system parameters must hold:

If for any pair $f_l\left(\tau \right)$, $f_{l+1}\left(\tau \right)$ this inequality does not hold (no intersection of the surfaces) then, in the technological process of the motion of the mechanism, the mode with the stroke of the $l$th or the $(l+1)$th SS is skipped. To this end, conditions Eq. (9) are of paramount importance when adjusting a specific mechanism to the mode with alternating strokes of each of the SS’sN.

4. Constructing a point map

It follows from the description of the structure of phase space $\text{Φ}$ in system Eq. (8) that the dynamics of the mathematical model considered can be investigated by studying the properties of the point transform [18-19, 24-29] $T$ of surface $\mathrm{\Pi }$ into itself.

Let us introduce into the analysis the simplest point transforms ${{\rm T}}_{k+1}$ transforming surface points $x=f_{k+1}\left(\tau \right)$ into surface points $x=f_{k+2}\left(\tau \right)$, which, using (8), can be written in the following form ($h=$ 0):

The parameters in Eq. (10) have to satisfy relations Eq. (9) as well as the conditions of existence of point transforms ${{\rm T}}_{k+1}$, namely:

Point transform ${\rm T}$ of point ${{\rm M}}_1\in f_1\left({\tau }_1\right)$ into point ${{\rm M}}_{n+1}\in f_1\left({\tau }_{n+1}\right)$ under conditions Eq. (11) is defined as:

5. Existence and stability conditions for fixed points at a point map t corresponding to periodic two-impact motion modes

If $S_i$ is the number of strokes of the $i$th SS against the stopper during one period $f\left(\tau \right)$, and $n$ is multiplicity of period Г of the periodic motion mode to period $f\left(\tau \right)$, then the periodic motion will be characterized by numbers $S_i$, $n(i=$ 1, 2,..., $N)$. It means that the problem of analyzing the periodic motion mode with a single stroke of each of the $N$ SS’s can be reduced to analyzing the properties of point mapping $T$ and the conditions of existence of the latter ($C$-bifurcations), analogous to analyzing systems with discontinuous nonlinearities [18, 19]. Thus, the coordinates of a fixed point ${{\rm M}}^{*}({\tau }^{*},{\dot{{\rm X}}}^{*})$ corresponding to the periodic motion mode with successive strokes of each of the SS’s are determined from system $2\left(N+1\right)$ of Eq. (8) supplemented by periodicity conditions:

Using simple transformations, it can be found from system (8) and (13) that:

where the components of $N$-dimensional vector-function $b(b_1,...,b_N)$ are independent of ${\dot{{\rm X}}}^{*}$, ${\dot{{\rm X}}}_{k+1}$ but are functions of ${\tau }^{*}$, ${\tau }_{k+1}$ and the parameters of the system:

Times ${\tau }_k$, $k=$ 1, 2, 3,..., $N$ are determined by solving the system of nonlinear equations of the form:

Stability in the small of the main of the periodic motion modes depends on the value of the roots of the characteristic equation:

where coefficients $a_l,l=$ 0, 1, 2 are defined, as usual [4], after the linearization of the equations of point transform of $T$ in the vicinity of a fixed point. After some simple transformations one obtains:

where $A\left(Z\right)$, $B$, $C\left(Z\right)$, $D\left(Z\right)$ are square matrices, with non-zero entries having the following form:

Let us consider in a more detail the dynamics of the mechanism for various values of $N$ of SS’s.

6. The dynamics of single piston mechanism

$N=$ 1. Using Eqs. (14-17), the coordinates of the fixed point are determined through the parameters of the system as:

where $\mathrm{\Omega }=\pi np(1-R)/\left(\mu \right(1+R\left)\right)\le 1$, and the coefficients of the characteristic equation are.

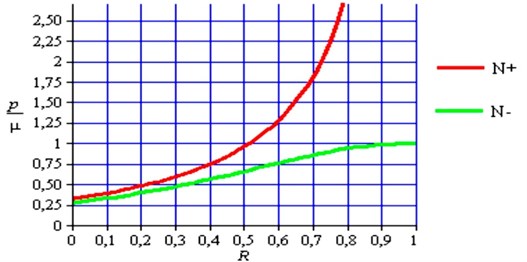
The regions of existence and stability of periodic single-stroke motion modes are limited by surfaces $N_{+}$, $N_{-}$, $N_{\phi }$ whose equations in the parametric form have, respectively, the following form:

Fig. 3 shows subdivision of the parameter plane $\mu /p$, $R$ into the planes (between the upper $N_{+}$ and the lower $N_{-}$ boundaries) of existence and stability of a periodic single stroke $n$-tuple motion mode.

Fig. 3The boundaries of the region of existence and stability

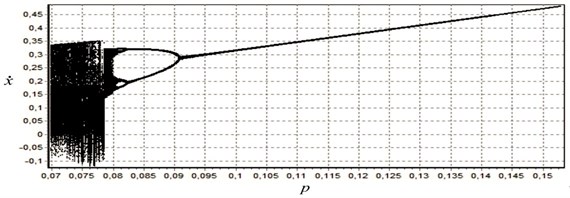
In Fig. 4(a) bifurcation diagram for parameter $p$ is shown for and $\mu =$ 0, 12 wherefrom it follows that a single-stroke motion mode of the mechanism does exist on the interval for the frequency parameter presented in Fig. 3. In the region of the parameters that do not belong to this interval, there exist, as was expected, periodic motions with two (Feigenbaum doubling bifurcation [9]), three, etc. strokes of SS for the period of motion.

Fig. 4The bifurcation diagram for parameter p

It is to be noted that for $N=$ 1°, $f\left(\tau \right)$ is an analytical function and, thus, by substituting variable $y=x-f\left(\tau \right)$ in Eqs. (8), a mathematical model of a conventional impact oscillator is obtained. Its dynamics has been investigated in numerous works (see [4, 5] and the references thereof).

It is known [19] that for $R=$ 0 point mapping Eq. (10) is reduced to analyzing the point mapping of a circle into a circle. In what follows, for a non-monotonous point transform of a circle into a circle, the structure of the boundaries of the existence and stability regions in the large is studied, and the theorem of un-attainability of these boundaries is proved [21, 22].

Consider a point mapping of a circle into a circle:

where nonlinear 1-periodic function $0<f(\tau ,\alpha ,\beta )<{\rm K}(\alpha ,\beta )$, ${\rm K}(\alpha ,\beta )>1$ satisfies the following conditions:

А. Derivative $f_{\tau }^{\text{'}}(\tau ,\alpha ,\beta )$ exists everywhere except, perhaps, $\tau =a<1$, where existence of one-sided derivatives is assumed, as well as in points $\tau =0,\tau =$ 1.

В. $f_{\tau }^{\text{'}}(\tau ,\alpha ,\beta )<0$, $0<\tau \le b<a$, $f_{\tau }^{\text{'}}(\tau ,\alpha ,\beta )>0$, $a<\tau <1$, $f_{\tau \tau }^{\text{'}\text{'}}(\tau ,\alpha ,\beta )>0$, $0<\tau <a$.

C. $f_{\tau }^{\text{'}}(0,\alpha ,\beta )>-2$.

As function $f\left(\tau ,\alpha ,\beta \right)$ is non-monotonous, the mapping of Eq. (19) for $1<f\left(0,\alpha ,\beta \right)<2$ can have simple, only one-turn $\stackrel{-}{\tau }=\tau +1$ fixed points ${\tau }^{*}<a$ and ${\tau }^{**}>a$, the first one always being stable due to conditions B and C, whereas the second one always being unstable. Further, if not specially stated, the case of $1<f(0,\alpha ,\beta )<2$ will be considered. It is to be noted that mapping Eq. (19) is monotonous if ${f\text{'}}_{\tau }^{}(0,\alpha ,\beta )>-1$ (see condition B), and, as $f_{\tau \tau }^{\text{'}\text{'}}>0$ derivative $f_{\tau }^{\text{'}}(\tau ,\alpha ,\beta )$ has in point $\tau =$ 0. Equation ${f\text{'}}_{\tau }(0,\alpha ,\beta )=$ –1 defines in the plane of parameters $\alpha$, $\beta$ boundary ${\mathrm{\Gamma }}_M$ of monotonous transform ${{\rm T}}_{\tau }$.Define the region of the values of parameters $\alpha$, $\beta$, where ${{\rm T}}_{\tau }$ is monotonous through $G_M$.

Coordinates ${\tau }^{*}$, ${\tau }^{**}$ of simple fixed points of mapping Eq. (19) are found from condition $f(\tau ,\alpha ,\beta )=1$ and their boundaries of existence are:

It is evident that equations $f(a,a,\beta )=$ 1, $f(0,\alpha ,\beta )=$ 1 define in the plane of parameters the boundaries of birth and disappearance of the fixed points, respectively. Let $G$ signify the region of existence of fixed mapping points Eq. (19), limited in plane $\alpha$, $\beta$ by Eq. (20).

Based on the above-mentioned properties of function $f(\tau ,\alpha ,\beta )$ and transform ${{\rm T}}_{\tau }$, it can be shown that

1. For $\stackrel{-}{\tau }\left(0\right)<{\tau }^{**}\left(\stackrel{-}{\tau }\right(0)=f(0,\alpha ,\beta )-1)$, despite function ${{\rm T}}_{\tau }$ being non-monotonous, all the points of a unit segment are transformed into a stable fixed point ${\tau }^{*}$, except for ${\tau }^{**}$.

2. For $\stackrel{-}{\tau }\left(0\right)>{\tau }^{**}$, counting number of the points of a unit segment is transformed into an unstable fixed point${\tau }^{**}$.

3. Equation $\stackrel{-}{\tau }\left(0\right)={\tau }^{**}$ in the plane of parameters $\alpha$, $\beta$ defines the bifurcation curve:

Depicting in $G$ the region of stability in the large. In Eq. (21), the value of ${\tau }^{**}$ is determined from $f({\tau }^{**},\alpha ,\beta )=$ 1, where $a<{\tau }^{**}<1$.

Boundary Eq. (21), defined as ${\mathrm{\Gamma }}_{•}$, is shown to be an unreachable boundary, that is, in any of its vicinities there are bifurcation boundaries corresponding to creation of transform points of ${{\rm T}}^n$.

Define $\tau ={\tau }_1^0$ from equation ${\rm T}{\tau }_1^0=$ 0, i.e. ${\tau }_1^0={{\rm T}}^{-1}\left(0\right)$ (under conditions (A, B, C) and for the above mentioned properties of point transform, ${\tau }_1^0$ is defined uniquely).

Consider the sequence of inverse mappings ${{\rm T}}^{-n}\left({\tau }_1^0\right)$ with the values of $\tau$ on the interval $({\tau }^{**},{\tau }_1^0)$. As function $\stackrel{-}{\tau }$ is monotonous on this interval, sequence ${{\rm T}}^{-n}\left({\tau }_1^0\right)$ is defined uniquely.

Let ${{\rm T}}^{-n}\left(0\right)={\tau }_n^0$. From the definition of ${\tau }_n^0$ it follows that ${\tau }^{**}<{\tau }_n^0<{\tau }_1^0$, as well as the evident equalities:

Using relations Eq. (22), as well as conditions A, B, C it is shown that the following lemma holds:

Lemma. If ${\rm T}\left(0\right)={\tau }_{n-1}^0,n\ge 1$, then

1. ${{\rm T}}^n\left({\tau }_i^0\right)={\tau }_i^o$, $i=$ 0, 1, ..., $n-1$, ${\tau }_0^0=$ 0.

2. In points $\tau ={\tau }_i^0(i=\mathrm{0,1},...,n-1)$ the function has local maximum.

Proof. 1. The first assumption directly follows from the equalities:

2. Let $g\left(\tau \right)={{\rm T}}^n\left(\tau \right)$, $n\ge 2$.

Then, for the values of $\tau$ containing a derivative of function $g\left(\tau \right)$, we have:

where:

Let us assume that $U={{\rm T}}^{n-1}\left(\tau \right)$ in points $\tau ={\tau }_i^0(i=\mathrm{0,1},...,n-2)$ has a local maximum ($dU/d\tau$ may not exist in these points). As $U_i^0=U\left({\tau }_i^0\right)={{\rm T}}^{n-1}\left({\tau }_i^0\right)={{\rm T}}^{-1}\left({\tau }_i^0\right)={\tau }_{i+1}^0$ if the conditions of lemma hold, then, due to (A), $dT(U=U_i^0)/dU>0$. Hence, $\tau ={\tau }_i^0$$(i=\mathrm{0,1},...,n-2)$ are points of local maximum for transform ${{\rm T}}^{n-1}\left(\tau \right)$.

Let $\tau ={\tau }_{n-1}^0$. Then $U\left({\tau }_{n-1}^0\right)={{\rm T}}^{n-1}\left({\tau }_{n-1}^0\right)=$ 0, i.е. $dT/dU$ changes its sign after crocking this point. But, in this case $dU(\tau ={\tau }_{n-1}^0)/d\tau >0$ because for $1\le i\le n-2$ there is ${\tau }^{**}<{{\rm T}}^i{\tau }_{n-1}^0<{\tau }_1^0$ .

Thus, if $U={{\rm T}}^{n-1}\left(\tau \right)$ has local maximums in points ${\tau }_i(i=\mathrm{0,1},...,n-2)\text{,}$ then $g\left(\tau \right)={{\rm T}}^n\left(\tau \right)$ also has local maximums in points $\tau ={\tau }_i^0(i=\mathrm{0,1},...,n-1)$. Keeping in mind that $\stackrel{-}{\tau }={\rm T}\tau$ has a local maximum in point $\tau =$ 0, induction provides a proof of the lemma.

Corollary. Condition:

Defines on the plane of parameters a bifurcation curve corresponding to the creation of $n$ fixed points $\tau ={\tau }_i^0(i=\mathrm{0,1},...,n-1)$ of mapping ${{\rm T}}^n\left(\tau \right)$, i.е. to the creation of a cycle of $n$-tuple mapping points ${\rm T}\tau$.

The bifurcation curve on the plane of parameters that corresponds to the appearance of fixed mapping points of ${{\rm T}}^n\tau$ under condition Eq. (23) will be denoted by ${\mathrm{\Gamma }}_n$. The equation of this curve is:

Comparing the equations of bifurcation curves ${\mathrm{\Gamma }}_n$ and of curve ${\mathrm{\Gamma }}_{•}$ and also bearing in mind relation Eq. (23), one can postulate.

Theorem. For any $\epsilon >0$, there exists natural $N$, such that, for any $n>N$, bifurcation curves ${\mathrm{\Gamma }}_n$ lie in the plane of parameters $\alpha$, $\beta$ in $\epsilon$ the vicinity of curve ${\mathrm{\Gamma }}_{*}$. ${\mathrm{\Gamma }}_{*}$ – unreachable boundary.

Comment 1. An unreachable boundary exists even for more general assumptions, in particular, without limitations on the sign of ${f\text{'}\text{'}}_{\tau \tau }(\tau ,\alpha ,\beta )$ and without condition $C$.

Comment 2. If $f(\tau ,\alpha ,\beta )$ is an analytical function then, after crossing bifurcation boundary ${\mathrm{\Gamma }}_n$ two cycles of $n$-tuple points are created: a stable one and a non-stable one, i.е. in this case any vicinity of curve ${\mathrm{\Gamma }}_{*}$ comprises an even number of stability regions of cycles of multiple points.

Comment 3. However, in realistic systems, $g\left(\tau \right)$ is normally a smooth nonlinear function. Then, evidently, boundary ${\mathrm{\Gamma }}_{*}$ will also be unreachable, and after crossing each of ${\mathrm{\Gamma }}_n$ cycles of $n$-tuple points will be created, one of them being stable. In this case, ${\mathrm{\Gamma }}_{*}$ is boundary of capture [24, 25], region $G$ is region of stability in the large of the main mode, for adjusting and maintaining of which parameters $\alpha$, $\beta$ are to be chosen in such a way that, if they change, conditions of technological stability was provided [26, 27], or distance $\rho (M,{\mathrm{\Gamma }}_{*})$ of the working point ${\rm M}({\alpha }^{*},{\beta }^{*})$ from ${\mathrm{\Gamma }}_{*}$ was considerably larger than $\epsilon$. Boundary ${\mathrm{\Gamma }}_{*}$ in this case is dangerous [28, 29].

Comment 4. It is to be noted that for certain conditions imposed on $f(\tau ,\alpha ,\beta )$ one can absolutely analogously consider regions of existence of m-revolution simple fixed points, investigate their stability and write an equation of the curve analogous to ${\mathrm{\Gamma }}_{*}\left(m\right)\left(\stackrel{-}{\tau }\right(0)={\tau }^{**}-m)$. In doing so it is easily shown that boundaries ${\mathrm{\Gamma }}_{*}\left(m\right)$, $m=$ 1, 2, …. are unreachable.

7. Conclusion

The work describes:

– a model of a new multi-striker eccentric shock-vibration mechanism with a crank-sliding bar vibration exciter and an arbitrary number of pistons;

– the phase space of the mathematical model;

– equations of a general (for a random number of SS) point mapping of a two-dimensional non-analytical intersecting surface into itself;

– equations (in the parametric form) of the coordinates of the fixed points corresponding to periodic motions with alternating strokes of each of the SS’s;

– bifurcation boundaries of existence of the above mentioned equations of point mappings.

The main results achieved:

– a methodology and algorithms of constructing point mapping equations of non-analytical secant surfaces truncated along phase coordinates have been developed;

– the parameter space has been subdivided into regions of stability of periodic motion modes;

– the study of dynamics of a single-piston mechanism undergoing a perfectly inelastic collision has been formulated as a Poincare map of a circle into itself;

– the existence of a denumerable number of stable periodic modes of motion in the neighborhood of unreachable boundaries in the extended phase space has been proven;

– bifurcation values of the parameters have been demonstrated, for which chaotic motion modes exist. The scenario of the appearance of chaotic motion modes is very similar to the scenario of doubling of Feigenbaum period [23-28].