Influence of asymmetric structure parameters on rolling mill stability

2.1. Structure model and modal analysis

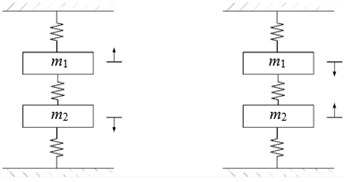
For a typical four-high mill, in order to facilitate the analysis, the upper-system and sub-system are simplified as ones with a single degree of freedom respectively. It is assumed that the mill vibrates up and down along the vertical direction. The asymmetric structure model of rolling mill is illustrated in Fig. 1.

Fig. 1Simplified asymmetric structure model

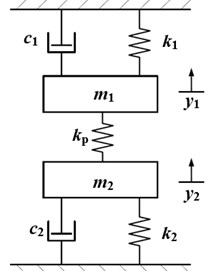
This paper establishes an asymmetric model by extending the vertical model from literature [4]. The asymmetric model which considers the difference of structure parameters between the system upper and lower parts can be used to study the asymmetric vibration phenomenon and the influence of asymmetric parameters on the system stability. As shown in Fig. 1, $m_1$is the lumped equivalent mass of the top roll, top backup roll and upper mill housing, which is simplified to the center of the top work roll. $m_2$ is the lumped equivalent mass of the bottom roll, bottom backup roll and lower mill housing, which is simplified to the center of the bottom work roll. $k_1$, $c_1$ are the vertical equivalent stiffness and vertical damping due to support from the upper frame and the upper beam of the rolling mill. $k_2$, $c_2$ are the vertical equivalent stiffness and vertical damping due to the support from lower frame and the lower beam of the rolling mill. $k_p$ is the equivalent stiffness of strip deformation during vibration. $y_1$, $y_2$ are displacements of the vertical vibration from upper rolls and lower rolls respectively. $F_{var}$ is the variation of rolling force.

This paper uses the structural parameters from literature [4] to analyze the natural frequencies and mode shapes of the system. The selected structural parameters are shown in Table 1, the natural frequencies and mode shapes of the system are shown in Table 2.

It can be seen from Fig. 2, the upper and lower rolls system vibrates in the same direction at the first-order natural frequency, which is called the same direction vibration modal. The upper and lower rolls system vibrates in the reverse direction at the second-order natural frequency, which is called the reverse direction vibration modal. The reference [4] can only demonstrate a study of the reverse direction modal for the symmetric assumption. As compared with the reference [4], the asymmetric model can be used to study either the reverse direction vibration mode of the system, or the same direction vibration mode of the system, avoiding the loss of the vibration mode. This model is the basis for studying the effect of asymmetric parameters on the rolling mill stability.

Fig. 2a) Vibration mode under first-order natural frequency, b) vibration mode under second-order natural frequency, c) same direction vibration schematic diagram, d) reverse direction vibration schematic diagram

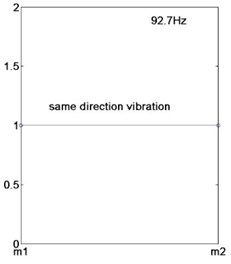
a)

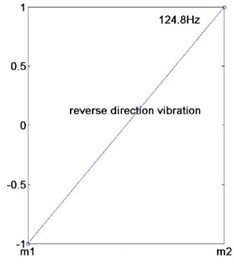
b)

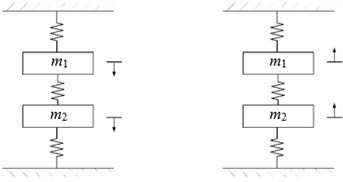
c)

d)

2.2. Dynamic model of rolling process

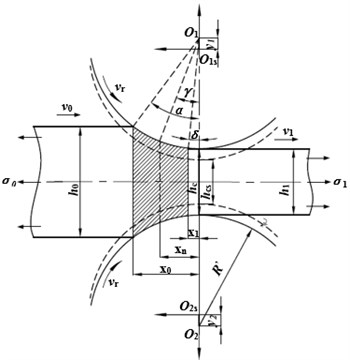
The geometry of the roll bite is illustrated in Fig. 3, where $O_{1s}$ and $O_{2s}$ are the original geometrical centers of the top and bottom rolls (before vibration begins). $O_1$ and $O_2$ are the ever-changing centers of the rolls. $h_0$ and $h_1$ are the strip thicknesses at the inlet and outlet. $h_c$ isthe roll gap spacing measured along the centerline $O_1{O}_2$, $h_{cs}$ isthe roll gap spacing measured along the centerline $O_{1s}{O}_{2s}$. $\alpha$ is the inlet angle, $\alpha =\mathrm{s}\mathrm{i}\mathrm{n}\alpha =\sqrt{(h_0-h_c)/R^{\text{'}}}$. $\gamma$ is the neutral angle. $\delta$ is the outlet angle, $\delta =\mathrm{s}\mathrm{i}\mathrm{n}\delta =x_1/R^{\text{'}}$. $l$ is the horizontal projection length of the contact arc, $l=x_1-x_0$. $R$ and $R^{\text{'}}$are the radiuses of the original work roll and deformed work roll. ${\sigma }_0$ and ${\sigma }_1$ are the strip tensile stresses at the inlet and outlet. $v_0$ and $v_1$ are the strip velocities at the inlet and outlet. $v_r$ is the roll peripheral velocity. $x_0$, $x_n$ and $x_1$ are the inlet position, neutral position and outlet position measured from the centerline $O_{1s}$, $O_{2s}$. And it is assumed that the strip width at the inlet and outlet are $B$.

Zeng et al. [4] assumed that the model is symmetrical, so it is only valid to study symmetrical vibration of the rolling mill. In this paper, the model is asymmetric and the vibration of upper and lower rolls is asymmetrical, so the equation $h_c=h_{cs}+2y_c$ in [4] is replaced with the Eq. (1):

The Hill simplified formula of Bland-Ford rolling force model is as follows [6]:

where, ${\sigma }_m$ is the mean tensile stress, usually considered as ${\sigma }_m=0.7{\sigma }_0+0.3{\sigma }_1$. $Q_p$ is the stress state factor, $Q_p=1.08+1.79\epsilon \mu \sqrt{R^{\mathrm{\text{'}}}/h_0}-1.02\epsilon$. $\epsilon$ is the reduction ratio, $\epsilon =(h_0-h_1)/h_0$. $K$ is the mean deformation resistance, $K=A\cdot {{\epsilon }^n}_{{\sum }_m\mathrm{‍}}$. $A$ and $n$ are the coefficients associated with the strip carbon content. ${\epsilon }_{{\sum }_m\mathrm{‍}}$ is the mean total deformation extent, ${\epsilon }_{{\sum }_m\mathrm{‍}}=b_0{\epsilon }_0+b_1{\epsilon }_1$. ${\epsilon }_0$ is the total deformation extent at the inlet of this mill stand, ${\epsilon }_0=(H-h_0)/H$. ${\epsilon }_1$ is the total deformation extent at the outlet of this mill stand, ${\epsilon }_1=(H-h_1)/H$. $H$ is the initial strip thickness at the inlet of the first mill stand in a configuration. $b_0$ and $b_1$ are coefficients, usually considered as $b_0=$ 0.4, $b_1=$0.6.

According to the relationship in the rolling deformation zone, the rolling force acting on rolls in the vertical direction is given by:

The strip velocities at the inlet and outlet, the strip inlet position, outlet position and neutral position can be obtained based on the geometry of the roll bite, as well as on the metal flow equation and equilibrium conditions of the force in the deformation zone, as shown in Eq. (4):

From Eq. (2), (3) and (4), the rolling force acting on the rolls, the strip velocities at the inlet and outlet can be implicitly formulated as a function in terms of the following variables, i.e.:

Fig. 3Roll bite geometry during vibration

Since the chatter phenomenon in rolling is considered as a dynamic phenomenon rather than a static one, it is more important to study the variations of the system parameters rather than their steady-state values [3]. The variation of $F$, $v_0$ and $v_1$ can be obtained by utilizing the first-order Taylor expansion [1, 3, 4]:

where, $h_{cvar}=y_1-y_2$, ${\dot{h}}_{cvar}={\dot{y}}_1-{\dot{y}}_2$.

$a_{F,{\sigma }_0}$, $a_{F,{\sigma }_1}$, $a_{F,h_0}$, $a_{F,h_c}$, $a_{F,h_c}$, are the partial derivatives of $F$ with respect to ${\sigma }_0$, ${\sigma }_1$, $h_0$, $h_c$, ${\dot{h}}_c$, respectively. These coefficients characterize the impact factors of the variation of ${\sigma }_0$, ${\sigma }_1$, $h_0$, $h_c$, ${\dot{h}}_c$ on the variation of $F$, $a_{v_0,{\sigma }_0}$, $a_{v_0,{\sigma }_1}$, $a_{v_0,h_0}$, $a_{v_0,h_c}$, $a_{v_0,{\dot{h}}_c}$are the partial derivatives of $v_0$ with respect to ${\sigma }_0$, ${\sigma }_1$, $h_0$, $h_c$, ${\dot{h}}_c$, respectively. These coefficients characterize the impact factors of the variation of ${\sigma }_0$, ${\sigma }_1$, $h_0$, $h_c$, ${\dot{h}}_c$ on the variation of $v_0$. $a_{v_1,{\sigma }_0}$, $a_{v_1,{\sigma }_1}$, $a_{v_1,h_0}$, $a_{v_1,h_c}$, $a_{v_1,{\dot{h}}_c}$ are the partial derivatives of $v_1$ with respect to ${\sigma }_0$, ${\sigma }_1$, $h_0$, $h_c$, ${\dot{h}}_c$, respectively. These coefficients characterize the impact factors of the variation of ${\sigma }_0$, ${\sigma }_1$, $h_0$, $h_c$, ${\dot{h}}_c$on the variation of $v_1$.

All the calculations of coefficients in Eq. (6) are given in Appendix.

A change of the roll gap caused the fluctuation of the strip velocity, and then resulted in the fluctuation of the strip tensile stress. The tensile stress variation at the inlet and outlet can be expressed as:

where, $E$ is the Young’s modulus of the strip. $L_0$ and $L_1$ are distances from this stand to the upstream stand and downstream stand.

2.3. Mathematical model of rolling vibration

Equilibrium equation of vibration system can be written as:

As Eq. (7) has the integral terms of time, Eq. (7) is taken as a derivative with respect to time.

By combining the structure modal with dynamic model of rolling process, we can get the mathematical rolling chatter model:

In order to analyze the system stability, the Eq. (10) is written as the Eq. (11) which is the first-order algebraic equation combined with the Eq. (6) and Eq. (7), and using ${\left(x_1,x_2,x_3,x_4,x_5,x_6\right)}^T$ to substitute ${\left(y_1,{\dot{y}}_1,y_2,{\dot{y}}_2,{\sigma }_{0var},{\sigma }_{1var}\right)}^T$:

And the mathematical model of rolling vibration is expressed as a first-order differential equation in the matrix form:

where:

4.1. Mathematical model of the rolling vibration

4.1.1. Stability analysis under asymmetric stiffness

In this section, the influence of upper and lower stiffness ratio on the stability of rolling mill system is analyzed under the condition of constant natural stiffness. So, let us assume that $c_2=c_1$, $m_2=m_1$. The necessary and sufficient condition for a linear time-invariant system to be stable is that all the system eigenvalues or the roots of the characteristic equation possess a negative real part. As shown in Eq. (13), the characteristic matrix of the mathematical model is a six-order square, and the elements of the characteristic matrix are generally represented by complex mathematical relationships of rolling process parameters. Thus, it is difficult to achieve the eigenvalue of the system in a symbolic or analytical form. However, it is rather easy to calculate the eigenvalue with a numerical method. If all the eigenvalues have the negative real part, the system is stable, if not, the system is unstable. The result is illustrated in Fig. 4.

As shown in Fig. 4, the full line shows the critical speeds under different stiffness ratios. It is observed that the figure is symmetrical about ${\zeta }_k=$ 0, which means the system stability is the same when $k_2/k_1=k_1/k_2$, so the paper has just analyzed the right half of the figure. It is observed that the system unstable critical line is spliced by Line I and Line II. For a further analysis of the system dynamics, two points (point A, point B) are taken on Line I and Line II randomly. The eigenvalue and instability type of the two points and their neighborhood are shown in Table 4.

Fig. 4Influence of stiffness ratio on system stability under constant natural stiffness

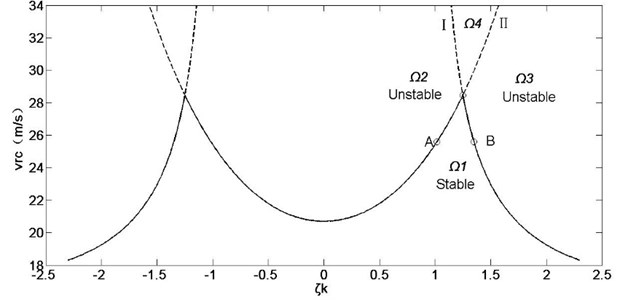
Table 4Eigenvalue and instability type of point A, point B and their neighborhood

$v_r$ / (m/s)	${\zeta }_k$		${\lambda }_{\mathrm{1,2}}$ (×102)	${\lambda }_{\mathrm{3,4}}$ (×102)	${\lambda }_5$ (×102)	${\lambda }_6$ (×102)	Instability type
25.61	A–	1.008	0.005±9.43i	–0.137±5.95i	–3.503	–1.500	Reverse direction instability
	A	1.018	0.000±9.45i	–0.133±5.96i	–3.503	–1.501	Stable
	A+	1.028	–0.004±9.47i	–0.129±5.96i	–3.503	–1.501	Critical stability
	B–	1.337	–0.136±10.23i	–0.004±6.00i	–3.490	–1.499	Stable
	B	1.347	–0.140±10.26i	0.000±6.00i	–3.490	–1.499	Critical stability
	B+	1.357	–0.144±10.29i	0.004±6.00i	–3.489	–1.499	Same direction instability

As it can be seen from Table 4, at the rolling speed of 25.61 m/s, all the eigenvalue of the system has the negative real part when ${\zeta }_k>$1.018, what means the system is stable at the moment. When ${\zeta }_k=$ 1.018, a pair of pure imaginaries appears in the system, and this pair of conjugate eigenvalue ${\lambda }_{\mathrm{1,2}}$ represents the characteristic of the same direction modal defined in section 2.1, what means the system is in the critical state this time. However, when ${\zeta }_k<$1.018, the real parts of eigenvalue ${\lambda }_{\mathrm{1,2}}$ becomes positive, in other words, the same direction vibration modal loses its stability. Therefore, Line I is the critical boundary of the same direction vibration modal. Similarly, Line II is the critical boundary of the reverse direction vibration modal. Line I, Line II and ${\zeta }_k$ coordinate axis form the region ${\mathrm{\Omega }}_1$, where the system is stable. The system is unstable in other regions.

As it can be seen from the above analysis, when the stiffness difference in upper and lower parts is small, the stable domain in the system is determined by Line I. At the lower side of Line I the system is stable, and the system is unstable and vibrates in the reverse direction at the upper side of Line I. However, when the stiffness difference in upper and lower parts is large, the stable domain in the system is determined by Line II. At the lower side of the Line II, the system is stable, and the system is unstable and vibrates in the same direction at the upper side of Line II. There is an optimal stiffness distribution ratio at the intersection of two lines, namely ${\zeta }_k=$ 1.247, where the mill system is the most stable. In these three regions around the optimal stiffness ratio, the system vibration modal is different, and there is a modal conversion phenomenon there. On the left of the optimal stiffness ratio, the region ${\mathrm{\Omega }}_2$, which is enclosed by Line I and Line II, is unstable and vibrates in the reverse direction. On the right of the optimal stiffness ratio, the region ${\mathrm{\Omega }}_3$ which is enclosed by Line I and Line II is unstable and vibrates in the same direction. Above the optimal stiffness ratio, the region ${\mathrm{\Omega }}_4$, which is enclosed by Line I and Line II, is unstable with two modes.

4.1.2. Dynamic response at unstable points

Moreover, in order to verify the correctness of the system stability analysis, the system motions corresponding to the unstable point A– and point B+ are numerically simulated. For an initial disturbance $y_1=$ 10^-6m, the simulation results are shown in Figs. 5-6. And the time domain from 3.98 s to 4 s is taken to compare the instability types of $y_1$ and $y_2$ in Fig 7.

Fig. 5Dynamic system response at A– for ζk= 1.008, vr= 25.61 m/s

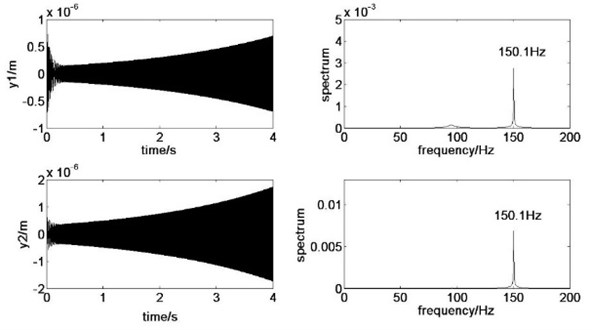
Fig. 6Dynamic system response at B+ for ζk= 1.357, vr= 25.61 m/s

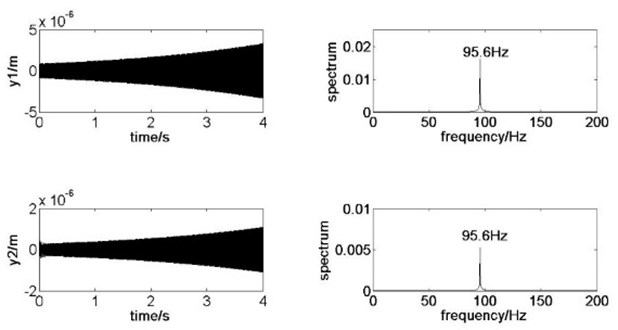
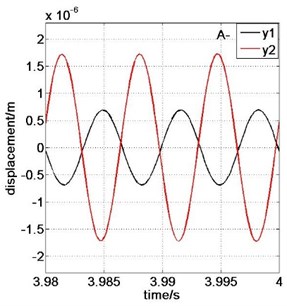
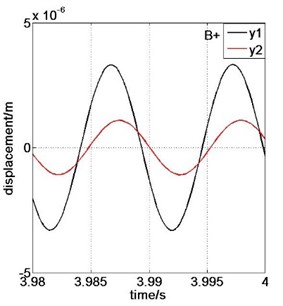
Fig. 7Displacement contrast for y1 and y2: a) A– point, b) B+ point

a)

b)

As shown in Fig. 5, the system is unstable and vibrates with the second-order natural frequency at the condition of ${\zeta }_k=$ 1.008, $v_r=$ 25.61 m/s. As shown in Fig. 7, the upper rolls and lower rolls vibrate in the reverse direction. Therefore, the system is unstable with the reverse direction vibration modal. As shown in Fig. 6, the system is unstable with the first-order natural frequency at the condition of ${\zeta }_k=$ 1.357, $v_r=$ 25.61 m/s. As shown in Fig. 7, the upper rolls and lower rolls vibrate in the same direction. Therefore, the system is unstable with the same direction vibration modal. The calculation results and analysis conclusions in section 4.1.1 were proved to be correct.

4.1.3. Influence of asymmetric stiffness on the rolling mill stability under different structural parameters

In order to analyze the effect of asymmetric stiffness on the rolling mill stability under different structural parameters, the system stability is studied under different natural stiffness value, mass value and damping value, respectively. The simulation results are shown in Fig. 8-10.

Fig. 8Influence of asymmetric stiffness on the rolling mill stability at different natural stiffness

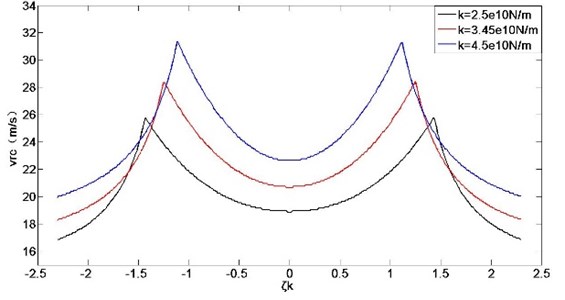
Fig. 9Influence of asymmetric stiffness on the rolling mill stability at different mass

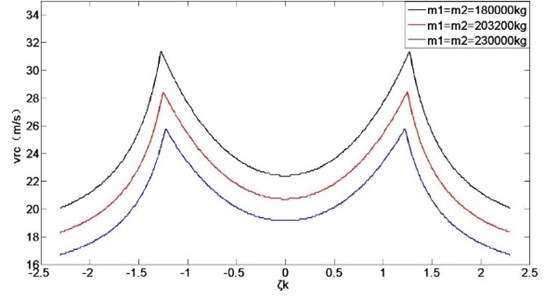
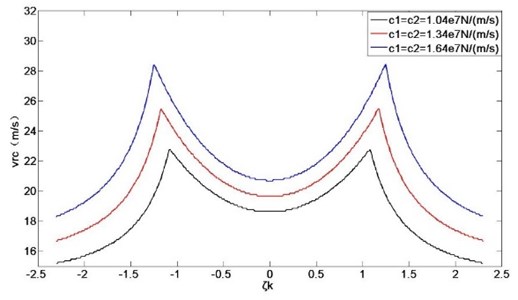
As shown in Figs. 8-10, with increasing of the natural stiffness and mass, the optimal stiffness ratio gets smaller. With the damping increase, the optimal stiffness ratio gets bigger. However, with the change of natural stiffness value, mass value and damping value, the influence rule of stiffness ratios on the mill system stability has not changed, it only changes the position of the optimal stiffness ratio. The stiffness ratio of the rolling mill can be adjusted appropriately under the premise of meeting the other design requirements to obtain the optimal stiffness ratio, which makes the rolling mill system more stable.

Fig. 10Influence of asymmetric stiffness on the rolling mill stability at different damping

4.2. Stability analysis and dynamic response under asymmetric mass

In this section, the influence of mass ratio on the stability of rolling mill system is analyzed under the condition of constant total mass, by assuming that $k_2=k_1$, $c_2=c_1$.

Fig. 11Influence of mass ratio on system stability under constant total mass

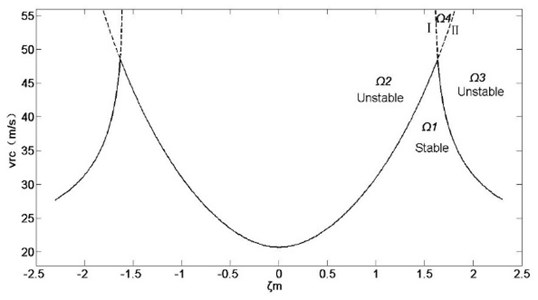
As shown in Fig. 11, the influence of asymmetric mass on the system stability is similar to the asymmetric stiffness. Specific analysis methods and procedures are described in section 4.1.1, so we do not repeat them here. The full line shows the critical speeds under different mass ratios. Line I, Line II and ${\zeta }_m$ axis form the region ${\mathrm{\Omega }}_1$, where the system is stable. The system is unstable in other regions. When the mass difference in upper and lower parts is small, the stable domain in the system is determined by Line I. At the lower side of Line I the system is stable, and the system is unstable and vibrates in the reverse direction at the upper side of Line I. However, when the mass difference in asymmetry upper and lower parts is large, the stable domain in the system is determined by Line II. At the lower side of Line II the system is stable, and the system is unstable and vibrates in the same direction at the upper side of Line II. There is an optimal mass distribution ratio at the intersection of two lines, namely ${\zeta }_m=$ 1.627, where the mill system is the most stable. In three regions around the optimal mass ratio, the system vibration modal is different, and there is a modal conversion phenomenon. On the left of the optimal mass ratio, the region ${\mathrm{\Omega }}_2$, which is enclosed by Line I and Line II, is unstable and vibrates in the reverse direction. On the right side of the optimal mass ratio, the region ${\mathrm{\Omega }}_3$, which is enclosed by Line I and Line II, is unstable and vibrates in the same direction. Above the optimal mass ratio, the region ${\mathrm{\Omega }}_4$, which is enclosed by Line I and Line II, is unstable in two modes.

Under the condition of structural parameters changing, the effect of asymmetric mass on the rolling mill stability is in line with the effect of asymmetric stiffness on the rolling mill stability. With the change of stiffness value, total mass value and damping value, the influence rule of mass ratios on the mill system stability has not changed. It only changes the position of the optimal mass ratio. The mass ratio of the rolling mill can be adjusted appropriately under the premise of meeting other design requirements to obtain the optimal mass ratio, which makes the rolling mill system more stable.

The results verify that asymmetric structure parameters have a significant impact on the system stability and critical conditions. And the study of the influence of asymmetric structure parameters on the rolling mill stability will help us to study the vibration modes of the rolling mill more comprehensive. It is necessary to consider the asymmetry of mill structure, and it can provide a guidance for dynamic system structure modifications and mill optimization design.