Abstract
The paper considers a new technique for increasing the dynamic stability of the dynamics of milling flexible parts. The technique is based on the formation of a uniform stock of the workpiece for the finish milling. The paper proposes an optimization algorithm for the automated calculation of the stock distribution based on the sensitivity analysis method. The ratio of the natural frequencies of the flexible workpiece is used as the objective function of the optimization algorithm. The developed technique was tested on a numerical example.
1. Introduction
Ensuring vibration stability of finish milling of flexible parts is one of the most complicated problems of machining. Due to the intermittent character of cutting and high nonlinearity of the process, vibrations excite in the “workpiece-tool” system. From the point of view on machined surface quality and cutting process productivity, chatter vibrations are the most dangerous. Chatter occurs due to the so-called regenerative effect [1]-[3]. For certain combinations of process parameters, the process may lose of dynamic stability. The loss of dynamic stability of the process is accompanied by increased cutting forces, vibration amplitudes, resulting in vibration scratch on the surface of the processed workpiece, and increased wear of the cutter and machine tool parts.
Currently, several approaches are used to ensure vibration stability of milling [2]: analytical and numerical stability analysis methods [4]-[7], [20]; time integration of equations of motion of the system during milling [8]-[11], [19]; damping of vibrations based on improving individual machine tool parts capable of influencing the dynamic performance of the “tool-part” system as a whole [12], [13]; methods of online detection of chatter using systems with feedback [2], [3].
This paper proposes an alternative method of ensuring vibration stability of milling dynamics based on the automated selection of the workpiece stock for finish milling of flexible parts. Design of variable stock allows ensuring dynamic properties of the workpiece in terms of vibration stability for the given spindle speed range. The special feature of the method is the solution of the optimization problem using sensitivity analysis with the goal function being the ratio of the eigenfrequencies of the system.
2. Method of choosing the goal function for the algorithm of stock optimization
The choice of the target value of the goal function for the proposed optimization approach is based on experience and results obtained from the investigation of the influence of dynamic characteristics of the “tool-workpiece” system on stability margins at steady-state milling motion. For example, in [14], [15], it was established that increasing eigenfrequency, stiffness, and modal damping of the systems leads to the shift of stability margins in the direction of increasing spindle speed and axial cutting depth.
Another characteristic feature of milling dynamics is related to the behavior of stability margins of the steady-state motion of the “tool-part” system with an increase in the number of considered degrees of freedom (DOFs). Paper [16] shows that an approximate stability lobe diagram for a 2DOF system can be obtained by superposition of stability margins of 1DOF systems. So, based on the results presented in [14]-[16], one can establish that position of milling stability margins for systems with several DOFs is not only determined by the values of dynamic characteristics but also by their ratio.
Within the problem of improving vibration stability of finish milling of flexible parts, the optimal ratio of workpiece lower eigenfrequencies defining the position of stability margins in the set cutting parameters’ range can be determined most accurately. For the qualitative assessment of the optimal value of the system eigenfrequencies, it is convenient to use an alternative representation of the stability lobes diagram where the -axis represents the dimensionless frequency of the passage of the tool cutting edges (the value is inversely proportional to the spindle speed):
where, is the -th eigenfrequency of the system, Hz, is the spindle speed, rpm, is the number of cutting edges in the milling cutter.
Using an alternative representation of the stability diagram allows demonstrating the position of stability margins near zones where the dimensionless frequency is even [15]. Given the superposition principle for the increased number of DOFs, one can formulate the milling vibration stability criterion, that ensures at certain values of the spindle speed the superimposition of stability zones associated with the and natural frequencies of the workpiece:
where, , are dimensionless frequencies of the passage of the tool cutting edges (relative to -th and -th system eigenfrequencies), [1.05…1.25].
3. Algorithm of optimizing allowance for finish milling
The method of optimizing dynamic characteristics of the workpiece proposed in this paper is based on FEM simulation in conjunction with the sensitivity analysis method [17]. Optimization design parameters include thicknesses of finite elements of the workpieces determining the workpiece stiffness distribution and, consequently, values of eigenfrequencies. In this case, the main expression for sensitivity analysis can be formulated as follows:
where, is a vector of thicknesses of finite elements of the workpiece at the -th iteration of the optimization algorithm, is the Moore-Penrose pseudoinverse matrix of sensitivity coefficients of model eigenfrequencies to the change of thickness of the finite element, is the of the difference between calculated and desired values of the part eigenfrequencies, ensuring the realization of criterion Eq. (2).
The matrix of the sensitivity coefficients looks as follows:
where, is the number of finite elements in the model, is the number of considered eigenfrequencies, is the sensitivity coefficient of the -th eigenfrequency of the system to the change of thickness of the -th finite element.
The sensitivity coefficient is calculated as follows [17]:
where, is the -th modal mass of the system, is the model eigenmode vector corresponding to the -th eigenfrequency, is the partial derivative of the global stiffness matrix with respect to the thickness of the -th finite element, is the partial derivative of the global mass matrix with respect to the thickness of the -th finite element.
Let us consider the case of optimizing the law of stock distribution for the two lower eigenfrequencies of the workpiece. Then the matrix equation Eq. (3) can be reduced to the following system of equations:
or:
where ; ;
Let us complement the system Eq. (7) with an expression characterizing the target value of the ratio of eigenfrequencies for the allowance optimization problem (see section 2):
where, is the range of acceptable values of ratio of the system eigenfrequencies.
Then the final expression for the optimization algorithm is given by Eq. (9):
where, .
Matrix Eq. (9) allows iteratively formulate the stock distribution for the workpiece so that the optimal ratio of the workpiece eigenfrequencies from the standpoint of milling vibration stability is acquired.
4. Approbation of the optimization algorithm
This section considers an example of optimizing the law of the change of stock for finish workpiece milling based on the results of modeling dynamic of up milling of a flexible plate by a rigid instrument in the 3DCUT software [18]. FEM model of the workpiece, tool trajectory and its cutting edges in the initial moment of time and feed directions are shown in Fig. 1. The cut up milling is considered. The parameters of the finite element model of the workpiece and the geometry of the tool are given in the Tables 1-2.
For the chosen combination of the workpiece material and mill geometry, the coefficients of the phenomenological model of cutting forces were identified according to the calculation and experimental method described in [10]. In this work, a linear model of cutting forces is used:
where , , are the coefficients of the cutting force model characterizing forces of metal deformation; , , are the coefficients of elastic deflection of the material and the friction between the rear edge of the cutting edge and the surface processed. Table 3 presents the values of the cutting force coefficients.
Fig. 1FEM model of the workpiece, tool trajectory for the cut up milling at the free end of the test plate
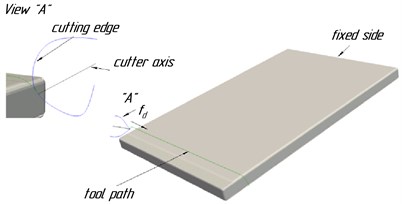
Table 1Parameters of the finite-element model of the workpiece
FE type | Node count | Element count | Material | , MPa | , kg/mm3 | |
QUAD4 | 12354 | 12110 | Aluminum | 72000 | 0.33 | 2.66* |
Table 2Geometrical parameters of the mill
Mill type | Radius, mm | Number of flutes | Helix angle, |
Conical ball mill | 3 | 2 | 45 |
Table 3Values of cutting force coefficients
, N/mm | , N/mm | , N/mm | , N/mm2 | , N/mm2 | , N/mm2 |
1178.24 | 425.84 | 233.40 | 6.83 | 6.44 | 1.33 |
In this case, the dynamics of the cutting tool is not considered, because the mill is much stiffer compared to the part processed, which is characteristic for milling thin-wall flexible details.
Parameters of the process modes of the multivariate calculation are given in Table 4.
Table 4Parameters of the processing modes for the multivariate calculation
, mm/tooth | Stock, mm | |
3.0-4.0 with step of 0.05 | 0.05 | 0.25 |
For this case, the optimization problem is to ensure vibration stability of the milling process for high spindle speeds (equivalent to the range of variation of from 3.05 to 3.25). Fig. 2 shows the comparison of the distribution of thicknesses of finite elements of the plate model before and after optimization.
To demonstrate the effect of the presented method, Fig. 3 shows the diagrams of maximum cutting forces vs. path coordinate and spindle speed. The diagrams were obtained from multivariate modeling of the dynamics of milling the plate before and after optimization.
Also, in Fig. 4 the amplitudes of workpiece vibrations before and after optimization are compared, while Fig. 5 shows a section of the plate surface after milling for the mode with 3.2.
Fig. 2Distribution of workpiece stock
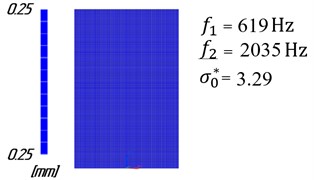
a) Before optimization
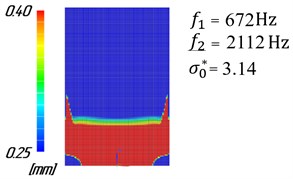
b) After optimization
Fig. 3Diagrams of the cutting force amplitudes
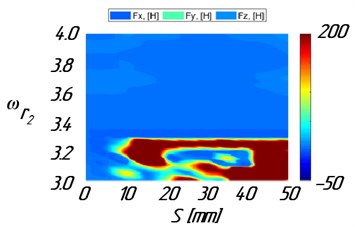
а) Before optimization
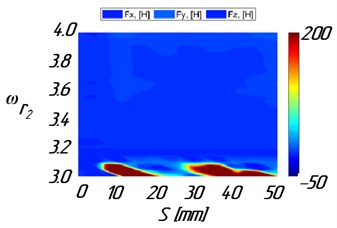
b) After optimization
Fig. 4Time history of vibration amplitudes for ωr2= 3.2
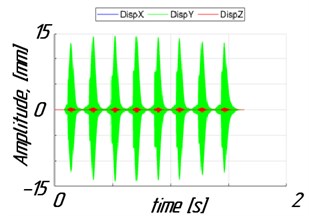
а) Before optimization
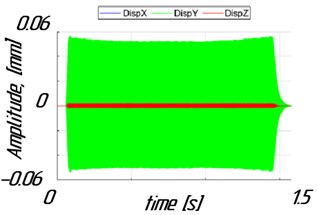
b) After optimization
Fig. 5The surface geometry of the processed part for ωr2 = 3.2

а) Before optimization

b) After optimization
The modeling results show, that for constant stock, chatter vibrations occur in the area of high spindle speeds ( from 3.05 to 3.25). Chatter vibrations result in a significant increase of the cutting forces, Fig. 3(a), and plate vibration amplitudes, Fig. 4(a), leading to vibration marks, Fig. 5(a). Uneven distribution of stock calculated using the algorithm has led to increased workpiece stiffness. Besides, there has been a significant reduction of the cutting force amplitudes, Fig. 3(b), and amplitudes of workpiece vibrations, Fig. 4(b), in the area of high spindle speeds. So, the high surface finish quality of the part can be obtained, Fig. 5(b).
5. Conclusions
This paper described a method of automated calculation of uniform stock ensuring vibration stability of finish milling of flexible parts. The uniform stock can be generated by machining the corresponding target workpiece geometry in the roughing and semi-finishing stages. The method is successfully verified on a numerical experiment of flexible plate finish milling. Further development of the method will be aimed at generalizing the optimization algorithm, taking into account the natural change in the dynamic characteristics of the flexible workpiece in the process of stock removing.
References
-
Quintana G., Ciurana J. Chatter in machining processes: A review. International Journal of Machine Tools and Manufacture, Vol. 51, Issue 5, 2011, p. 363-376.
-
Caixu et al. Y. U. E. A review of chatter vibration research in milling. Chinese Journal of Aeronautics, Vol. 32, Issue 2, 2019, p. 215-242.
-
Faassen R. Chatter prediction and control for high-speed milling. Eindhoven, Netherlands, Eindhoven University of Technology, 2007.
-
Merdol S. D., Altintas Y. Multi frequency solution of chatter stability for low immersion milling. Journal of Manufacturing Science and Engineering, Vol. 126, Issue 3, 2004, p. 459-466.
-
Insperger T., Stépán G. Semi‐discretization method for delayed systems. International Journal for Numerical Methods in Engineering, Vol. 55, Issue 5, 2002, p. 503-518.
-
Qu S., Zhao J., Wang T. Three-dimensional stability prediction and chatter analysis in milling of thin-walled plate. The International Journal of Advanced Manufacturing Technology, Vol. 86, Issues 5-8, 2016, p. 2291-2300.
-
Wan M., et al. A unified stability prediction method for milling process with multiple delays. International Journal of Machine Tools and Manufacture, Vol. 50, Issue 1, 2010, p. 29-41.
-
Kersting P., Biermann D. Modeling techniques for simulating workpiece deflections in NC milling. CIRP Journal of Manufacturing Science and Technology, Vol. 7, Issue 1, 2014, p. 48-54.
-
Kiselev I., Voronov S. A., Arshinov S. Multi-variant simulation of milling of 3-d shaped detail considering changing of workpiece rigidity while cutting. ASME International Design Engineering Technical Conferences, 2014.
-
Voronov S. A., Kiselev I. A., Yakovlev M. G. Identification of the cutting force coefficients via milling process simulation. Proceedings of ASME International Design Engineering Technical Conference & Computer and Information in Engineering Conference IDETC/CIE, 2012.
-
Lil J., Kilic Z. M., Altintas Y. General cutting dynamics model for five-axis ball-end milling operations. Journal of Manufacturing Science and Engineering, Vol. 142, Issue 12, 2020, p. 121003.
-
Butt M. A., et al. Five-axis milling vibration attenuation of freeform thin-walled part by eddy current damping. Precision Engineering, Vol. 51, 2018, p. 682-690.
-
Gubanov G. Broadband pneumatic mass damper for the elimination of workpiece vibrations. CIRP Journal of Manufacturing Science and Technology, Vol. 30, 2020, p. 184-194.
-
Qu S., Zhao J., Wang T. Analysis of the machining stability in milling thin-walled plate. IEEE International Conference on Robotics and Biomimetics (ROBIO), 2015, p. 1741-1745.
-
Toth M., Bachrathy D., Stepan G. Effect of wavy tool path on the stability properties of milling by the implicit subspace iteration method. The International Journal of Advanced Manufacturing Technology, Vol. 91, Issues 5-8, 2017, p. 1781-1789.
-
Insperger T., Stépán G. Stability transition between 1 and 2 degree-of-freedom models of milling. Periodica Polytechnica Mechanical Engineering, Vol. 48, Issue 1, 2004, p. 27-39.
-
Trišović N. Eigenvalue sensitivity analysis in structural dynamics. FME Transactions, Vol. 35, Issue 3, 2007, p. 149-156.
-
Kiselev I., Voronov S. A. Methodic of rational cutting conditions determination for 3-D shaped detail milling based on the process numerical simulation. ASME International Design Engineering Technical Conferences, 2014.
-
Nikolaev S., et al. Optimal milling modes identification of a jet-engine blade using time-domain technique. The International Journal of Advanced Manufacturing Technology, Vol. 107, 1983, p. 1992-2020.
-
Peigne G., Paris H., Brissaud D., Gouskov A. Impact of the cutting dynamics of small radial immersion milling operations on machined surface roughness. International Journal of Machine Tools and Manufacture, Vol. 44, Issue 11, 2004, p. 1133-1142.
