Testing of products on vibration strength and durability in the regime of chaotic oscillations

1. Introduction

The necessity for check of devices and structures on vibration strength and durability appears very often during design and development process. For example, in development of thin-walled structures and units of airplanes and ships it is necessary to test them on action of vibration spectrum peculiar to operation condition. Besides, in many branches of industry the ability of products (e.g. device, microcircuit, etc.) to perform their functions and maintain main parameters within allowable limits in vibration environment must be tested.

There is known method for vibration testing of products in the regime of harmonic vibration with continuously changeable frequency (oscillating frequency method) [1]. Method is based on cyclic increasing and decreasing of excitation frequency within the given range, and during variation of frequency the constant level of vibration is provided (vibration displacement or acceleration). Such approach makes it possible to excite sequentially different resonant regimes in testing structure. But during vibration tests it is necessary very often to realize in the structure all possible resonant regimes simultaneously in order to analyze mutual influence of different resonances. The inability to realize such tests is a substantial demerit of the method [1].

Other known method of vibration testing is based on application to the object of polyharmonic exciting force [1, 2]. This approach makes it possible to realize in testing object a complex vibration spectrum which is more consistent to real operation conditions. But practical realization of polyharmonic excitation is rather complicated (necessity for use of many vibroexciters, which generate excitation forces with different frequencies and controllable amplitudes and phases).

Some attempts were made to realize complex vibration spectrum in testing machines with nonlinear elastic supports [3, 4]. Due to nonlinear elasticity, multi-frequency vibration can be realized under the monoharmonic excitation (e.g., on super- or subharmonic resonant regimes). In this case vibration spectrum contains only harmonic components with fixed frequencies which differ from excitation frequency in an integer number of times. But very often in real conditions, products are subjected to action of vibration with continuous frequency spectrum and random amplitudes. Continuous vibration spectrum in principal cannot be realized on super- and subharmonic resonant regimes.

This paper considers the possibility to realize continuous vibration spectrum in testing machine with nonlinear elastic supports by the excitation of chaotic oscillations [5].

2. Dynamic model of vibration test bench

Vibration test bench is considered as a single-degree-of-freedom vibratory system with piecewise linear elastic characteristic (Fig. 1).

Fig. 1Dynamic model of vibration test bench

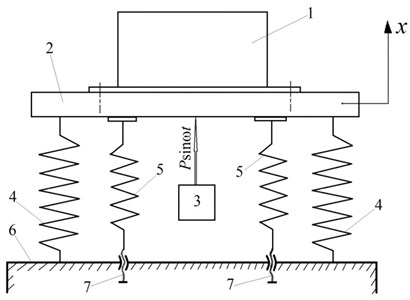
Testing object 1 is attached to working table 2, which is mounted on stationary base 6 through system of elastic supports. And elastic system is formed from main elastic supports 4 with stiffness coefficient $k_1$ and additional elastic limiters 5 with stiffness coefficient $k_2$. In static equilibrium position of the system the initial clearance between working table 2 and elastic limiters 5 is set as zero (with the aid of adjusting device 7). Therefore, bilinear elastic characteristic is realized. Working table 2 is loaded with external harmonic force $P\mathrm{s}\mathrm{i}\mathrm{n}\omega t$, which is generated by vibroexciter 3.

Assuming the origin of co-ordinate axis x in static equilibrium position of working mass $m$ on main elastic supports 4, the differential equation of forced oscillations can presented in the following form:

where $m$ is the total mass of the working table and testing object, $b$ is damping coefficient, $k_1$ is the total stiffness coefficient of the main elastic supports, $k_2$ is the total stiffness coefficient of additional elastic limiters, $P$ and $\omega$ are the amplitude and frequency of the external harmonic excitation.

By the substitution $y=k_{1}x/P$ and $\tau =t\sqrt{k_1/m}$, Eq. (1) can be transformed into the dimensionless form, more manageable for analysis:

where $\beta =b/\sqrt{k_{1}m}$ is the dimensionless damping coefficient, $\nu =\omega /{\omega }_0$ is the relative excitation frequency, ${\omega }_0=\sqrt{k_1/m}$ is free oscillations frequency of working mass $m$ on main elastic supports $k_1$.

As it is seen, solution of Eq. (2) is dependent on three dimensionless parameters $\left(\beta ,\left(k_1+k_2\right)/k_1,\nu \right)$. Analysis of solutions of Eq. (2) was made by mathematical simulation with computer program SPRING [6]. Damping factor $\beta$ was assumed constant and equal to $\beta =$ 0.1 which corresponds to the average level of losses in real vibration devices [7]. In such condition solution of Eq. (2) is dependent only on parameters $\left(k_1+k_2\right)/k_1$ and $\nu$.

3. Realization of chaotic oscillatory regimes in vibration test bench

In accordance with research results, chaotic oscillations can be excited in the system under study only within the limited space of parameters $\stackrel{-}{k}=\left(k_1+k_2\right)/k_1$ and $\nu$. Fig. 2 shows the domain of existence of chaotic oscillations on the coordinate plane $\stackrel{-}{k}$ and $\nu$. Within this domain chaotic oscillations are realized under the any possible initial conditions, i.e. chaotic attractors become the globally stable [5]. Therefore, in order to realize the chaotic oscillatory regimes in vibration test bench, it is necessary to tune the system on this domain (for example, by the variation of parameters $\stackrel{-}{k}$ and $\nu$).

Fig. 2The domain of existence of chaotic oscillations

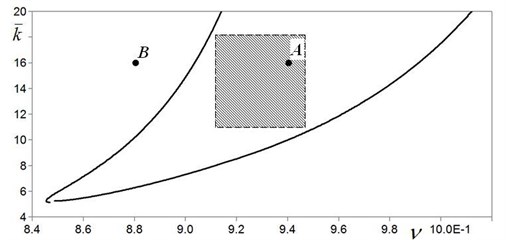
But during operation of vibration test bench, some relatively small and non-predicted changes of parameters $\stackrel{-}{k}$ and $\nu$ are possible. For example, such changes can be caused by non-predicted fluctuation of stiffness coefficients $k_1$ and $k_2$ due to stress relaxation or natural ageing of material. In such conditions operation of vibration test bench in chaotic oscillatory regime can be provided, if parameters $\stackrel{-}{k}$ and $\nu$ are taken inside the domain of existence (Fig. 2), herewith at least in small distances from the domain’s borders. Therefore, for stable realization of chaotic regime, it has been found expedient to tune the test bench on shaded part or core of the domain of existence. Mathematically the tuning of the test bench on the core part of the domain can be expressed with two conditions 11 $\le \stackrel{-}{k}\le$ 18 and 0.91 $\le \nu \le$ 0.95.

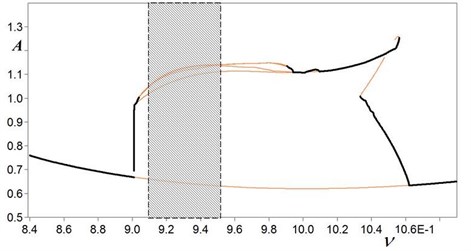
Typical bifurcation diagram for the system under study is shown in Fig. 3 on the plane of parameters $\nu$ and $A$, where $A$ is a half-swing of oscillations of the working table (the diagram is plotted assuming $\stackrel{-}{k}=$ 16 and $\beta =$ 0.1). As it is seen, in this case chaotic oscillations are realized within frequency range 0.89 $\le \nu \le$ 1.00. But to guarantee stable excitation of chaotic oscillations in vibration test bench (even in the case of non-predicted fluctuation of system’s parameters), it has been found expedient to use the more narrow frequency range 0.91 $\le \nu \le$ 0.95 (in the bifurcation diagram this recommended frequency range is section-lined).

Fig. 3Bifurcation diagram on the plane of parameters ν and A

As examples, Fig. 4 shows typical time history $y=f\left(t\right)$ of chaotic oscillations, but Fig. 5 – corresponding phase portrait on the coordinate plane “displacement $y$ – velocity $\dot{y}$”. Both graphs correspond to the point A on the domain of existence (Fig. 2, $\stackrel{-}{k}=$ 16 and $\nu =$ 0.94).

Fig. 4Typical time history y=ft of chaotic oscillations

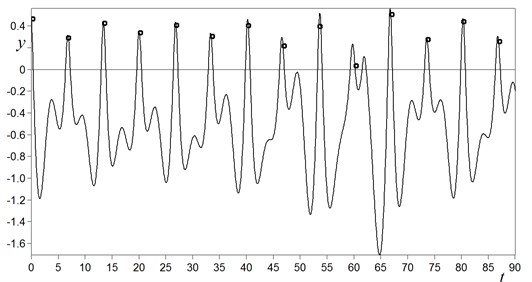
Fig. 5Typical phase portrait of chaotic oscillations

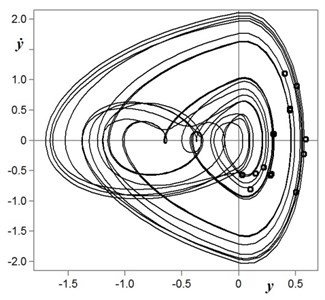
As it is seen from Fig. 4 and Fig. 5, chaotic oscillations have stochastic nature (continuous spectrum with random changes of amplitudes). Besides, this property is approved by stochastic behavior of oscillatory attractor $p$ on the phase plane “co-ordinate $y_p$ – velocity ${\dot{y}}_p$” (Fig. 6).

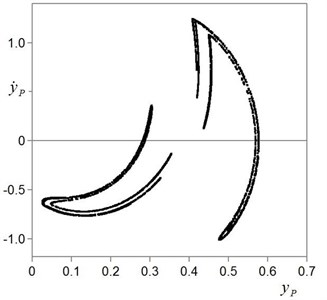
Fig. 6Chaotic attractor on the phase plane “co-ordinate yp – velocity y˙p” (for the case k-= 16, β= 0.1 and ν= 0.94)

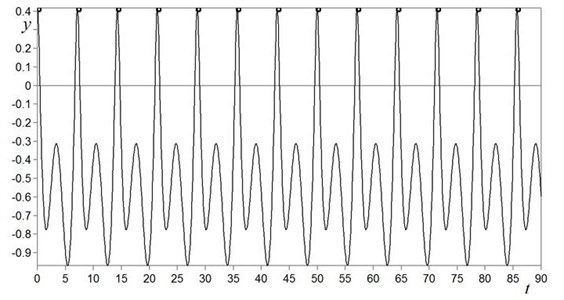
Outside of the domain of existence of chaotic oscillations (Fig. 2), stationary periodic regimes with discrete frequency spectrum are realized. As an example, Fig. 7 shows the time history $y=f\left(t\right)$ of the stationary periodic regime which is realized in the case of $\stackrel{-}{k}=$ 16 and $\nu =$ 0.88 (point B on the domain of existence, see Fig. 2).

As it is seen from Fig. 7, in the outside of the domain of existence oscillations don’t have stochastic nature. This example confirms that conditions 11 $\le \stackrel{-}{k}\le$ 18 and 0.91 $\le \nu \le$ 0.95 are necessary for the realization in vibration test bench of chaotic oscillations.

Fig. 7Time history y=ft of the stationary periodic regime which is realized in the outside of the domain of existence of chaotic oscillations (k-= 16, β= 0.1 and ν= 0.88)

4. Conclusions

In accordance with the method developed, testing of products on vibration strength and durability can be executed in the following operational procedure:

1) Testing object is attached to the working table of vibration test bench.

2) Elastic system of test bench is made from main elastic supports and additional elastic limiters. Besides, ends of main elastic supports are connected with stationary base and working table; one end of elastic limiter is attached to the stationary base, and the other one remains free.

3) In static equilibrium position of the system a clearance between free end of elastic limiter and working table is set to zero.

4) Elastic nonlinearity $\left(k_1+k_2\right)/k_1$ of the system is taken within interval 11 $\le \left(k_1+k_2\right)/k_1\le$ 18.

5) External harmonic excitation is applied to the working table. To realize chaotic oscillations, frequency $\omega$ of harmonic excitation force is taken within the range 0,91${\omega }_0\le \omega \le$0,95${\omega }_0$, where ${\omega }_0$ is a natural frequency of both working table and testing object supported on main elastic elements $k_1$.

Duration of test in the regime of chaotic oscillations is dependent on type of testing object. Chaotic oscillations are characterized with the continuous frequency spectrum and random amplitudes. Exactly such vibration is usually applied to real products and machine members in operation conditions. Therefore, realization of the proposed method will make it possible to approach the excited vibration spectrum to the operation conditions of real objects.