Abstract
In this paper, the vibration behavior features are extracted from the combination between Wavelet Transform (WT), and Finite Strip Transition Matrix (FSTM) of skew composite plates (SCPs), with variable thickness, and intermediate elastic support. Although, the results of this technique and based on the previous work done by the authors, that show the method can reflect the vibration behavior of the composite plates. Due to the method's difficulty in terms of, a lot of calculations with a large number of iterations these results may not be good choices for quick and accurate vibration behavior extracting. Thus, the new deep neural network (NN) is designed to learn and test these results carrying out by extracting vibration behavior features that reflect the important and essential information about the mode shapes in SCP. The results give high indications about the proposed technique of deep learning is a promising method, particularly when the type structures are complicated and the ambient environment is variable.
Highlights
- Extract the vibration behavior features of skew composite plates, with variable thickness, and intermediate elastic support from the combination between wavelet transform, and finite strip transition matrix.
- Design the new deep neural network to learn and test these results carrying out by extracting vibration behavior features that reflect the important and essential information about the mode shapes in skew composite plate.
- The results give high indications about the proposed technique of deep learning is a promising method, particularly when the type structures are complicated and the ambient environment is variable.
1. Introduction
The importance of to use of composite materials in many fields of technology, such as aerospace industries, marine engineering, and civil engineering is due to special features, e.g. high strength/weight ratio and corrosion resistance property, particularly under the effects of the harsh environment. Although the structures are made of these types of materials have some drawback are subject to matrix cracks, fiber breakage, and delamination. These invisible faults can lead to catastrophic structural failures [1-4].
Other major modes of failure of fiber-reinforced polymer (FRP) have a temperature, bending, tensile, stress, impact failure, and failure of the installation, etc. These types of failures are complicated and are not easy to assets, mostly when subjected to associate effects of multiple factors [5-7].
The user of an active system of structural health monitoring (SHM) to observe the safety and potential damage detection in composite plates are essential and most seriously. The function of SHM is consists of three main sub-functions, including system identification, features extraction for algorithms for detection and prediction, and reliability and risk evaluation [8-19].
The vibration behavior of composite structures is the traditional method for the intelligent detecting the defects in the composite. The mode shapes of the structure are one of the essential tools in Structural health monitoring (SHM) in the last decades, where, extracted the vibration response of composite structure for each damage type and position and analysis based on the variance in vibration parameters. In recent years, different techniques to extract the natural frequencies of composite plates have become a field of great interest in the scientific society [20-34].
To find the mode shapes for different boundary conditions with IES, numerical methods or experimental methods must be used. Some researchers have been interested in the vibration of multi-span plates using different approaches. In previous works, Altabey [35, 36] used the FSTM as one of the common use of semi-analytical approaches to extract vibration response of basalt FRP laminated variable thickness rectangular plates with IES, and he tried to improve the results accuracy and by the way, decrease the calculations efforts due to a large number of iterations by combined his method with artificial neural networks (ANNs) and response surface (RS) methods.
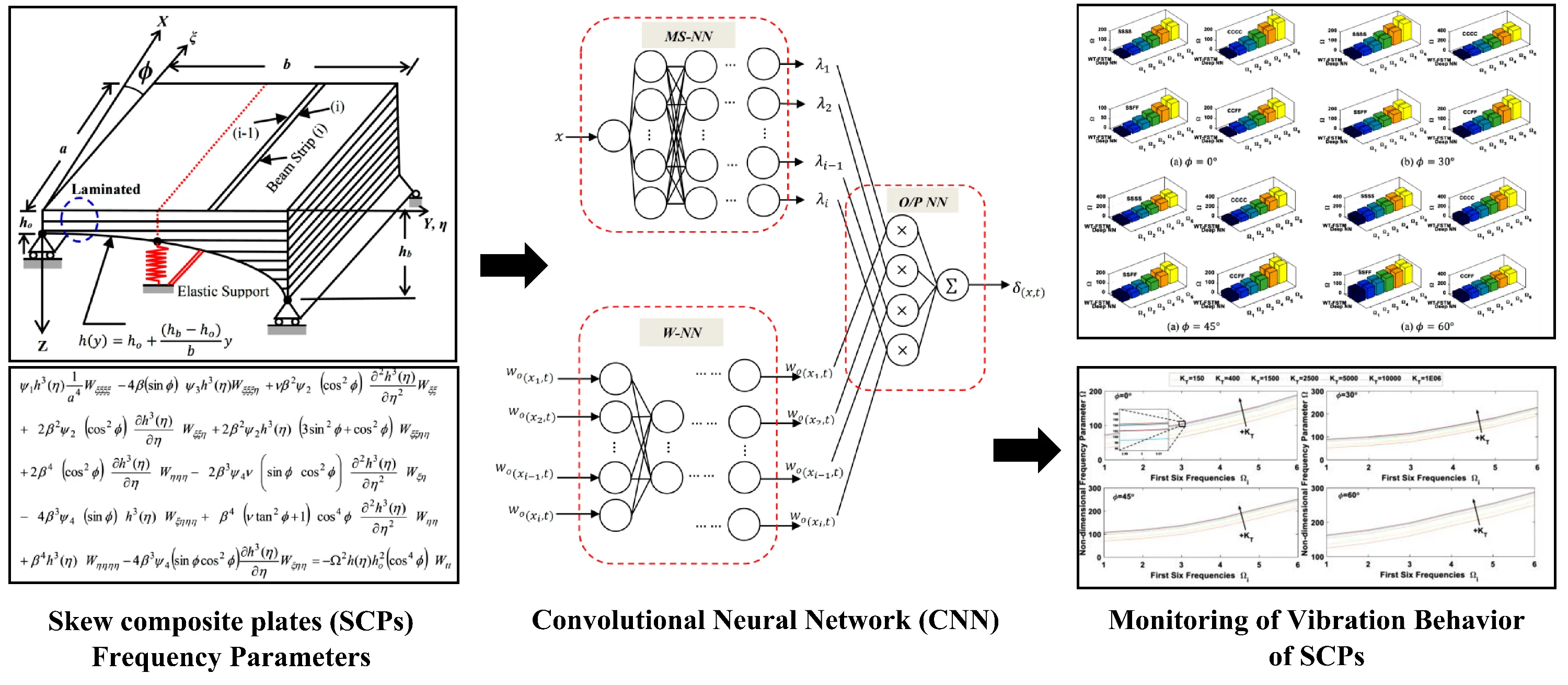
In the present research, the new deep NN is designed to predict the vibration behavior of SCPs with variable thickness and IES with a different elastic restraint coefficient () and four cases of boundary conditions (BCs) of plate edges, namely SSSS, CCCC, SSFF, and CCFF. The plate is a rectangular SCP with variable thickness function , the locations of the IES is at mid-line of the presented plate, and the plate was manufactured from basalt fiber reinforced polymer (BFRP) by using five symmetrically layers with the stacking angle [45°/–45°/45°/–45°/45°] as shown in Fig. 1. First, review the illustrated results of the utilized method by the combination of these WT and FSTM methods (WT-FSTM) to convergence the studies by checking the agreement with the results available in the literature. Second, the trained deep NN is used to predict the outcome of the extracted vibration behavior of SCPs from WT-FSTM at certain values of elastic restraint coefficients () for IES, and then it is subsequently used to predict the vibration behavior for different levels of elastic restraint coefficients () for IES. The results are predicted from the deep NN model are in very good agreement with the WT-FSTM results. Hence, the results give high indications about the proposed technique of deep learning is a promising method.
Fig. 1The geometry of rectangular SCP with variable thickness and IES
2. Model overview
The composite plate material has corresponding elastic and shear modulus values are shown in Table 1.
Table 1Model property
(GPa) | (GPa) | (GPa) | (GPa) | rho kg/m3 | ||
96.74 | 22.55 | 0.3 | 0.6 | 10.64 | 8.73 | 2700 |
The normalized partial differential equation of vibration behavior for the plates system illustrated in Fig.1 under the assumption of the classical deformation theory in terms of the plate deflection using the non-Dimensional variables and related to the skew coordinate system defined by , , and , , and after some derivation, the governing equation can be written as follows:
where , , , .
Since the treatment of IES conditions are the main objective of this paper we presented it in more detail. The line of the IES, the displacement must vanish and the normal moment must be continuous, i.e.
where: , , , , , .
3. Determination of vibration behavior using WT and FSTM
In This section, the mode shapes of the SCP will be extracted using a new method by combined between the WT and FSTM methods with an adjusting frequency parameter, in order to improve the estimated accuracy of extracting by optimized the WT entropy for adjusting frequency parameter.
3.1. Continuous wavelet transform (CWT)
Continuous wavelet transform (CWT) is a convolution process of the data sequence with a set of continuous scaled and translated versions of the mother wavelet (MW) . The translating process is a smoothing effect over the length of the data sequence to localize the wavelet in time domain , whereas the scaling process is compressing or stretching of analyzed wavelet which indicates various resolutions. The stretched wavelet is used to capture the slow changes; while the compressed wavelet is used to capture abrupt changes in the signal. The trade-off of enhancing resolution is between increased computational cost and memory by computing wavelet components and multiplying each component by the correctly dilated and translated wavelet, resulting in the constituent wavelet of the analyzed signal [37-45].
The is stretched or squeezed through varying its dilation parameter s and moved through its translation parameter (i.e. along the localized time index ):
Let be the system shape function response of FSTM, where denotes time. CWT of a function , where is the set of square-integrable functions is denoted as and defined as:
where the wavelet scale s and the period are used to adjust the frequency and time location. shows how closely correlated with . By inverse CWT, the signal can be regenerated as:
For a plate striped in the -direction by divided into discrete longitudinal strips spanning between supports as shown in Fig. 1, the free-response equation for one striped beam system may be assumed in the form:
The WT of Eq. (7) is:
The logarithm of Eq. (8) gives:
By using the straight line of the slope of the logarithm of WT modulus, we can be obtained the natural frequency of the system and it is given by:
The plot of is constant in the time domain and is equal to the natural frequency . The non-dimensional frequency parameter (NDFP) are addressed in the form:
4. Deep neural networks (NNs)
Recently, deep learning, which is a network with multiple hidden layers of neurons, has also been applied in solving and identifying the ordinary and partial differential equations [46, 47].
Deep neural networks (NNs) are one of the artificial intelligence (AI) algorithms used for solving advanced non-linear problems [48]. The networks are consist of computational nodes that connected together to create one individual network, each node is processing a calculation on input and sends the result to output connections, and maybe a node output is an input to one other node or more.
In this section, we use the outcome of the results in Section 3 of vibration behavior of SCP extracted by WT-FSTM at certain values of elastic restraint coefficients () to obtain the training data and to predict the vibration behavior for different levels of elastic restraint coefficients () not included in the results.
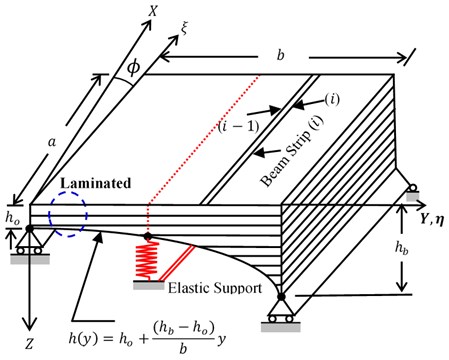
The proposed deep NN architecture connection is presented in Fig. 2. The steps of the NDFP prediction can be described through the following steps in Table 2.
Fig. 2The architecture of the proposed deep NN for the NDFP (Ω) prediction
Table 2The steps of deep NN training to predict NDFP (Ω)
NN steps | Step remark |
Data collecting | Extract the training data from the WT-FSTM of the SCP at certain values of elastic restraint coefficients () |
Training model | Divide the extracting data into three groups of data, the first one will be used for training in MS-NN for mode shapes prediction of SCP, and the second group of a dataset will be used for training in W-NN for predicting deflection , this network without hidden layers |
Testing model | The last part of the data will use to test the trained model in the training model. If the model is well-trained, the predicted results by the W-NN and MS-NN will be convergence to the real value. The training performance of suggested Deep NN is presented in Fig. 3 |
Prediction response | The response MS-NN will be used to predict the under random deflection . W-NN will be used to predict the at any location coordinate along with the SCP including the IES location presented in Section 2 |
It is important for the NN designer to check his proposed deep NN performance is suitable or not from the formula of mean square error (MSE):
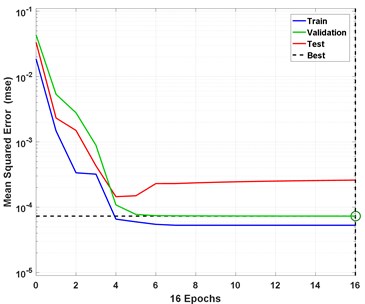
Therefore, only one global minimum for performance index based on the features of the input vectors, but the minimum local minimum of a function at finite input values, and it cannot be omitted when attaching deep NN. Therefore, we can judge on accuracy a local minimum, if it has a low closer range to global minimum and low MSE. Anyway, the designer must be selected as a suitable method to solve this problem in order to descent the local minimum with momentum. Momentum allows a network to respond not only to the local gradient but also to recent trends in the error surface. Without momentum, a network may get stuck in a shallow local minimum. Fig. 3 shows the performance curves of training with three groups for learning data.
Fig. 3Training performance of proposed NN
5. Results and discussion
In this section, after reviewing the results available in the literature, the approach of WT-FSTM are used to extract the vibration behavior of SCP with variable thickness are presented in Section 2 at certain values of elastic restraint coefficients () for IES, on the other hand, to provide the active training data to proposed deep NN, in order to extract the influence of the IES on the natural frequencies with different elastic restraint coefficients () of such plates.
5.1. Convergence study and accuracy
The importance for review of presented work results with the results available in the literature in order to validate the accuracy and reliability of the proposed technique. In this subsection, the WT-FSTM technique has been applied on a CCCC variable thickness SP with (0, 0.2, 0.4, 0.5) and (30°, 45°, 60°), and then the convergence between the results in Fig. 4 with the results from FSTM [35] will be done.
As shown in the Fig. 4, after convergence, we can see clearly generally, that the results of the presented method WT-FSTM in excellent agreement with the other accurate methods in references [23-26, 35]. On the other hand, we can see the effects of plate Skew angles (), tapered ratio () and aspect ratio ( on the NDFP () it has been increased with increasing of the , , and , in all methods WT-FSTM and the methods in the literature.
5.2. Proposed method (WT-FSTM) results
In the present study, the numerical computations using the WT-FSTM approach is applied to extract vibration behavior. Due to the method difficulty in terms of, a lot of calculations with a large number of iterations these results may not be good choices for quickly and accurate vibration behavior extracting, the new deep NN is designed to learn and test these results carrying out by extracting vibration behavior features that reflect the important and essential information about the mode shapes in SCP. The proposed method target achieved using only two different in computations of the NDFP , the first one is located at 50 the second is 750, respectively. The first six frequencies are presented in Table 3, the NDFP has been computed with different values of skew angle () at aspect ratio ( 0.5), and tapered ratio ( 0.5) to study the behavior of natural frequencies under a different skew angle for different four BCs namely SSSS, CCCC, SSFF, and CCFF.
Fig. 4Comparison of the first four natural frequencies of CCCC skew plates β= 0.5
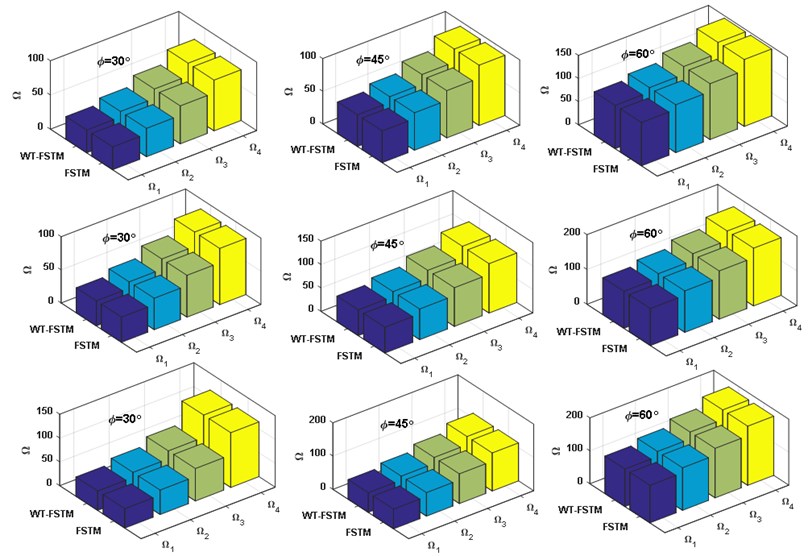
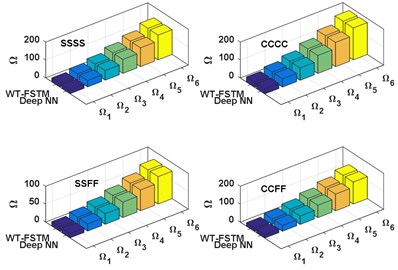
Figs. (5-6) represent the comparison between the WT-FSTM data and the deep NN predicted data NDFP for 50 and 750 respectively of four different BCs are SSSS, CCCC, SSFF, and CCFF. The results of the proposed deep NN show much satisfactory prediction quality for this case study.
Fig. 5Comparison between the WT-FSTM data and deep NN predicted data for KT= 50
a) 0°
b) 30°
c) 45°
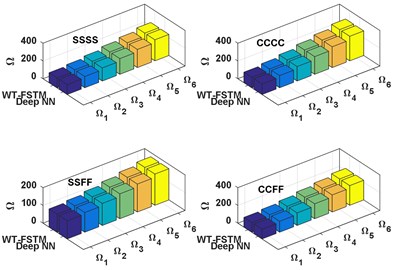
d) 60°
Fig. 6Comparison between the WT-FSTM data and deep NN predicted data for KT= 750
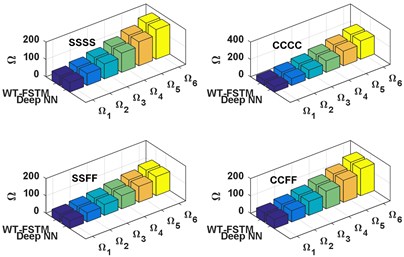
a) 0°
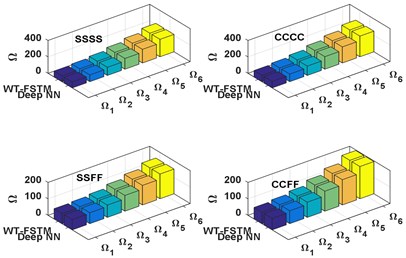
b) 30°
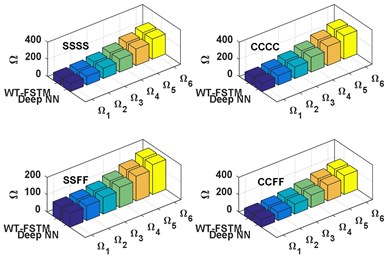
c) 45°
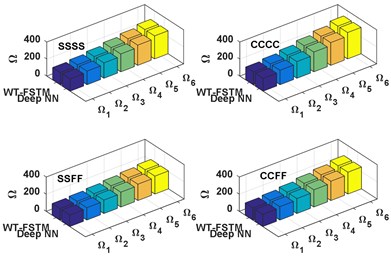
d) 60°
Table 3The first six frequencies of SCP, β= 0.5, Δ= 0.5
BCs | ||||||||
SSSS | 0° | 50 | 22.157 | 36.232 | 53.594 | 78.249 | 105.594 | 138.710 |
750 | 55.078 | 69.159 | 86.525 | 111.179 | 138.523 | 171.633 | ||
30° | 50 | 39.507 | 49.713 | 69.226 | 98.139 | 135.487 | 179.658 | |
750 | 72.428 | 82.640 | 99.1570 | 131.069 | 166.416 | 212.581 | ||
45° | 50 | 57.936 | 69.256 | 87.408 | 119.321 | 156.736 | 201.733 | |
750 | 90.857 | 102.183 | 120.339 | 152.251 | 194.665 | 234.656 | ||
60° | 50 | 112.564 | 127.407 | 148.221 | 177.583 | 204.928 | 238.044 | |
750 | 145.485 | 160.334 | 181.152 | 210.513 | 237.857 | 270.967 | ||
CCCC | 0° | 50 | 28.446 | 46.511 | 68.806 | 100.457 | 135.565 | 178.079 |
750 | 61.361 | 79.435 | 101.737 | 133.372 | 168.490 | 211.102 | ||
30° | 50 | 45.796 | 59.992 | 85.438 | 120.347 | 166.458 | 219.027 | |
750 | 78.711 | 92.916 | 114.369 | 153.262 | 196.383 | 252.050 | ||
45° | 50 | 64.225 | 79.535 | 102.620 | 141.529 | 191.707 | 241.102 | |
750 | 97.140 | 112.459 | 135.551 | 174.444 | 224.632 | 274.125 | ||
60° | 50 | 118.853 | 137.686 | 163.433 | 199.791 | 234.899 | 277.413 | |
750 | 151.768 | 170.610 | 196.364 | 232.706 | 267.824 | 310.436 | ||
SSFF | 0° | 50 | 12.286 | 20.083 | 29.716 | 43.375 | 58.538 | 76.887 |
750 | 45.206 | 53.013 | 62.639 | 76.305 | 91.465 | 109.813 | ||
30° | 50 | 31.636 | 36.564 | 48.348 | 66.265 | 90.431 | 117.835 | |
750 | 62.556 | 66.494 | 75.271 | 96.195 | 119.358 | 150.761 | ||
45° | 50 | 48.065 | 53.107 | 63.530 | 84.447 | 110.680 | 139.910 | |
750 | 80.985 | 86.037 | 96.453 | 117.377 | 143.607 | 172.836 | ||
60° | 50 | 102.693 | 111.258 | 124.343 | 140.709 | 157.872 | 176.221 | |
750 | 135.613 | 144.188 | 157.266 | 173.639 | 190.799 | 209.147 | ||
CCFF | 0° | 50 | 19.603 | 32.054 | 47.423 | 69.228 | 93.425 | 122.724 |
750 | 52.529 | 64.981 | 80.346 | 102.154 | 126.355 | 155.641 | ||
30° | 50 | 36.953 | 47.535 | 64.055 | 91.118 | 126.318 | 163.672 | |
750 | 69.879 | 78.462 | 92.978 | 122.044 | 154.248 | 196.589 | ||
45° | 50 | 55.382 | 65.078 | 81.237 | 110.300 | 149.567 | 185.747 | |
750 | 88.308 | 98.005 | 114.160 | 143.226 | 182.497 | 218.664 | ||
60° | 50 | 110.010 | 123.229 | 142.050 | 168.562 | 192.759 | 222.058 | |
750 | 142.936 | 156.156 | 174.973 | 201.488 | 225.689 | 254.975 |
5.3. Deep NN performance
The performances of suggested deep NN are presented in Table 4 and Fig. 3, the MSE and accuracy of predicted data are calculated from Eq. 12 for NDFP . From Table 4 and Fig. 3 the value of MSE and accuracy of training data are 7.2 E-5 and 99.7 % respectively and validating data are 6.2 E-5 and 99.8 % respectively. From NN performance shows in Table 4 and Fig. 3, the proposed deep NN gave a good prediction for vibration behavior data in the presented SCP.
Table 4Mean square error (MSE) and accuracy values
Data | MSE | Accuracy |
Training | 7.2 E-5 | 99.7 % |
Validating | 6.2 E-5 | 99.8 % |
5.4. Deep NN predicting results
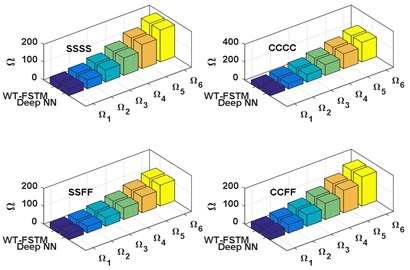
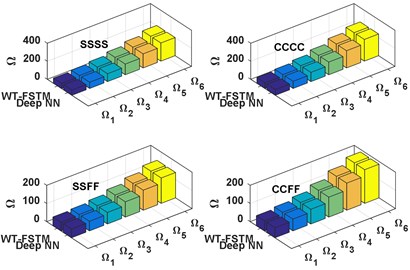
In this subsection, the main target of design the deep NN of predicting the vibration behavior data of SCP under different elastic restraint coefficients () is achieved, chosen 7 different for different four BCs (SSSS, CCCC, SSFF, and CCFF). The deep NN predicted results of the first six frequencies of SCP with 0.5 and 0.5 are shows in Fig. 7.
Moreover, the influence of the IES on the vibration behavior of the SCPs with variable thickness is shown in Fig. 7. As shown in the Fig. 7 for all values of skew angle () and all types of BCs, the first six frequencies are increasing with increasing of the value of elastic restraint coefficient (). whereas the frequencies rapidly increase with for small values of elastic restraint coefficient (), and the influence of IES becomes negligible at high values. On the other hand for all values of skew angle (), the first six frequencies for fully clamped (CCCC) plate are the highest frequencies, and the semi-simply supported (SSFF) plate is the lowest one, while, the other two boundaries (SSSS and CCFF) were rested between them. also, we can see the effects of plate skew angles () on the NDFP () it has been increased with increasing of the. skew angles.
Fig. 7The deep NN predicted results of NDFP (Ω)
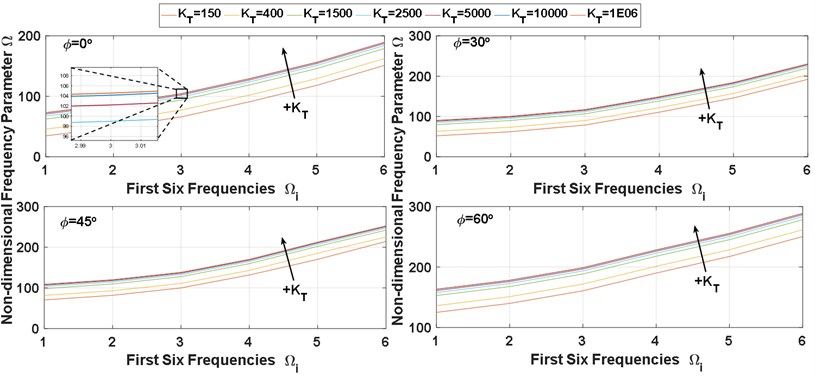
a) SSSS
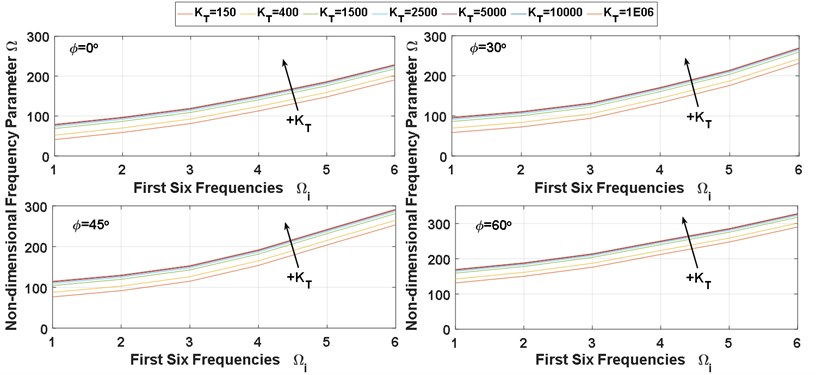
b) CCCC
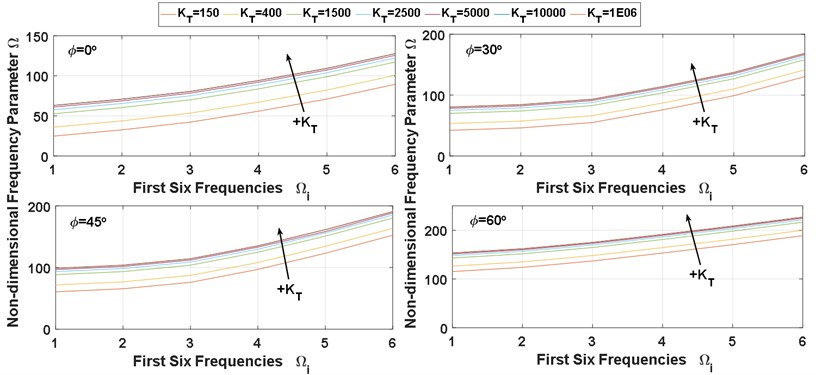
c) SSFF
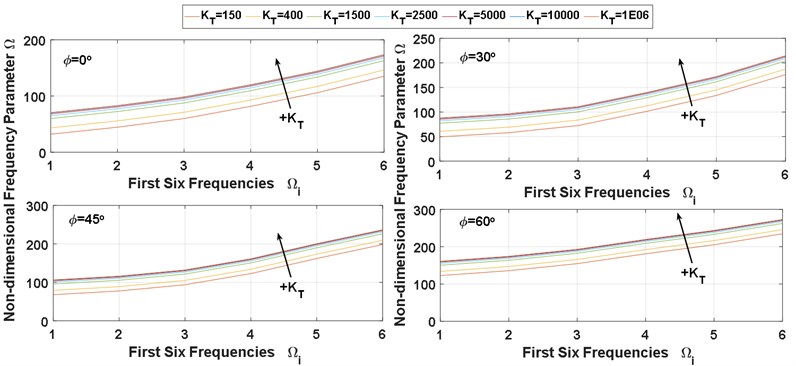
d) CCFF
6. Conclusions
By a combination of the WT and FSTM method (WT-FSTM) was used to extract the vibration behavior of SCP with variable thickness, and IES, the plate is made from BFRP laminated. First, To investigate from accuracy and reliability of the proposed technique, the convergence between the proposed study results with the results available in the literature has been checked, thus validating the accuracy and reliability of the proposed technique. Then, due to the proposed method's difficulty in terms of, a lot of calculations with a large number of iterations, these results may not be good choices for quick and accurate vibration behavior extracting. Thus, the new deep neural network (NN) is designed to learn and test these results carrying out by extracting vibration behavior features that reflect the important and essential information about the mode shapes in SCP. The influence of , , , and on the predicted NDFP of the plate, has been studied, with four different support conditions (SSSS, CCCC, SSFF, and CCFF).
Based on the WT-FSTM and the deep NN predicted results, we conclude that the deep NN predicted results of NDFP () are in very good agreement with the proposed method results WT-FSTM with an accuracy of training and validating data are 99.7 % and 99.8 % respectively.
References
-
Zhao Y., Noori M., Altabey W. A., Ghiasi R., Wu Z. A fatigue damage model for FRP composite laminate systems based on stiffness reduction. Structural Durability and Health Monitoring, Vol. 13, Issue 1, 2019, p. 85-103.
-
Zhao Y., Noori M., Altabey W. A., Naiwei L. Reliability evaluation of a laminate composite plate under distributed pressure using a hybrid response surface method. International Journal of Reliability, Quality and Safety Engineering, Vol. 24, Issue 3, 2017, p. 1750013.
-
Altabey W. A., Noori M. Fatigue life prediction for carbon fibre/epoxy laminate composites under spectrum loading using two different neural network architectures. International Journal of Sustainable Materials and Structural Systems (IJSMSS), Vol. 3, Issue 1, 2017, p. 53-78.
-
Wang T., Noori M., Altabey W. A. Identification of cracks in an Euler-Bernoulli beam using bayesian inference and closed-form solution of vibration modes. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 2020, https://doi.org/10.1177/1464420720969719.
-
Altabey W. A. An exact solution for mechanical behavior of BFRP Nano-thin films embedded in NEMS. Advances in Nano Research, Vol. 5, Issue 4, 2017, p. 337-357.
-
Altabey W. A. A study on thermo-mechanical behavior of MCD through bulge test analysis. Advances in Computational Design, Vol. 2, Issue 2, 2017, p. 107-119.
-
Ghannadi P., Kourehli S. S., Noori M., Altabey W. A. Efficiency of grey wolf optimization algorithm for damage detection of skeletal structures via expanded mode shapes. Advances in Structural Engineering, Vol. 23, Issue 13, 2020, p. 2850-2865.
-
Ghiasi R., Ghasemi M. R., Noori M., Altabey W. A. A non-parametric approach toward structural health monitoring for processing big data collected from the sensor network. Structural Health Monitoring, 2019.
-
Altabey W. A. Detecting and predicting the crude oil type inside composite pipes using ECS and ANN. Structural Monitoring and Maintenance, Vol. 3, Issue 4, 2016, p. 377-393.
-
Altabey W. A. FE and ANN model of ECS to simulate the pipelines suffer from internal corrosion. Structural Monitoring and Maintenance, Vol. 3, Issue 3, 2016, p. 297-314.
-
Altabey W. A., Noori M. Detection of fatigue crack in basalt FRP laminate composite pipe using electrical potential change method. Journal of Physics: Conference Series, Vol. 842, 2017, p. 012079.
-
Zhao Y., Noori M., Altabey W. A., Zhishen W. Fatigue damage identification for composite pipeline systems using electrical capacitance sensors. Smart Materials and Structures, Vol. 27, Issue 8, 2018, p. 085023.
-
Altabey W. A. Delamination evaluation on basalt FRP composite pipe by electrical potential change. Advances in Aircraft and Spacecraft Science, Vol. 4, Issue 5, 2017, p. 515-28.
-
Altabey W. A. EPC method for delamination assessment of basalt FRP pipe: electrodes number effect. Structural Monitoring and Maintenance, Vol. 4, Issue 1, 2017, p. 69-84.
-
Altabey W. A., Noori M., Alarjani A., Zhao Y. Nano-delamination monitoring of BFRP nano-pipes of electrical potential change with ANNs. Advances in Nano Research, Vol. 9, Issue 1, 2020, p. 1-13.
-
Altabey W. A., Noori M., Alarjani A., Zhao Y. Tensile creep monitoring of basalt fiber-reinforced polymer plates via electrical potential change and artificial neural network. Scientia Iranica, Transactions on Mechanical Engineering (B), Vol. 27, Issue 4, 2020, p. 1995-2008.
-
Altabey W. A. The thermal effect on electrical capacitance sensor for two-phase flow monitoring. Structural Monitoring and Maintenance, Vol. 3, Issue 4, 2016, p. 335-347.
-
Altabey W. A. An exact solution for acoustic simulation based transmission loss optimization of double-chamber silencer. Journal of Sound and Vibration (SV), Vol. 54, Issue 4, 2020, p. 215-224.
-
Ghiasi R., Noori M., Altabey W. A., Silik A., Wang T., Zhishen W. Uncertainty handling in structural damage detection via non-probabilistic meta-models and interval mathematics, a data-analytics approach. Applied Sciences, Vol. 11, Issue 2, 2021, p. 770, https://doi.org/10.3390/app11020770.
-
Laura P. A. A., Grossi R. O., Soni S. R. Free vibrations of a rectangular plate of variable thickness elastically restrained against rotation along three edges and free on the forth edge. Journal of Sound and Vibration, Vol. 62, 1979, p. 493-503.
-
Mukhopadhyay M. Free vibration of rectangular plates with edges having different degrees of rotational restraint. Journal of Sound and Vibration, Vol. 67, Issue 4, 1979, p. 459-468.
-
Malhotra S. K., Ganesan N., Veluswami M. A. Vibration of orthotropic square plate having variable thickness (Parabolic Shape). Journal of Sound and Vibration, Vol. 119, 1987, p. 184-188.
-
Dokainish M. A., Kumar K. Vibration of orthotropic parallaogramic plates with variable thickness, AIAA Journal, Vol. 11, 1973, p. 1618-1621.
-
Bardell N. S. The free vibration of skew plates using the hierarchical finite element method. Journal of Computers and Structures, Vol. 45, 1992, p. 841-874.
-
Singh B., Saxcna V. Transverse vibration of skew plate with variable thickness. Journal of Sound and Vibration, Vol. 206, 1997, p. 1-13.
-
Mizusawa T., Kajita T., Naruoka M. Vibration of skew plates by using B-Spline functions. Journal of Sound and Vibration, Vol. 62, 1979, p. 301-308.
-
Chopra I., Durvasula S. Natural frequencies and modes of tapered skew plates. International Journal of Mechanical Sciences, Vol. 13, 1971, p. 935-944.
-
Liu W. H., Chang I. B. Vibration of non-uniform skewed cantilever plats by the method of finite element transfer matrix. Journal of Sound and Vibration, Vol. 136, 1990, p. 157-163.
-
Garg A. K., Khare R. K., Kant T. Free vibration of skew fiber reinforced composite and sandwich laminates using a shear deformable finite element model. Journal of Sandwich Structures and Materials, Vol. 8, 2006, p. 33-52.
-
Li Z., Noori M., Altabey W. A. An experimental study on the seismic performance of adobe walls. Structural Durability and Health Monitoring, 2020, (in press).
-
Zhao Y., Noori M., Altabey W. A. Reaching law based sliding mode control for a frame structure under seismic load. Journal of Earthquake Engineering and Engineering Vibration, Vol. 20, Issue 1, 2021, p. 25-37, https://doi.org/10.1007/s11803-021-2003-1.
-
Narjabadifam P., Hoseinpour R., Noori M., Altabey W. Practical seismic resilience evaluation and crisis management planning through GIS-based vulnerability assessment of buildings. Journal of Earthquake Engineering and Engineering Vibration, Vol. 20, Issue 2, 2021, p. 25-37, https://doi.org/10.1007/s11803-021-2003-1.
-
Setoodeh A. R., Karami G. A. A solution for the vibration and buckling of composite laminates with elastically restrained edges. Journal of Computers and Structures, Vol. 60, 2003, p. 245-253.
-
Cheung Y. K., Zhou D. Vibration analysis of Symmetrically Laminated rectangular plates with intermediate line supports. Journal of Computer and Structures, Vol. 79, 2001, p. 33-41.
-
Al-Tabey W. A. Vibration Analysis of Laminated Composite Variable Thickness Plate Using Finite Strip Transition Matrix Technique and MATLAB Verifications. Chapter 21, InTech, 2014, p. 283-620.
-
Altabey W. A. Prediction of natural frequency of basalt fiber reinforced polymer (FRP) laminated variable thickness plates with intermediate elastic support using artificial neural networks (ANNs) method. Journal of Vibroengineering, Vol. 19, Issue 5, 2017, p. 3668-3678.
-
Noori M., Haifegn W., Altabey W. A., Ahmad I. H. S. A modified wavelet energy rate based damage identification method for steel bridges. Scientia Iranica, International Journal of Science and Technology, Transactions on Mechanical Engineering (B), Vol. 25, Issue 6, 2018, p. 3210-3230.
-
Zhao Y., Noori M., Altabey W. A., Seyed B. B. Mode shape based damage identification for a reinforced concrete beam using wavelet coefficient differences and multi-resolution analysis. Journal of Structural Control and Health Monitoring, Vol. 25, Issue 3, 2017, p. e2041.
-
Zhao Y., Noori M., Altabey W. A. Damage detection for a beam under transient excitation via three different algorithms. Journal of Structural Engineering and Mechanics, Vol. 63, Issue 6, 2017, p. 803-817.
-
Zhao Y., Noori M., Altabey W. A., Awad T. A Comparison of three different methods for the identification of hysterically degrading structures using BWBN model. Journal of Frontiers in Built Environment, 2019, Vol. 4, p. 80.
-
Silik A., Noori M., Altabey W. A., Ghiasi R. Comparative analysis of wavelet transform for time-frequency analysis and transient localization in structural health monitoring. Journal of Structural Durability and Health Monitoring, 2020, (in press).
-
Silik A., Noori M., Altabey W. A. Ghiasi R. Choosing optimum levels of wavelet multi-resolution analysis for time-varying signals in structural health monitoring. Journal of Structural Control and Health Monitoring, 2020, (in press).
-
Ashory M. R., Khatibi M. M., Jafari M., Malekjafarian A. Determination of mode shapes using wavelet transform of free vibration data. Journal of Archive of Applied Mechanics, Vol. 83, 2013, p. 907-921.
-
Miranda F. J. Wavelet analysis of lightning return stroke. Journal of Atmospheric and Solar-Terrestrial Physics, Vol. 70, Issues 11-12, 2008, p. 1401-1407.
-
Kumar R., Ismail M., Zhao W., Noori M., Yadav A. R., Chen S., Singh V., Altabey W. A., Silik A. I. H., Kumar G., Kumar J., Balodi A. Damage detection of wind turbine system based on signal processing approach: a critical review. Journal of Clean Technologies and Environmental Policy, 2021, https://doi.org/10.1007/s10098-020-02003-w.
-
Wang T., Altabey W. A., Noori M., Ghiasi R. A deep learning based approach for response prediction of beam-like structures. Structural Durability and Health Monitoring, Vol. 14, Issue 4, 2020, p. 315-338.
-
Kost A., Altabey W. A., Noori M., Awad T. Applying neural networks for tire pressure monitoring systems. Structural Durability and Health Monitoring, Vol. 13, Issue 3, 2019, p. 247-266.
-
Zhao Y., Noori M., Altabey W. A., Ghiasi R., Wu Z. Deep learning-based damage, load and support identification for a composite pipeline by extracting modal macro strains from dynamic excitations. Journal of Applied Sciences, 2018, Vol. 8, Issue 12, p. 2564.
