Effect of mistuning parameters on dynamic characteristics of mistuned bladed disk

1. Introduction

Tenon and mortise structure has the advantages of large load-bearing, small structure size and convenient maintenance and replacement. Therefore, tenon and mortise structure is widely used in aero-engine compressor and other power mechanical bladed disk system. However, due to the complexity of the working environment, the tenon and mortise structure of bladed disk system is prone to failure, The nonlinear factors such as gap and friction between tenon and mortise make the vibration characteristics of bladed disk system more complex, especially for mistuned bladed disk system.

Many scholars have carried out a lot of research on the non-linear factors of mortise and tenon. Cha [1] proposed an analysis method based on the equivalent linearization method to calculate the statistical characteristics of the nonlinear response, and studied the relationship between the vibration mode of the system and the performance of the friction damper. Sinclair [2-4] found that the non-linearity of the tenon system is caused by the friction caused by the deformation of the tenon. Petrov [5] developed an effective method to analyze the forced response of nonlinear periodic symmetric structures, and used this method to analyze the tuned bladed disk system with friction damping and gap. Ender [6] used the lumped mass model to calculate the effect of different dry friction on the vibration of bladed disk system. Wang [7] established a mass spring model with dry friction by harmonic balance method, taking into account the effects of coupling strength, viscosity damping ratio, excitation force amplitude to friction amplitude ratio, and the degree of dry friction disharmony on the bladed disk response. Wang [8] established a practical model of bladed disk system, which considered the random mistuning of the delayed dry friction damping, and analyzed the effect of dry friction on the vibration localization of the random mistuning bladed disk system by the incremental harmonic balance method. The results show that the nonlinear friction damping also leads to the localized phenomenon of the tuned disk. Firrone [9] proposes an overlapping method, which combines the static and dynamic displacements of blade disk and damper to calculate the forced response of blade disk system. Zhang [10] used the micro sliding model of friction damper to study the blade root dry friction, and found that the blade root dry friction can effectively reduce the vibration amplitude of mistuned blade disk system. Ma [11] established a finite element model of tenon joint structure by using 1/38 model, and comprehensively considered the effects of centrifugal force, friction coefficient, installation angle and contact area on the contact characteristics of tenon and mortise. The results show that the friction coefficient can effectively affect the maximum contact pressure and sliding distance, but the installation angle of tenon has no obvious effect on the maximum sliding distance. Peng [12], Wang [13] and Chen [14] considered the influence of different fit gap on the stress distribution of tenon and mortise. Zeng [15] established a nonlinear dynamic model of tenon and mortise with dry friction and gap by using a lumped parameter model, and analyzed the vibration response of mistuned bladed disk system by using numerical method. It was found that mistuned bladed disk system would lead to complex nonlinear dynamic behavior. Liu [16] used the anti-aliasing time-frequency fusion algorithm and considered the three-dimensional micro sliding friction contact, established the non-linear dry friction damping mistuned bladed disk system model with 18 blades in the form of density mistuned, and analyzed the influence of the positive pressure on the contact surface and the double mistuned blade mass on the vibration characteristics of the bladed disk system. The results show that the nonlinear friction damping can effectively suppress the vibration of the mistuned bladed disk system. Santosh [17] proposed a new damping method applied to the rotating condition of wind turbine blades. In this method, containers filled with spherical particles are alternately installed at four different positions on each blade. Experiments were carried out at different speeds and different positions of the container, and different damping effects were obtained, and the best installation position of the shock absorber was found. Zhao [18] based on the bladed disk model, they used intelligent optimization algorithm to optimize the vibration reduction of bladed disk system. Mashayekhi [19] proposed an efficient model order reduction technique for forced vibration analysis of a mistuned bladed disk with friction contact. Afzal [20] investigated the damping potential of multiple friction contacts in a bladed disk. Friction contacts at tip shrouds and strip dampers are considered. It is shown that friction damping effectiveness can be potentially increased by using multiple friction contact interfaces. Yang [21] established a fast prediction method for forced vibration response of bladed disks with contact interfaces. Coulomb friction model is used to simulate the contact state between tenon and mortise.

In this paper, a lumped parameter model of the mistuned blade disk system including blade, tenon and disk is established for the compressor blade disk system of the aeroengine. The effect of the coupling stiffness, gap and friction of the tenon on the vibration characteristics of the mistuned blade disk system is considered. Blade damping mistuning and tenon damping mistuning on the vibration characteristics of the mistuned bladed disk under strong coupling and weak coupling are discussed respectively.

2. Dynamic model of the bladed disk system

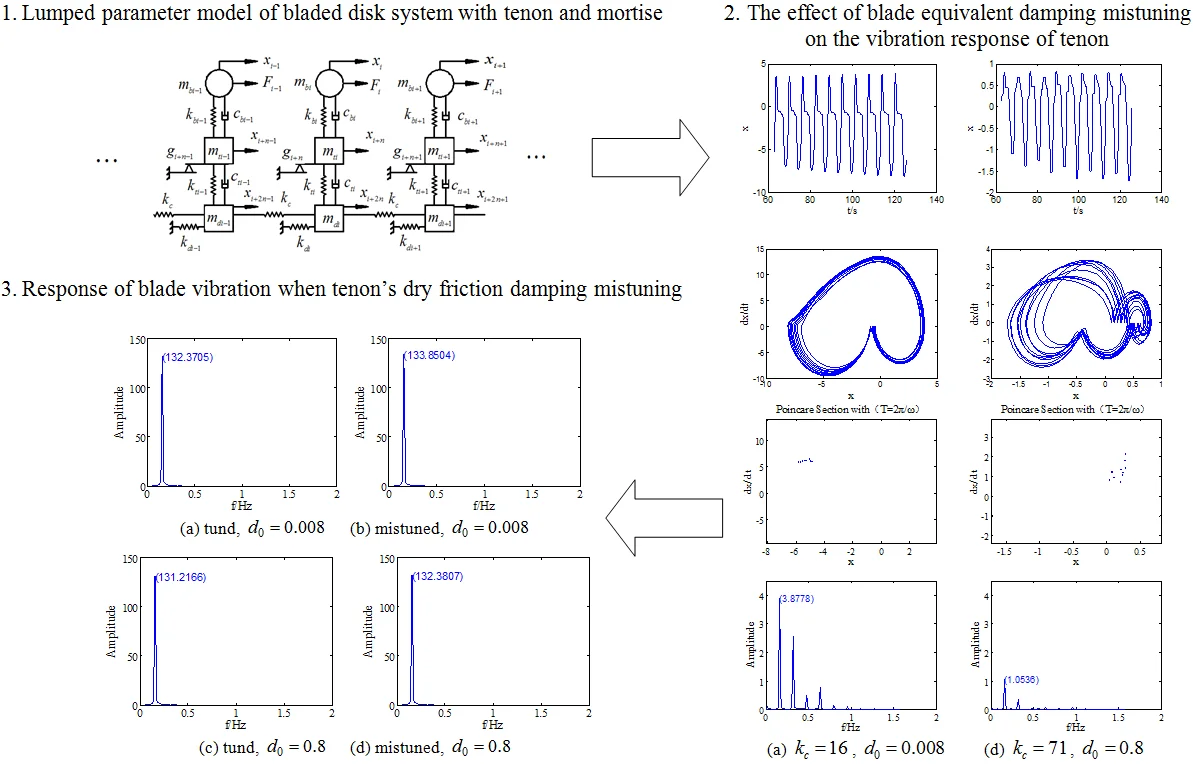
The compressor bladed disk system of aero-engine is connected by blade and disk through tenon and mortise structure. The blade is installed on the disk through tenon. The tenon stiffness and damping are simplified as the lumped parameter dynamic model of the blade disk system with equivalent stiffness and damping, as shown in Fig. 1. Set the number of sectors to $n$, $m_{bi}$, $m_{ti}$ and $m_{di}$ are the equivalent mass of blade body, blade tenon and wheel disk of the $i$th sector represently, $k_{bi}$, $k_{ti}$ and $k_{di}$ are the equivalent stiffness of blade body, tenon and disk of the $i$th sector represents, $c_{bi}$ and $c_{ti}$ are the equivalent damping of blade body and blade tenon of the ith sector, $F_i$ is the exciting force acting on the $i$th sector, $k_c$ is the coupling stiffness between sectors. Set $m_{bi}$, $m_{ti}$ and $m_{di}$ displacements are $x_i$, $x_{i+n}$, $x_{i+2n}$.

When there is a small gap between tenon and mortise, the coupling effect of blade vibration in adjacent sector is variable. Set the initial gap of mortise is $d_0$, the coupling force between disks can be simplified as the elastic force of Eq. (1):

If the tenon of the $i$th sector bears the force from the sectors on the left and right sides respectively are $f_L$ and $f_R$:

Fig. 1Lumped parameter model of bladed disk system with tenon and mortise

The friction between the blade tenon and the disk mortise adopts the Coulomb friction model shown in Eq. (4):

where, $\mu$ is the coefficient of friction; $N_{i+n}$ is normal pressure; $\mathrm{s}\mathrm{g}\mathrm{n}$ is a symbolic function, when relative sliding speed ${\dot{x}}_{i+n}$ greater than zero, equal to zero and less than zero respectively, $\mathrm{s}\mathrm{g}\mathrm{n}$return values are 1, 0, and –1, respectively.

The exciting force of air flow acting on the $i$th blade is:

where $F_{}^0$ is the amplitude of the exciting force on the $i$th rotor blade, $\omega$ is the excitation frequency, $n$ is the number of rotor blades, ${\varphi }_i$ represents the phase angle of the traveling wave excitation force on the $i$th blade, as shown in Eq. (6):

where is the order of excitation.

The dynamic differential equation of the $i$th sector of the bladed disk system is obtained by analyzing the force on the $i$th sector:

Then:

The dynamic equation of the whole disk system is:

where the displacement vector is $\left\{X\right\}={\left\{x_1,\cdots ,x_i,\cdots ,x_{i+n},\cdots ,x_{i+2n},\cdots ,x_{3n}\right\}}_{3n\times 1}^T$.

The force vector is $\left\{F\right\}={\left\{F_1,F_1,\cdots ,F_n,g_{1+n},g_{2+n},\cdots ,g_{2n},2k_c{d}_0,\cdots ,2k_c{d}_0\right\}}_{3n\times 1}^T$.

The mass matrix is:

where:

The damping matrix is:

where:

The stiffness matrix is:

where:

The dimensionless parameters of disk system are defined as follows: blade body equivalent mass $m_b=\text{1}$, blade tenon equivalent mass $m_t=\text{3.75}$, equivalent mass of wheel disk $m_d=\text{3}$, blade equivalent stiffness $k_b=\text{1}$, equivalent stiffness of tenon $k_t=\text{9.1}$, equivalent stiffness of disk $k_d=\text{1.1}$, select coupling stiffness $k_c=\text{16}$ is weak coupling, coupling stiffness $k_c=\text{71}$ is strong coupling, blade equivalent damping $c_b=\text{0.05}$, equivalent damping of tenon$c_t=\text{0.625}$, order of exciting force $E=\text{6}$. In order to verify the accuracy of the calculation model in this paper, Using the above parameters, through comparison with the model in reference [8], the comparison results are shown in Fig. 2. The horizontal and vertical coordinates are dimensionless physical quantities without units.

Fig. 2Model validation

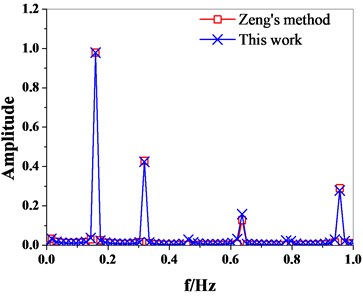
It can be seen from Fig. 2 that the model in this paper is in good consistent with the model in reference [15], which verifies the correctness of the model in this paper.

3. Nonlinear dynamic analysis of the Tenon and mortise of mistuned bladed disk

3.1. Nonlinear vibration characteristics of tenon with dry friction

The dynamic equation of the tuned bladed disk is:

13

$\left[M\right]\left\{\ddot{X}\right\}+\left[C\right]\left\{\dot{X}\right\}+\left[K\right]\left\{X\right\}=\left\{F\right\}.$

When mass, damping and stiffness are mistuning, the dynamic equation of the mistuned bladed disk is:

14

$\left[M+\mathrm{\Delta }M\right]\left\{\ddot{X}\right\}+\left[C+\mathrm{\Delta }C\right]\left\{\dot{X}\right\}+\left[K+\mathrm{\Delta }K\right]\left\{X\right\}=\left\{F\right\},$

where, $M$, $C$ and $K$ are mass matrix, damping matrix and stiffness matrix respectively. $\mathrm{\Delta }M$ is the mass mistuning matrix, $\mathrm{\Delta }C$ is the damping mistuning matrix, $\mathrm{\Delta }K$ is the stiffness mistuning matrix:

15

$\left[\mathrm{\Delta }M\right]={\left[\begin{array}{llll}\mathrm{\Delta }{m}_{b1}& & & \\ & \mathrm{\Delta }{m}_{b2}& & \\ & & \ddots & \\ & & & \mathrm{\Delta }{m}_{bn}\end{array}\right]}_{n\times n},$

16

$\left[\mathrm{\Delta }C\right]={\left[\begin{array}{llll}\mathrm{\Delta }{c}_{b1}& & & \\ & \mathrm{\Delta }{c}_{b2}& & \\ & & \ddots & \\ & & & \mathrm{\Delta }{c}_{bn}\end{array}\right]}_{n\times n},$

17

$\left[\mathrm{\Delta }{K}_b\right]={\left[\begin{array}{llll}\mathrm{\Delta }{k}_{b1}& & & \\ & \mathrm{\Delta }{k}_{b2}& & \\ & & \ddots & \\ & & & \mathrm{\Delta }{k}_{bn}\end{array}\right]}_{n\times n},$

where, $\mathrm{\Delta }{m}_{bi}$, $\mathrm{\Delta }{c}_{bi}$ and $\mathrm{\Delta }{k}_{bi}$ are mass mistuning, damping mistuning and stiffness mistuning of the ith blade respectively.

In this paper, the dynamic analysis of the mistuned bladed disk is carried out when only the blade stiffness mistuning is considered, and the tenon and mortise gap and friction are considered.

3.1.1. Vibration response of tenon without friction between Tenon and mortise

Considering that the coupling stiffness between the disks is strong coupling and weak coupling, the excitation frequency $\omega =\text{1}$ is selected, and the initial gap $d_0=\text{0.008}$ and $d_0=\text{0.8}$ are respectively. Fig. 3 shows the vibration response of tenon without friction.

When friction is not taken into account, 2-9 SHG appears in the response spectrum of the strong coupling small gap system, and the 2, 4, 7 SHG components are larger. When the coupling stiffness is weak coupling and small gap, the maximum amplitude is 4.165, and there are multiple frequency doubling phenomena in the system response spectrum, among which the second harmonic component is the largest. There are irregular points in the section of the tenon Poincare, and the waveform in time domain is random. When the coupling stiffness is strong coupling and large gap, the maximum amplitude is 1.041, and the system response spectrum appears 2-9 frequency doubling, among which 2, 4, 7 frequency components are larger. There are irregular points in the Poincare section of the tenon, and the position of the unsmooth waveform in time domain may be caused by the influence of frequency components of 2, 4 and 7. When the coupling stiffness is weak coupling and large gap, the maximum amplitude is 4.3453. There are multiple frequency doubling phenomena in the system response spectrum, among which the second frequency component is the largest. There are irregular points in the tongued Poincare section, and the time-domain waveform is random. These characteristics indicate that the system is in a chaotic state. Under the same coupling strength, when the friction is not considered, the vibration of tenon increases with the gap.

Fig. 3Response characteristics of tenon without friction

a)$k_c=\text{71}$, $\omega =\text{1}$, $d_0=\text{0.008}$

b)$\mathrm{}{k}_c=\text{16}$, $\omega =\text{1}$, $d_0=\text{0.008}$

c)$k_c=\text{71}$, $\omega =\text{1}$, $d_0=\text{0.8}$

d)$k_c=\text{16}$, $\omega =\text{1}$, $d_0=\text{0.8}$

3.1.2. Vibration response of tenon with friction between Tenon and mortise

When the coupling stiffness is strong coupling, the excitation frequency $\omega =\text{1}$ and the initial gap $d_0=\text{0.008}$ are selected.

When the coupling stiffness is strong coupling and small gap, the maximum amplitude is 1.0369, and there are 2-8 frequency doubling in the system response spectrum, among which the 2, 4, 5 frequency components are larger. There are irregular points in the section of the tenon Poincare, and the position of the unsmooth time-domain waveform may be caused by the influence of the second, fourth and fifth harmonic components. When the coupling stiffness is weak coupling and small gap, the maximum amplitude is 3.7074, and there are multiple frequency doubling phenomena in the system response spectrum, among which the second, fourth and sixth harmonic components are larger. There are irregular points in the section of the tenon Poincare, and the position of the unsmooth waveform in time domain may be caused by the influence of frequency components of 2, 4 and 6. When the coupling stiffness is strong coupling and large gap, the maximum amplitude is 1.0578, there are several frequency doubling phenomena in the system response spectrum, among which the second harmonic component is the largest. There are irregular points in the section of the tenon Poincare. When the coupling stiffness is weak coupling and large gap, the maximum amplitude is 4.3453, in which 2, 3, 4 SHG components are larger. There are irregular points in the Poincare section of Tenon and mortise, and the position of unsmooth waveform in time domain may be caused by the influence of frequency components of 2, 3 and 4. These characteristics indicate that the system is in chaotic state.

From the comparison between Fig. 3 and Fig. 4, it can be seen that when the coupling stiffness is strong coupling, the vibration amplitude of tenon is smaller than that of weak coupling, and when friction is not considered, the vibration amplitude of tenon is small regardless of whether the initial gap is small or large. When the coupling stiffness is weak coupling, the vibration amplitude of tenon is larger when the friction is considered.

Fig. 4Response characteristics of tenon with friction

a)$k_c=\text{71}$, $\omega =\text{1}$, $d_0=\text{0.008}$

b)$\mathrm{}{k}_c=\text{16}$, $\omega =\text{1}$, $d_0=\text{0.008}$

c)$k_c=\text{71}$, $\omega =\text{1}$, $d_0=\text{0.8}$

d)$k_c=\text{16}$, $\omega =\text{1}$, $d_0=\text{0.8}$

3.2. Effects of tenon gap and dry friction on blade vibration response of mistuned bladed disk

It can be seen from Fig. 5 and Fig. 6 that the maximum vibration amplitude of the mistuned blade is smaller than that without considering the friction force when the gap between tenon and groove and friction force are considered. When the coupling stiffness between disks is weak, the maximum amplitude of blades in the mistuned bladed disk system considering the friction between tenons and mortise is small. Compared with Fig. 5 and Fig. 6, it can be seen that the mistuning will change the vibration amplitude of the bladed disk system, and the existence of the mistuning factor makes the dynamic behavior of the bladed disk system more complex. The coupling strength has a great influence on the vibration amplitude of the blade, and the strong coupling makes the energy transfer between sectors strengthen, resulting in the increase of the vibration amplitude of the blade.

Fig. 5Blade vibration response amplitude of strongly coupled

a)$d_0=\text{0.008}$, without friction

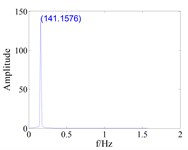
b)$d_0=\text{0.008}$, with friction

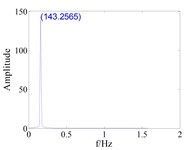
c)$d_0=\text{0.8}$, without friction

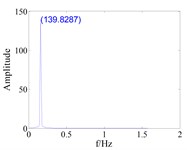
d)$d_0=\text{0.8}$, with friction

Fig. 6Blade vibration response amplitude of weak coupled

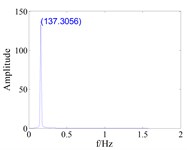
a)$d_0=\text{0.008}$, without friction

b)$d_0=\text{0.008}$, with friction

c)$d_0=\text{0.8}$, without friction

d)$d_0=\text{0.8}$, with friction

4. Effect of damping mistuning on vibration characteristics of mistuned bladed disk

4.1. Effect of blade equivalent damping mistuning on vibration characteristics of mistuned bladed disk

Considering the effect of blade equivalent damping mistuning on the vibration characteristics of bladed disk with different gap and coupling strength, the coupling stiffness of 16 and 71 is selected as the weak coupling and strong coupling, and the gap of 0.008 and 0.8 is selected as the small gap and large gap. Through analysis, the time domain waveform diagram, phase diagram, Poincare section and tenon frequency spectrum of tenon are obtained as shown in Fig. 7.

It can be seen from Fig. 7 that when the gap is the same, the vibration amplitude of the tenon is smaller than that of the weak coupling under strong coupling. In the case of strong coupling, when the gap is large, the vibration amplitude of the tenon is smaller than that when the gap is small. In the case of weak coupling, when the gap is large, the vibration amplitude of the tenon is larger than that of the small gap.

It can be seen from Fig. 8 and Fig. 9 that under the condition of the same gap, the vibration amplitude of the blade with strong coupling is larger; when the coupling stiffness and gap are the same, the equivalent damping mistuning of the blade body will increase the vibration amplitude of the blade, but the vibration amplitude of the blade will change slightly. The mistuning of damping leads to the enhancement of vibration energy transfer in each sector and the increase of blade vibration amplitude.

Fig. 7Effect of blade equivalent damping mistuning on vibration response of tenon

a)$k_c=\text{16}$, $d_0=\text{0.008}$

b)$\mathrm{}{k}_c=\text{71}$, $d_0=\text{0.008}$

c)$k_c=\text{16}$, $d_0=\text{0.8}$

d)$k_c=\text{71}$, $d_0=\text{0.8}$

Fig. 8Response of blade equivalent damping mistuning to blade vibration with small gap (d0=0.008)

a) Tuned, $k_c=\text{16}$

b) Mistuned, $k_c=\text{16}$

c) Tuned, $k_c=\text{71}$

d) Mistuned, $k_c=\text{71}$

Fig. 9Response of blade equivalent damping mistuning to blade vibration with large gap (d0=0.8)

a) Tuned, $k_c=\text{16}$

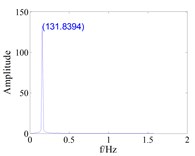
b) Mistuned, $k_c=\text{16}$

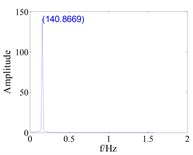
c) Tuned, $k_c=\text{71}$

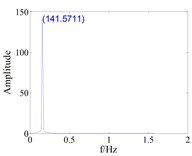
d) Mistuned, $k_c=\text{71}$

4.2. Effect of tenon equivalent damping mistuning on vibration characteristics of mistuned bladed disk

In the case of different coupling strength and gap, the frequency spectrum of the coupling diagram with strong coupling stiffness $k_c\text{=71}$ and weak coupling stiffness $k_c=\text{16}$ are selected respectively. The gaps of 0.008 and 0.8 were selected as small and large gaps, the effect of blade equivalent damping mistuning on the vibration response of tenon is obtained by analysis.

It can be seen from Fig. 10 that when the gap is the same, the vibration amplitude of the tenon is smaller than that of the weak coupling under strong coupling; in the case of strong coupling, when the gap is large, the vibration amplitude of the tenon is smaller than that when the gap is small; in the case of weak coupling, when the gap is large, the vibration amplitude of the tenon is larger than that of the small gap. It can be seen from the comparison of Fig. 4 and Fig. 10 that under the small gap, blade equivalent damping mistuning increases the vibration amplitude of tenon.

Fig. 10The effect of blade equivalent damping mistuning on the vibration response of tenon

a)$k_c=\text{16}$, $d_0=\text{0.008}$

b)$\mathrm{}{k}_c=\text{71}$, $d_0=\text{0.008}$

c)$k_c=\text{16}$, $d_0=\text{0.8}$

d)$k_c=71$, $d_0=\text{0.8}$

It can be seen from Fig. 11 and Fig. 12 that when the gap is large, the equivalent damping mistuning of the blade body will increase the vibration amplitude of the blade; when the gap is small, the equivalent damping mistuning of the blade body has little influence on the vibration amplitude of the blade.

Fig. 11The effect of tenon equivalent damping mistuning on the vibration response of blade with small gap (d0=0.008)

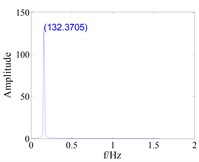
a) Tuned, ${\mathrm{k}}_{\mathrm{c}}=16$

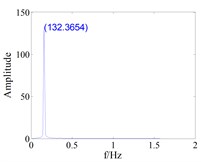
b) Mistuned, ${\mathrm{k}}_{\mathrm{c}}=16$

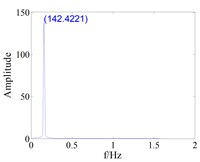
c) Tuned, ${\mathrm{k}}_{\mathrm{c}}=71$

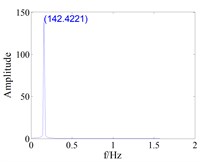
d) Mistuned, ${\mathrm{k}}_{\mathrm{c}}=71$

Fig. 12The effect of tenon equivalent damping mistuning on the vibration response of blade with large gap (d0=0.8)

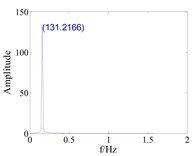
a) Tuned, $k_c=\text{16}$

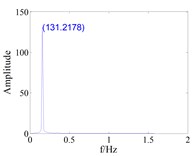
b) Mistuned, $k_c=\text{16}$

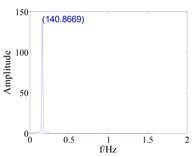
c) Tuned, $k_c=\text{71}$

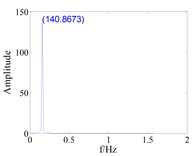
d) Mistuned, $k_c=\text{71}$

4.3. Effect of mistuning of tenon dry friction damping force on vibration characteristics of mistuned bladed disk

In the case of different coupling strength and gap, the frequency spectrum of the coupling diagram with strong coupling stiffness $k_c=$ 71 and weak coupling stiffness $k_c=\text{16}$ are selected respectively. The gaps of 0.008 and 0.8 were selected as small and large gaps, the effect of tenon dry friction damping mistuning on the vibration response of tenon is obtained by analysis.

Fig. 13Effect of tenon’s dry friction damping force mistuning on vibration response of tenon

a)$k_c=\text{16}$, $d_0=\text{0.008}$

b)$\mathrm{}{k}_c=\text{71}$, $d_0=\text{0.008}$

c)$k_c=\text{16}$, $d_0=\text{0.8}$

d)$k_c=71$, $d_0=\text{0.8}$

It can be seen from Fig. 13 that when the gap is the same, the vibration amplitude of the tenon is smaller than that of the weak coupling. When the coupling strength is strong and the gap is large, the vibration amplitude of the tenon is smaller than that the gap is small. In the case of weak coupling, when the gap is large, the vibration amplitude of the tenon is larger than that of the small gap. The gap has little effect on the vibration response of the weakly coupled bladed disk, but the gap has a great influence on the strongly coupled bladed disk, the larger the gap, the more complex the nonlinear dynamic characteristics of tenon. It can be seen from the comparison of Fig. 4 and Fig. 13 that under the same gap and coupling strength, the dry friction damping mistuning of tenon increases the vibration amplitude of tenon.

Fig. 14Response of blade vibration when tenon’s dry friction damping force mistuning under weak coupling (kc=16)

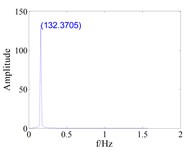
a) Tuned ${\mathrm{d}}_0=\text{0.008}$

b) Mistuned $d_0=0.008$

c) Tuned ${\mathrm{d}}_0=\text{0.8}$

d) Mistuned $d_0=0.8$

Fig. 15Response of blade vibration when tenon’s dry friction damping force mistuning under strong coupling (kc=71)

a) Tuned $d_0=\text{0.008}$

b) Mistuned $d_0=\text{0.008}$

c) Tuned $d_0=\text{0.8}$

d) Mistuned $d_0=\text{0.8}$

It can be seen from Fig. 14 and Fig. 15 that under the condition of the same gap, the vibration amplitude of the blade with strong coupling is larger; when the coupling stiffness and gap are the same, the tenon’s equivalent damping mistuning will increase the vibration amplitude of the blade, but the vibration amplitude of the blade will change slightly.

5. Conclusions

Aiming at the Tenon and mortise structure of aero-engine compressor bladed disk, a dynamic model including blade, tenon and disk was established. The nonlinear dynamic characteristics of bladed disk system with damping mistuning were studied.

1) The dynamic model and nonlinear vibration equation including blade body, tenon and disk are established. The effects of tenon gap and dry friction on the nonlinear dynamics of bladed disk are considered in the model.

2) Comparative analysis of the effects of tenon gap and dry friction on the vibration response of the mistuned bladed disk. The results show that the tenon gap and dry friction have a certain influence on the vibration response of the mistuned bladed disk, which cannot be ignored in the dynamic analysis.

3) The effects of blade equivalent damping and tenon equivalent damping mistuning on the vibration characteristics of bladed disk system are obtained: When the gap is the same, the vibration amplitude of the tenon is smaller than that of the weak coupling under the condition of strong coupling; The vibration amplitude of the tenon is smaller than that of the small gap under the condition of strong coupling; In the case of weak coupling, the vibration amplitude of tenon is larger than that of small gap when the gap is large.

4) The effects of the mistuning of the tenon’s dry friction damping force on the vibration characteristics of the mistuned bladed disk is obtained: Under the same gap, the blade vibration amplitude is larger when the coupling is strong; When the coupling stiffness and gap are the same, the equivalent damping mistuning of blade will lead to the increase of blade vibration amplitude, but the change of blade vibration amplitude is small.