Effect of Coriolis force on vibration localization characteristics of mistuned bladed disk

1. Introduction

Mistuning is a common phenomenon in aeroengine compressor bladed disk system. Mistuning results from inconsistent blade mass, stiffness and frequency caused by the material, manufacture and wear; mistuning will lead to serious vibration localization. When an aeroengine compressor bladed disk conducts the dynamic characteristics analysis, if the finite element model of the disk based on high fidelity engineering is adopted, the number of elements and nodes generated by the divided grid is larger, then the calculation is difficult. The blades and disk are connected with the structure of the tenon and mortise; and the contact state changes with rotation speed. The nonlinear contact of the blade tenon and disk mortise will strongly affect the amplitude [1-3] of the bladed disk vibration response; therefore, the analysis model of the bladed disk must consider the influence of the contact state of the tenon and mortise on the vibration of the blade and disk. However, the circumferential cyclic symmetry of the bladed disk structure is destroyed by mistuning, the cyclic symmetry cannot be adopted for analysis, and it is more time-consuming to analyse and calculate using the blisk model. If the contact relationship between the blade tenon and disk mortise is considered, the analysis will become more difficult.

Many scholars have studied reduced-order modeling, which is based on the finite element method. Hurty and Gladwell [4, 5] established modal coordinates and proposed the concept of a modal synthesis method. Craig and Bampton [6] proposed the fixed interface method (C-B method), Bladh, Castanier and Pierre [7, 8] proposed the SMART (Secondary Modal Analysis Reduction) method based on the C-B method. Thus, the degree of freedom of the model was further reduced. Craig and Chang [9, 10] proposed a substructure coupling method that is based on the free interface and discussed the substructure coupling problem, which is based on improving the substructure model. He [11] adopted the free interface mode synthesis method for the damping vibration system to calculate the residual flexibility matrix by the weighted orthogonal matrix. The inverse of the stiffness matrix can be avoided by using the weighted orthogonal matrix. Ying [12] proposed a substructure mixed interface modal synthesis method with a fixed interface and a free interface. The modal synthesis technique based on these two typical modes can accurately estimate the structural modal. Based on the mixed interface method, Bai [13, 14] proposed IHISCMSM (Improved Hybrid Interface Substructural Component Modal Synthesis Method). This method can further reduce the degree of freedom after synthesis. The parametric model of the blade + disk is established by this method and based on the overall model calculation efficiency and calculation error, the results show that the computational efficiency and computational error are clearly improved compared with the classical method. Beck [15] proposed two methods that Component-Mode Reduced-Order Models in integrally bladed rotors, the methods provide highly accurate results in a significant reduction in solution time compared to the full finite-element model and parent reduced-order model. Based on the cyclic-based harmonic balance method, Wang and Li [16] established a method for solving the entire bladed disk response using a single sector matrix. This method does not have truncation errors; therefore, it provides higher solution accuracy.

Many scholars have conducted extensive research on the vibration localization of mistuned bladed disk. Ewins [17] considers that mistuning causes the localization phenomenon of modal vibration modes. Wei and Pierre [18, 19] studied the influence of the bladed disk parameters on mode localization. Ottarsson and Pierre [20] adopted the transfer matrix method and Monte Carlo simulation method to study the free vibration localization of the mistuned bladed disk. On the basis of the lumped parameter model and finite element model, given the research on the mistuned vibration characteristics of bladed disk, in order to quantitatively evaluate the modal localization caused by the mistuning, the localization factor of the modal shape is defined by Wang , Yu and Liao [21-24] to describe the localization characteristic of the mistuned bladed disk structure. Wang [25] studied the randomly mistuned characteristics of the group bladed disk and analysed the relationship between the mistuned sensitivity and mistuned intensity using the lumped parameter model and Monte Carlo analysis method. He and Wang [26, 27] systematically analysed the random mistuning response of the random mistuned disk system using the Monte Carlo method under different coupling strengths, especially under moderate coupling strength.

Nikolic [28] studied the influence of the interaction between Coriolis force and mistuned blade on the vibration characteristics of mistuned disk; furthermore, the author analysed and compared the influence of Coriolis force on the vibration of mistuned bladed disk in the case of different forced response mistuned degrees and amplitude magnification factors. Ma [29] adopted the ANSYS software for compressor blades to discuss the influence of centrifugal stiffening and other parameters on blade vibration characteristics.

However, the centrifugal force of the bladed disk at high speed rotation will produce a prestress effect, which is caused by the centrifugal force that has considerable influence on the natural frequency of the bladed disk. Therefore, the effect of prestress cannot be ignored in the analysis of the dynamic characteristics of the rotating machinery. In addition, the Coriolis force also has a certain influence on the natural frequency and vibration mode of the bladed disk at the high speed rotation. At present, most scholars mainly focus on the influence of the vibration characteristics when studying the Coriolis force influence on the mistuned bladed disk; therefore, fewer studies have investigated the influence of the Coriolis force on the vibration localization of the mistuned bladed disk.

On the basis of the substructures modal synthesis method for the fixed interfaces, this paper considered the effect of the centrifugal force and the Coriolis force, the component mode synthesis method for the fixed interfaces was established. Adopting this method, the finite reduced order models of the bladed disk were established. The effect of the centrifugal force and the Coriolis force on the vibration localization characteristic of the harmonic and the mistuned blades disk was discussed, and the effect of the centrifugal force and Coriolis force was analysed, which are under the different mistuned patterns and engine order of excitation on the vibration localization characteristics of the mistuned bladed disk.

2. Component mode synthesis method for fixed interface

C-B method is well known for fixed interface modal synthesis method, it was proposed by Craig and Bampton. This method has been studied and improved by many scholars and has gradually matured in recent years. The substructure mode reduced-order principle of the modal synthesis method for fixed interfaces is based on two groups of modes to represent the substructure motion. One group of modes is a reduced mode set fixed for the substructure interface degree of freedom, and the other is a complete set of constraint modes that include the element deformation in an interface degree of freedom but fixed deformation in all other interface degrees of freedom. This article is based on the modal synthesis method for a fixed interface, and it’s considered the influence of the centrifugal force and Coriolis force; furthermore, this article established a finite reduced-order model of the bladed disk with the modal synthesis method for a fixed interface. The model of the bladed disk is shown in Fig. 1. The material properties of the model are listed in Table 1.

Fig. 1The model of bladed disk

a) The model of bladed disk

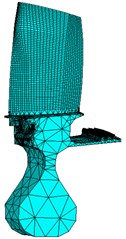
b) The substructure model of bladed disk

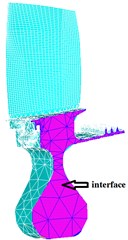
c) The interface of bladed disk

The compressor bladed disk system is assembled with 38 blades, each blade is composed of a blade body and a tenon, the blades and disk are connected through the tenon and mortise to form a bladed disk system. When the aeroengine compressor blades under centrifugal force, the natural frequency and dynamic response of the structure will be affected, considering the influence of the centrifugal stiffening effect of the rotor system on the dynamic characteristics. the equation of $i$th blade that considered the centrifugal force effect can be expressed as:

where $[M{]}_i$ is the mass matrix, ${\left[C\mathrm{\text{'}}\right]}_i$ is damping matrix, $[K\mathrm{\text{'}}{]}_i$ is stiffness matrix that considered centrifugal force and Coriolis force, $\{F{\}}_i$ is the force acting on the substructure model, and $\{X{\}}_i$ is the displacement vector, where:

$C$ is damping matrix, and $G$ is Coriolis force matrix, where:

where $f_{n1}$ and $f_{n2}$ are the first-order and second-order natural frequencies, respectively, ${\xi }_1$ and ${\xi }_2$ are the corresponding modal damping ratios.

The Coriolis force matrix is generated as:

where $N$ is the shape function matrix; $n$ is the total number of elements; $\mathrm{\Omega }$ is the rotational matrix:

where $K$ is the stiffness matrix of the structure, $K_c$ is the centrifugal stiffening effect matrix of the rotating blades, and $K_S$ is the rotation-softening matrix.

For aeroengines and others rotating machinery that are under the effect of centrifugal force, the natural frequency and dynamic response of the rotating components will have a certain influence compared with the static equipment. Therefore, the centrifugal load should be transformed to the centrifugal force effect matrix; thus, the equation considering the centrifugal force effect is obtained.

The displacement vector $\{X{\}}_i$ is composed of the degree of freedom $X_m$ at the boundary and internal freedom $X_s$ of the non-interface, where $m$ is the interface DOF of the blades and disk, $s$ is the internal DOF of the blades and disk in Fig. 1, that is:

Eq. (1) can be expressed as:

where $f_m$ is the interface force. Let the substructure of the interface be fixed, even if $X_m=0$, which can obtain:

From this Eq. (9), the normalized mode $\left[{\varphi }_N\right]$ is solved, that is $\left[{\varphi }_N\right]=[{\varphi }_l,{\varphi }_h]$, where $\left[{\varphi }_l\right]$ –low order modal matrix, $\left[{\varphi }_h\right]$ – high order modal matrix.

This modal set satisfies the following conditions:

where $\left[{\mathrm{\Lambda }}_l\right]=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\lambda }_1^2,{\lambda }_2^2,\cdots ,{\lambda }_l^2\right)$, $\left[{\mathrm{\Lambda }}_h\right]=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\lambda }_{l+1}^2,{\lambda }_{l+2}^2,\cdots ,{\lambda }_h^2\right)$, and $I$ is an identity matrix.

When analysing the vibration modal of the bladed disk, the low order mode is mainly studied, the higher order mode sets are omitted, and the lower order mode set ${\varphi }_l$ is selected to form the master modal set ${\varphi }_m$ of the substructures, that is:

If the fixed interface method [7, 8] is used, ${\varphi }_J$ can be expressed as follows:

Definition $\left[{\varphi }_c\right]$ is the constrained modal set:

The Ritz base vector of the I substructure is:

The coordinate transformation is:

Eq. (16) can transform the equation of motion from physical coordinates to modal coordinates:

where ${\left[\stackrel{-}{M}\right]}_i={\left[\varphi \right]}^T{\left[M\right]}_i\left[\varphi \right]$, ${\left[\stackrel{-}{C}\right]}_i={\left[\varphi \right]}^T{\left[C\mathrm{\text{'}}\right]}_i\left[\varphi \right]$, ${\left[\stackrel{-}{K}\right]}_i={\left[\varphi \right]}^T{\left[K\mathrm{\text{'}}\right]}_i\left[\varphi \right]$, ${\left[\stackrel{-}{F}\right]}_i={\left[\varphi \right]}^T{\left[F\right]}_i$.

The coordinates transformation of Eq. (16) uses only low order mode, ignores the high order mode, and adapts the mode truncation; therefore, the node degree of freedom is greatly reduced. The result will be constituted as the $i$ substructure formula obtained by Eq. (16):

If the rigid connection interface is considered, through the force balance and displacement compatibility, the following can be obtained:

The non-independent coordinate can be transformed to the equation of motion of the generalized coordinate $\left\{q\right\}$ by the following form:

that is:

Eq. (17) is transformed to the equation of motion of the generalized coordinate by using this form $\left\{q\right\}$:

where ${\left[\tilde{M}\right]}_i={\left[\beta \right]}^T{\left[\stackrel{-}{M}\right]}_i\left[\beta \right]$, ${\left[\tilde{K}\right]}_i={\left[\beta \right]}^T{\left[\stackrel{-}{K}\right]}_i\left[\beta \right]$, ${\left[\tilde{C}\right]}_i={\left[\beta \right]}^T{\left[\stackrel{-}{C}\right]}_i\left[\beta \right]$, ${\left[\tilde{F}\right]}_i={\left[\beta \right]}^T{\left[\stackrel{-}{F}\right]}_i$.

Eq. (23) can be adopted to solve the natural frequency of the system and the vibration mode under the generalized coordinates $\left\{q\right\}$. The vibration mode under the generalized coordinates can be returned to the physical coordinates by the coordinate transformation Eq. (23) and form Eq. (16); thus, the vibration mode of the system physical coordinates can be obtained. In practical applications, because the higher-order modals of the main interface modal $\left[\varphi \right]$ are omitted, only certain low order modals are taken; thus, the size of analyses and calculations are greatly reduced.

Based on component mode synthesis methods for fixed interface, the mistuned bladed disk is analysed. The centrifugal force produced by the centrifugal force under high speed rotation of the aeroengine compressor bladed disk system affects the natural frequency of the bladed disk. The calculate results are shown in Fig. 2 and Table 2.

Fig. 2The natural frequencies of the bladed disk with the centrifugal force effect

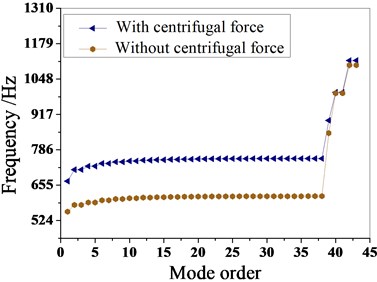
Fig. 3The effect of Coriolis force on the dynamic frequency

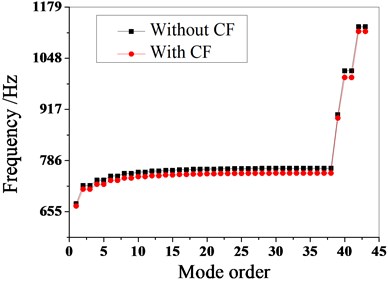
Fig. 2 is the dynamic frequency comparison obtained by the modal analysis of the bladed disk Whether to consider the centrifugal force effect. It can be seen from the figure that the influence of the centrifugal force effect on the dynamic frequency of the bladed disk is remarkable. In the actual analysis, the effect of the centrifugal force on the vibration of the bladed disk cannot be ignored. From Table 2, it can be seen that whether centrifugal force is taken into account has a significant effect on the calculation accuracy, and the maximum error can reach 18.5 %, the minimum calculation error is 16.9 %. In summary, the effect of centrifugal force cannot be neglected when calculating the dynamic response of the rotating bladed disk system.

The blades of the aeroengine compressor bladed disk system and other dynamic machinery are inevitably affected by the Coriolis force during operation. The influence of Coriolis force of the vibration characteristics of the bladed disk should be further studied. In this article, the influence of considering the Coriolis force on the vibration characteristics of the bladed disk is studied on the basis of the modal synthesis method for a fixed interface and finite element reduced-order models. Table 3 and Fig. 3 are the effect of the CF (Coriolis force) on the dynamic frequency.

From Fig. 3, it can be seen that the dynamic frequency of the bladed disk without considering the Coriolis force effect is larger than that of the bladed disk considering the Coriolis force softening slightly rotation effect, and it can be seen that the Coriolis force effect can reduce the dynamic frequency of the disk system. From Table 3, it can be seen that the calculation error caused by the effect of the Coriolis force is not more than 2 %. Although the error is small, for aeroengine compressor bladed disk system, a small difference in the amplitude of each blade can cause vibration localization, Therefore, the effect of the Coriolis force on the vibration characteristics of a bladed disk system cannot be neglected in the analysis of dynamic characteristics.

3. Effect of Coriolis force on vibration localization characteristics of mistuned bladed disk

The equation of tuned bladed disk can be expressed as:

Under the circumstance of only considering stiffness mistuning, the kinetic equation of the mistuned bladed disk can be expressed as:

where $\mathrm{\Delta }K$ is the stiffness mistuning matrix, and the $i$-th component of the travelling wave exciting force $F$ can be expressed as:

where $F^0$ is the vibration amplitude of the exciting force load by $i$th rotor blade, $\omega$ is the excitation frequency, ${\phi }_i$ is the phase angle of the travelling wave exciting force on the $i$th blade, as follows:

where $E$ is the engine order of excitation.

3.1. Effect of Coriolis force on vibration characteristics of tuned bladed disk

Under differents engine order of excitation, by calculating whether to consider the effect of the Coriolis force on the amplitude of the tuned bladed disk, the results shown in Fig. 4 are obtained. The figure shows that the maximum amplitude of the bladed disk without considering the Coriolis force effect is larger than with it. Regardless of whether to consider softening, the maximum amplitude of the tuned bladed disk tends to gradually increase with the increase of the engine order of excitation.

Fig. 4The maximum amplitude of the tuned bladed disk with and without Coriolis force

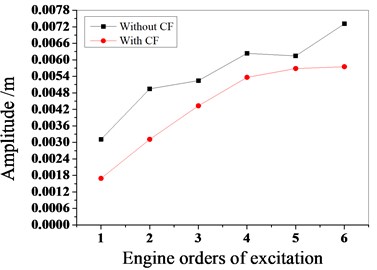
Fig. 5Vibration characteristics of tuned bladed disk with and without Coriolis Force when E is 4

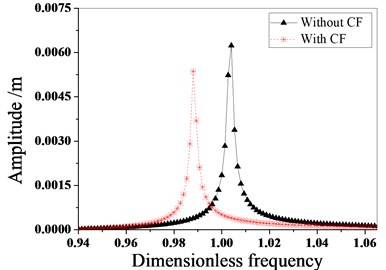
a) Amplitude frequency characteristics

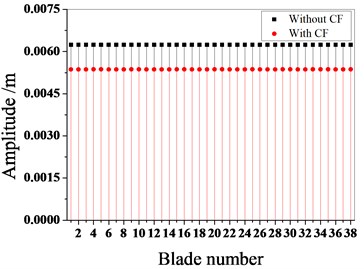
b) Maximum amplitude of blades

Fig. 5 illustrates whether to consider the influence of the Coriolis force on the amplitude frequency characteristics of the bladed disk when the engine order of excitation is 4. As shown in the figure, when considering softening, the frequency of the maximum amplitude of the tuned bladed disk decreases, and the maximum amplitude also decreases considerably. It can be seen that the Coriolis effect influences the frequency characteristics of the tuned bladed disk. Fig. 6 is the distribution of deformation in the case of whether or not the Coriolis force is taken into account.

Fig. 6Deformation distribution of tuned bladed disk

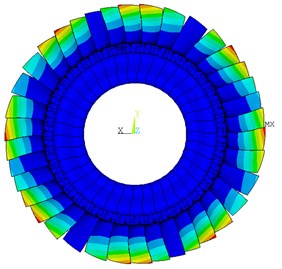
a) Without Coriolis force

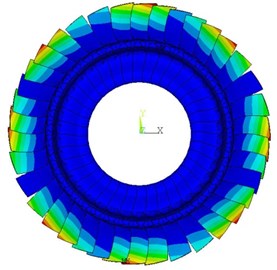
b) With Coriolis force

3.2. Effect of Coriolis force on vibration localization characteristics of mistuned bladed disk

In order to analyze the effect of the Coriolis force on the vibration localization of mistuned bladed disk, two typical mistuned modes and three random mistuned modes are used to simulation analysis.

Fig. 7Typical mistuning value of blades

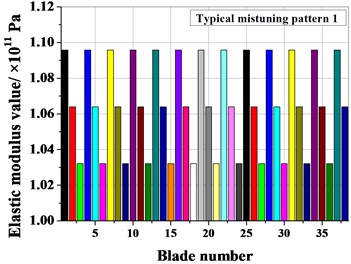
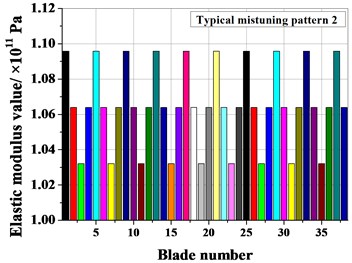
Fig. 8Amplitude frequency characteristics of mistuned bladed disk with and without Coriolis force

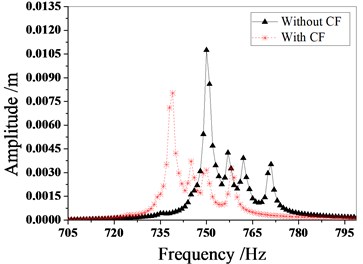
a) Typical mistuning pattern 1

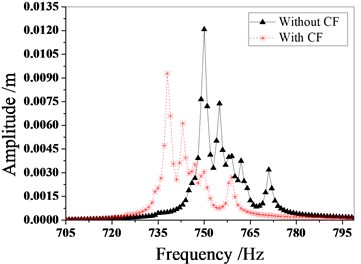
b) Typical mistuning pattern 2

Fig. 7 shows the typical mistuning value of the blades, and Fig. 8 shows the vibration response characteristics of the typical mistuning bladed disk system with or without considering the Coriolis force. Fig. 9 shows the effect of the Coriolis force on the maximum amplitude of the typical mistuned blade. Figs. 10 and 11 show the effect of the Coriolis force on the amplitude distribution of two typical mistuned pattern.

Fig. 9Maximum amplitude of blades with and without Coriolis force

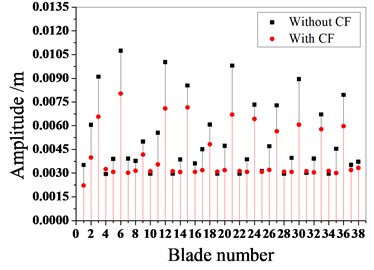
a) Typical mistuning pattern 1

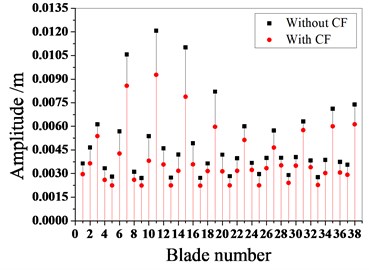
b) Typical mistuning pattern 2

Fig. 10Deformation distribution of typical mistuning pattern 1

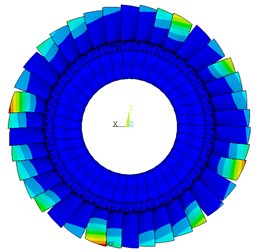
a) Without Coriolis force

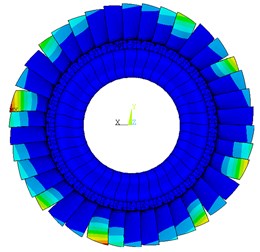
b) With Coriolis force

Fig. 11Deformation distribution of typical mistuning pattern 2

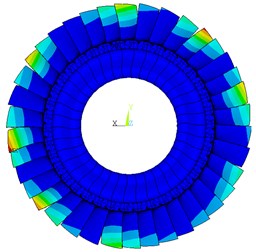
a) Without Coriolis force

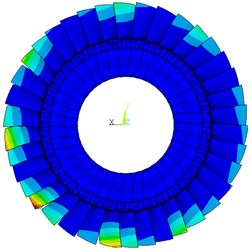
b) With Coriolis force

When considering only stiffness mistuning, the blade shows mistuning according to the experimental data. The blade mistuning value of the three types of mistuned patterns is obtained, as shown in Fig. 12, by the mistuned identification for the elastic modulus of the blade.

Fig. 13 and Fig. 14 are the amplitude frequency characteristics of the bladed disk under three mistuned patterns and the maximum amplitude distribution of each blade. It can be seen from the figure that regardless of the mistuned patterns, the amplitude of mistuned bladed disk is small with Coriolis force. The resonance frequency also decreases, but the trend of the amplitude frequency characteristic curve is the same.

Fig. 12Mistuning value of blades

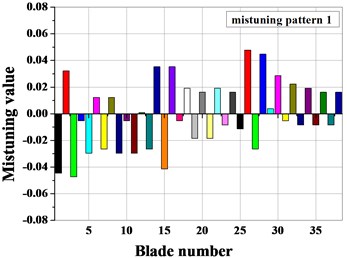
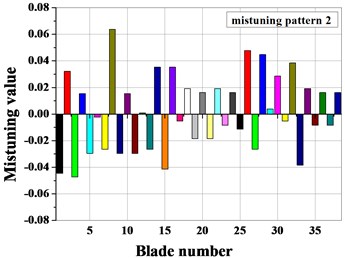
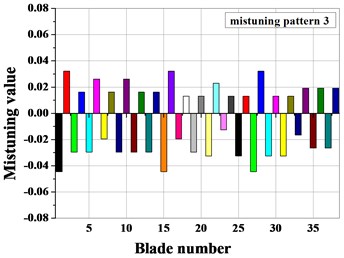
Fig. 13Amplitude frequency characteristics of mistuned bladed disk with and without Coriolis force

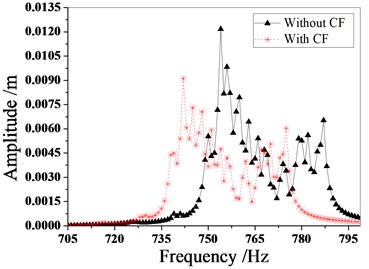
a) Mistuned pattern 1

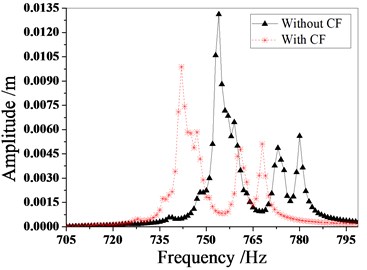
b) Mistuned pattern 2

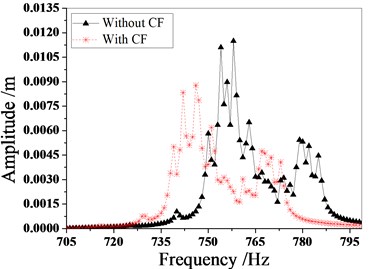
c) Mistuned pattern 3

Fig. 14Maximum amplitude of blades with and without Coriolis force

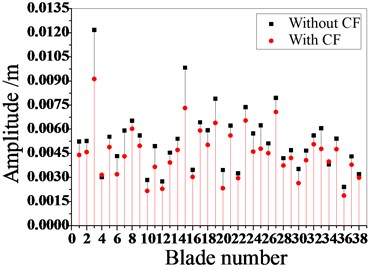
a) Mistuned pattern 1

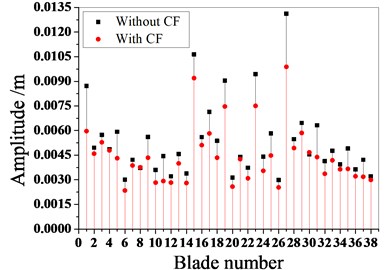
b) Mistuned pattern 2

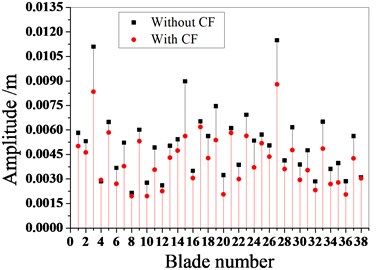
c) Mistuned pattern 3

Fig. 15The vibration localization characteristics of the mistuned bladed disk

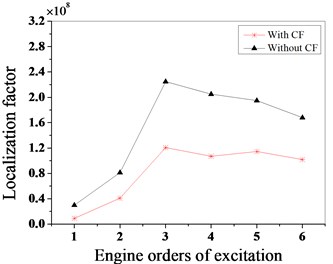
a) Mistuned pattern 1

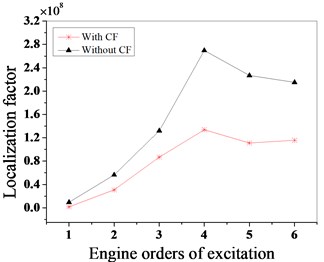
b) Mistuned pattern 2

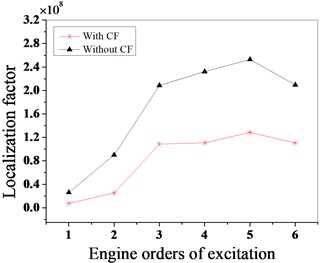
c) Mistuned pattern 3

The vibration localization factor in the literature [30] is an important indicator to evaluate the vibration characteristics of mistuned bladed disk. To analyze the influence of the Coriolis force on the vibration localization of the mistuned bladed disk, the vibration localization factor is adopted. The below equation for calculating this factor:

28

$L=\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(X\right)\times \mathrm{v}\mathrm{a}\mathrm{r}\left(X\right),$

where, $X$ – maximum amplitude vector of each blade, $\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(X\right)$ is the mean of maximum amplitude of each blade, $\mathrm{v}\mathrm{a}\mathrm{r}\left(X\right)$ is the maximum amplitude variance of each blade.

The vibration localization characteristics of the bladed disk under three mistuned patterns are analyzed by this factor. As shown in Fig. 15, the maximum localization factor appears in the mistuned pattern 1 when the engine order of excitation is 3, 4 in mistuned pattern 2; and 5 in mistuned pattern 3. When considering the Coriolis force effect, the localization degree of the bladed disk is lower than without considering it.

4. Conclusions

This paper is the first to describe the effect of the Coriolis force effect on the vibration localization of a mistuned bladed disk. The mistuned bladed disk model was established by the mode synthesis method for fixed interface. By analyzing the effect of the centrifugal force and Coriolis force on the vibration localization characteristics of the mistuned bladed disk, the significance of this study to engineering and conclusions as follow:

1) The calculation problem with a large number of elements and nodes can be solved by the mode synthesis method for fixed interface, this method can greatly reduce the calculation time.

2) The centrifugal force has a significant effect on the calculation results, and the maximum error can reach 18.5 %. The minimum calculation error is 16.9 %. When considering the centrifugal force effect, the vibration frequency of the bladed disk is larger than without consideration, and the effect of the centrifugal force cannot be ignored when the dynamic response of the rotation bladed disk is calculated.

3) Although the calculation error of the dynamic frequency of the bladed disk caused by the Coriolis force is not more than 2 %, but it has a significant effect on the vibration localization of mistuned bladed disk system.

4) The Coriolis force has a different effect on the vibration localization degree of the bladed disk system with the engine order excitation and mistuned patterns. This paper provides a method for engineering calculation to analyze the localization degree under different mistuning modes and engine order excitation.