Effect of gait on the energy consumption of walking robots

S. Briskin, Eugene; V. Kalinin, Yaroslav

Vibroengineering Procedia

Browse Procedia

Published: 07 October 2016

Check for updates

Effect of gait on the energy consumption of walking robots

Eugene S. Briskin¹

Yaroslav V. Kalinin²

^{1, 2}Volgograd State Technical University, Volgograd, Russia

Corresponding Author:

Yaroslav V. Kalinin

Cite the article Download PDF

Downloads 1385

Abstract

The energy consumption of walking robots has been considered on the base of solution of variational problem. It is fixed that the gait is affected on the energy efficiency and must vary with speed.

1. Introduction

One of the problems of walking robots is their low energy efficiency. It is known [1] that energy consumptions grow in proportion to the cube of speed when walking robot moves with constant velocity of its body. This is due with the periodic acceleration and deceleration of unbalanced walking mechanisms in the transfer phase from one position to another. The use of energy recovery allowing to accumulate energy in the braking phase of the walking mechanism in the transfer and then to give it in the phase of accelerating, allows to increase the energy efficiency [2].

It is known methods to improve energy efficiency at the expense of motion comfort as bipedal [3] and multilegged robots [4]. For multilegged robots with dual walking mechanisms resulting equation gives you the opportunity to choose such law of motion, which ensures low energy consumption [5]. This equation for walking movers operating from a common motor has a form:

1

\dot{T} + Q V = Q_{a} V_{a},

where $T$ is kinetic energy of robots body and its movers; $Q$ , $V$ , $Q_{a}$ , $V_{a}$ - according resistance force and the velocity of the body translational motion in the current time and their average values in the one cycle.

In the general case the Eq. (1) is nonlinear differential equation of the second order with respect to the coordinates.

2. Statement of the problem

As we know there is a fairly complete classification of possible gaits of multilegged walking robots during their translational motion with rectilinear and uniform motion of body center of mass. The ratio mode $γ$ is the important element of classification:

2

γ = \frac{τ - t_{i}}{τ},

where $t_{i}$ is the time spent of walking mechanism in the phase of interacting with supported surface, $τ$ is total cycle time.

The another important feature is the time $τ_{j}$ of the start transfer of $j$ mover to a new position. The countdown is since the beginning of shifting phase of one of the walking mechanism.

This mechanism is considered as baseline $τ_{j}$ = 0.

Given that of the beginning and end of the transfer, $j$ mover it absolute speed:

3

{\dot{x}}_{j} = 0,

the motion of the body is performed without sliding of its pads on the ground.

The possible dependence ${\dot{x}}_{j} = {\dot{x}}_{j} (t)$ are shown in the Fig. 1.

Fig. 1Velocities of movers for example gait (τ = 0.5 second): 1 – The baseline walking mechanism τj = 0, 2 – j walking mechanism in case τj > 0, 3 – j walking mechanism in case τj < 0.

Velocities of movers for example gait (τ = 0.5 second): 1 – The baseline walking mechanism τj = 0, 2 – j walking mechanism in case τj > 0, 3 – j walking mechanism in case τj < 0.

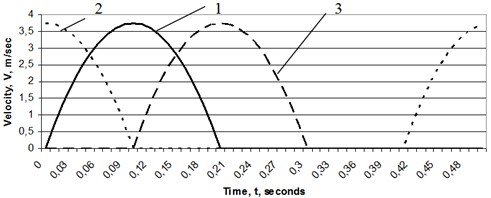
The simplest analytical dependence of the absolute speed ${\dot{x}}_{j}$ with time and satisfying the set conditions in Eq. (3) has the form:

4

{\dot{x}}_{j} = \{\begin{array}{l} - \frac{6 S}{t_{i}^{3}} {(t - τ_{j})}^{2} + \frac{6 S}{t_{i}^{2}} (t - τ_{j}), & τ_{j} < t < τ_{j} + t_{i}, \\ 0, & t < τ_{j}, t > τ_{j} + t_{i}, \end{array}

5

{\dot{x}}_{j} = \{\begin{array}{l} - \frac{6 S}{t_{i}^{3}} {(t - τ_{j})}^{2} + \frac{6 S}{t_{i}^{2}} (t - τ_{j}), & τ + τ_{j} < t, t < τ_{j} + t_{i}, \\ 0, & τ_{j} + t_{i} < t < τ_{j} + τ, \end{array}

where $S$ is the distance at which the walking mechanism pad is transferred over time $τ - t_{i}$ .

The main goal of submitted paper is to define such a low of rectilinear motion of the robot center of mass during its forward motion which provides the minimum of total heat losses all engines that control motion of all movers at various gaits and speeds.

3. Design scheme and mathematical model of walking robot

The translational motion of walking robot body of mass $M$ and $N$ its movers of mass $m$ each are studied. These motions are described by absolute coordinates $x_{c}$ , $x_{j}$ (Fig. 2) at that $a_{j}$ – coordinate of $j$ mover installation, $z_{j}$ – coordinate $j$ mover with respect to the point of its installation.

Fig. 2Design scheme of walking robot

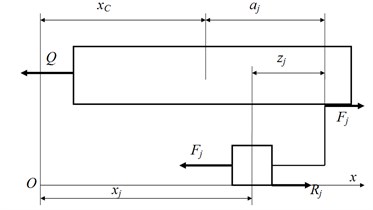
The resistance force $Q$ and forces of interactions between the body of walking robot and their movers $F_{j}$ are generated by drives of the course motion. The interaction of $j$ mover with supported surface is taken into account by tangent forces $R_{j}$ . The supported surface is modeled by homogeneous elastic medium and the body of the robot is modeled by absolutely solid. For this reason, all reactions $R_{j}$ for movers interacted with a ground are equal each other:

6

R_{j} = R .

Then the differential equations, described the motion of considered mechanical system have a form:

7

M {\ddot{x}}_{c} = \sum F_{j} - Q, j = 1,2, \dots, N,

0 = R - F_{j}, j = 1,2, \dots, k,

m {\ddot{x}}_{j} = - F_{j}, j = k + 1, k + 2, \dots, N,

where $N$ is the total number of movers, $k$ is the number of movers interacted with the support surface in a given moment of time and dependent on the gait. It follows from Eq. (7) that the force, generated by actuator is determined from second equation for movers interactive with the support surface and for movers which are in phase of transfer the force is determined from third. The constant force $R$ is determined from the first Eq. (7):

8

R = \frac{M {\ddot{x}}_{c} + Q + \sum_{j = k + 1}^{N} m {\ddot{x}}_{j}}{k} .

The feature of the Eq. (8) is the fact that in the process of motion a number of movers $k$ interact with the supporting surface may change. Hence considered mechanical system is system of variable structure.

4. Method of solution

In accordance with the task the method of solution is based on the requirement of the minimum of integral.

9

I_{*} = \int_{0}^{τ} \sum_{j = 1}^{N} F_{j}^{2} d t .

It is taken into account the isoperimetric condition:

10

\int_{0}^{τ} {\dot{x}}_{c} d t = S,

where $S$ is the distance, traversed by the body of robot during the time of interacting of walking mechanism with a supported surface.

Then we can obtain a new functional $I$ by combining Eq. (9) and Eq. (10):

11

I = \int_{0}^{τ} (\sum_{j = 1}^{N} F_{j}^{2} + μ {\dot{x}}_{c}) d t = \int_{0}^{τ} Φ d t .

12

Φ = \sum_{j = 1}^{k} {(\frac{M {\ddot{x}}_{c} + Q + \sum_{j = k + 1}^{N} m {\ddot{x}}_{j}}{k})}^{2} + \sum_{j = k + 1}^{N} {(m {\ddot{x}}_{j})}^{2} + μ {\dot{x}}_{c},

where $μ$ is undetermined Lagrange multiplier.

Since ${\ddot{x}}_{j}$ are defined as time function Eq. (4) and Eq. (5) and parameters $S$ , $t_{i}$ , $τ_{j}$ , the Euler-Poisson equations [6], providing the minimum of functional has a form:

13

\frac{d}{d t} (\frac{\partial Φ}{\partial {\ddot{x}}_{c}}) - \frac{\partial Φ}{\partial {\dot{x}}_{c}} = C,

or in expended form:

14

2 \frac{M^{2}}{k} {\overset{⃛}{x}}_{c} + 2 \frac{M}{k} \sum_{j = k + 1}^{N} m {\overset{⃛}{x}}_{j} = μ + C,

where $C$ is arbitrary constant.

The Eq. (14) must satisfy the initial and final conditions:

15

x_{c} (0) = 0, x_{c} (τ) = S, {\dot{x}}_{c} (0) = {\dot{x}}_{c} (τ) = V_{0},

which allow to determine three arbitrary constants of differential equation and the amount $μ + C$ , $V_{0}$ – initial and final velocity of robot’s body in each cycle.

One more peculiarity of Eq. (14) is dependence of the amount $k$ of movers interacting with a support surface from the gait.

5. Examples of the influence of gait on energy efficiency

The real walking robot “Ortonog” [7] (Fig. 3) have been considered as example of walking robot.

Fig. 3Walking robot “Ortonog”

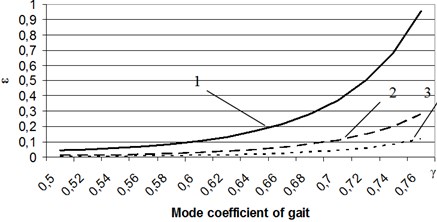
For this robot four mechanisms of walking always are interacted with the support surface. It is considered a such gait when the interacting with a support surface is carried out in pairs of two mechanisms of walking with ratio mode $γ$ > 0.5. It is presented on chart in Fig. 4 the dimensionless parameter $ε$ :

16

ε = \frac{I}{m^{2} g^{2} τ},

where $ε$ is parameter proportional energy losses, depending on ratio mode and average speed of robot, $g$ is acceleration of gravity.

The results show us that in order to minimize the energy consumption it is necessary to change the gait. This is confirmed by theory of synchronization [8], behavior of animals and investigation of multilegged walking machines and robots motion [9].

Fig. 4Dependencies of the rate of energy loss of walking robot’s speed and gait 1 – V0 is 0.5 m/s, 2 – V0 is 0.33 m/s, 3 – V0 is 0.25 m/s

6. Conclusion

The gait of walking robot significant effects on the energy consumption. For each speed you should choose energy optimal gait, but the most effective use of such actuator together with control system which could independently change the gait.

References

Ohotsimsky D. Е., Platonov A. K., Kiril’chenko А. А., Lapshin V. V. Schagayuschie Maschiny (Walking Machines). Preprint IPM of M.V. Keldysch AN USSR, Moscow, 1989, (in Russian).

Search CrossRef
Lapshin V. V. Modelnye Ocenki Energozatrat Schagayuschego Apparata (Model Estimates of Energy Walking Machine). Izvestia RAS, МТТ (News of RAS. Mechanics of Solid Body), Vol. 1, 1993, p. 65-74, (in Russian).

Search CrossRef
Beletskiy V. V. Dvunogaya Hod’ba: Model’nye Zadachi Dinamiki i Upravleniya (Biped Walking: Modeling Problems of Dynamics and Control). Science, Moscow, 1984, (in Russian).

Search CrossRef
Briskin Е. S., Kalinin Ya V. On energetically efficient algorithms of walking machines with cyclic drives. Journal of Computer and Systems Sciences International, Vol. 50, Issue 2, 2011, p. 348-354.

Search CrossRef
Briskin Е. S., Chernyschev V. V., Kalinin Ya. V., Маloletov А. V. On the energy efficiency of cyclic mechanisms. Mechanic of Solids, Vol. 49, Issue 1, 2014, p. 11-17.

Search CrossRef
Halfman R. L. Dynamics. Addison-Wesley Publishing Company, Inc. Reading, Massachusetts, Palo Alto, London, 1962.

Search CrossRef
Briskin Е. S., Maloletov А. V., Sharonov N. G., Fomenko S. S., Kalinin Ya. V., Leonard А. V. Development of rotary type movers discretely interacting with supporting surface and problems of control their movement. Proceedings of the 21st CISM-IFToMM Symposium on Robot Design, Dynamics and Control, Udine, Italy, 2016, p. 351-359.

Search CrossRef
Blekhman I. I. Synchronization in Science and Technology. ASME Press, New York, 1981.

Search CrossRef
Briskin Е. S. Ob Obschei Dinamike i Povorote Shagayuschih Mashin (On General Dynamics and Turns of Walking Machines). Problemy Mashinostroeniya i Dinamiki Mashin (Problems of Engineering and Reliability of Machines), Vol. 6, 1997, p. 33-39, (in Russian).

Search CrossRef

About this article

Received

07 September 2016

Accepted

12 September 2016

Published

07 October 2016

SUBJECTS

Oscillations in biomedical engineering

Keywords

walking robot

walking mechanism

energy efficiency

energy consumption

heat losses

variational problem

gait of walking robot

Acknowledgements

The work was supported by the RFBR (Grants Nos. 14-01-00655-A, 14-08-01002-A) and by Grant of Ministry of Education and Science of Russian Federation No. 862.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.