Investigation of the mechatronic system oscillatory motion with discrete feedback PD-control

1. Introduction

Nowadays digital measuring the position of links by use of encoders is widely used in automatic robot control systems. The feature of such principle is the discrete character of information entering the system’s regulator, which has significant influence on the accuracy of the actuating link and in some cases lead to the loss of stability [4-6]. One example is the oscillatory nature of the movement of actuating links of an exoskeleton described in papers [1-3].

Some papers [10, 11] are dedicated to the study of the influence of the parameters of the discrete negative feedback channel. A feature of this work is the study of the influence of the parameters of the discrete angle encoder in the negative feedback channel of the control system on regulator performance, overshoot and stability of the system on the basis of computational experiments with the mathematical model of the mechatronic system.

2. Description of the analytical model of the mechatronic system

At Fig. 1 an analytical model of the studied electromechanical system consisting of mass 1 fixed on link 2 is shown. The link is set into motion by an electric drive consisting of DC motor 4 (Maxon RE 35, 90W) and gear unit 3 (planetary Maxon GP 42, 113:1; bevel gear speed reducer with gear ratio 3.42:1) and rotational encoder 5.

Fig. 1Calculating scheme of the mechatronic system with feedback

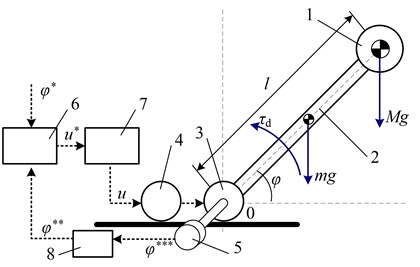
Presented system operates in the following way. The control signal with the desired angle ${\phi }^{*}$ and data from digital converter, which converts the continuous signal from the sensor 5${\phi }^{***}$ into a digital signal ${\phi }^{**}$ enter into control system, which includes the regulator and comparator 6. The regulator generates the output signal $u^{*}$, which enters power amplifier 7, from which the control voltage, $u$ enters electric drive 4 and link moves through an angle $\phi$.

The following denotations are used: $M$ – is the mass if the body fixed on the link, $m$ – mass of the link, $l$ – length of the link, ${\tau }_d$ – actuator torque.

3. Mathematical model of the mechatronic system

The mathematical model of the discussed system is presented with following assumptions: the links of the system are absolutely rigid; gaps in the gear unit are negligible, magnetic flux saturation is not considered during modelling.

Then, the system of equations describing the processes taking place in the mechatronic system is given as follows:

where the actuator torque ${\tau }_d$, acting on the system, are described in this case by the Eq. (2):

The following denotations are used in the given formulas: $J$ – reduced moment of inertia of the system:

$I$ – current in the coils of the core of the electric motor; $R$ – active resistance of the coils of the core; $i_r$– total gear ratio; $\eta$ – coefficient of efficiency of the mechanical transmission; $c_M$ – motor torque coefficient; $c_E$ – coefficient of the back EMF electric motor.

3.1. Structure of the control system

In order to construct a mathematical model of the negative feedback channel let us look at the block diagram of the control system (Fig. 2).

Fig. 2Block diagram of the control system

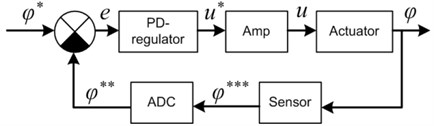
The following denotations are used in Fig. 2: $e$ – control error; $\dot{e}$ – first derivative of error.

The action of the regulator is described by the following Eq. (4):

4

$u^{*}=k_{p}e+k_d\dot{e},$

where $k_p$, $k_d$ are regulator coefficients:

5

$e={\phi }^{*}-{\phi }^{**},\text{is angle error},$

6

$\dot{e}={\dot{\phi }}^{*}-{\dot{\phi }}^{**},\text{is}\text{velocity}\text{error}.$

Proportional and PID regulators are widely used in mechatronic systems for providing position control systems [2-4], however PD-regulators are used in practice [9], which are considerably simpler to tune, including manual tuning methods [5, 11]. We note that the calculation of the integral component in the PID-regulator requires considerable computational power of the control system [5].

There are known methods of selection of optimal regulator coefficients based on analytical (formula) methods, as well as numerical methods of optimization of coefficients, such as built-in tools in Matlab/Simulink software packages. However, these methods can be used for non-linear systems, including systems with discrete elements in the negative feedback loop. In this work we propose a method of coefficient selection based on a numerical experiment.

3.2. Mathematical model of the discrete angle encoder

The value of the measured angle ${\phi }^{**}$ differs in quantization (${\phi }^{***}$) and time sampling from the real angle $\phi$ in the discrete system. We will now illustrate angle measurement using an angle movement (Fig. 3).

Fig. 3Graphical illustration of a discrete signal in the negative feedback channel of the control system: a) level-sampled signal (Δφ= 10°), b) time-sampled signal (f= 20 Hz) (1 – the sensor value of the angle φ***, 2 – real angular displacement of the link φ

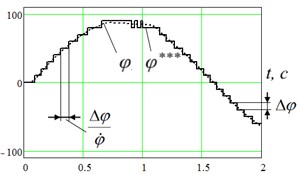
a)

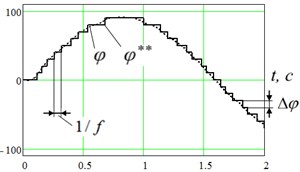
b)

It is clear from the graph that the value of the angle in the negative feedback of the mechatronic system is characterized by the sensor resolution $\mathrm{\Delta }\phi$, which is determined by the embodiment of the sensor (for example, a 7-bit digital encoder has a angle resolution 2,81°) and the features of the information system (for example, resolution of an analog-to-digital converter during sampling of the position potentiometer). Also, there is no time quantization with frequency $f$ due to transport delays in the system, speed of the measuring system, etc. We note that the combination of frequencies of the variation of the angle in the negative feedback channel due to level and time quantization acts a significant role during control. In this case we assume that $1/f\ll 1/\dot{\phi }$, i.e. the link moves with comparatively slower to the sample frequency of the sensor. In the studied model we model the discreteness of the sensor as follows:

7

${\phi }_i^{**}=\left\{\begin{array}{l}{\phi }_i-\mathrm{m}\mathrm{o}\mathrm{d}({\phi }_i,\mathrm{}\mathrm{\Delta }\phi )\mathrm{}\mathrm{}\mathrm{i}\mathrm{f}\mathrm{}\mathrm{}\mathrm{m}\mathrm{o}\mathrm{d}(t_i,\mathrm{}f)=0,\\ {\phi }_{i-1}^{**},\end{array}\right.$

here: $i$ – is the number of calculation step, $\mathrm{m}\mathrm{o}\mathrm{d}({\phi }_i,\mathrm{}\mathrm{\Delta }\phi )$ – the remainder of division ${\phi }_i$ by $\mathrm{\Delta }\phi$.

4. Organization of the numerical experiment and analysis of obtained results

The developed mathematical model allows us to define the parameters of the electromechanical system such as: values of mass, length of link and parameters of the control system’s speed.

A harmonic function is used as the reference signal (in order to reduce transition processes due to discontinuity of the reference function) and the period is taken to be equal to the duration of the modeling process. The angular velocity of the link is given as 2 rad/s:

where $A_0$ – is the amplitude of the oscillations, $\omega$ – is the angular velocity.

The choice of velocity is based on the requirements of the studied mechatronic system, which is the module of a lower-limb assistive exoskeleton [3]. The amplitude is given as 90° and defined as the maximum possible value based on the design features of the mechatronic system’s gear unit.

In order to analyze the control processes we introduce a vector of variable parameters: $\overrightarrow{b}={\left[k_p{k}_d\mathrm{\Delta }\phi f\right]}^T$. We define the ranges of variation of the studied parameters in this study as follows: (0.5$<k_p<$20),$$(0$<k_d<$1.5), (0.1°$<∆\phi <$20°), (5 Hz $<f<$100 Hz).

We obtain a region of parameters of the system, under which quality criteria of control will be minimum. There are many criteria for evaluating the quality of control, however many of them (static error, overshoot and oscillation) are applicable for step reference signal.

In this paper, as a quality dimensionless criterion, we offered the integral of the module error referred to the amplitude of the desired signal. It is one of the simplest and fully reflects the oscillatory movement of the link about a predetermined value criterion:

where $T_{max}$ is the time of modeling (as mentioned before, is determined by the period of the reference signal).

We show diagrams with the aim of defining the region of regulator parameters, for which oscillations in the system are either absent of minimal, as well as determining the case when the system is unstable.

For description of the results let us identify the following notation of areas of parameters characterizing the regulation quality: I – region with minimum integral error ${(e}_i<\text{2})$; II – region with negligible integral error ${(e}_i<\text{4})$; III – region with considerable error, oscillation is present ${(e}_i<\text{6})$; IV – region of instability ${(e}_i>\text{9})$;

Results of simulation are shown with the following parameters: $\overrightarrow{b}={\left[k_{p}01f\right]}^T$.

Fig. 4Values of integral errors ei for different frequencies of the automatic control system, f and coefficient, kp: a) frequency range: 5-26 Hz; b) frequency range: 20-100 Hz

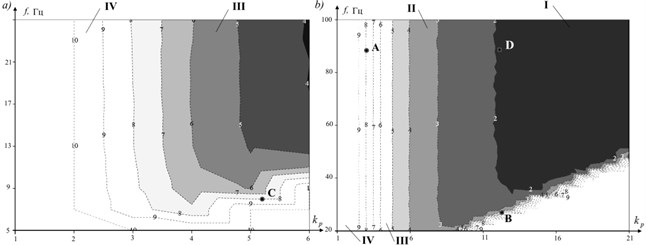
It can be seen from the diagram that the sensor’s sampling frequency has significant influence on the quality of control. The results show that there is a frequency region (Fig. 4, III-IV), in which an increase in the proportional coefficient leads to loss of stability of the system. The presence of these regions is explained by the inertial properties of the mechatronic system. A frequency region, in which an increase in the proportional coefficient does not lead to a reduction in the quality of control, is also visible on the diagram (Fig. 4, I). The given diagram enables us to tune the regulator parameters at given sample frequencies of the negative feedback sensor.

To illustrate the behavior of the system under different combinations of parameters, time-depended movement graphs and the desired signal are shown at Fig. 5.

Fig. 5Graphs of transient response at different points of the system parameters

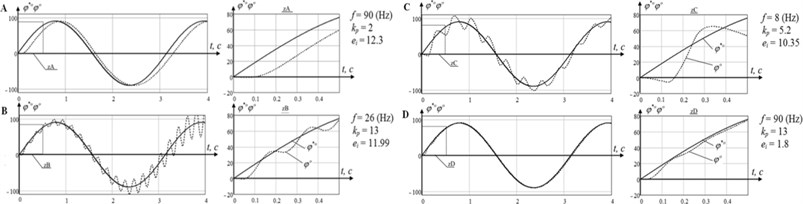
The graphs shown in Fig. 5 describe the transient response for various combinations of system parameters. At the point A, due to the small gain coefficient the phase error is observed, which leads to a sharp increase of the integral error that is noted on the charts. Oscillation and overshoot are absent.

At point B of the chart, there is an unstable mode with oscillations and increasing amplitude. At point C we get stable oscillations around the desired signal, the frequency and amplitude of these oscillations are determined by the properties of the system. Raising of coefficient $k_p$ increases amplitude and frequency both.

At point D we obtain good quality control, in which the oscillations present only at the beginning of the simulation due to discontinuity of a desired function.

Next, we consider the influence of the sensor resolution on the process of link movement with the following parameters $\overrightarrow{b}={\left[k_{p}0\mathrm{\Delta }\phi 50\right]}^T$.

The given diagram clearly shows that the reduction in the measurement accuracy due to discrete properties of the sensor leads to a decrease in the quality of control and even loss of stability; however, there is a region of values of the proportional component of the regulator, for which this effect is not so significant (see Fig. 6. I, II). We can also see from the diagram that the required quality of control cannot be achieved under any regulator settings for resolutions of the sensor greater than 7°.

Finally, we find different values of the gain coefficients with the following parameters $\overrightarrow{b}={\left[k_p{k}_{d}1\mathrm{}50\right]}^T$.

Fig. 6Values of integral error for different values of resolution of the sensor, Δφ and coefficient, kp

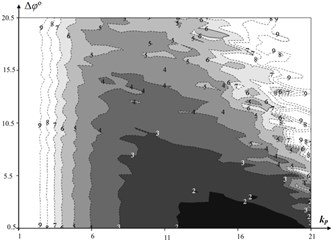
Fig. 7Values of integral error for different values of coefficients, kp and kd

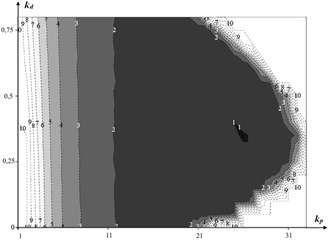
The diagram shown in Fig. 7 illustrates the region of regulator values under which the best quality of control with respect to absence of the oscillatory component and minimization of integral error is achieved. We note that instability of the system is achieved by varying both the proportional and differential component of the regulator due to the discrete character of the variation of the angle in the negative feedback loop.

5. Conclusion

This work presents a mathematical model that describes a mechatronic single-mass electromechanical system with electric drive, angle feedback and controlled by PD regulator. A special feature of this system is the consideration of the sensor discreteness in the negative feedback channel of the control system.

In this paper authors show that parameters such as the encoder resolution and the frequency of the automatic control system have a significant influence on the accuracy of controlled mechatronic system. We offered four areas of the system parameters for which different accuracy is achieved. The results showed that increasing the frequency and sensor resolution increases the quality of regulation. Due to discreteness in the feedback channel the controller parameters $k_p$ and $k_d$ have also a significant effect on control, but as well at a low resolution cannot achieve the required accuracy for small values of frequencies (comparable with the signal frequency and resolution). The minimum frequency and discreteness shown in the work, and can be used to tune up and design of mechatronic systems equipped with digital controllers and sensors.