Determining the vibration behavior of metal matrix composite used in aerospace industry by FEM

1. Introduction

Finite element method (FEM) is now a numerical method used effectively in solving complex engineering problems as accurate. The basic idea in the FEM, the problem is to find a solution by simplistic in a complex problem. Progress in the commercial Finite element analysis (FEA) software and in computing hardware has now made it practical to use advanced types as an everyday design tool of design engineers. In addition, competitive pressures and quality requirements demand a more in-depth understanding of product behavior under real life loading condition [1].

Solving complex mechanical problems increasingly demands the use of the finite elements method, which has, in recent years, become the key tool in structural design. The recent development of mechano-reliable couplings and stochastic or probabilistic finite element methods is a response to the limitations of deterministic numerical analysis. [2]. FEM can be applied in the materials' vibration behavior of a material can be determined [3].

The most important parameter in determining this behavior is detected natural frequency [5]. There is infinite natural frequency of each object in space. If, the natural frequency of an object is excited by a subdued function force. A lot of materials have been tested by plate or shell and these materials have been applied analytic solution as FEM [4].

The finite element analysis approach for vibration and acoustics has recently increased in the aerospace industry [5, 6]. Vibration behavior of materials and systems used in the aerospace industry in a very important and sensitive issue is of reference information [7, 8].

These works were presented to base on the mechanical theory, a finite element model for the aerospace was established and also the linear static structural analysis under particular conditions is performed to determine the modal stress and displacement distributions and the modal analysis is conducted to obtain the frequencies and their corresponding vibration shapes [9, 10].

Structure the behavior of the systems and materials are obtained by analyzing the simulating results, which are beneficial to the optimizing design for these vehicles.

In this paper investigate to AA2124/SiC/25p which is MMCs reinforced with particles and homogeneous distribution, which are used especially in the aerospace industry. Vibrations of the material was evaluated by the FEM analysis. The frequency modes of the MMCs were determined. In order to determine the reaction against the load material, the point has implemented and forced damped vibrations. Finally, the reaction spread by forced vibration damping materials was examined.

2. Experimental methods

The plates used in this study are AA2124-T4 alloy matrix MMC strengthened with 25 % SiC particles (AA2124/SiC/25p-T4). This material was supplied by Aerospace Metal Composite Limited (UK) in form of billet with size of 400×260×50 mm. The MMC material was produced by powder metallurgy and mechanical alloying techniques followed by hot forging and tempering to T4 condition (solution heating at about 505 °C for 1 h, quenching in 25 % polymer glycol solution and room temperature aging for >100 h). The ultimate tensile strength of the base AA2124/SiC/25p-T4 MMC is of 454 MPa. The chemical composition of the AA2124/SiC/25p-T4 MMC is shown in Table 1. MMC plates of 130×50×3 mm size were cut from this billet by electro-discharge machining technique. Mode of natural materials and 0-5000 Hz frequency range are determined.

The FEM analysis has been applied in the design in 2D and plate component is defined as “thin shell”. Component is designed as a 3 mm thickness. It is fixed by a plate. The material is homogenous. So it is defined as isotopically. The materials parameters such as Young’s modulus, Poisson’s and density is described by the product of information.

3. Results and discussion

In order to determine the natural frequency of vibration analysis it is necessary to determine the wavelength. the shortest wavelength to be created, according to the wavelength of the criteria can’t be less than the total size of 10 linear elements. Because, this study was the shortest wavelength in the elements used in a 2.5 mm size it should be determined as 25 mm. For these calculations, the wavelength and the angular frequency theory approach may be used as below in Eq. (1) and (2):

Other parameters as Modulus of elasticity ($E=$115 GPa), density ($\rho =$2880 kg/m³) Poisson ratio ($v=$0.3) should be defined after determination of the angular frequency and wavelength. Frequency range [–1.5000] as entered. The frequency is set to –1 to make sure that the initial calculation of the rigid body mode. Upgrading the size of the elements, which allow for the lower frequency modal analysis. AA2124/SiC/25p MMC has one natural frequency at 0-5000 Hz. The MMCs including 4092.23 Hz is only one natural frequency. Fig. 1 shows the response of the material with the force exerted on the material. There is obtained natural frequency.

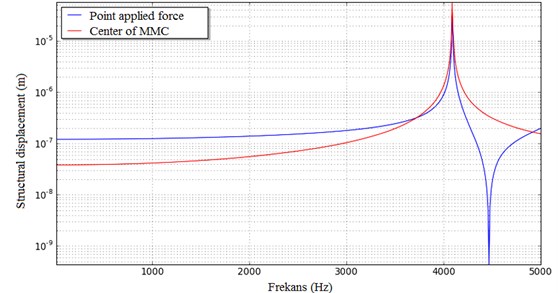
Point response to the forced damped vibrations of the material were investigated between 0 to 5000 Hz. After the analysis, material was examined against point loading of the frequency response function of the response and mapping.

Examining the graphic, it seen Fig. 2, The applied force was absorbed at 3900 Hz. the natural frequency of the material is 4092 Hz, it shows the point and below is safe operating for this MMC.

Fig. 1First modal shape of the plate

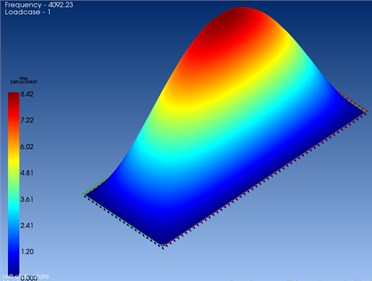
Fig. 2The displacement curves along the Z-axis

It can see at Fig. 3, MMC plate which is the natural frequency of 4092 Hz is observed reactions occur. It may be described as the force applied to the central point – the border region is seen decreasing order of a vibration transport.

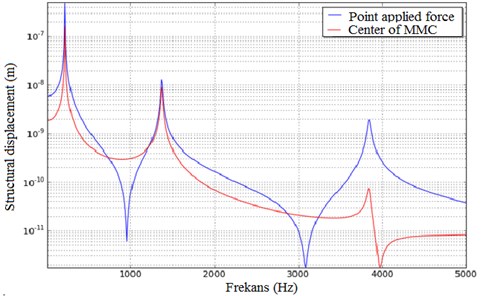
The MMC is forced damped vibration response of the spread was measured between 0-5000 Hz. One of the surfaces is defined as a condition of the boundary surface displacement. The other surface spread of forced damped vibration surface spread is defined as the installation of boundary conditions. Fig. 4 shows that the frequency response function of the response to the spread against loading and mapping.

Fig. 3The displacement occurs in the MMC at 4090 and 5000 Hz

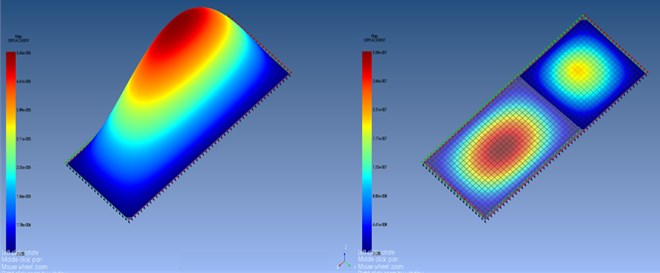
Fig. 5. illustrates reactions that occur in the center of the plate and the point force applied graphics. These reactions exhibit stable behavior occurs at the same frequency point.

Fig. 4The displacement curves in MMC

Fig. 5The displacement along the z-axis

4. Conclusions

The analysis of the MMC plates natural frequency and modal frequency of the material in this shape has been determined. The reaction among the materials was measured under node and distributed harmonic forces. natural frequency of the material was determinate as 4092 Hz. At this frequency point, materials can operate without resonance is observed. Also vibration modes of the material were determined. According to the analysis, the results are reliable secure frequency range from 0 to 500 Hz. Because the natural frequency of 4092 Hz material, the limit value is assessed as 5000 Hz. Up to this limit the modes frequencies was 220, 1380 and 3870 Hz, respectively. Material exhibits a fairly consistent behavior across vibrations and does not in different reference ranges.