The synthesis of four-bar mechanism

1. Introduction

In the teaching of subjects related to Machine Theory, supporting and complementing theoretical lectures with a simulation and analysis software, helps the students to understand deeply and visually the theoretical bases of the Mechanisms Science. The software has been developed focusing, not only on educational purposes but also on research in the field of computational kinematics and mechanism design applications [1]. The software presented in this article also has potential to be used by students of Master Degrees in Mechanical Engineering and other subjects related to Robotics, Mechanism Design, etc. GIM has been developed in a modular structure. After defining the kinematic structure of a linkage in the Geometry module, the user can perform the motion simulation in the Motion module. GIM is mainly oriented to the field of kinematic analysis, motion simulation and dimensional synthesis of planar mechanisms. In any case, it also includes other modules for workspace and singularity evaluation [2] and static analysis of mechanical structures. For example [3], at the solution of a problem of synthesis of directed and transmission gears of high classes it is necessary to use the kinematics equations for definition of a rotation angle $\theta$ of the plane if $Q$ it isn’t set in a case when the considered problem of synthesis of the opened ABCD four-bar chain [4]. Therefore, the vector method of the kinematic analysis is offered in this chapter which will be coordinated well with the method of synthesis of IKС stated in the previous chapter, and also it can independently be used for the solution of tasks on provisions, speeds and accelerations of the synthesizable mechanism [5-7].

2. Materials and methods

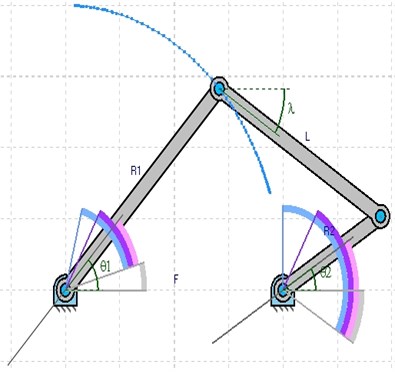
The equation of the coupler-point curve for a four-bar linkage may be obtained by analytic geometry. The derivation presented follows that of Samuel Roberts, with only slight changes in notation. The equation will be written in Cartesian coordinates, with the $x$ axis along the line of centers $O_A{O}_B$ and the $y$ axis perpendicular to that line at $O_A$ (Fig. 1). Let $(x\mathrm{\text{'}},y\mathrm{\text{'}})$, $(x\mathrm{\text{'}}\mathrm{\text{'}},y\mathrm{\text{'}}\mathrm{\text{'}})$, and $(x,y)$ be, respectively, the coordinates of points $A$, $B$, and coupler point $M$; then:

Since $A$ and $B$ describe circles (or arcs of circles) about centers $O_A$ and $O_B$, respectively:

Substituting the values of $x\mathrm{\text{'}}$, $y\mathrm{\text{'}}$ and $x\mathrm{\text{'}}$, $y\mathrm{\text{'}}$ into the last two equations yields and:

which, by application of trigonometric identities and ordering of terms, become:

Fig. 1Coordinate system and notations used to derive equation of coupler curve

The equation of the coupler-point curve may now be obtained by elimination of $\theta$ between the last two equations. Solving these equations for $\mathrm{c}\mathrm{o}\mathrm{s}\theta$ and $\mathrm{s}\mathrm{i}\mathrm{n}\theta$ and substituting the values obtained into the identity $\mathrm{c}\mathrm{o}{\mathrm{s}}^2\theta +\mathrm{s}\mathrm{i}{\mathrm{n}}^2\theta =1$ yields the general four-bar coupler-curve equation:

In this, $k$ is the constant of the sine law applied to the triangle $AMB$:

This equation is of the sixth degree and because of its properties also bears the formidable title of tricircular sextic. One of its properties has been mentioned: a straight line will intersect it in no more than six points. Its further features may be studied either geometrically or algebraically. The geometric examination begins. An introduction to the algebraic study of coupler curves will be given by considering some properties deduced by Roberts and others. As a guide to an understanding of the methods of analytic geometry, second-order curves (conic sections) will be examined on route. On setting:

Eq. (5) takes the form:

Note that the equation:

represents a circle passing through $O_A$ and $O_B$ (Fig. 1). For reasons that will appear later, this circle is called the circle of singular foci. A multiple point of a curve, as, for example, a cusp or a crunode, is a point where the curve has several tangents. We propose to show that the coupler curve has multiple points at each of it’s inter sections with the circle of foci. When a curve is defined by an equation of the form $F(x,y)=0$ its tangent may be found by equating to zero the differential of the function $F(x,y)$, $\partial F/\partial xdx+\partial F/\partial ydy=0$. In rectangular coordinates every equation of the form represents a circle:

Since $dx$ and $dy$ are infinitesimal changes in the coordinates $x$ and $y$ along the curve, they also define the slope of the tangent as:

At a multiple point, where the curve has several tangents, the above expression must be indeterminate, which means that both $\partial F/\partial x$ and $\partial F/\partial y$ must be zero to satisfy the indeterminancy. The left member of Eq. (8) is the function $F(x,y)$ corresponding to the coupler curve, whence:

A similar expression is formed for $\partial F/\partial y$ on replacing $x$ by $y$. Since the points of intersection of two curves are found by considering their equations as simultaneous, the intersection of the coupler curve and the circle of foci is given by the pair of equations:

Since the left member of the second equation is zero, each term of the first equation is likewise zero, and:

The last two quantities serve to make $\partial F/\partial x$and $\partial F/\partial y$zero also, thus satisfying the requirement of an indeterminate slope at the point of intersection of the two curves and establishing the presence of a multiple point. Examination of the curve Eq. (5) shows its terms of highest degree to be $x^6+y^6$. In consequence, the significant equation for points at infinity is $x^6+y^6=0$. As with the second-order curves, this equation is taken with $y=x/t$, giving:

as the equation, the directions of the points at infinity must satisfy.

This equation of the sixth degree has six solutions – all imaginary – and the coupler curve therefore has six imaginary points at infinity in the directions $t\mathrm{\text{'}}=i$ and $t\mathrm{\text{'}}\mathrm{\text{'}}=-i$.

each being a triple solution of Eq. (15). The cyclic points are therefore triple points of the coupler curve. The asymptotes, also imaginary, must be parallel to the directions $i$ and $-i$, and since each cyclic point is triple, there will be a total of six asymptotes forming two sets of three parallel imaginary lines. The determination of the asymptotes follows the method described for second-order curves. In order to carry out the computations more conveniently, Eq. (5) is first rewritten, use being made of the identity:

with $U$ and $V$ as the parentheses appearing in the left-hand member of Eq. (5). Thus, after some algebraic manipulations:

The substitution of $X$ for $x+iy$ and $Y$ for $x-iy$ in this equation yields is:

The highest powers of $X$ and $Y$ in this equation are $X^3$ and $Y^3$; the asymptotes are therefore obtained by equating their coefficients to zero. The coefficient of $X^3$ is:

The requirement that this coefficient be zero will be met if any one of the three equations:

is satisfied. When written in terms of Cartesian coordinates, these equations become:

They represent a set of three parallel asymptotes corresponding to the triple point at infinity in the direction $t\mathrm{\text{'}}=i$. (Parallel lines intersect at infinity.) Another set of three parallel asymptotes in the direction $t\mathrm{\text{'}}\mathrm{\text{'}}=-i$ is obtained by equating to zero the coefficient of $Y^3$ in Eq. (18), i.e.:

This requirement will be satisfied if one of the following equations holds:

These transformed into Cartesian coordinates are:

For a curve passing through the cyclic points-as the four-bar coupler curve does-the points of intersection of asymptotes of the curve in the direction of the cyclic points are called singular foci. Since the coupler curve has two sets of three parallel asymptotes of this type, it has a total of nine singular foci. Examination of Eqs. (21) and (24) shows that three of these intersections are real; i.e., there are three real singular foci. They are the origin $O_A$, the point $O_B$ ($x=b$, $y=$0), and a third point $O_C$ of coordinates:

which also lies on the circle of foci defined earlier in this section. It may be further observed that the angles at $O_A$, $O_B$, and $O_C$ of the triangle $O_A{O}_B{O}_C$ are respectively equal to the angles at $A$, $B$, and $M$ of the triangle $ABM$: the triangles $O_A{O}_B{O}_C$ and $ABM$ are therefore similar.

3. Results and discussion

A proper the synthesis of four-bar coupler-point curves has been developed within GIM software to provide information on the feasibility of the proposed design solution. Simulation tests have been carried out and results are discussed for validating the proposed design and characterizing its operation.

Fig. 2Computed plot of 3 postures and moving

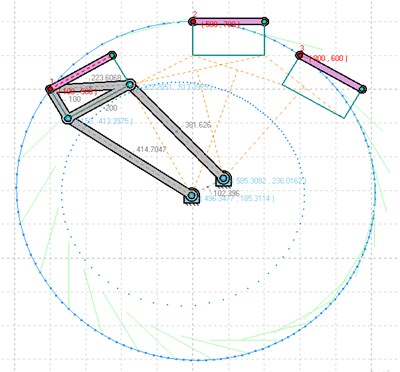
Fig. 3Computed plot of 3 postures and fixed

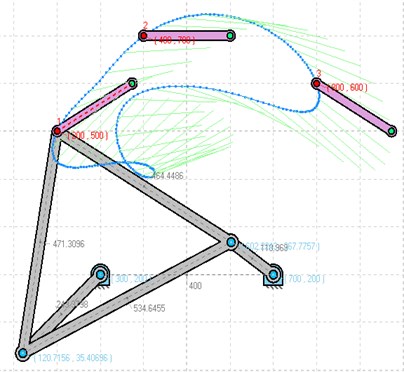
Fig. 4Computed plot of 4 postures

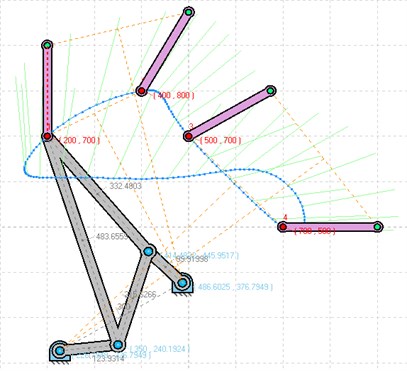
Fig. 5Computed plot of function generation

4. Conclusions

The software presented in this paper allows students and researchers to model and analyses in a quick and simple way n-DOF planar linkages. Using the software capabilities, the user is able to carry out a deep kinematic performance analysis of the whole mechanism. GIM software has proven to be a very effective tool to complement and reinforce the theoretical concepts explained during the lectures of subject related to Mechanism and Machine Science.