Abstract
Shear lag effect of curved box girder under multi-dimensional seismic excitation is studied in this paper. Firstly, spatial finite element model is established based on ANSYS, and a seismic wave, which is recorded in second site, is chosen as ground acceleration time history. Secondly, elastic dynamic time-history analysis focused on shear lag effect is carried out, where 4 working conditions, 3-D seismic, longitudinal-vertical seismic, vertical seismic and transverse seismic only, are considered. Thirdly, critical angle of seismic waves is investigated, it is seen that under seismic excitation, there is a prominent shear lag effect on upper flange at mid-span of the curved box girder, and there are also various shear lag effect modes under the different working conditions of seismic excitation. The shear lag under 3-D seismic is severest, normal stress is concentrated on inside upper flange, then that under longitudinal-vertical seismic is less serious, in which case, the stress is appearing within a regional proximity to the junction between webs and flange, the next is under vertical seismic, and the shear lag effect under transverse seismic is most non-prominent. Finally, the numeric results are compared with the experimental results from a vibration table testing, which shows great consistencies.
1. Introduction
In bridge construction, thin-walled box girder is a common structure type, the shear lag effect [1] caused by non-uniform shear deformation along transverse direction is the main reason for the accidents of some major projects. It was indicated by many researchers that shear lag will not only cause local stress concentration and cracks [2] but also impairs the bending stiffness of the beam, which leads to the increasing of vertical deflection [3] and affects the safety and durability of bridges. At present, there is good solution for shear lag effects under static loads. Except for the action of dead load, bridges will bear vehicle load, wind load, and sometimes seismic action, therefore it is necessary to study shear lag of box girder under dynamic loads. In the paper, spatial shell finite element model is setup to study shear lag of curved box girder and search for the critical angle of seismic waves with elastic time-history analysis method.
2. Finite element model
The material properties and structural dimensions of curved box girder are shown in the literature [4], in this paper, some dimensions are different, shown as Fig. 1, mass density 1180 Kg/m3, structural parameters: 8 mm, 100 mm, 150 mm, 120 mm, curvature radius 2 m, curvature angle 60°. The material parameters are as following: Young’s modulus 3000 MPa, Poisson’s ratio 0.385.
In the paper, 3D finite element method using 4-nodes shell elements is adopted in the setup of the finite element model of the curved box girder. The finite element model of curved box girder is shown as Fig. 2, there are 800 elements and 820 nodes, as for the boundary conditions, , , and , are restricted at the junction between web and bottom flange in one side, while , and are restricted in the other side.
Fig. 1Cross section
Fig. 2Finite element model

3. Dynamic time-history analysis
Seismic wave (north-south component), which is recorded in second site, is chosen as seismic excitation in the paper, the peak value and acceleration are revised by basic earthquake protection intensity shown as Eq. (1) and Fig. 3:
where is the acceleration of original seismic wave at time , is the corresponding peak value, is the revised acceleration, and is the maximum ground horizontal acceleration.
Fig. 3EI Centro seismic wave
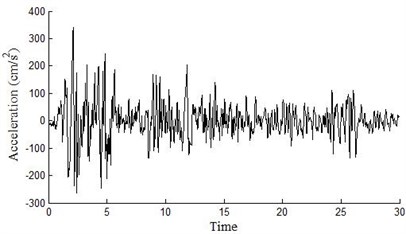
a) Original wave
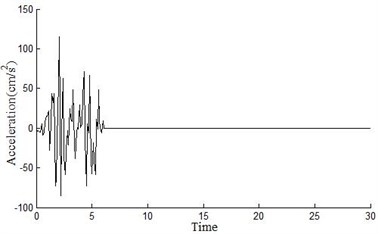
b) Revised wave
As is discussed above, the shear lag effect of curved box girder under multi-dimensional seismic excitation and the influence of 4 vibration working conditions on shear lag are investigated in detail. Considering the main reasons of shear lag are vertical bending deformation and plane shear deformation, the peak acceleration in different directions are set up as 1 (horizontal direction1), 0.85 (horizontal direction 2) and 0.65 (vertical direction) [5], the working conditions are shown in Table 1.
Table 1Working conditions of seismic excitation
Seismic excitation | EL Centro Seismic wave | |||||
Working conditions | I | II | III | IV | ||
Direction | Crest factor | 1 | – | – | 0.85 | |
– | – | 1 | 1 | |||
– | 1 | 0.65 | 0.65 | |||
Seismic types | One-way | One-way | Two-way | Three-way | ||
According to D’Alembert principle, vibration equation of the structure is shown as following:
Considering multi-dimensional seismic excitation, the vibration equation can be got:
where , and are the mass matrix, damp matrix and stiffness matrix respectively, is the seismic mass matrix, is the ground acceleration.
Newmark- method or Wilson- method are adopt for the analysis and the displacement response of structure can be obtained.
The shear lag coefficient is shown as Eq. (4) [1]:
where is the real stress value, is the stress calculated by primary beam theory.
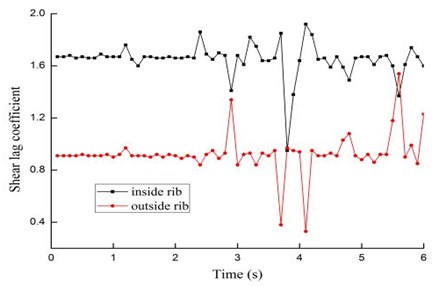
Because of shear lag effect, the stress peak is at the junction between upper flange and web, the response of shear lag coefficient at mid-span cross section is shown as Fig. 4. It can be seen that there is a fluctuation of shear lag coefficients around a certain value at most of time, but the fluctuation is small, the reason for this is the ground acceleration is different at each time and the stress is not equal to each other even though the shear lag coefficients are the same. Therefore, the average shear lag coefficients can be acquired through deleting a few large-variation values.
Fig. 4Response of shear lag coefficients under 3-D seismic excitation
4. Shear lag effect
According to the analysis above, the shear lag coefficients of upper flange under 4 working conditions are shown in Fig. 5.
In Fig. 5, it can be seen that there is a prominent shear lag effect under 4 working conditions of seismic excitation, and there are various shear lag effect modes under different working conditions of seismic excitation. As known to all, the transverse stiffness of box girder is greater than the torsion stiffness, the vertical bending stiffness is minimum, therefore, in Fig. 5(a), the transverse bending deformation and distortion is small when under the transverse seismic excitation alone, while shear lag effect is prominent when under the 3-D seismic excitation, which indicates that shear lag is caused by the vertical bending deformation and plane shear deformation. Just like Fig. 5(b) shows, the shear lag coefficients reach their peak at the ribs and decrease along two sides.
A quantitative analysis is performed to study the influence of working conditions on shear lag effect, non-uniformed coefficient of stress is defined as Eq. (5) and the results are shown as Table 2.
where is non-uniformed coefficient; is shear lag coefficient.
Fig. 5Shear lag effect under different seismic excitations
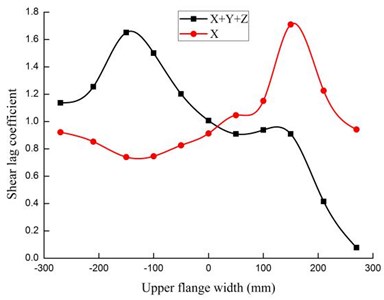
a) and
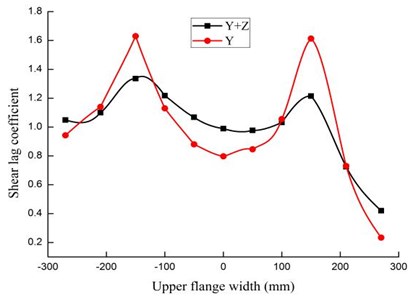
b) and
Table 2Non-uniformed coefficients of stress (%)
Nodes number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
– | – | – | – | – | – | 1.6 | 14.4 | 72.8 | 23 | – | |
– | 14 | 63 | 13 | – | – | – | 5.5 | 61.3 | – | – | |
4.9 | 9.6 | 30 | 22.6 | 5.4 | – | – | 1.9 | 23.2 | – | – | |
14.1 | 25.7 | 66.2 | 53 | 18.8 | 1.5 | – | – | – | – | – | |
Notes: node number is from inside to outside of curved box girder, “–” is negative shear lag and not considered | |||||||||||
It can be seen clearly from Table 3 that shear lag is severest under 3-dimensional seismic, normal stress is concentrated on inside upper flange and the structure is easily damaged, longitudinal-vertical seismic is the next, and vertical seismic is the least, where the stress is appearing within a regional proximity to the junction between webs and flange. The shear lag is the most non-prominent under transverse seismic excitation.
Fig. 6Comparison of experiment and numeric results
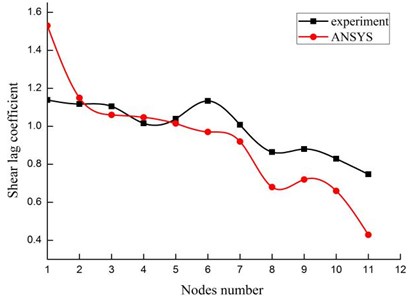
In order to verify the validity and reliability of finite element model, a cantilever box girder model is founded with the same method to compare the results acquired with the shaking table testing [6], the material properties and cross-section dimensions are the same with each other, the numerical analysis of ANSYS agrees well with that of experiment shown as Fig. 6, the relative error is a bit big at several measuring points, the reason for this is that the composite effect of damp, stiffness and mass is not considered in the finite element model, while the error is small at most of measuring points.
5. Conclusions
The following conclusions are acquired:
1) There is a prominent shear lag effect in the single-box single-cell simply supported curved box girder at upper flange under seismic excitation, and there are great differences in the shear lag modes under the different working conditions.
2) The shear lag is most prominent under 3-D seismic excitations, the next is longitudinal-vertical seismic, then followed by vertical seismic, and the shear lag under transverse seismic is most non-prominent.
3) Full attentions should be paid to the critical angle of multi-dimensional seismic excitation when shear lag effect of curved box girder under seismic excitation is analyzed.
References
-
Xiang Haifan, Fan Lichu Advanced Theory of Bridge Structures. Second Edition, China Communication Press, Beijing, 2008, (in Chinese).
-
Sun Lu, Wang Wenlei, Wu Guoqi, Li Yaoxiong Analyses of the causes for crack on the end side of box girder for railway passenger dedicated line and its construction control. Journal of Railway Engineering Society, Vol. 10, 2007, p. 46-51., (in Chinese).
-
Zhang Yuanhai, Li Lin, Lin Lixia, Sun Xuexian Beam-segment finite element analysis on shear lag effect of thin-walled box girder adopting additional deflection as generalized displacement. China Civil Engineering Journal, Vol. 46, Issue 10, 2013, p. 100-107, (in Chinese).
-
Lu Hailin Theoretical Analysis and Experimental Study on Shear-Lag Effect of Prestress Concrete Curved Box Beam. Tianjin University, Tianjin, 2007, (in Chinese).
-
Zhou Yin, Lv Xilin Method and Technology for Shaking Table Model Test of Building Structures. Science Press, Beijing, 2012, (in Chinese).
-
Lu H. L., Peng T. F., Huang M. S., Zhu S. B. Experimental study on shear lag of curved box girder under earthquake excitation. Vibroengineering Procedia, Vol. 5, 2015, p. 417-422.
