Abstract
The design of key parts of civil engineering structures often undergo several modifications to ensure that the usability of entire structure meets the requirements. Dynamic characteristics are important parameters to evaluate the performance of structure, so it is necessary to calculate dynamic characteristics after each modification. This paper proposes a new method to calculate the dynamic characteristics of the structures rapidly after each modification. According to this method, the structure is decomposed into relatively simple substructures, and the dynamic characteristics of the whole structure can be obtained by the modal synthesis method (MSM). When a substructure has been modified, its dynamic characteristics can be calculated by using the matrix perturbation method (MPM). The proposed method is applied to the numerical calculation of a -shape continuous beam bridge, and the results show that the method is correct and efficient.
1. Introduction
Dynamic characteristic is an importantly controllable parameter in civil engineering structure design, especially for those structures which have the requirements of seismic performance. In general, the design of any structures experienced many modifications before final shape. Dynamic characteristics need to be calculated after each modification to known whether they can meet the requirements for structural performance. Thus, it is necessary to calculate the structural dynamic characteristics rapidly after each modification for improving the design efficiency.
Analytical, semi analytical and numerical methods are often used to calculate the structural dynamic characteristics. He et al. developed an analytical approach to simulate the coupled vibration of bridges and running vehicles, and to investigate the dynamic characteristics of rationalized curved bridges [1]. Chen et al. developed a coupling vibration model of vehicle-bridge system by Euler-Bernoulli beam theory [2]. Azrar et al. presented a semi-analytical approach to the non-linear dynamic response of beams based on multimode analysis [3]. And they also used the method to the large amplitude forced vibrations of beams [4]. Laura et al. studied free vibrations of Bernoulli beams of bilinearly varying thickness using the optimized Rayleigh-Ritz method, the differential quadrature technique and the finite element approach [5]. Datta and Sil obtained the solution for natural frequencies graphically because of implicitness of the parameter in the equation which contains a carious kinds of Bessel functions of different orders for a cantilever beams of constant width and linearly varying depth [6].
From above literatures analysis, the finite element method (FEM) maybe a common technique for dynamic properties analysis of civil engineering structures. However, the determinate orders of eigen equations will increase with the improvement of computational accuracy. Obviously, it must be a waste of time to use FEM to calculate the dynamic characteristics after each modification for civil engineering structure. MPM is an effective method to analyze the structural dynamic characteristics after slight modifications [7, 8]. Compared with the traditional FEM, it will certainly improve the analysis efficiency in the process of structural modification. However, the modification usually aimed at the key parts of civil engineering structures but not for the whole. It is obviously inappropriate to calculate the dynamic characteristics of the whole structure by using MPM. The basic idea of MSP is to divide the complex structure into several substructures, and the dynamic characteristics of the whole structure are obtained through the coordination conditions of substructures. The dual coordinate free-interface method of mode synthesis has a high precision [9].
In order to improve the computational efficiency of dynamic characteristics in the design of civil engineering structures, this paper presents a method to calculate the structural dynamic characteristics quickly after each modification. Firstly, the structure is decomposed into relatively simple substructures, and the dynamic characteristics of the whole structure can be obtained by MSM. Then, when a substructure has been modified, its dynamic characteristics can be calculated by using the matrix perturbation method (MPM).
2. Double coordinate free-interface method of mode synthesis
The precision and astringency of double coordinate free-interface method of mode synthesis are greatly improved due to the introduction of residual attachment mode. At the same time, due to introduction of low-order matrix of dynamic characteristic equation makes the solution quite easy. As a result, this method is often used to analyze the dynamic characteristics of large structures. The analysis process is as follows [9]:
(1) The stiffness matrix and mass matrix for all uncoupled substructures are:
where is the total mass matrix, is the total stiffness matrix, is the mass matrix of the th substructure and is the stiffness matrix of the th substructure.
Then free-interface keeping modes and residual attachment modes are calculated and the coordinate transformation for the first time is conducted:
where is displacement matrix, is the keeping normal mode and is the mode displacement matrix, which can be expressed as:
where is the displacement of th substructure, is the free-interface keeping normal modes of th substructure and is the mode displacement of th substructure.
(3) can be divided into independent generalized coordinates and non-independent of the generalized coordinates, and the transformation is:
where is the location matrix and is the mode displacement after transformation.
Based on interface conditions (including displacement equality and internal force balance), the coordinate transformation for the second time is conducted i.e.:
where is the transformation matrix for the second time, is is the system independent generalized coordinate. By substituting Eq. (7) into Eq. (6) we can draw:
Thus the mass matrix and stiffness matrix integrated can be obtained:
Substituting Eqs. (9-10) into structural vibration equation, the free vibration equation can be written as:
The system eigenvalue can be calculated according to Eq. (11) and the system eigenvector can be expressed as:
3. Matrix perturbation method
The structural first-order perturbation solution is [10]:
where and are the first-order perturbation of the th order eigenvalue and eigenvector after structural parameters modified, respectively. and are the th order eigenvalue and eigenvector for the original structure, respectively; and are the increments of mass matrix and stiffness matrix after structural parameters modified, respectively; is the mass matrix before perturbation.
The structural second-order perturbation solution is:
where and are the second-order perturbation of the th order eigenvalue and eigenvector after structural parameters modified, respectively. So, the mode shape and frequency of structure after small parameter modified are:
The existed researches indicate that the results obtained by the first-order perturbation are satisfactory when the change of structural parameters is less than 15 %, while the change of structure parameter is 15 %-30 %, the results obtained by the second-order perturbation are suitable and satisfactory.
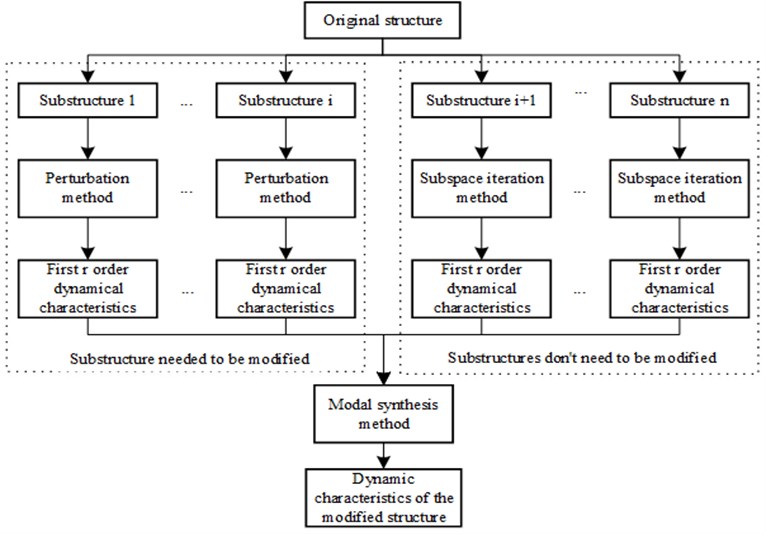
4. The process of solving dynamic characteristics by combining MSM and MPM
Structures often need to be modified for optimal design. In order to improve efficiency of calculation, the analysis method combining MSM and MPM is proposed. The basic idea of this method is as follows: firstly, original structure is divided into several simple substructures to solve the dynamic characteristics, in which the modified parts need to be separated alone particularly. When some parts of the structure are modified, only the corresponding substructures need to be reanalyzed; finally, the dynamic characteristics of the whole structure can be obtained by MSM.
Fig. 1The general process of dynamic characteristics analysis method based on the combination of the MSM and MPM
5. Example
Fig. 2 shows the common -shape box girder bridge, in which the red part is a section with variable width and length 30 m and the others are uniform. The spans of main line bridge are 4×20 m and the bifurcation possesses two spans of 11.5 m and 23.5 m. The Young’s elastic of upper structure is 3.25×1010 N/m2, density is 2500 kg/m3, Poisson’s ratio is 0.2.
The section with variable width section needs to be modified many times, which is changed from the original straight line to the final parabola. And Fig. 3 draws only third and fifth intermediate process of change. The section with variable width is separated into an independent substructure, and the integral structure is decomposed as shown in Fig. 2. After each modification, the dynamic characteristics of substructure 2 can be obtained by MPM. The substructures 1, 3 and 4 have not been changed, and their dynamic characteristics don’t need to be recalculated. Finally, the low order dynamic characteristics of the whole structure can be obtained quickly by MSM.
The first three frequencies of the structure calculated are shown in Table 1. It can be seen that the results calculated by combination of MSM and MPM and FEM are very close.
Fig. 2Schematic diagram of model

Fig. 3Process of gradual modification for substructure 2
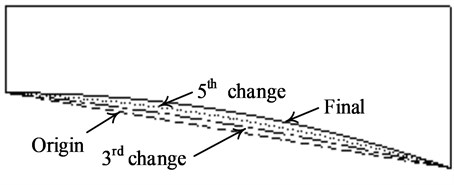
Table 1Results calculated by MSM and MPM compared with FEM
Mode | 1 (Hz) | 2 (Hz) | 3 (Hz) | |
Origin | MSM and MPM | 6.149 | 6.935 | 7.859 |
FEM | 6.150 | 6.936 | 7.861 | |
Error (%) | 0.02 | 0.02 | 0.02 | |
3th change | MSM and MPM | 6.127 | 6.910 | 7.832 |
FEM | 6.129 | 6.912 | 7.834 | |
Error (%) | 0.02 | 0.03 | 0.02 | |
5th change | MSM and MPM | 6.106 | 6.886 | 7.805 |
FEM | 6.107 | 6.888 | 7.806 | |
Error (%) | 0.03 | 0.03 | 0.02 | |
Final | MSM and MPM | 6.084 | 6.862 | 7.778 |
FEM | 6.086 | 6.864 | 7.779 | |
Error (%) | 0.03 | 0.03 | 0.02 |
6. Conclusions
In order to improve the computational efficiency of dynamic characteristics in the design of civil engineering structures, this paper presents a method to calculate the structural dynamic characteristics rapidly after each modification by combining the MSM and MPM. The proposed method is applied to the numerical calculation of a -shape continuous beam bridge, and the results show that this method is not only accurate but also efficient. It can be used as an alternative and efficient tool for the solution to those civil engineering structures which need to be modified many times.
References
-
He X., Noda Y., Hayashikawa T., et al. An analytical approach to coupled vibration of curved rationalized girder bridges and running vehicles. Procedia Engineering, Vol. 14, 2011, p. 2906-2915.
-
Chen Y., Huang X. Q., Ma Y. F. Coupling vibration of vehicle-bridge system. Applied Mathematics and Mechanics, Vol. 25, Issue 4, 2004, p. 390-395.
-
Azrar L., Benamar R., White R. G. Semi-analytical approach to the non-linear dynamic response problem of s-s and c-c beams at large vibration amplitudes part I: General theory and application to the single mode approach to free and forced vibration analysis. Journal of Sound and Vibration, Vol. 224, Issue 2, 1999, p. 183-207.
-
Azrar L; Benamar R., White R. G. A semi-analytical approach to the non-linear dynamic response problem of beams at large vibration amplitudes, part II: Multimode approach to the steady state forced periodic response. Journal of Sound and Vibration, Vol. 255, Issue 1, 2002, p. 1-41.
-
Laura P. A. A., Gutierrez R. H., Rossi R. E. Free vibrations of beams of bilinearly varying thickness. Ocean Engineering, Vol. 23, Issue 1, 1996, p. 1-6.
-
Datta A. K., Sil S. N. An analysis of free undamped vibration of beams of varying cross-section. Computers and Structures, Vol. 59, Issue 3, 1996, p. 479-483.
-
Fox R. L., Kapoor M. P. Rates of change of eigenvalues and eigenvectors. AIAA Journal, Vol. 6, Issue 12, 2015, p. 2426-2429.
-
Rogers L. C. Derivatives of eigenvalues and eigenvectors. AIAA Journal, Vol. 8, Issue 5, 1970, p. 943-944.
-
Craig R., Chang C. J. Free-interface methods of substructure coupling for dynamic analysis. AIAA Journal, Vol. 14, Issue 11, 1976, p. 1633-1635.
-
Chen S. H., Guo R., Meng G. W. Second-order sensitivity of eigenpairs in multiple parameter structures. Applied Mathematics and Mechanics, Vol. 30, Issue 12, 2009, p. 1475-1487.
About this article
This work was funded by the National Natural Science Foundation of China (Grant Number 51478203), Training Program for Outstanding Young Teachers of Jilin University.
