Research on vibration and acoustic radiation properties of planetary reducer box

1. Introduction

Reduction gearing device is one of the key equipment of naval vessel power system, the propeller could obtain reasonable speed to improve the efficiency of propulsion through it, also the optimal layout of various combined propulsion schemes and their propulsion device is realized by the Reduction gearing system [1]. Therefore, the optimization design of the structural and material of the reducer box is especially necessary for the vibration and acoustic radiation properties of the whole structure [2, 3].

Mature analysis methods for the noise prediction of the box structure at present mainly has the boundary element method (BEM) [4, 5], the statistical energy method [6-9] and so on. For the properties of broad boundary adaptability, accurate prediction of low frequency and high computational efficiency, the boundary element method is widely used by engineers and technicians. As for the statistical energy method, the modal density problem of its subsystem makes the method limited to medium and high frequency noise prediction. Zhao Beilei and others, starting from the basic principles of the statistical energy method, is studied the influence of the internal excitation, such as time-varying mesh stiffness and gear error on the gearbox radiation noise [10]. Litvin et al. studied the vibration and acoustic radiation properties during the working process of the box structure through experiment [11]. On the one hand, under the condition of stress, the box structure can transform the excitation into excitation or noise source, which has influence on the internal box structure through the force transmission chain. On the other hand, the internal load can cause the entire box structure excitation or noise source through passing to the external connection structure of box.

After a lot of paper-researching about box structure noise prediction, it is not difficult to find out that the vibration noise of the box structure is mainly through the experiment to diagnose the operation noise fault. However, the general vibration noise diagnosis analysis is not conducive due to the non-replicability of the experiment and the high cost. For this reason, combined with the FEM/BEM hybrid method, this paper establishes the gearbox noise properties analysis model of this type of box structures in the preliminary design stage.

2. Establishment of the analysis model

2.1. Geometric model

As the marine planetary reducer box usually works under the full frequency, this paper studied the vibration noise properties of the planetary reducer box under the full frequency in combination with the practical condition of box structure, combined the finite element and the boundary element method. On the basis of knowing the calculation method, the physical model of the structure is established by Pro/E software according to the design drawings. The radial length of the box is 1.20 m, the circumferential diameter is 1.22 m, the thickness of the box is 6 mm, the thickness of the end plate is 10 mm, the thickness of the strengthening rib plate is 6 mm, the box material is steel, the outer wall is decorated the strengthening rib to increase the strength of the box. The main material parameters: elastic modulus $E=$2.1 MPa, Poisson ratio $\mu =$ 0.3, the density $\rho =$7800 kg/m³, and the structural damping is 0.2 %.

Some tiny parts and irregular curved surface should be considered when meshing the model of planetary reducer box. As the planetary reducer box has complex structure, the thickness is different, and the chamfer and excessive fillet and bolt holes are also different, so some unnecessary geometric characteristics should be removed under the premise that does not affect the calculation accuracy. The original geometric model and after geometric processing of the box is shown in Fig. 1.

Fig. 1Geometric model of the box

a) The original geometric model

b) The box modal after geometric processing

2.2. Establishment of the FEM and BEM analysis model

Meshing the model in Hypermesh after establishing the geometric model, then import it into the finite element software ABAQUS, which is based on finite element method, to build the finite element vibration characteristic analysis model. After that, import the finite element analysis model into VA-one software, which is based on boundary element method, to establish the BEM noise properties analysis model. There are totally 515 FE subsystems in the whole box structure model, which are actually accepting and transmitting energy. They are all plate and shell subsystems, as shown in Fig. 2.

Fig. 2The FEM and BEM analysis model of the reducer box

a) Finite element mesh model

b) Finite element analysis model

c) Boundary element analysis model

3. Acoustic radiation properties analysis of the box

To analyze the acoustic radiation properties of the box, a BEM Fluid is set up 5 m away from the box, and the surrounding flow field of the box was set to air. After that, a Generate Cube Recovery Date Mesh is established 1 m outside the structural pavement to collect the radiation noise generated at 1m away from the box. Finally, ten Sensors are arranged on each inner surface of the cube to collect the sound pressure generated by each part of the box at that point. And the BEM Fluid and the boundary element mesh of the subsystem are connected manually, as shown in Fig. 3.

Fig. 3Boundary element calculation mode of the box and BEM Fluid subsystem

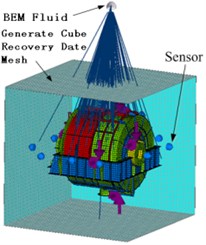
Fig. 4Acoustic radiation pattern of each part of the box under typical excitation

a) Acoustic radiation pattern of front end plate under typical excitation

b) Acoustic radiation pattern of under box under typical excitation

c) Acoustic radiation pattern of upper box under typical excitation

d) Acoustic radiation pattern of back end plate under typical excitation

Considering the actual situation of the box structure, the equivalent loss factor is 0.002. In order to compare the radiation noise produced by each part of the structure conveniently, as well as taking the characteristics of each part of the box into account, the whole box is divided into four parts: front end plate, upper box, under box and back end plate. In order to correctly analyze the acoustic radiation properties of the box, noise prediction was carried out on the box without consideration of the acoustic protection. And the proportion of the radiation noise in the total noise is analyzed so as to provide theoretical support for box noise reduction optimization.

The sound pressure cloud of each part of box structure under typical excitation is shown in Fig. 4. Then extract each measuring point’ sound pressure value to obtain the comparison of the sound pressure levels of different parts under different frequencies, as shown in Fig. 5.

From Fig. 4 and Fig. 5 we can get the conclusion that the radiation sound pressure value of the front end plate and the upper box is relatively large in the low frequency range (before 200 Hz); while in the middle and high frequency range (after 200 Hz), the radiation sound pressure value of the back end plate and the under box is gradually increased, more than the front end plate and the upper box. Collect the sound pressure level of each measuring point, and calculated the total sound pressure level of each part of the box, as shown in Fig. 6.

Fig. 5Contrast curves of each part’ sound pressure levels of the box under different frequencies

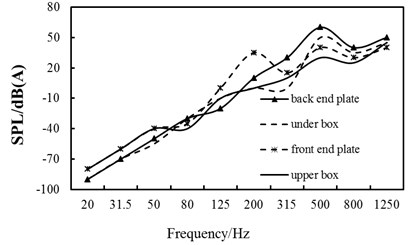
Fig. 6The total sound pressure level of each part of the box

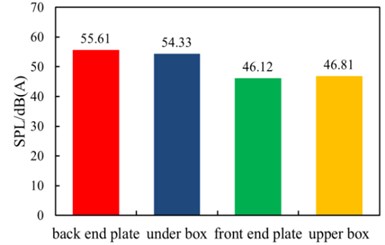
Fig. 6 shows that the total contribution of the radiation noise of each part of the box is: back end plate > under box > upper box > front end plate. It can be seen that the radiation sound pressure of the back end plate and the under box is relatively large before the acoustic processing is not made to the box structure, which is the dominant component of noise. Therefore, it needs to be paid attention to while vibration and noise reduction.

In order to improve the sound radiation characteristics of the box and reduce its vibration noise, acoustic protection means can be used to noise reduction processing. First laying damping layer on the outer wall of the box, and then using the sound insulation layer to fix outside the damping layer, finally laying sound absorption layer outside the sound insulation layer. When Constrained damping structure is subjected to bending deformation, it will force a relatively soft damping layer not only occurs tensile-compression deformation, but also shear deformation, which will dissipate more vibration energy, so the purpose of noise reduction processing can be achieved. The main change of the dynamic characteristic is the change of the structural loss factor after laying constrained damping structure, so the main means of vibration and noise reduction is to improve the compound loss factor of the box structure when the structure is determined.

After the acoustic protection treatment, the equivalent loss factor of the constrained damping structure in the calculated frequency band is 0.011, and contrast curves of each part’ sound pressure levels of the box under different frequencies are shown in Fig. 7. It can be seen from Fig. 7 that the radiation sound pressure value of the front end plate and the upper box is relatively large in the low frequency range; while in the middle and high frequency range, the radiation sound pressure value of the back end plate and the under box is gradually increased, more than the front end plate and the upper box. At the same time, it can be seen that the radiation noise of box structure increases with the increase of frequency, which is approximately the same as the radiation noise of the box structure before acoustic protection. The total sound pressure level of each part of box after acoustic protection are shown in Fig. 8.

Fig. 7Contrast curves of each part’ sound pressure levels of the box under different frequencies after acoustic protection

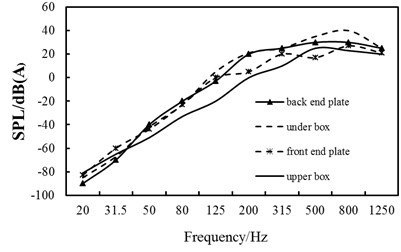
Fig. 8The total sound pressure level of each part of the box after acoustic protection

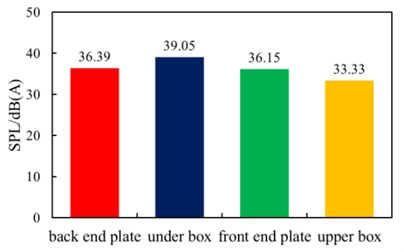
Fig. 8 shows that the total sound pressure level of the under box is larger than the total sound pressure level of the back end plate, which becomes the dominant component of noise. Before and after acoustic protection, the total radiation sound pressure level can be reduced more than 5 dB, which can meet the requirements of the vibration and noise reduction design. From the above analysis, the sound pressure level of box is decreased with the increment of its structural loss factor. Therefore, we should try to increase its structure loss factor, with the feasibility and economic conditions permitting, in order to get the best effect of optimization.

4. Conclusions

Based on FEM/BEM method, the analysis model of vibration and acoustic radiation properties of planetary reducer box is established in this paper, and the vibration and acoustic radiation properties of planetary reducer box is analyzed. First of all, the finite element analysis model is established in ABAQUS. Secondly, the acoustic radiation boundary element model is built through the VA-one, then calculate the sound pressure distribution of the surface and sound field of the box, and field contribution degree of radiation noise of the box is also calculated. And the influence law of the main structural parameters on radiation noise properties is studied. On this basis, the noise reduction optimization measures of box are preliminarily studied and the results are compared in this paper, which can provide technical support for the structural scheme design of planetary reducer box.