Abstract
Previous studies have attempted to identify weak links in the dynamic characteristics of the planetary gear reducer (PGR) exterior body structure (EBS). Through numerical simulation, these studies analyzed the modals and natural frequencies and the vibration types of each order of the EBS. However, these scholars have never focused on the main factors affecting the dynamic characteristics of the EBS of this subject. This study in the topic has analyzed the vibroacoustic characteristics of an EBS and optimized its design using numerical simulation. Herein, the contribution of the vibration transfer path from the excitation points on the exterior body to the machine foot is emphatically revealed, and the influences of the main structural parameters on the transfer characteristics are discussed. An optimal EBS for a PGR with lower acoustic vibrations is designed in detail, and a composite EBS with damping vibration attenuation and acoustic absorption is proposed. The radiation acoustic characteristics without acoustic protection and damping materials are analyzed. These research results are implemented in order to realize the dynamic characteristics, transmission, and radiation acoustic characteristics as objects of optimization, and the structural design parameters of the PGR exterior body are deeply optimized using dynamic modification and sensitivity analysis. This topic focuses on the vibroacoustic coupling of EBS in stationary fluid and average flow field, based on the analysis method of theoretical modeling and numerical calculation, the EBS dynamic response and vibroacoustic characteristics under the action of frontal excitation external acoustic flow field are studied, which will be beneficial to explore the comprehensive optimization design of GPR dynamic and vibroacoustic properties.
Highlights
- Modals and vibration types of each order of the shell structure are presented.
- A numerical simulation method for vibration acoustic characteristics analysis is applied.
- Radiation acoustic characteristics with non-acoustic damping protection are studied.
- Optimal design for the shell structure of planetary gear reducer with low acoustic.
1. Introduction
The dynamic characteristics of a planetary gear reducer (PGR) exterior body have different influences due to their working conditions. In general, the exterior body of PGR exterior body is an elastic support that houses the structures of planetary gears, bearings, shafts, and other structures. When a PGR is in operation, internal excitations such as the meshing force of the tooth surface in the alternating meshing process of gears are transmitted to the exterior body through the structures. During the transmission process, the exterior body and the gear shaft influence each other. In other words, the EBS influences the forced vibration of the gear-shafting system and the characteristics of the vibrations and acoustics source (internal excitation force) of the PGR through the vibroacoustic radiation mechanism. Thus, the excitation load of the forced vibration causes the EBS to exterior body produce elastic vibrations by itself. However, the vibration energy inside the reducer is transferred to the adjacent hull structure (such as base and floating raft) and the cabin environment in the form of elastic vibrations of the exterior body, causing the hull structure vibration and cabin acoustics problem. Therefore, the exterior body characteristics of the excitation source in the EBS of the PGR and the influence of the hull structure vibroacoustics and the structural vibration as well as the structural impedance parameters of the dynamic characteristics of the PGR are closely related.
Many experimental and theoretical studies have analyzed the dynamic characteristics of the planetary gear. For example, Morgado et al. [1] studied the inherent vibration characteristics of a planetary gear system, established a time-varying dynamic model of a multi-DoFs system, and calculated its natural frequency and mode shape. The effects of rotation speed of a planetary frame and the supporting stiffness of a planetary gear on the natural characteristics of the system are also studied numerically. Renno and Mace [2] investigated the relationship between the natural frequency trajectories of the system in terms of the relative position of its gears and established the conditions for the generation of mode transition. They also described modal transition and its influence on the dynamic characteristics of a gear system using a quantitative method.
Considering the time-varying meshing stiffness, eccentricity error, and comprehensive meshing error of a planetary gear, Berry et al. [3] proposed a complete dynamic model of the planetary gear transmission system (PGTS). The dynamic response of the PGTS and the frequency domain history of the dynamic load coefficient are obtained using a numerical method. The nonlinear dynamic model of the PGTS is established by considering nonlinear factors such as time-varying meshing stiffness and gap error. They developed the model using the harmonic balance method and the Gill method. Mironova et al. [4] analyzed the time-varying characteristics of meshing stiffness, transmission error of the PGTS, and phase problem in the meshing process. Considering the time-varying stiffness of a rolling bearing, Suslin and Pilla [5] established a gear–bearing coupling dynamic model of a wind turbine PGTS and they calculated the frequency and dynamic response of the torsional vibration structure of a three-stage planetary gear. The dynamic meshing force of each gear pair and the dynamic contact force of the rolling bearing under random wind load are also discussed.
The acoustics inside the exterior body of a PGR, which is based on the optimized design of the EBS, is becoming increasingly significant [6]. Researchers require accurate vibroacoustic finite element analysis (FEA) models of the EBS for achieving a reliable design and conducting analysis [7]. However, experience has shown that vibration and acoustic predictions using these models are often did not correlate with the experimental results, so these models should be updated [8]. In the model updating framework, the influence of EBS and vibroacoustic parameters on the stiffness and damping modeling errors should be considered simultaneously to obtain an accurate estimation of those parameters [9, 10]. It should also be noted that acoustic absorption characteristics usually depend on the frequency dependent. This makes it difficult to update the vibroacoustic FEA model based on modal data.
In this perspective, a FEA method based on vibroacoustic response is proposed. Parameters related to the structural vibroacoustic model of the PGR exterior body are considered, and the coupling FEA models are modified. The effectiveness of the method is verified by numerically simulating the exterior body with a damping material used in three-dimensional PGR.
The exterior body structural vibroacoustic characteristics analysis is an important research topic in the optimization design of PGR [11]. In this study, the coupling vibration analysis models of the EBS, planetary gear, and shafting are established. Combined with the relationships between the exterior body structural parameters, as well as vibroacoustics, the leading transmission component and method of vibroacoustics are analyzed. The structural form and size of the exterior body are designed based on the impedance mismatch principle and the acoustic reduction technology of the damping acoustic material. Meanwhile, damping and sound-absorbing materials are reasonably selected. Finally, a low-acoustics structural design method for the EBS of the PGR is proposed. Such a design should significantly reduce the vibration and acoustics of the PGR in critical structures such as submarines.
In addition, vibration and noise reduction can be achieved by manipulating the dynamic characteristics of the exterior body with additional damping material [12-14]. The results show that stiffness and mass are two factors that affect the actual attenuation of the locally resonant damping structural exterior body. The locally resonant PGR is much heavier than the exterior body itself, which is disadvantageous to engineering applications [15-17]. The increasing demand for stable performance in harsh environments such as vibration and noise has led to the noise control problem of PGR exterior body to the forefront [18-20]. The results showed that the vibration of the EBS, sound field and damping coupling interface affected the noise in the PGR [21]. The vibration of the EBS produces noise, which in turn produces an additional response to the EBS because of the sound pressure [22-24]. Acoustic analysis of an EBS with an acoustic damping coupling system based on the finite element method can predict the vibration and noise of the entire structure of PGR in the initial design stage. This analysis can be widely used in the vibration and noise control design of heavy industrial reducers.
The remainder of the paper is structured as follows. Section 2 details the derivation of the motion differential equations of structural–acoustic coupling of a PGR exterior body based on numerical simulation. Section 3 analyzes the dynamic characteristics of the PGR exterior body. Section 4 demonstrates the radiation acoustic characteristics of a PGR exterior body without acoustic protection and damping materials. Furthermore, it details the optimal design of the EBS of a PGR with low acoustic. Finally, a composite structure that can attenuate the damping vibration and absorb the acoustics of the PGR exterior body is proposed.
2. Numerical analysis of the structural-acoustic coupled model
In this study, exterior body it is necessary to ensure that the dynamic characteristics of the PGR’s EBS remain unchanged with respect to the acoustic properties. An acoustic model of the EBS is established using median surface extraction, finite element partition, load, and boundary condition setting. Fig. 1 presents the general process of finite element analysis (FEA) of the EBS.
Fig. 1FEA process of a planetary gear reducer’s EBS
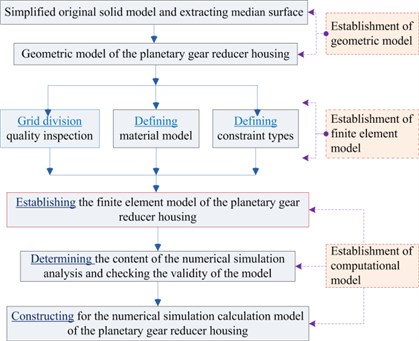
Based on the geometric topological structure model of the PGR’s exterior body with median surface characterization, Hyper Mesh software is used to extract the median of the reducer exterior body of upper and lower surfaces, and the end covers of the front and rear surfaces are extracted using HyperMesh. Coupled FEA models of the volumetric and surface grids are established, which are then imported to ABAQUS to construct the computational models for analysis. The reducer EBS with a relatively small thickness is discretized by an exterior body element, the thick base structure is discretized by the combination of exterior body and solid elements, and the restraint and damping layers are modeled by the laminated plate equivalent method. The simplified form of a multilayer damping material element of the EBS is presented in Fig. 2.
The damping layer is regarded as a rigid body moving in a region with an average acceleration. Furthermore, the damping layer is subjected to a concentrated force from the restraint layer and the lateral shear force on the edges of the polygon.
According to Newton’s second law, the dynamic differential equations of the primary and secondary damping layers [25] are derived as follows:
where , , .
Fig. 2Abridged general view of a multilayer damping material element of PGR exterior body
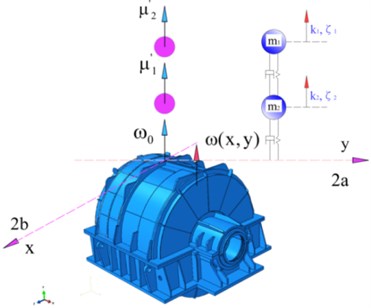
Unlike the traditional reducer exterior body, the basic exterior body of the reducer exterior body has two masses = 180 g and = 0.06, = 10.8 g with different spring damping constants and attached to exterior body. Then, 800 Hz. The edge lengths of the multilayer damping material sheet in the , , and directions are 220 mm and 220 mm, and the effective thickness of the damping layer 14.2 mm. The unit mass displacements of the primary and secondary damping layers are denoted by and, respectively.
To solve the specific problems in engineering applications, a reasonable analytical model should be adopted. The numerical analysis aims to restore the mathematical behavioral characteristics of an actual engineering system. Computational models are derived from geometric models, and highly efficient and compact geometrical models are a prerequisite for all subsequent work. Moreover, the establishment of effective models is based on dynamic analysis. The physical model of the PGR exterior body with damping mass is obtained via dynamic analysis to ensure that the structure of the fixed end, such as the floating raft and the base of the reducer exterior body, model would be simplified.
When an elastic structure is placed in a fluid medium, an interaction domain between the fluid and the interface of the elastic structure appears. The influence of structural vibration and boundary fluid is mutual. Furthermore, the entire system constitutes a structure–fluid coupling vibration problem. As shown in Fig. 3, the three-dimensional elastic structure of any shape placed in the fluid is considered, which is subjected to structural vibration problems from internal loads.
Given that the elastic structures are modeled by FEA, the motion differential equations of the elastic structures are expressed as follows:
where, for the coupled model, , , and represent the mass, damping, and stiffness matrices of elastic structures, respectively; , , and are the vectors of acceleration, velocity, and displacement of the elastic structure, respectively; and represents the vector of the structural load, is the matrix of the orthogonal transform, and represents the diagonal area matrix of the structural fluid boundary surface. The matrix generated by the product of and is expressed as a pressure vector of fluid in the negative direction transformed into a structural load vector on the principal material coordinate, and is the vector of fluid pressure. It is assumed that all pressures, displacements, and velocities are time-dependent functions. For the non-damping structural acoustic system, the discrete form of the dynamic equilibrium equation is:
where is the impedance matrix of the elastic structure. The coupled interface in a structural–acoustic system should satisfy the correlation condition of displacement and pressure. Then, Eq. (2) can be denoted as:
where , , and represent the structural velocity vector, structural load vector, and amplitude vector of the fluid pressure vector, respectively. Further, is the circular frequency of the non-damping structural acoustic system.
Fig. 3Coupled system model with elastic structure and boundary fluid medium
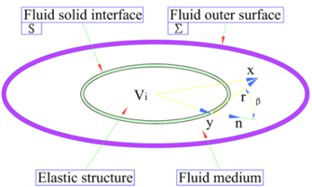
Fig. 4Schematic view of median surface forces and moments of damping layer
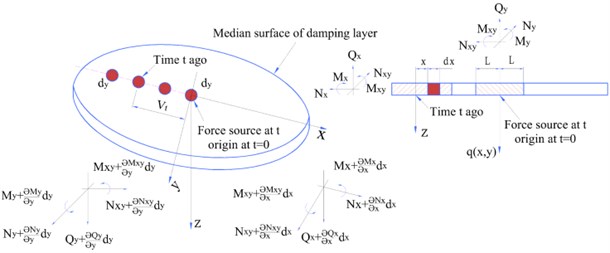
Similarly, the systems should also satisfy the correlation condition of the median surface forces and moments of the damping layer [26]. As shown in Fig. 4, the median surface forces of the damping layer can be derived as follows:
where , .
Thus, the median surface moments of the damping layer can be expressed as follows:
where , .
As indicated in Fig. 4, the interaction and energy transfer occur only when the bending mode causes a change in the fluid volume of the damping layer. The damping layer is one of the most important factors affecting the natural frequency of a PGR. The damping layer encompasses the exterior body and is fixed by the restraint layer. The mass and stiffness of the damping layer and the restraint layer are smaller than those of the exterior body. Therefore, the two layers are simplified as a mass point distribution on the steel EBS, as shown in Fig. 5.
Fig. 5Damping layer and constraint layer are simplified as a mass point distribution on the steel EBS: a) simplified structure model of the damping layer and b) simplified structure model of the constraint layer

a)

b)
Fig. 6First four orders of the PGR’s EBS (including the transmission shaft and the base): a) first-order mode (67.51 Hz), b) second-order mode (103.65 Hz), c) third-order mode (153.30 Hz), and d) fourth-order mode (145.29 Hz)
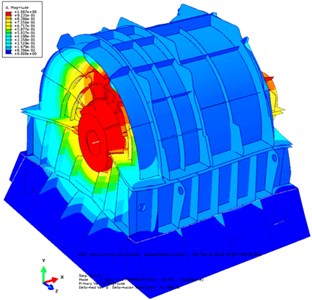
a)
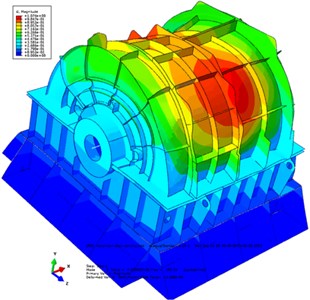
b)
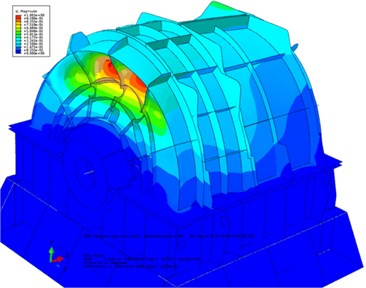
c)
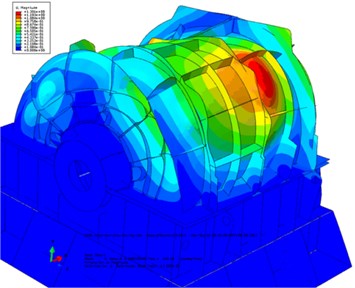
d)
The FEA model is different from the actual structure, and self-modeling defects of the model cannot completely reflect the actual structure. In this section, the effectiveness of the finite element mesh models is verified by the modal analysis method. The verification procedure is as follows:
1) A modal analysis of each individual component is performed to verify the finite element mesh quality, node association, and overlapping element problems of the component model.
2) A modal analysis of the integral FEA model is performed to verify the comprehensive and effective definition of various contact conditions among different components.
3) A modal analysis of the entire FEA model is proposed, and the modal mass, moment of inertia, and natural frequency of the model are obtained and compared with the actual structure.
In this study, an adequate number of modes within the range of the frequency extraction analysis step are extracted. The effectiveness of FEA model is verified by the first four-order modal analysis of the PGR structure, including the transmission shaft and the base (Fig. 6).
As illustrated in Fig. 6, the modal analysis revealed no distortion element in the FEA model of the EBS. Figure 6 indicates that the nodes are interconnected and that the FEA model is optimal. The total effective mass in the main direction of motion is 90 % higher than that of the criterion of the judgment of movable mass in the models. Therefore, the validity of the models is verified, and the models can be applied to the numerical simulation of the vibration response. In the following section, we use the finite element models to study the behavior of dynamic characteristics of the PGR exterior body.
3. Analysis of the dynamic characteristics of the PGR exterior body
In this section, the effects of acoustic treatment on the dynamic characteristics of the EBS are discussed, and the influences of different acoustic treatments and installation and connection conditions on the dynamic characteristics of the exterior body are considered. The vibration modes and natural frequencies of the exterior body before and after acoustic treatment are compared and analyzed. Table 1 describes the first 10 natural frequencies and modes of the EBS before and after the acoustic treatment. The first two orders of modal shapes of the front and rear EBS before and after the acoustic treatment are shown in Fig. 7. The figure also indicates that the results considered in the structure coupling state between the parts of the PGR are optimal, and the accuracy of the FEA model is proved. After acoustic treatment, the natural frequency of the exterior body is greatly increased. It can be observed that the change in the quality of the exterior body is greater than that of the stiffness. Before and after acoustic treatment, the modal shape changes significantly and has a certain similarity. Ignoring the influence of the transmission shaft and base, the first two orders of modes are dominated by local vibration, and the connection between the frontend plate and the upper exterior body is the most violent. In the following section, the radiation acoustic characteristics of the PGR exterior body with non-acoustic protection and damping materials are analyzed and studied.
Fig. 7First two orders of modal shapes in a cloud pattern in the actual installation state of the EBS before and after acoustic treatment: first-order mode before a) and after b) acoustic treatment and second-order mode before c) and after d) acoustic treatment
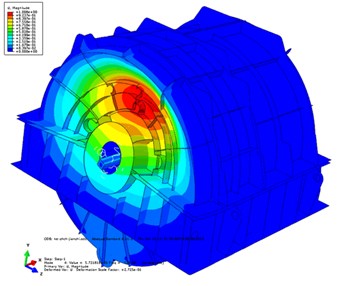
a)
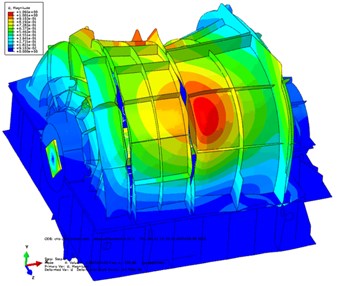
b)
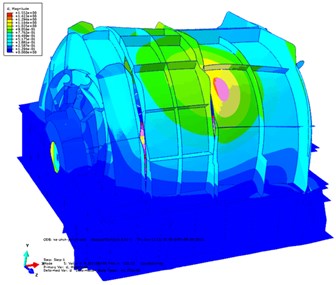
c)
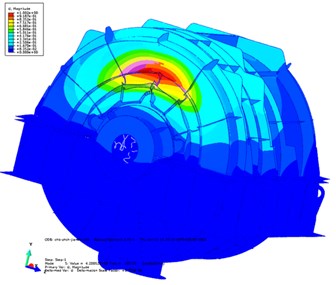
Table 1Description of the first 10 natural frequencies/modes of the EBS before/after acoustic treatment
Orders | Pre-processing natural frequency (Hz) | Pre-processing vibration mode description | Post-processing natural frequency (Hz) | Post-processing vibration mode description | Change rates |
1 | 121.64 | Vibration of the frontend plate in –direction | 101.93 | Torsional pendulum vibration of the upper part of the exterior body | –16.17 % |
2 | 126.78 | Torsional pendulum vibration of the upper part of the exterior body | 104.41 | Vibration of the frontend plate in -direction | –17.65 % |
3 | 130.32 | Vibration of the frontend plate in –direction | 112.86 | Vibration of the frontend plate in -direction | –13.39 % |
4 | 146.74 | Transmission shaft vibration | 124.57 | Bending vibration of the upper part of the exterior body | –15.11 % |
5 | 155.52 | Transmission shaft vibration | 139.68 | Transmission shaft vibration | –10.19 % |
6 | 167.92 | Vibration of the frontend plate in -direction | 145.97 | Transmission shaft vibration | –13.07 % |
7 | 188.13 | Vibration of the frontend plate in -direction | 153.86 | Bending vibration of the front part of the exterior body | –18.22 % |
8 | 193.47 | Local vibration of the lower exterior body | 161.92 | Local vibration of the lower exterior body | –16.31 % |
9 | 203.46 | Holistic torsional vibration of the exterior body | 163.88 | Torsion of the frontend plate and local vibration of the lower exterior body | –19.45 % |
10 | 212.41 | Local torsion of the frontend plate | 168.69 | Local torsion of the frontend plate and lower exterior body | –20.58 % |
4. Radiation acoustic characteristics with no acoustic protection or damping materials
Before calculating and analyzing the vibroacoustic characteristics of the EBS, it is necessary to analyze the response of each part to the excitation force. The transfer function can be used to evaluate the response of different parts of the exterior body to excitation, thus optimizing the structural characteristics.
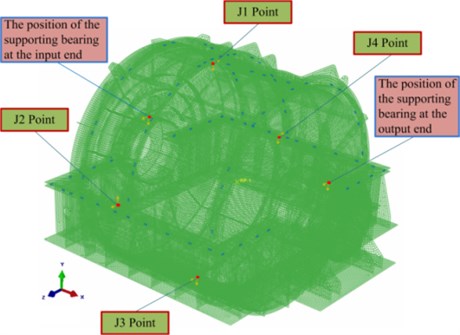
The small vibration of the planetary reducer exterior body is caused by the excitation force; hence, the response signal (displacement, velocity, or acceleration) is obtained at the examination site where the excitation source is present. Fig. 8 depicts a schematic diagram of the positions of the excitation points of the EBS. As observed clockwise from the input side to the output end, the position of the excitation force exterior body is located on the bearings at the input exterior body and output ends of the exterior body, respectively, where point 1 is the direction of 12:00, point 2 the direction of 03:00, point 3 the direction of 06:00, and point 4 the direction of 06:00, and is the horizontal direction and the vertical direction.
Fig. 8Schematic diagram of positions of excitation points of the EBS
Based on the established FEA models, the BEM flow field is established at a distance of 5 m from the EBS. A square data collection grid is established at a distance of 1.0 m from the outer layer of the damping plate, as shown in Fig. 9.
Fig. 9Calculation model for the radiated acoustic sound field
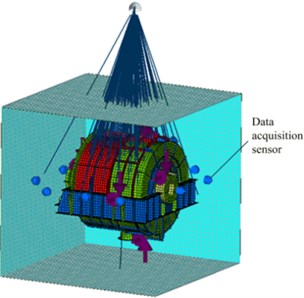
Fig. 10Layout of acoustic test points
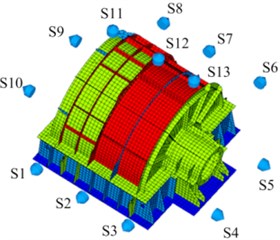
A total of 13 data collectors are arranged on each surface of the square (acoustic test points), and the BEM flow field is manually connected to the boundary element grid of the exterior body subsystem. Figure 9 illustrates the establishment of the BEM flow field and boundary element calculation model for the radiated acoustic sound field. Fig. 10 presents the layout of the acoustic test points on the EBS. The material of the PGR exterior body is Q235 steel. The radiated acoustics of the EBS is estimated, and the proportion of acoustic radiation of each part of the exterior body in the total acoustics is evaluated. The contribution of acoustics and the influence of structural parameters on acoustic characteristics are analyzed.
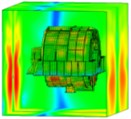
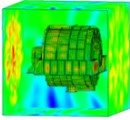
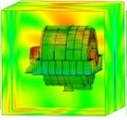
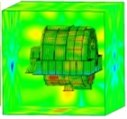
Considering the EBS in practice, the loss factor of the EBS is set to 0.002. Here, it is assumed that the loss factor exterior body does not change with the frequency. To compare the radiated acoustics in each part of the exterior body, the exterior body is divided into four parts: frontend face, large circumferential plate, small circumferential plate, and backend panel (Fig. 11). Figs. 12, 13, 14, and 15 demonstrate the spatial distributions of the acoustic radiation sound pressure on the backend panel, small and large circumferential plates, and frontend face, respectively.
Fig. 11Partition of the EBS
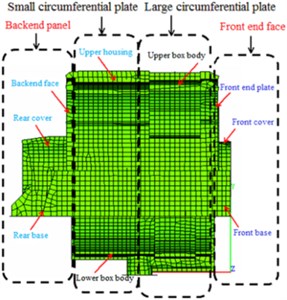
Fig. 12Sound pressure on the backend panel (spatial distribution)

a) 200 Hz

b) 400 Hz
c) 800 Hz
d) 1,600 Hz
Fig. 13Sound pressure on the small circumferential plate (spatial distribution)

a) 200 Hz
b) 400 Hz
c) 800 Hz
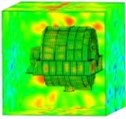
d) 1,600 Hz
Fig. 14Sound pressure on the large circumferential plate (spatial distribution)
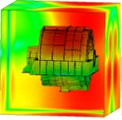
a) 200 Hz
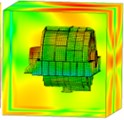
b) 400 Hz

c) 800 Hz

d) 1,600 Hz
Fig. 15Sound pressure on the frontend face (spatial distribution)
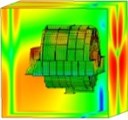
a) 200 Hz
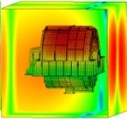
b) 400 Hz
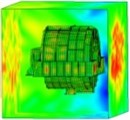
c) 800 Hz
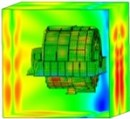
d) 1,600 Hz
These figures illustrate that the radiation sound pressure of the frontend face and the large circumferential plate is larger than that of the backend panel and the small circumferential plate in the low-frequency section (≤ 400 Hz). The vibration between the frontend face and the large circumferential plate is relatively large. In the medium- and high-frequency ranges (> 400 Hz), the radiated sound pressure of the backend panel and the small circumferential plate increases gradually, and the sound pressure is higher than those of the frontend face and the large circumferential plate. Therefore, in the medium- and high-frequency bands, the vibrations of the backend panel and the small circumferential plate are the main manifestations.
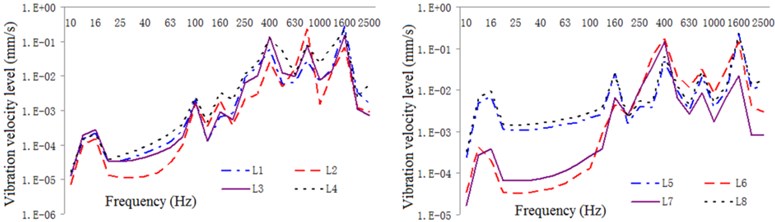
Fig. 16One-third oct response curve of vibration acceleration in typical parts of the exterior body under original structural conditions
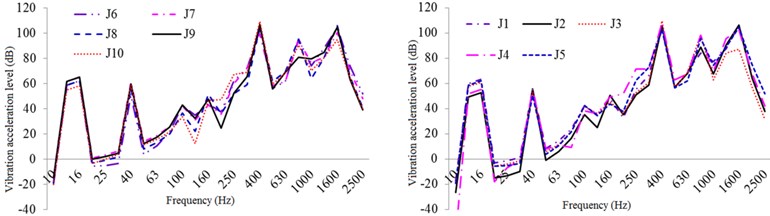
Fig. 17One-third oct response curve of vibration acceleration in typical parts of the exterior body under constrained damping conditions
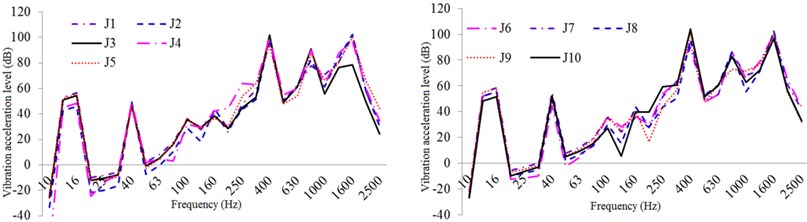
Fig. 18One-third oct response curve of vibration acceleration class of typical parts of the exterior body under restrained damping and acoustic protection conditions
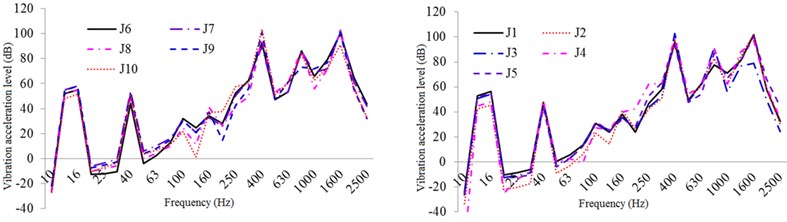
Fig. 19One-third oct response curve of vibration intensity in typical parts of the exterior body under original structural conditions
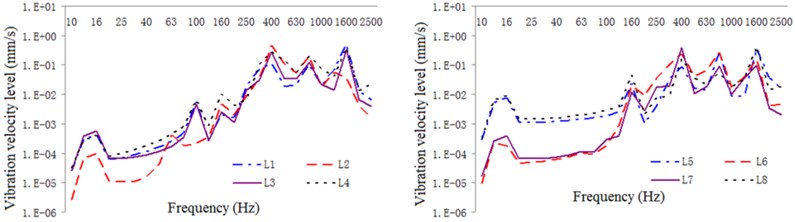
Fig. 20One-third oct response curve of vibration intensity in typical part of the exterior body under constrained damping condition
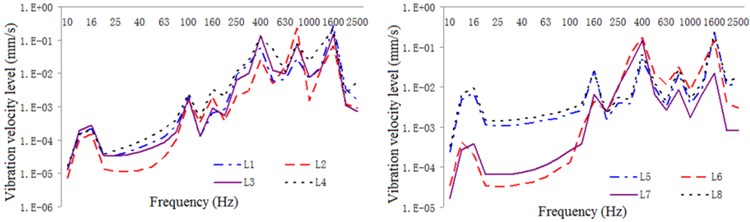
Fig. 21One-third oct response curve of vibration intensity of typical parts of the exterior body under restrained damping and acoustic protection conditions
To better understand the feasibility of the practical design of the EBS, the design is re-simulated on Hyperworks. The final optimal design scheme is as follows.
Both the acoustic insulation layer and the restraint layer are made of a Q235 steel EBS, the thicknesses of which are set to 5 mm. The thickness of the damping layer is set to 30 mm, Young’s modulus to 8 × 106 Pa, and loss factor to 0.5. As a sound-absorbing protective measure, we use 30-mm-thick mineral cotton. The curves of vibration acceleration, velocity, and sound pressure level for the test points at typical locations before and after the use of acoustic materials are shown in Figs. 16-24.
Fig. 22One-third oct response curve of acoustic radiation from typical parts of the exterior body under original structural conditions
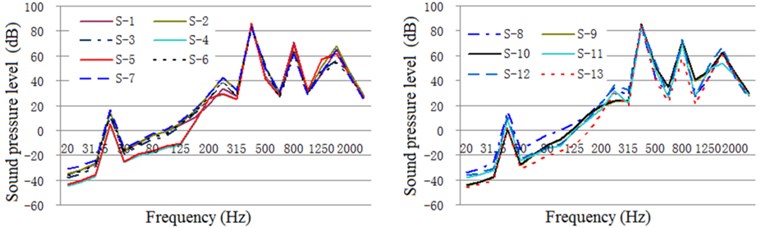
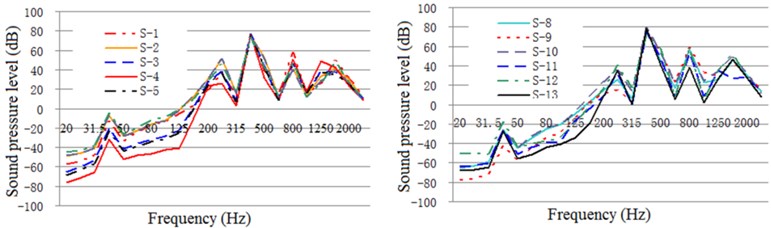
As illustrated in these figures, the damping layer, sound insulation layer, and sound absorption protection measures all decrease the vibration and noise levels of the EBS. Vibration acceleration, vibration velocity, and radiation noise of the EBS are reduced by 4-6 dB, 4-7 dB, and 7-10 dBA, respectively, where the effect of the constrained damping layer on the vibration acceleration and vibration intensity of the EBS is between 4 and 6 dB. The influence of the restrained damping layer on the sound radiation exterior body is between 7 and 10 dBA. Protective measures such as absorption and isolation of sound had little effect on the vibration of the EBS, and its effect on sound radiation exterior body is between 4 and 5 dBA.
Before the EBS is acoustically treated, the sound pressure emitted from the backend panel and the small circumferential plate of each part of the exterior body is relatively large, which is the dominant component of the acoustics. Therefore, in practical engineering applications, researchers should focus more on the field of controlling structural vibration and acoustics. In the following section, the optimal design of the EBS of a PGR with low acoustics is detailed.
Fig. 23One-third oct response curve of acoustic radiation from typical parts of the exterior body under constrained damping conditions
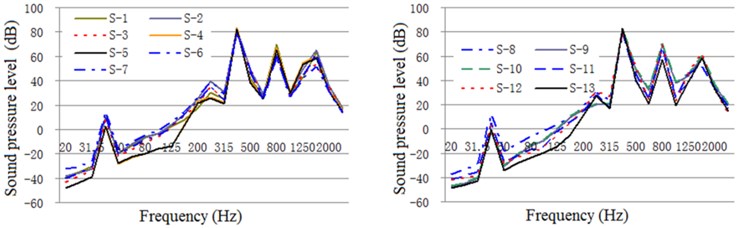
Fig. 24One-third oct response curve of acoustic radiation from typical parts of the exterior body under restrained damping and acoustic protection conditions
5. Optimal design of the EBS of PGR with low acoustics
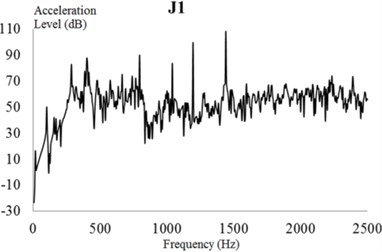
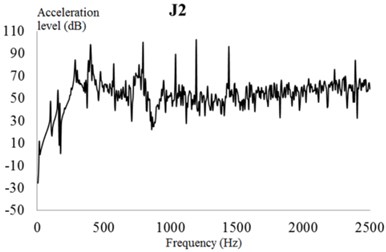
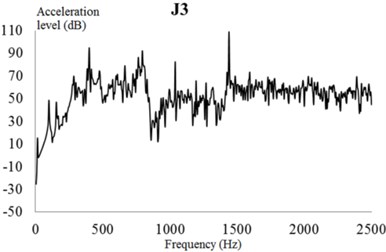
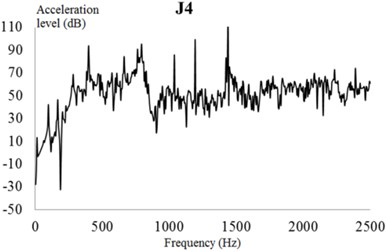
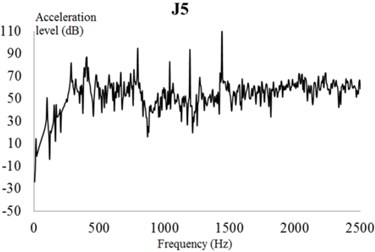
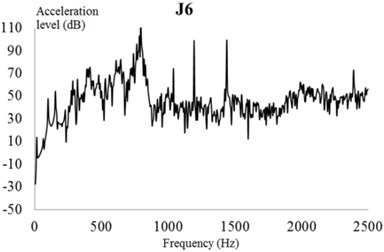
The input characteristics of the EBS should be presented in the dynamic response analysis. In this section, the excitation force is used as input to the frequency domain by a fast Fourier transform, and the frequency spectrum characteristics of the meshing frequency and harmonic frequency are analyzed in detail. The excitation force in the frequency domain is used as an input parameter to analyze the harmonic response of the exterior body. The vibration acceleration response value and vibration acceleration level of each check point at the machine foot are shown in Fig. 25.
In these figures, the vibration acceleration level curves represent each check point with acoustic protection and damping materials for reference. Compared with the naked EBS of the PGR exterior body, the protected exterior body exhibits evident wave peaks in the acceleration response curves around the excitation frequencies of 400, 800, and 1440 Hz. Because the magnitude of the excitation force of the EBS at this frequency is large, the response value of the EBS is also the largest.
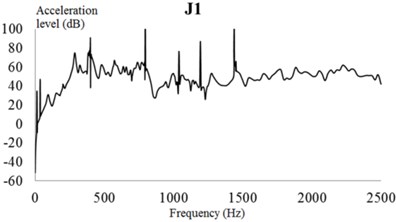
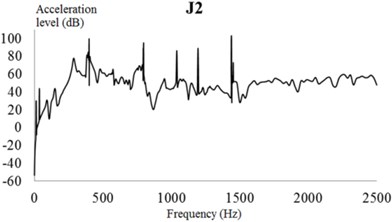
Correspondingly, the vibration response acceleration of the exterior body at a typical excitation frequency is considered under the action of the actual excitation load. Combined with the actual working conditions, a constrained damping layer is adopted for the EBS. Based on the analysis of the dynamic characteristics, vibration transfer characteristics, and radiation noise characteristics of the EBS, the structures of the frontend and backend plates, upper exterior body, and upper cover of the PGR exterior body are weaker. Therefore, each part is thickened by 10 mm without changing the structural form. Then, the FEA model of the modified exterior body is reconstructed. Through the theory of the modal loss factor calculation for the constrained damping layer, the composite loss factor of the exterior body with the constrained damping layer is 0.012. The vibration acceleration response of the building structure under the action of a practical excitation constrained damping layer is shown in Fig. 26.
Fig. 25Vibration acceleration level of each check point on the gear exterior body. Vibration acceleration levels of check points: a) 1, b) 2, c) 3, d) 4, e) 5, and f) 6
a)
b)
c)
d)
e)
f)
As illustrated in Fig. 26, the vibration response curve of the additional constrained damping layer is consistent with that of the unconstrained damping layer. The acceleration level of each test point is not more than 105 dB in the frequency domain. Moreover, the peaks of the acceleration response curve appear at 399, 797, and 1,439 Hz. These results show that the constrained damping layer will only affect the acceleration response of the EBS near 400, 800, and 1,440 Hz, but will not affect the change of the acceleration curve at other frequencies.
Fig. 26Vibration acceleration of each check point considering the constrained damping layer (CDL). Vibration accelerations of check points: a) 1, b) 2, c) 3, d) 4, e) 5, and f) 6
a)
b)
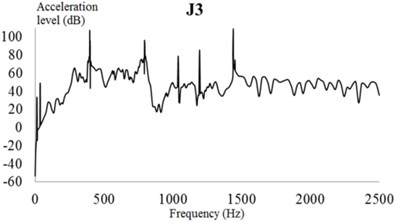
c)
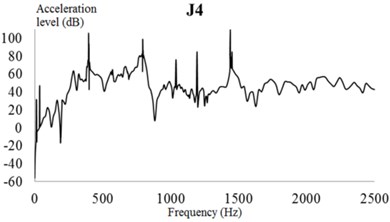
d)
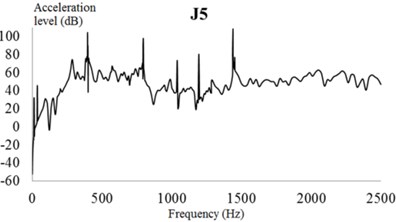
e)
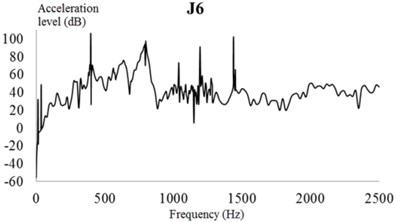
f)
6. Conclusions
In this paper, the structural–acoustic coupled vibration and noise analysis model of PGR exterior body is proposed through numerical analysis. The optimal design of the EBS and the vibration noise characteristics are analyzed in detail, and the effects of auxiliary vibration absorption and noise reduction on the evaluation are verified. This study draws the following conclusions:
1. Based on the optimized design and vibration noise characteristics from the EBS analysis, the following conclusions are drawn:
1.1) The input and output end plates of the EBS are weak relative to the circumferential stiffness. Considering the influence of exterior body shafting and other factors, strengthening the end structure cannot effectively improve the dynamic characteristics of the end part of the exterior body.
1.2) The EBS has strong vibration line spectrum near the meshing frequencies of 399, 797, and 1,439 Hz, and the vibration modes are the most intensive, which is the focus of the optimization of the exterior body dynamic characteristics.
2. Based on the results of the analysis of the exterior body structural damping vibration absorption and acoustic protection design of the exterior body are as follows:
2.1) When the constrained damping measures for vibration absorption and noise reduction exterior body are not adopted, the structural vibration acceleration is between 107 and 110 dB, the vibration velocity is between 0.4 and 0.55 mm/s, and the radiated noise is approximately 85 dBA.
2.2) The implementation of the measures starkly decreases the vibration and sound radiation exterior body. The measures lead to the structural vibration acceleration plummeting to 102-105 dB, vibration velocity to 0.16-0.30 mm/s, and radiated noise to 80-83 dBA.
2.3) Even with the protective measures in place, the vibration level of the exterior body remains basically unchanged, but the sound radiation of the EBS decreases to 73-78 dB.
3. After adopting the auxiliary measures of damping vibration reduction and sound insulation protection, the vibration acceleration, vibration velocity, and radiation noise of the EBS are reduced by 4-6, 4-7, and 7-10 dBA, respectively.
References
-
Morgado T. L. M., Branco C. M., Infante V. A. failure study of housing of the gearboxes of series 2600 locomotives of the Portuguese Railway Company. Engineering Failure Analysis, Vol. 15, Issues 1-2, 2008, p. 154-164.
-
Renno J. M., Mace B. R. Calculating the forced response of cylinders and cylindrical shells using the wave and finite element method. Journal of Sound and Vibration, Vol. 333, Issue 21, 2014, p. 5340-5355.
-
Berry A., Robin O., Pierron F. Identification of dynamic loading on a bending plate using the virtual fields method. Journal of Sound and Vibration, Vol. 333, Issue 26, 2014, p. 7151-7164.
-
Mironova T. B., Prokofiev A. B., Sverbilov V. Y. The finite element technique for modelling of pipe system vibroacoustical characteristics. Procedia Engineering, Vol. 176, 2017, p. 681-688.
-
Suslin A., Pilla C. Study of Loading in Point-involute Gears. Procedia Engineering, Vol. 176, 2017, p. 12-18.
-
Hwang H. D., Maxit L., Ege K., Gerges Y., Guyader J-L. SmEdA vibro-acoustic modelling in the mid-frequency range including the effect of dissipative treatments. Journal of Sound and Vibration, Vol. 393, 2017, p. 187-215.
-
Lin T. L., Zhang K. An analytical study of the free and forced vibration response of a ribbed plate with free boundary conditions. Journal of Sound and Vibration, Vol. 422, 2018, p. 15-33.
-
Zhou H. A., Zhao Y. G., Wu H. Y., Meng J. B. The vibroacoustic analysis of periodic structure-stiffened plates. Journal of Sound and Vibration, Vol. 481, 2020, p. 115402.
-
Sánchez M. B., Pleguezuelos M., Pedrero J. I. Approximate equations for the meshing stiffness and the load sharing ratio of spur gears including hertzian effects. Mechanism and Machine Theory, Vol. 109, 2017, p. 231-249.
-
Acri A., Nijman E., Conrado E., Offner G. Experimental structure-borne energy flow contribution analysis for vibro-acoustic source ranking. Mechanical Systems and Signal Processing, Vol. 115, 2019, p. 753-768.
-
Garambois P., Donnard G., Rigaud E., Perret-Liaudet J. Multiphysics coupling between periodic gear mesh excitation and input/output fluctuating torques: Application to a roots vacuum pump. Journal of Sound and Vibration, Vol. 405, 2019, p. 158-174.
-
Wu H., Wu P. B., Li F. S., Shi H. L., Xu K. Fatigue analysis of the gearbox housing in high-speed trains under wheel polygonization using a multibody dynamics algorithm. Engineering Failure Analysis, Vol. 100, 2019, p. 351-364.
-
13. Hu W. G., Liu Z. M., Liu D. K., Hai X. Fatigue failure analysis of high speed train gearbox housings. Engineering Failure Analysis, Vol. 73, 2017, p. 57-71.
-
Weis P., Kučera Ľ., Pecháč P., Močilan M. Modal analysis of gearbox housing with applied load. Procedia Engineering, Vol. 192, 2017, p. 953-958.
-
Liang X., Zuo M. J., Feng Z. Dynamic modeling of gearbox faults: A review. Mechanical Systems and Signal Processing, Vol. 98, 2018, p. 852-876.
-
Yang Y., Fenemore C., Kingan M. J., Mace B. R. Analysis of the vibroacoustic characteristics of cross laminated timber panels using a wave and finite element method. Journal of Sound and Vibration, Vol. 494, 2021, p. 115842.
-
Ege K., Roozen N. B., Leclère Q., Rinaldi R. G. Assessment of the apparent bending stiffness and damping of multilayer plates; modelling and experiment. Journal of Sound and Vibration, Vol. 426, 2018, p. 129-149.
-
Arasan U., Marchetti F., Chevillotte F., Tanner G., Chronopoulos D., Gourdon E. On the accuracy limits of plate theories for vibro-acoustic predictions. Journal of Sound and Vibration, Vol. 493, 2021, p. 115848.
-
Guo Y., Eritenel T., Ericson T. M., Parker R. G. Vibro-acoustic propagation of gear dynamics in a gear-bearing-housing system. Journal of Sound and Vibration, Vol. 333, Issue 22, 2014, p. 5762-5785.
-
Kosała K. Calculation models for analysing the sound insulating properties of homogeneous single baffles used in vibroacoustic protection. Applied Acoustics, Vol. 146, 2019, p. 108-117.
-
Marchetti F., Ege K., Leclère Q., Roozen N. B. On the structural dynamics of laminated composite plates and sandwich structures; a new perspective on damping identification. Journal of Sound and Vibration, Vol. 474, 2020, p. 115256.
-
Rosa S. D., Desmet W., Ichchou M., Ouisse, M., Scarpa F. Vibroacoustics of periodic media: multi-scale modelling and design of structures with improved vibroacoustic performance. Mechanical Systems and Signal Processing, Vol. 142, 2020, p. 106870.
-
Bi S. F., Ouisse M., Foltête E., Jund A. Virtual decoupling of vibroacoustical systems. Journal of Sound and Vibration, Vol. 401, 2017, p. 169-189.
-
Tomilina T. M. New approaches to design of structures with required vibroacoustic properties. Procedia Engineering, Vol. 106, 2015, p. 350-353.
-
Daneshjou K., Talebitooti R., Kornokar M. Vibroacoustic study on a multilayered functionally graded cylindrical shell with poroelastic core and bonded-unbonded configuration. Journal of Sound and Vibration, Vol. 393, 2017, p. 157-175.
-
Rohan E., Lukeš V. Homogenization of the vibro-acoustic transmission on perforated plates. Applied Mathematics and Computation, Vol. 361, 2019, p. 821-845.
About this article
The authors would like to thank the Northeast Forestry University (NEFU), Heilongjiang Institute of Technology (HLJIT), and the Harbin Institute of Technology (HIT) for their support.
The research topic is supported by the Doctoral Research Startup Foundation Project of Heilongjiang Institute of Technology (Grant No. 2020BJ06, Yongmei Wang, HLJIT), the Natural Science Foundation Project of Heilongjiang Province (Grant No. LH2019E114, Baixue Fu, HLJIT), the Basic Scientific Research Business Expenses (Innovation Team Category) Project of Heilongjiang Institute of Engineering (Grant No. 2020CX02, Baixue Fu, HLJIT), the Special Project for Double First-Class-Cultivation of Innovative Talents (Grant No. 000/41113102, Jiafu Ruan, NEFU), the Special Scientific Research Funds for Forest Non-profit Industry (Grant No.201504508), the Youth Science Fund of Heilongjiang Institute of Technology (Grant No. 2015QJ02), and the Fundamental Research Funds for the Central Universities (Grant No. 2572016CB15).
