Research on dynamic characteristic of planetary gear system based on bond graph method

1. Introduction

The dynamic characteristics of planetary gear system will directly affect the healthy and stable running state of the whole transmission system [1]. Due to the existence of ulnar clearance, time-varying meshing stiffness and comprehensive transmission error in planetary gear system, the rules of dynamic characteristics of planetary gear system are extremely complex, which brings great challenges to the kinematics and dynamics design, as well as the reasonable design and accurate control of system stability [2, 3].

The dynamics of planetary gear transmission system, focusing on finding accurate and efficient analysis model, and exploring the dynamic response and excitation mechanism of the system [4, 5]. The dynamic characteristics and system stability play a very important role in advanced design and fatigue analysis. However, the traditional gear train modeling method starts from the perspective of simplification and equivalence, thus some important factors affecting the system are omitted [6]. As a result, the dynamic characteristics of the gear system are much different from the actual situation, and lost its guiding significance for practical application.

2. The bond graph model of planetary gear system

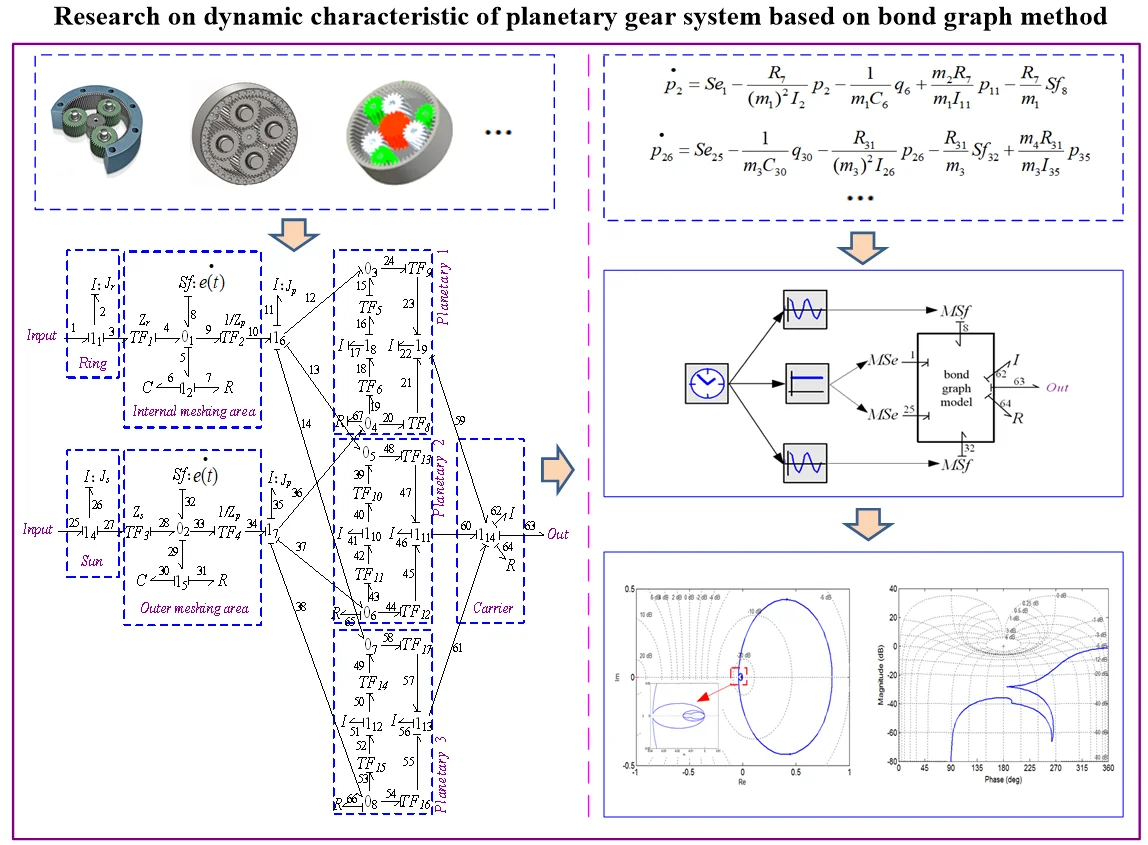
This paper takes NGW gear train as the research object. According to the bonding diagram modeling principle, the bond graph model of planetary gear system is obtained, as shown in Fig. 1.

3. Dynamics equation of state for gear system

State variables $\mathbf{Y}=\left[p_2,q_6,p_{11},p_{17},p_{22},p_{26},q_{30},p_{35},p_{41},p_{46},p_{51},p_{56},p_{62}\right]$. According to gear train bond graph model, the state equation used to describe the motion state of the epicyclic unit was be obtained. When ${\dot{p}}_{17}=e_{17}$, ${\dot{p}}_{22}=e_{22}$, ${\dot{p}}_{41}=e_{41}$, ${\dot{p}}_{46}=e_{46}$, ${\dot{p}}_{51}=e_{51}$, ${\dot{p}}_{56}=e_{56}$, as shown in Eq. (1-6):

where, $m_i$ is the conversion coefficient of the converter, $i=$1, 2, …, 22; $S{e}_1$ and $S{e}_{25}$ are potential sources of input; $S{f}_8$ and $S{f}_{32}$ are steady-state transmission errors.

Fig. 1The bond graph model of planetary gear system

4. Numerical simulation and discussion

4.1. Simulation condition setting

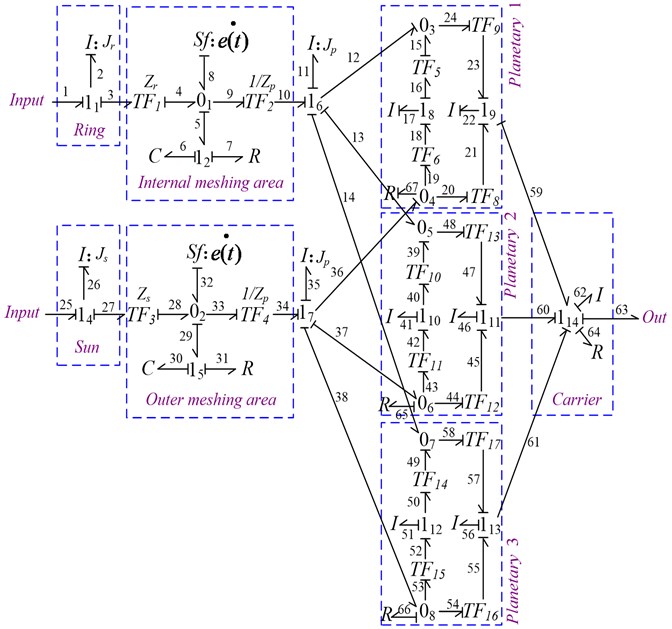
The simulation model is shown in Fig. 2. $M{S}_{e1}$ and $M{S}_{e2}$ are as the input end, $MS{f}_8$ and $MS{f}_{32}$ are used to represent the derivatives of steady transmission errors, as show in Table 1.

Table 1Simulation parameter

Number of teeth	$Z_s=$ 19, $Z_p=$31, $Z_r=$81	Radius of indexing circle	$R_s=$0.0285 m, $R_p=$0.0465 m, $R_r=$0.1215 m, $R_h=$0.075 m
Moment of inertia	$I_s=$0.0015 Kg·m2, $I_p=$0.0094 Kg·m2, $I_r=$0.1510 Kg·m2, $I_h=$0.0491 Kg·m2	Meshing stiffness	$Kg=$1.8e8 N/m
		Torsional stiffness of shaft	$Ks=$2.0e8 N/m
		Moment of inertia of shaft	$I_f=$0.0036 Kg·m2
Meshing damping	$C_g=$2000 N·s·m-1	Support damping	$C_v=$1800 N·s·m-1
Derivative of steady state transmission error		$\dot{e}\left(t\right)=0.0027\times \mathrm{c}\mathrm{o}\mathrm{s}(28t+21pi)$

Fig. 2Simulation model of planetary gear system

4.2. Analysis of simulation results

4.2.1. Gear ring input

It was be comprehended from Fig. 3(a) that the open loop transfer function of the system is a non-minimum phase system. The Bode diagram shown in Fig. 3(b), the phase margin $\gamma \left({\omega }_c\right)=\infty$, and the amplitude margin $K_g=$ 35.9 dB > 0 (7.09 rad /s). The Nyquist diagram shown in Fig. 3(c), the open-loop frequency characteristic curve of the system does not enclose the point (–1, $j_0$). Nichols diagram shown in Fig. 3(d), the vertical axis is the logarithm of amplitude and the horizontal axis is the phase Angle, which reflects the changing relationship between amplitude and phase Angle. The closed-loop system of planetary gear train is unstable under such simulated conditions.

4.2.2. Sun gear input

Similarly, it is be concluded from Fig. 4 that the closed loop system of the planetary gear train is unstable.

Fig. 3The stability of planetary gear system

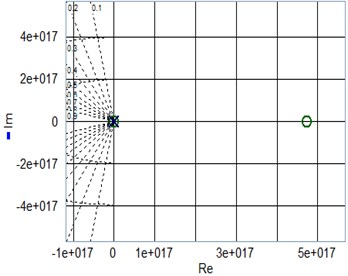
a) Pole-Zero

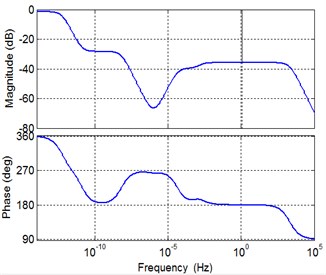
b) Bode

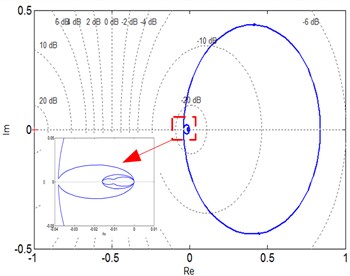
c) Nyquist

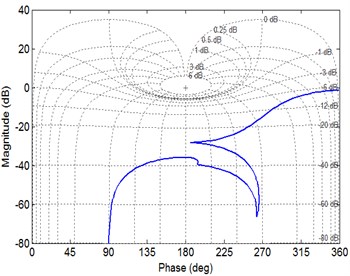
d) Nichols

Fig. 4The stability of planetary gear system

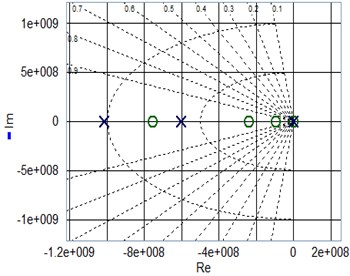
a) Pole-Zero

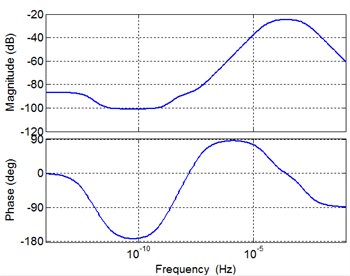
b) Bode

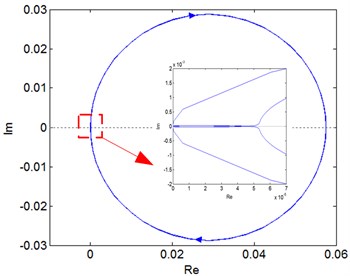
c) Nyquist

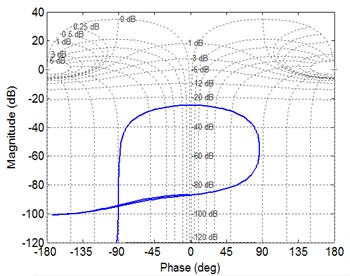
d) Nichols

5. Conclusions

The bond graph model of the planetary gear system was established, which solved the problem that traditional modeling method could not accurately reflect the dynamic characteristics of the gear system. Then, state space and state equation of gear train dynamics are derived on the basis of bond graph model. Zero-pole diagram, Bode diagram, Nyquist diagram and Nichols diagram, are calculated by using numerical simulation method, and the dynamic rule of the gear system is reflected.