Hydroelastic oscillation of a plate resting on Pasternak foundation

Kondratov, Dmitry V.; Mogilevich, Lev I.; Popov, Victor S.; Popova, Anna A.

doi:10.21595/vp.2017.18358

Vibroengineering Procedia

Browse Procedia

Published: 30 June 2017

Check for updates

Hydroelastic oscillation of a plate resting on Pasternak foundation

Dmitry V. Kondratov¹

Lev I. Mogilevich²

Victor S. Popov³

Anna A. Popova⁴

¹Russian Presidential Academy of National Economy and Public Administration, Saratov, Russian Federation

^{2, 3, 4}Yuri Gagarin State Technical University of Saratov, Saratov, Russia

Corresponding Author:

Dmitry V. Kondratov

Cite the article Download PDF

Downloads 1418

CrossRef Citations 1

Abstract

The bending oscillations of the plate, resting in Pasternak foundation and interacting with a vibrating stamp through a thin layer of viscous incompressible liquid, are investigated. On the basis of hydroelasticity problem solution, the laws of the plate deflections and pressure in the liquid are found. The functions of the deflections amplitude distribution and liquid pressure along the channel are constructed. The obtained results allow to define oscillations resonance frequencies and to study viscous liquid interaction with elastic plates, resting on Pasternak foundation.

1. Introduction

The investigation of elastic construction elements oscillation with consideration as of their interaction with heterogeneous bodies, as of elastic pliability of the foundations, on which they are rested, presents an important issue of contemporary technology. For example, references [1-4] study the oscillations and stability of multi-layer beams and plates, rested on an elastic foundation under the influence of local and distributed loads of various origins. Winkler and Pasternak models are used for foundation reactions modeling. Reference [5] is devoted to numerical investigation of rectangular plates natural oscillations, the plates being fully plunged into motionless ideal liquid or floating on its free surface. The various variants of the plates fixing are considered. The analogous investigation for the case of rectangular plates interacting with the ideal liquid flow is made in reference [6]. The plate eigenfrequencies analysis is made and the flow critical velocities, corresponding to stability loss, are found. The issues of the chaotic oscillations of the plate, interacting with an ideal incompressible liquid flow, are studied in reference [7]. However, the liquid dumping properties, conditioned by its viscosity are excluded from consideration. Reference [8] deals with investigating vibrations of endlessly long beam on viscous liquid layer. The investigation of the cross oscillations of the elastic-fixed solid wall of the flat channel of finite sizes is made in [9]. Hydroelastic oscillations of cantilever beam, plunged into a viscous incompressible liquid, are investigated in reference [10]. The problem of vibrating discs dynamics interaction with a layer of viscous incompressible liquid between them is solved in reference [11]. The present paper studies the case when the discs are considered being solid, as well as the case with one of the discs being elastic. The analogous problem in a flat setting for the two vibrating plates of finite sizes is studied in reference [12]. Reference [13] investigates hydroelastic oscillation of the beam in a viscous liquid flow for the case of piezo-electric elements with the aim of obtaining energy from the flow. Reference [14] deals with solution of the problem of the bending hydroelastic oscillations of the plate, forming the narrow channel wall under the impact of the viscous liquid pulsating layer. The forced hydroelastic oscillations of the three-layered round plate interacting with viscous incompressible liquid layer under the channel foundation vibration are investigated in [15]. Alongside with this, the evaluation of foundation elasticity impact on hydroelastic oscillations is of theoretical and practical interest. Reference [16] investigates the oscillations of the membrane, resting on Winkler elastic foundation, the membrane being on the bottom of reservoir, filled with an ideal incompressible liquid with a free surface. The hydroelastic oscillations of the rectangular plates, resting on Pasternak foundation and interacting with an ideal incompressible liquid with a free surface, are investigated in references [17-19]. The investigation of the oscillations of the plate, resting on the elastic Winkler foundation and interacting with viscous incompressible liquid pulsating layer, was made in references [20-22].

2. Statement of the problem

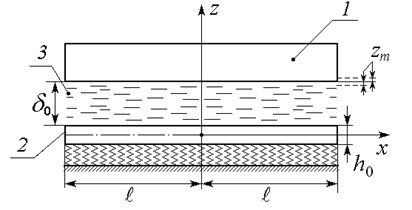
Let us consider the elastic plate 2 resting on Pasternak foundation and interacting with a vibrating stamp 1 through the viscous incompressible liquid layer 3 between them (Fig. 1). We will study the problem in a flat setting. Let us connect Cartesian coordinate $O x z$ with the center of the plate medium surface in an undisturbed state. The stamp movement takes place under the assigned harmonic law in a vertical plane. The plate possesses the thickness $h_{0}$ , the length 2 $l$ . It is simply supported on the edges. The viscous liquid fully fills a narrow channel, formed by a plate and a vibrating stamp, the medium thickness of a liquid layer in the channel being $δ_{0} ≪ l$ and the plate deflection amplitudes being significantly less than $δ_{0}$ . The liquid at the edges freely leaks out in the same liquid with a constant pressure level $p_{0}$ . Taking into account the fact, that liquid viscosity consideration leads to quick going down of transition processes, we can exclude the initial processes impact from the very beginning [23]. Further, we will consider the stationary forced harmonic oscillations.

Fig. 1A schematic diagram of a narrow slit channel on Winkler foundation

3. The theory

We will present the law of the stamp movement in the form of:

1

z = z_{m} f (ω t), f (ω t) = s i n ω t,

where $z_{m}$ is the stamp oscillation amplitude, $ω$ is the oscillation frequency, $t$ is the time.

Due to the channel narrowness, we will consider the liquid dynamics in it in terms of hydrodynamic lubrication theory, i.e. we investigate liquid creeping flow in the channel, which is described by the equation [24]:

2

\frac{1}{ρ} \frac{\partial p}{\partial x} = ν (\frac{\partial^{2} u_{x}}{\partial x^{2}} + \frac{\partial^{2} u_{x}}{\partial z^{2}}), \frac{1}{ρ} \frac{\partial p}{\partial z} = ν (\frac{\partial^{2} u_{z}}{\partial x^{2}} + \frac{\partial^{2} u_{z}}{\partial z^{2}}), \frac{\partial u_{x}}{\partial x} + \frac{\partial u_{z}}{\partial z} = 0,

where $u_{x}$ , $u_{z}$ are liquid velocity projections on the coordinate axis, $ρ$ is the density of the liquid, $ν$ is the kinematic coefficient of the liquid viscosity, $p$ is the pressure.

The boundary conditions (the conditions of liquid and walls shifts velocities coincidence, as well, as the conditions for the liquid pressure at edges) are corresponded to the Eq. (2):

3

u_{x} = \partial u / \partial t, u_{z} = \partial w / \partial t, a t z = h {}_{0} / 2 + w,

u_{x} = 0, u_{z} = z_{m} d f (ω t) / d t, a t z = h {}_{0} / 2 + δ_{0} + z_{m} f (ω t),

4

p = p_{0}, a t x = \pm l,

where $u$ , $w$ are longitudinal movement and deflection plate laws.

The equation of the bending oscillations of the plate, resting on Pasternak foundation, can be written down, as in references [21, 25]:

5

D \frac{\partial^{4} w}{\partial x^{4}} + κ w - η \frac{\partial^{2} w}{\partial x^{2}} + ρ_{0} h_{0} \frac{\partial^{2} w}{\partial t^{2}} = - {q_{z z}^{}|}_{z = h_{0} / 2 + w} .

Here $w$ is the plate deflection, $D$ is the bending stiffness of plate, $ρ_{0}$ is the density of plate, $κ$ is the foundation normal stiffness, $η$ is the foundation shear coefficient, $q_{z z} = - p + 2 ρ ν \frac{\partial u_{z}}{\partial z}$ is the normal stress in a liquid layer [24].

Boundary conditions for Eq. (5) are the conditions of simply supported edges:

6

w = \partial^{2} w / \partial x^{2} = 0, a t x = \pm l .

Let us introduce dimensionless variables and small parameters into our consideration:

7

ξ = x / l, ζ = (z - 0,5 h_{0}) / δ_{0}, τ = ω t, u_{z} = w_{m}^{} ω U_{ζ}, u_{x} = (w_{m} ω / ψ) U_{ξ},

w = w_{m}^{} W, u = u_{m}^{} U, p = p_{0} + P ν ρ w_{m}^{} ω ψ^{- 2} / δ_{0}, λ = w_{m}^{} / δ_{0} ≪ 1,

ψ = δ_{0} / l ≪ 1 .

Taking into account Eq. (7), the hydrodynamic problem in dimensionless variables in zero approximation on $ψ$ and $λ$ will be written down, as:

8

\frac{\partial P}{\partial ξ} = \frac{\partial^{2} U_{ξ}}{\partial ζ^{2}}, \frac{\partial P}{\partial ζ} = 0, \frac{\partial U_{ξ}}{\partial ξ} + \frac{\partial U_{ζ}}{\partial ζ} = 0 .

With boundary conditions:

9

U_{ξ} = 0, U_{ζ} = (z_{m} / w_{m}) d f (τ) / d τ, a t ζ = 1, U_{ξ} = ψ (u_{m} / w_{m}) \partial U / \partial τ,

U_{ζ} = \partial W / \partial τ, a t ζ = 0, P = 0, a t ξ = \pm 1 .

The normal stress in the liquid layer in the variables Eq. (7) is written down, as:

10

q_{z z} = - p_{0} - \frac{ν ρ w_{m}^{} ω}{ψ^{2} δ_{0}} P .

Further, in the course of solving the problem of Eqs. (8)-(9), we will assume, that $u_{m} / w_{m} = O (1),$ i.e. we consider, that in boundary conditions Eq. (9) will be $U_{ξ} = ψ (u_{m} / w_{m}) \partial U / \partial τ = o (1)$ . As a result, we get:

11

U_{ξ} = \frac{ζ^{2} - ζ}{2} \frac{\partial P}{\partial ξ}, U_{ζ} = \frac{\partial W}{\partial τ} + (2 ζ^{3} - 3 ζ^{2}) (\frac{\partial W}{\partial τ} - \frac{z_{m}}{w_{m}} \frac{d f}{d τ}) .

As well, as the equations for the pressure:

12

\frac{\partial^{2} P}{\partial ξ^{2}} = - 12 (\frac{\partial W}{\partial τ} - \frac{z_{m}}{w_{m}} \frac{d f}{d τ}) .

By integrating Eq. (12) and satisfying the boundary conditions for the pressure Eq. (9), we find:

13

P = 6 (ξ^{2} - 1) \frac{z_{m}}{w_{m}} \frac{d f}{d τ} - 12 \int_{- 1}^{ξ} \int_{}^{} \partial W / \partial τ d ξ d ξ + 6 (ξ + 1) \int_{- 1}^{1} \int_{}^{} \partial W / \partial τ d ξ d ξ .

Taking into account the boundary conditions Eq. (6), we present the form of the plate elastic deflections as the series of Sturm-Liouville problem eigenfunctions:

14

w = w_{m}^{} W = w_{m}^{} \sum_{k = 1}^{\infty} (R_{k}^{0} + R_{k}^{} (τ)) c o s ((2 k - 1) π ξ / 2) .

Here $R_{k}^{} (τ)$ is the harmonic time function, $R_{k}^{0}$ is the constant.

As a result, dimensionless pressure Eq. (13) with consideration of the deflection chosen form Eq. (14), takes form of:

15

P = 12 \sum_{k = 1}^{\infty} [\frac{z_{m}}{w_{m}} \frac{d f}{d τ} \frac{4 (- 1)^{k}}{(2 k - 1) π} {(\frac{2}{(2 k - 1) π})}^{2} + {(\frac{2}{(2 k - 1) π})}^{2} \frac{d R_{k}}{d τ}] c o s \frac{2 k - 1}{2} π ξ .

By substituting Eq. (15) in the expression for the normal stress Eq. (10) and disintegrating the constant pressure $p_{0}$ in the series of Sturm-Liouville problem eigenfunctions, we get:

16

q_{z z} = p_{0} \sum_{k = 1}^{\infty} \frac{4 (- 1)^{k}}{(2 k - 1) π} c o s \frac{2 k - 1}{2} π ξ - \frac{ρ ν w_{m} ω}{δ_{0} ψ^{2}} [12 \sum_{k = 1}^{\infty} {(\frac{2}{(2 k - 1) π})}^{2} \frac{d R_{k}}{d τ} c o s \frac{2 k - 1}{2} π ξ + 12 \frac{z_{m}}{w_{m}} \frac{d f}{d τ} {\sum_{k = 1}^{\infty} \frac{4 (- 1)^{k}}{(2 k - 1) π} (\frac{2}{(2 k - 1) π})}^{2} c o s \frac{2 k - 1}{2} π ξ] .

Taking into account Eqs. (14), (16) we write down the plate dynamics equations in the form of:

17

(\frac{D}{l^{4}} {(\frac{(2 k - 1) π}{2})}^{4} + κ + \frac{η}{l^{2}} {(\frac{(2 k - 1) π}{2})}^{2}) w_{m} (R_{k}^{0} + R_{k}) + ρ_{0} h_{0} ω^{2} w_{m} \frac{d^{2} R_{k}}{d τ^{2}} + 12 \frac{ρ ν ω}{δ_{0} ψ^{2}} {(\frac{2}{(2 k - 1) π})}^{2} w_{m} \frac{d R_{k}}{d τ} = p_{0} \frac{4 (- 1)^{k}}{(2 k - 1) π} - 12 \frac{ρ ν ω}{δ_{0} ψ^{2}} \frac{4 (- 1)^{k}}{(2 k - 1) π} {(\frac{2}{(2 k - 1) π})}^{2} z_{m} \frac{d f}{d τ} .

Due to Eq. (17) linearity for the constant pressure component, we get the following expression:

18

w_{m} R_{k}^{0} = p_{0} \frac{4 (- 1)^{k}}{(2 k - 1) π} {(\frac{D}{l^{4}} {(\frac{(2 k - 1) π}{2})}^{4} + \frac{η}{l^{2}} {(\frac{(2 k - 1) π}{2})}^{2} + κ)}^{- 1} .

The solution of Eq. (17) for the stationary harmonic oscillations regime has the form of:

19

w_{m} R_{k}^{} = - z_{m} [\frac{K_{k}^{z} K_{k}^{w} ω^{2}}{({\tilde{D}}_{k} - ρ_{0} h_{0} ω^{2})^{2} + (K_{k}^{w} ω)^{2}} f (τ) + \frac{K_{k}^{z} ω ({\tilde{D}}_{k} - ρ_{0} h_{0} ω^{2})}{({\tilde{D}}_{k} - ρ_{0} h_{0} ω^{2})^{2} + (K_{k}^{w} ω)^{2}} \frac{d f (τ)}{d τ}],

{\tilde{D}}_{k} = \frac{D}{l^{4}} {(\frac{(2 k - 1) π}{2})}^{4} + \frac{η}{l^{2}} {(\frac{(2 k - 1) π}{2})}^{2} + κ, K_{k}^{z} = 12 \frac{ρ ν}{δ_{0} ψ^{2}} \frac{4 (- 1)^{k}}{(2 k - 1) π} {(\frac{2}{(2 k - 1) π})}^{2},

K_{k}^{w} = 12 \frac{ρ ν}{δ_{0} ψ^{2}} {(\frac{2}{(2 k - 1) π})}^{2} .

Finally, the law of the plate hydroelastic oscillations, caused by the stamp movement and with consideration of Eq. (18) and (19), takes the form:

20

w = \frac{p_{0} l^{4}}{D} \sum_{k = 1}^{\infty} \frac{4 (- 1)^{k}}{(2 k - 1) π} {({(\frac{(2 k - 1) π}{2})}^{4} + \frac{η l^{2}}{D} {(\frac{(2 k - 1) π}{2})}^{2} + \frac{κ l^{4}}{D})}^{- 1}

∙ \cos (\frac{2 k - 1}{2 l} π x) - z_{m} A (x, ω) s i n (ω t + φ (x, ω)),

A (x, ω) = \sqrt{C^{2} + B^{2}}, φ (x, ω) = a r c t g (B / C),

C = \sum_{k = 1}^{\infty} \frac{K_{k}^{z} K_{k}^{w} ω^{2}}{({\tilde{D}}_{k} - ρ_{0} h_{0} ω^{2})^{2} + (K_{k}^{w} ω)^{2}} c o s \frac{2 k - 1}{2 l} π x,

B = \sum_{k = 1}^{\infty} \frac{K_{k}^{z} ω ({\tilde{D}}_{k} - ρ_{0} h_{0} ω^{2})}{({\tilde{D}}_{k} - ρ_{0} h_{0} ω^{2})^{2} + (K_{k}^{w} ω)^{2}} c o s \frac{2 k - 1}{2 l} π x .

By substituting Eq. (19) in Eq. (15) and taking into account Eq. (7), the pressure in a liquid layer between the stamp and the plate can be written down as:

21

p = p_{0} + z_{m}^{} Π (x, ω) s i n (ω t + φ_{p} (x, ω)), Π (x, ω) = \sqrt{S^{2} + Q^{2},}

φ_{p} (x, ω) = a r c t g (Q / S), Q = \sum_{k = 1}^{\infty} K_{k}^{z} ω (1 - \frac{(K_{k}^{w} ω)^{2}}{({\tilde{D}}_{k} - ρ_{0} h_{0} ω^{2})^{2} + (K_{k}^{w} ω)^{2}}) c o s \frac{2 k - 1}{2 l} π x,

S = \sum_{k = 1}^{\infty} \frac{K_{k}^{w} K_{k}^{z} ω^{2} ({\tilde{D}}_{k} - ρ_{0} h_{0} ω^{2})}{({\tilde{D}}_{k} - ρ_{0} h_{0} ω^{2})^{2} + (K_{k}^{w} ω)^{2}} c o s \frac{2 k - 1}{2 l} π x .

4. Summary and conclusion

The obtained analytical solution of the problems allows making the following conclusions. The first component of the expression for the deflection Eq. (20) is conditioned by static pressure in liquid $p_{0}$ , the second component being a dynamic deflection, which is conditioned by the plate-stamp interaction through viscous liquid layer. The value of second deflection component is defined by the function $A (x, ω)$ , which may be considered as a frequency dependent amplitude sag distribution along the channel. The analogous remarks can be made in relation to the law of pressure change in the channel Eq. (21). The value of the second pressure component is defined by the function $Π (x, ω)$ , which is a frequency dependent amplitude distribution of dynamic pressure along the channel. The functions $φ (x, ω)$ , $φ_{p} (x, ω)$ are frequency dependent functions of the plate deflection phase shift distribution and the pressure phase shift distribution along the channel, correspondingly.

The investigation of the functions behavior depending on oscillations frequency allows studying dynamic processes in the considered oscillation system. The analysis of the obtained expression for the plate deflection Eq. (20) makes it possible to assume that the coefficients, defining Pasternak foundation reaction, will influence the plate static deflection, as well as deflection dynamic amplitude. Also, the transition from Pasternak foundation to Winkler one is possible in terms of the obtained solution, the coefficient of the foundation shift $η$ being zero. Thus, the obtained results can be used for modeling and analyzing hydroelastic oscillations of elastic elements of the constructions, resting on the foundations and interacting with viscous liquid.

References

Kubenko V. D., Pleskachevskii Yu. M., Starovoitov E. I., Leonenko D. V. Natural vibration of a sandwich beam on an elastic foundation. International Applied Mechanics, Vol. 42, Issue 5, 2006, p. 541-547.

Publisher
Starovoitov E. I., Leonenko D. V. Thermal impact on a circular sandwich plate on an elastic foundation. Mechanics of Solids, Vol. 47, Issue 1, 2012, p. 111-118.

Publisher
Starovoitov E. I., Leonenko D. V. Vibrations of circular composite plates on an elastic foundation under the action of local loads. Mechanics of Composite Materials, Vol. 52, Issue 5, 2016, p. 665-672.

Publisher
Pradhan M., Dash P. R., Pradhan P. K. Static and dynamic stability analysis of an asymmetric sandwich beam resting on a variable Pasternak foundation subjected to thermal gradient. Meccanica, Vol. 51, Issue 3, 2016, p. 725-739.

Publisher
Kerboua Y., Lakis, Thomas A. A. M., Marcouiller L. Vibration analysis of rectangular plates coupled with fluid. Applied Mathematical Modelling, Vol. 32, Issue 12, 2008, p. 2570-2586.

Publisher
Bochkarev S. A., Lekomtsev S. V., Matveenko V. P. Hydroelastic stability of a rectangular plate interacting with a layer of ideal flowing fluid. Fluid Dynamics, Vol. 51, Issue 6, 2016, p. 821-833.

Publisher
Avramov K. V., Strel’nikova E. A. Chaotic oscillations of plates interacting on both sides with a fluid flow. International Applied Mechanics, Vol. 50, Issue 3, 2014, p. 303-309.

Publisher
Önsay T. Effects of layer thickness on the vibration response of a plate-fluid layer system. Journal of Sound and Vibration, Vol. 163, 1993, p. 231-259.

Publisher
Ageev R. V., Mogilevich L. I., Popov V. S., Popova A. A., Kondratov D. V. Mathematical model of pulsating viscous liquid layer movement in a flat channel with elastically fixed wall. Applied Mathematical Sciences, Vol. 8, Issue 159, 2014, p. 7899-7908.

Publisher
Faria Cassio T., Inman Daniel J. Modeling energy transport in a cantilevered Euler-Bernoulli beam actively vibrating in Newtonian fluid. Mechanical Systems and Signal Processing, Vol. 45, 2014, p. 317-329.

Publisher
Mogilevich L. I., Popov V. S. Investigation of the interaction between a viscous incompressible fluid layer and walls of a channel formed by coaxial vibrating discs. Fluid Dynamics, Vol. 46, Issue 3, 2011, p. 375-388.

Publisher
Mogilevich L. I., Popov V. S., Popova A. A. Dynamics of interaction of elastic elements of a vibrating machine with the compressed liquid layer lying between them. Journal of Machinery Manufacture and Reliability, Vol. 39, Issue 4, 2010, p. 322-331.

Publisher
Akcabay D. T., Young Y. L. Hydroelastic response and energy harvesting potential of flexible piezoelectric beams in viscous flow. Physics of Fluids, 24, p. 5-2012.

Publisher
Ageev R. V., Kuznetsova E. L., Kulikov N. I., Mogilevich L. I., Popov V. S. Mathematical model of movement of a pulsing layer of viscous liquid in the channel with an elastic wall. PNRPU Mechanics Bulletin, Vol. 3, 2014, p. 17-35.

Publisher
Ageev R. V., Mogilevich L. I., Popov V. S. Vibrations of the walls of a slot channel with a viscous fluid formed by three-layer and solid disks. Journal of Machinery Manufacture and Reliability, Vol. 43, Issue 1, 2014, p. 1-8.

Publisher
Alekseev V. V., Indeitsev D. A., Mochalova Yu. A. Resonant oscillations of an elastic membrane on the bottom of a tank containing a heavy liquid. Technical Physics, Vol. 44, Issue 8, 1999, p. 903-907.

Publisher
Hosseini-Hashemi S., Karimi M., Hossein Rokni D. T. Hydroelastic vibration and buckling of rectangular Mindlin plates on Pasternak foundations under linearly varying in-plane loads. Soil Dynamics and Earthquake Engineering, Vol. 30, Issue 12, 2010, p. 1487-1499.

Publisher
Kutlu A., Ugurlu B., Omurtag M. H., Ergin A. Dynamic response of Mindlin plates resting on arbitrarily orthotropic Pasternak foundation and partially in contact with fluid. Ocean Engineering, Vol. 42, 2012, p. 112-125.

Publisher
Ugurlu B., Kutlu A., Ergin A., Omurtag M. H. Dynamics of a rectangular plate resting on an elastic foundation and partially in contact with a quiescent fluid. Journal of Sound and Vibration, Vol. 317, Issues 1-2, 2008, p. 308-328.

Publisher
Kuznetsova E. L., Mogilevich L. I., Popov V. S., Rabinsky L. N. Mathematical model of the plate on elastic foundation interacting with pulsating viscous liquid layer. Applied Mathematical Sciences, Vol. 10, Issue 23, 2016, p. 1101-1109.

Publisher
Mogilevich L. I., Popov V. S., Popova A. A., Christoforova A. V. Mathematical modeling of hydroelastic walls oscillations of the channel on Winkler foundation under vibrations. Vibroengineering Procedia, Vol. 8, 2016, p. 294-299.

Search CrossRef
Mogilevich L. I., Popov V. S., Popova A. A. Interaction dynamics of pulsating viscous liquid with the walls of the conduit on an elastic foundation. Journal of Machinery Manufacture and Reliability, Vol. 46, Issue 1, 2017, p. 12-19.

Publisher
Panovko Y. G., Gubanova I. I. Stability and Oscillations of Elastic Systems. Consultants Bureau Enterprises, Inc., New York, N.Y., 1965.

Search CrossRef
Loitsyanskii L. G. Mechanics of Liquids and Gases. Pergamon Press, Oxford, 1966.

Search CrossRef
Pasternak P. L. On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants. Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu i Architekture, Moscow, 1954 (in Russian).

Search CrossRef

Cited by

Proceedings of the 4th International Conference on Industrial Engineering

V. S. Popov | L. I. Mogilevich | E. D. Grushenkova

(2019)

About this article

Received

18 March 2017

Accepted

19 March 2017

Published

30 June 2017

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/vp.2017.18358

Keywords

hydroelastic oscillations

vibrating stamp

viscous liquid

plate

vibration

Pasternak foundation

Acknowledgements

The reported study was funded by Russian Foundation for Basic Research (RFBR) according to the Research Project No. 15-01-01604-a and President of Russian Federation Grant No. MD-6012.2016.8.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 11 18

Vibration and instability of a fluid-conveying nanotube resting on elastic foundation subjected to a magnetic field

Ming Li, Junru Zhou, Qian Deng, Liufei Lv

Research article

2020 03 31

Effects of foundation mass on dynamic responses of beams subjected to moving oscillators

T. Phuoc Nguyen, D. Trung Pham, P. Hoa Hoang

Research article

2019 09 30

Analytical solution of a vibrational problem for visco-elastic plate with Kelvin type boundary conditions

Ashish Kumar Sharma, Manoj Kumar Dhiman, Silky Bensal

Research article

2018 12 13

Analysis of free vibration of nano plate resting on Winkler foundation

Piyush Pratap Singh, Mohammad Sikandar Azam, Vinayak Ranjan

D. V. Kondratov, L. I. Mogilevich, V. S. Popov, and A. A. Popova, “Hydroelastic oscillation of a plate resting on Pasternak foundation,” Vibroengineering PROCEDIA, Vol. 12, pp. 102–108, Jun. 2017, https://doi.org/10.21595/vp.2017.18358

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2017.18358
UR  - https://doi.org/10.21595/vp.2017.18358
TI  - Hydroelastic oscillation of a plate resting on Pasternak foundation
T2  - Vibroengineering PROCEDIA
AU  - Kondratov, Dmitry V.
AU  - Mogilevich, Lev I.
AU  - Popov, Victor S.
AU  - Popova, Anna A.
PY  - 2017
DA  - 2017/06/30
PB  - JVE International Ltd.
SP  - 102-108
VL  - 12
SN  - 2345-0533
ER  - 

Copy Ris

Copied to clipboard!

@article{Kondratov_2017,
	doi = {10.21595/vp.2017.18358},
	url = {https://doi.org/10.21595/vp.2017.18358},
	year = 2017,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {12},
	pages = {102--108},
	author = {Dmitry V. Kondratov and Lev I. Mogilevich and Victor S. Popov and Anna A. Popova},
	title = {Hydroelastic oscillation of a plate resting on Pasternak foundation},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]D. V. Kondratov, L. I. Mogilevich, V. S. Popov, and A. A. Popova, “Hydroelastic oscillation of a plate resting on Pasternak foundation,” Vibroengineering PROCEDIA, vol. 12, pp. 102–108, Jun. 2017, doi: 10.21595/vp.2017.18358.

Copy IEEE

Copied to clipboard!

Kondratov, Dmitry V., Lev I. Mogilevich, Victor S. Popov, and Anna A. Popova. “Hydroelastic Oscillation of a Plate Resting on Pasternak Foundation.” Vibroengineering PROCEDIA 12 (June 30, 2017): 102–8. https://doi.org/10.21595/vp.2017.18358.

Copy Chicago

Copied to clipboard!

Hydroelastic oscillation of a plate resting on Pasternak foundation

Abstract

1. Introduction

2. Statement of the problem

3. The theory

4. Summary and conclusion

References

Cited by

About this article

Related Articles