Analytical solution of a vibrational problem for visco-elastic plate with Kelvin type boundary conditions

1. Introduction

Study in the field of vibration plays an important role in the branch of applied science and engineering. By vibration we mean a movement of the particle of an elastic or rigid body which repeats itself periodically. In the modern era, we cannot neglect the effect of vibrations as all engineering machines and structures produce vibrations. Since vibrations directly effects the life and work-power of the machine, therefore knowledge about the first few modes of vibration is essential and necessary to a mechanical engineer, before finalizing a design.

In these problems the thermal dependence of frequency on plates of different shapes are of great importance. In previous years, a lot of research has been done in the field of vibration of plates having different geometry such as orthotropic/isotropic, homogeneous/non-homogeneous and either considering or not considering the effect of temperature and thickness variation have been studied by number of authors. Transverse vibration analysis of rectangular plate having edges elastically against rotation and having two direction variations in thickness is discussed by Laura et al. [1]. Vibrational analysis of rectangle plate having thickness variation (linear and parabolic) along both the axes is studied by Gupta and Khanna [2, 3]. An effect of bi-directional exponential variation in thickness on vibrational modes using rectangle plate have described by Gupta et. al [4]. Lal and Dhanpati [5] have depicted the effect of non-homogeneity on vibration of orthotropic rectangular plates having varying thickness variation resting on Pasternak foundation. Effect of temperature, variation in Poisson ratio as non-homogeneity and simultaneous variation in density as well as in Poisson ratio to vibrational behavior of rectangular plate have described by Khanna and Kaur [6-8]. The transverse vibrations on simply supported plate with an oblique cut and generalized anisotropy have studied by Avalos and Laura [9]. Gupta and Singhal [10] studied parabolic thickness and temperature effect on vibrational frequencies of non-homogeneous rectangle plate.

The analysis of temperature dependent vibration of plate is very significant in the design of power plant turbines, nuclear reactors and other structure works at elevated temperature. In the industries the materials exposed to high temperature generally deviate from Hooke’s law and behaves visco-elastically. The elastic and viscous behavior of material depends mainly on frequency and temperature. Consequently, the vibration analysis has become very important from the point of view of designing a structure to be familiar in advance about its reaction. So that the essential measure to manage the structural vibrations and its amplitudes can be taken.

Rayleigh-Ritz method is used for the solution of equation of frequency corresponding to first two modes of vibration. A two terms deflection function has been used as a solution. Here, existing examination is to analysis the initial two vibration modes of rectangular geometry plate whose thermal effect and thickness change exponentially in $x$ and $y$ directions.

2. Differential equation of motion

The classical differential equation of motion for the transverse displacement $w$ of the rectangular plate is given by [1]:

and time function of plate is:

where $D_x=\frac{E_x{h}^3}{12(1-v_x{v}_y)}$, $D_y=\frac{E_y{h}^3}{12(1-v_x{v}_y)}$are flexural rigidity and $D_{xy}=\frac{G_{xy}{h}^3}{12}$ is torsional rigidity along $x$ and $y$ axis.

In mainstream of cases the impact of temperature is unobserved, yet they need to be taken into consideration. The motivation after this is that during heated up period’s structures are showing to high intensity heat fluxes and the material properties undergo significant changes hence the thermal effect on modulus of elasticity of material cannot be neglected. Most of engineering materials are found to have linear relationship between modulus of elasticity and temperature. Applications of such materials are due to lessening of weight and size, low operating cost and enhancement in efficiency and strength. So, we have considered two-dimensional temperature variations along $x$ and $y$-axis as [3]:

where:

Modulus of elasticity with time dependence is [3]:

On using temperature distribution along $x$ and $y$-axis in Eq. (4) as:

where $\alpha =\gamma {\tau }_0(0\le \alpha <1)$ is thermal gradient parameter.

Maximum strain energy $S_E$ and kinetic energy $K_E$ in cartesian coordinates are:

and:

where $D_1=v_x{D}_y\left(=v_y{D}_x\right)$. Now, assuming thickness $h$ varies exponentially along $x$ and $y$-axis as:

where $Z\left(x,y\right)=\left(e^{{\beta }_1\frac{x}{a}}\right)\left(e^{{\beta }_2\frac{y}{b}}\right)$, ${\beta }_1$ and ${\beta }_2$ are two taper constants.

3. Solution by Rayleigh-Ritz method

Rayleigh-Ritz method is applied for an appropriate deflection shape is selected and maximum strain and kinetic energy are equated. An equation in the following form is obtained as:

Now, Kelvin type boundary conditions for the geometry of plate shown are:

Appropriate deflection function in two terms for rectangular shape plate is [1]:

and $A_1$ and $A_2$ are to be calculate.

Now, unit less variables having no dimension are using for our convince as:

By using Eqs. (5), (8) and (12) in (6) and (7), we get:

where:

Substitute the value of $P_E$ and $K_E$ from Eqs. (13) and (14) in (9), we get:

where:

and:

where:

Eq. (16) contains two unknowns $C_1$ and $C_2$ comes after putting Eq. (11). $C_1$ and $C_2$ are to be determined from Eq. (16) as:

Simplify Eq. (19) we find the result as:

The determinant formed by the coefficient of Eq. (20) must vanish for non-zero solution be:

Eq. (21) gives a quadratic equation in $p^2$ and after solving one will get roots. On alter the value of $C_1=$ 1 in (11) one get $C_2=-Q_{11}$/$Q_{12}$ and Eq. (11) becomes:

4. Time function for vibration of plate

In general time function in Eq. (2) depends on $\check{D}$ and for Kelvin-Voigt model $\tilde{D}$ used as:

Now, visco-elastic constant $\eta$ and shear modulus $G$ taken with temperature dependence as that of Young’s moduli as:

On applying Eq. (3) in Eq. (24) with unit less term, one get:

where ${\alpha }_1$ and ${\alpha }_2=$ Thermal constants along $x$ and $y$-axis.

After using Eq. (23) in general time function Eq. (2), one gets differential equation of second order for time function $T$ as:

where:

On finding general solution Eq. (26), one gets solution in the form as:

where $a_1=-\frac{p^{2}k}{2}$ and $b_1=p\sqrt{1-{\left(\frac{pk}{2}\right)}^2}$ and $L_1$, $L_2$ are constant.

Assuming preliminary condition for finding the value of $L_1$ and $L_2$ as:

On putting preliminary condition in Eq. (28) it become:

Use result of Eq. (30) in Eq. (28), one get:

On using Eqs. (31) and (22) deflection function $W\left(x,y,t\right)=W\left(x,y\right)T\left(t\right)$, become:

Time period for the first two fundamental modes of vibration is given as:

Now, Logarithmic decrement for the first two fundamental modes of vibration is given as:

5. Result and discussion

Arithmetic result for first two fundamental modes of vibration with exponentially thickness and thermal effect variation are calculated with exactness with most modern computer tools i.e. MATLAB.

Calculation is done for logarithmic decrement ($^$), time period ($K$) and deflection ($w$) for various values of ${\beta }_1$ and ${\beta }_2$ and $a$/$b$ at various points for Ist and 2nd modes of vibrations. For calculations, the following material parameters of ‘Duralium’ which is an alloy of Aluminium, Copper, Magnesium and Manganese have been taken: $E=$ 7.08×10¹⁰N/M², $G=$ 2.632×10¹⁰ N/M², $\eta =$ 14.612×10⁵ Ns/M², $\rho =$ 2.80×10³ kg/M³, $v=$ 0.345, where $h_0$ is the thickness of the plate taken at the centre is $h_0=$ 0.01 mm.

Fig. 1. illustrates the result of $K$ (time period) for distinct value of $\alpha$ (thermal gradient) to 1st and 2nd modes of vibration. It is interesting to seen from figure that as $\alpha$ raises $K$ raises for 1st and 2nd modes of vibration.

Fig. 2. illustrates the result of $K$ (time period) for distinct value of $a$/$b=$ 1.5 (aspect ratio) to 1st and 2nd modes of vibration. It is interesting to seen from figure that as $a$/$b$ raises then $K$ fall for 1st and 2nd modes of vibration.

Fig. 1Vibration of time period K×10-5 with different values of thermal gradient α and aspect ratio a/b= 1.5

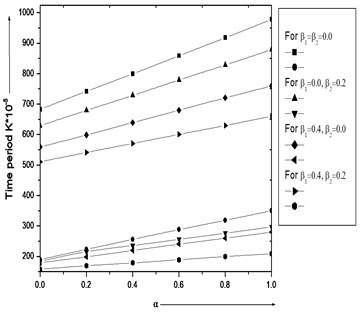
Fig. 2Vibration of time period K*10-5 with different values of aspect ratio (a/b)

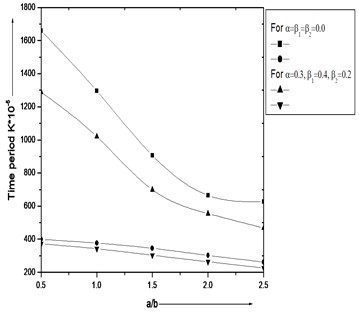
Fig. 3, 4. illustrates the result of $K$ (time period) for distinct value of ${\beta }_1$ and ${\beta }_2$ (taper constants) for 1st and 2nd modes of vibration. It is interesting to seen from figures that as ${\beta }_1$ and ${\beta }_2$ raises then time period fall for 1st and 2nd modes of vibration.

Fig. 5. illustrate the result of deflection $w$ for 1st and 2nd modes of vibration for $a$/$b=$ 1.5 (aspect ratio) with other distinct value: ${\beta }_1={\beta }_2=$ 0.0, $\alpha =$ 0.0, ${\alpha }_1=$ 0.2, ${\alpha }_2=$ 0.3, $Y=$ 0.6 and time = 0$K$ and 5$K$.

It is interesting to see that from figure as $a$/$b$ raises from 0.1 to 0.5 then deflection $w$ raises but as the value of aspect ratio raises from 0.5 to 1.0 then we clearly see that deflection $w$ fall for 1st and 2nd modes of vibration.

Fig. 6. illustrate the result of deflection $w$ for first two modes of vibration for aspect ratio $a$/$b=$ 1.5 with other different values: ${\beta }_1={\beta }_2=\alpha ={\alpha }_1={\alpha }_2=$ 0.0 and time = 0$K$ and 5$K$, $X=Y=$ 0.6.

Fig. 3Time period K*10-5 for various value of β1 and a/b= 1.5

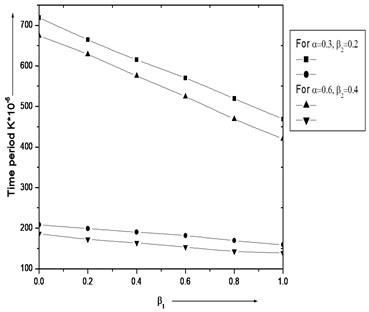
Fig. 4Variation of time period K*10-5 with different values of β2 and constant aspect ratio (a/b= 1.5)

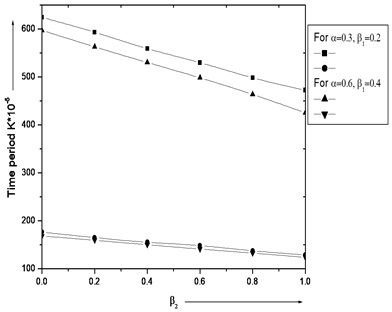
Fig. 5Deflection (w*10-5) for various value of X and Y, a/b= 1.5 and β1=β2= 0.0, α= 0.0, α1= 0.2, α2= 0.3, time = 0K and 5K

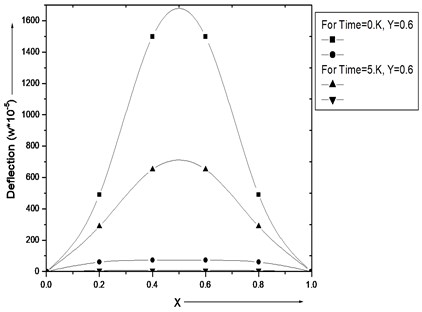
Fig. 6Deflection (w*10-5) for various value of a/b and β1=β2=α=α1=α2= 0.0

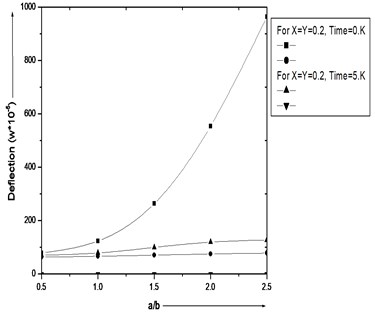
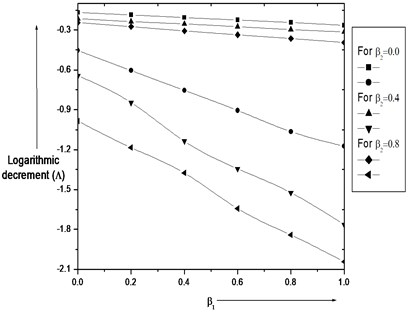
Fig. 7Logarithmic decrement (Λ) for various value of β1 and β2 and α=α1=α2= 0.0, a/b= 1.5

It is interesting to see that from the figure as aspect ratio raises then deflection raises for 1st and 2nd modes of vibration.

Fig. 7. illustrate result for $\mathrm{\Lambda }$ (logarithmic decrement) for $a$/$b$ (aspect ratio) various cases are deliberate for time period against taper constant, $a$/$b$ and $\alpha$ which are stated as below: $a$/$b=$ 1.5 for 1st and 2nd modes of vibration along distinct value of taper constants ${\beta }_1$. It is interesting to note that from figure as taper constant raises then logarithmic decrement fall for 1st and 2nd modes of vibration.

In above graphical data we can see that:

• Thermal gradient $\alpha$ increases, time period increases continuously.

• Aspect Ratio $a$/$b$ increases, time period decreases continuously.

• Taper constants (${\beta }_1$, ${\beta }_2$) increases, time period decreases continuously.

• $X$- increases, deflection show parabolic nature for different value of $X$.

• Aspect Ratio $a$/$b$ increases, deflection increases continuously.

• Taper constant ${\beta }_1$ increases, logarithmic decrement decreases.

6. Conclusions

This paper has devoted to study the effect of orthotropic tapered rectangular plate for first two fundamental frequencies based on classical plate theory. If thermal stresses are removed in the above case, the result match with the unheated plate in which temperature effect was not taken into account. After comparing with [5] authors conclude that as temperature effect introduced, time period and deflection increase gradually in comparison to unheated plate of varying thickness. Thus, engineers can find an alteration in the frequencies of a plate by a suitable selection of a variety of plate restriction measured at this time and accomplish their basic requirements.