Vibration and instability of a fluid-conveying nanotube resting on elastic foundation subjected to a magnetic field

Li, Ming; Zhou, Junru; Deng, Qian; Lv, Liufei

doi:10.21595/vp.2022.23006

Vibroengineering Procedia

Browse Procedia

Published: 18 November 2022

Check for updates

Vibration and instability of a fluid-conveying nanotube resting on elastic foundation subjected to a magnetic field

Ming Li¹

Junru Zhou²

Qian Deng³

Liufei Lv⁴

^{1, 2, 3, 4}College of Science, Wuhan University of Science and Technology, Wuhan, China

^{1, 2, 3, 4}Hubei Province Key Laboratory of Systems Science in Metallurgical Process (Wuhan University of Science and Technology), Wuhan, China

Corresponding Author:

Ming Li

Cite the article Download PDF

Downloads 276

Abstract

Using the nonlocal Euler-Bernouli beam model, this paper is carried out to investigate the vibrations and instability of a single-walled carbon nanotube (SWCNT) conveying fluid subjected to a longitudinal magnetic field. The nanobeam with clamped-clamped boundary conditions lies on the Pasternak foundation. Hamilton’s principle is applied to derive the fluid-structure interaction (FSI) governing equation and the corresponding boundary conditions. In the solution part the differential transformation method (DTM) is used to solve the differential equations of motion. The influences of nonlocal parameter, longitudinal magnetic field, Pasternak foundation on the critical divergence velocity of the nanotubes is studied.

1. Introduction

Micro and nanotube structural systems are widely used in biomedical applications, nanofiber composites, molecular drug delivery, and biosensors [1-2]. Experimental studies and molecular dynamics simulations have shown that small-scale effects have a significant impact on the properties of nanomaterials, but the classical continuum theory cannot accurately describe the mechanical behavior of such small-scale structures due to the lack of scale dependence, so a large number of continuum theories reflecting scale dependence have been proposed [3-4]. Among these, Eringen’s theory of nonlocal elasticity [5] has been successfully employed to examine a variety of static and dynamic mechanical behaviors of nanotubes. The fluid-conveying carbon nanotubes are commonly rested on a foundation, which could be simulated using the single-parameter Winkler foundation, the two-parameter Pasternak foundation, or several other viscoelastic foundation models [6-7]. Based on a nonlocal Euler-Bernouli beam model, Rafiei et al. [8] investigated the vibrational response of SWCNT conveying fluid resting on a viscoelastic Kelvin foundation. Recent research has revealed that the mechanical features of carbon nanotubes in an applied magnetic field and their magnetic properties have potential applications in the fields of nanosensors, spintronics, as well as micro- and nanoelectro mechanical systems [9-10]. For the chattering of fluid-conveying carbon nanotubes in an applied magnetic field, Ghane et al. [11] employed a nonlocal Timoshenko beam model to determine the impacts of magnetic field, flow velocityand small scale effect.

The above literature generally focuses on the analysis of the vibration properties of nanotubes when several parameters are coupled, however each parameter’s influence on other parameters is rarely discussed. In this paper, based on the nonlocal Euler-Bernouli beam model, the vibration characteristics of the fluid conveying carbon nanotube is investigated when the two-parameter Pasternak elastic foundation is coupled with the longitudinal magnetic field.

2. Vibration governing equation

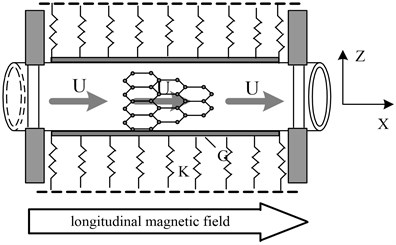
Fig. 1 shows a schematic diagram of a fluid conveying carbon nanotube subjected to a longitudinal magnetic field resting on the Pasternak foundation. The system only undergoes a small in-plane transverse vibration, gravity and the external pull and pressure of the tube are not taken into account, and the fluid inside the tube is an ideal fluid with constant flow velocity which is recorded as $U$ .

Fig. 1A fluid-conveyed SWCNT in Pasternak medium under the longitudinal magnetic field

Then, from the Euler-Bernoulli beam strain-displacement relationship we have:

1

ε_{X X} = - Z \frac{\partial^{2} W}{\partial X^{2}},

where $W (X, t)$ is the $Z$ -directional displacement, $t$ is the time, and $ε_{X X}$ is the strain in the $X$ -direction.

From the theory of nonlocal elasticity [9], the stress-strain relationship containing small-scale effects is:

2

σ_{X X} - {(e_{0} a)}^{2} \frac{\partial^{2} σ_{X X}}{\partial X^{2}} = E ε_{X X},

where $σ_{X X}$ is the stress in the $X$ -direction, $E$ is the nanotube elastic modulus, $e_{0}$ is the material constant, and $a$ is the material internal characteristic length.

The force acting on the nanotube by the fluid inside the nanotube can be expressed as [12]:

3

F_{f} = m_{f} (\frac{\partial^{2} W}{\partial t^{2}} + 2 U \frac{\partial^{2} W}{\partial X \partial t} + U^{2} \frac{\partial^{2} W}{\partial X^{2}}),

where $m_{f}$ is the mass of fluid inside the nanotube per unit length.

The Lorentz force per unit length acting on the nanotube is [9]:

4

F_{Z} = η A {H_{X}}^{2} \frac{\partial^{2} W}{\partial X^{2}},

where $A$ is the cross-sectional area of the pipe.

The force of the Pasternak elastic foundation on the nanotube is expressed as [6]:

5

F = K W - G \frac{\partial^{2} W}{\partial X^{2}},

where $K$ is the elastic spring and $G$ is the shear spring.

Based on the above equations, the work on the carbon nanotube by the elastic foundation, the magnetic field and the fluid inside the tube is:

6

W_{E x t} = \frac{1}{2} \int_{0}^{L} - (K W - G \frac{\partial^{2} W}{\partial X^{2}} + F_{Z} + F_{f}) W d X .

Applying Hamilton’s Principle:

7

\int_{t_{1}}^{t_{2}} δ (T_{p} - T_{k} - W_{E x t}) d t = 0,

where $T_{k}$ and $T_{p}$ are the total kinetic energy and strain energy of the nanotube system [4].

The system vibration differential equation can be obtained as:

8

\begin{array}{l} E I \frac{\partial^{4} W}{\partial X^{4}} + (m_{f} U^{2} - η A {H^{2}}_{X} - G) \frac{\partial^{2} W}{\partial X^{2}} + 2 m_{f} U \frac{\partial^{2} W}{\partial X \partial t} + K W + (m_{c} + m_{f}) \frac{\partial^{2} W}{\partial t^{2}} \\ - (e_{0} a)^{2} [\begin{matrix} (m_{f} U^{2} - η A {H^{2}}_{X} - G) \frac{\partial^{4} W}{\partial X^{4}} + 2 m_{f} U \frac{\partial^{4} W}{\partial X^{3} \partial t} \\ + K \frac{\partial^{2} W}{\partial X^{2}} + (m_{c} + m_{f}) \frac{\partial^{4} W}{\partial X^{2} \partial t^{2}} \end{matrix}] = 0, \end{array}

where $E I$ is the bending stiffness of SWCNT, $m_{c}$ is the mass of the nanotube per unit length.

The boundary conditions are:

9

X = 0, L : W = \frac{\partial W}{\partial X} = 0 .

3. Differential transformation method and solution methodology

Introduction of dimensionless variables and parameters:

w = \frac{W}{L}, x = \frac{X}{L}, τ = \sqrt{\frac{E I}{m_{c} + m_{f}}} \frac{t}{L^{2}}, β = \frac{m_{f}}{m_{c} + m_{f}},

u = U L \sqrt{\frac{m_{f}}{E I}}, μ = {(\frac{e_{0} a}{L})}^{2}, ψ = η A H_{X}^{2} \frac{L^{2}}{E I}, g = G \frac{L^{2}}{E I}, k = K \frac{L^{2}}{E I} .

The above Eq. (8) and the boundary condition Eq. (9) can be rewritten as the dimensionless equation:

10

\frac{\partial^{4} w}{\partial x^{4}} + (u^{2} - ψ - g) \frac{\partial^{2} w}{\partial x^{2}} + 2 u \sqrt{β} \frac{\partial^{2} w}{\partial x \partial τ} + k w + \frac{\partial^{2} w}{\partial τ^{2}} - μ [(u^{2} - ψ - g) \frac{\partial^{4} w}{\partial x^{4}} + 2 u \sqrt{β} \frac{\partial^{4} w}{\partial x^{3} \partial τ} + k \frac{\partial^{2} w}{\partial x^{2}} + \frac{\partial^{4} w}{\partial x^{2} \partial τ^{2}}] = 0,

with corresponding boundary conditions:

11

x = 0,1 : w = \frac{\partial w}{\partial x} = 0 .

Let the solution of Eq. (10) be $w = φ e^{Ω τ}$ , where $Ω$ is the dimensionless eigenvalue. Substituting the solution into Eq. (10) we have:

12

\frac{d^{4} φ}{d x^{4}} + (u^{2} - ψ - g) \frac{d^{2} φ}{d x^{2}} + 2 u \sqrt{β} Ω \frac{d φ}{d x} + (Ω^{2} + k) φ - μ [(u^{2} - ψ - g) \frac{d^{4} φ}{d x^{4}} + 2 u \sqrt{β} Ω \frac{d^{3} φ}{d x^{3}} + (Ω^{2} + k) \frac{d^{2} φ}{d x^{2}}] = 0 .

The differential transformation method (DTM) was used to solve the Eq. (12), then we have the differential transformation form of Eq. (12):

13

[1 - μ (u^{2} - ψ - g)] (n + 4)! Φ (n + 4) - 2 μ u \sqrt{β} Ω (n + 3)! Φ (n + 3)

+ [(u^{2} - ψ - g) - μ (Ω^{2} + k)] (n + 2)! Φ (n + 2) + 2 u \sqrt{β} Ω (n + 1)! Φ (n + 1)

+ (Ω^{2} + k) n! Φ (n) = 0 .

The DTM transformation of boundary conditions are given as follows:

14

Φ (0) = Φ (1) = 0,

15

\sum_{n = 0}^{\infty} Φ (n) = 0, \sum_{n = 0}^{\infty} n Φ (n) = 0 .

Let $F (2) = C_{1}$ , $F (3) = C_{2}$ , and substitute into Eq. (13) with Eq. (14), iterate to obtain $Φ (n)$ , $n =$ 4, 5,…, $N$ . Then, substituting $Φ (n)$ into Eq. (15), the following eigenvalue problem can be obtained:

16

[\begin{array}{l} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}] \{\begin{array}{l} C_{1} \\ C_{2} \end{array}\} = 0,

where $a_{i j}$ are functions of the dimensionless eigenvalue $Ω$ and other parameters. By calculating the determinant, the value of complax eigenvalues $Ω$ can be computed numerically. The real and imaginary parts of $Ω$ correspond to the damping and natural frequencies of the system, respectively. It should be mentioned that clamped-clamped nanotubes lose their stability by both imaginary and real parts of the first mode complax frequency are equal to zero.

4. Numerical results and discussion

The analytical parameters used in this paper are [9]: the density of the fluid $ρ_{f} =$ 1000 kg/m³, and that of the carbon nanotube $ρ_{c} =$ 2300 kg/m³, its outer layer radius $R_{0} =$ 3 nm, wall thickness $t_{d} =$ 0.1 nm, elastic modulus $E =$ 3.4 TPa. Poisson’s ratio $ν =$ 0.3. In vibration, the $L / 2 R_{0} =$ 40, the magnetic permeability is taken as $η =$ 4 $π$ ×10^-7 and $β =$ 0.5. The rest of the parameters are chosen in the examples, and the DTM algorithm is chosen an intercept number of 60.

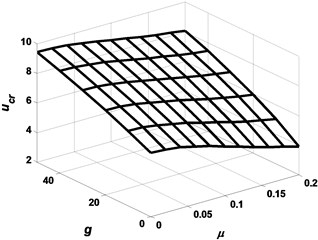
Figs. 2-3 present the critical flow velocity of the SWCNT conveying fluid as functions of coefficients of Pasternak foundation and magnetic field $H_{x}$ . Fig. 3 depicts that for different elasticity coefficients $k$ , the enhancement of the magnetic field can increase the critical flow velocity of the nanotube system and thus improve its stability. However, when comparing the enhancement values of the critical flow velocity by increasing the same magnetic field strength in detail, it can be found that the enhancement is different for different elasticity factors $k$ . This implies that the enhancement of the stability of the system by the magnetic field is suppressed to some extent with the increase of the elasticity coefficient $k$ . Similar conclusions can be obtained from the analysis of Fig. 4: the stability of the fluid-conveying carbon nanotube increases with the enhancement of the magnetic field for different shear coefficients $g$ . But the shear coefficient $g$ still suppresses the influence of the magnetic field on the stability of the system to some extent, although this suppression effect is not obvious, and the weaker the magnetic field the less obvious this effect is.

The effects of the elasticity coefficient $k$ and shear coefficient g on the critical flow velocity when considering the small-scale effect are presented in Figs. 4 and 5. As can be seen from Figs. 4 and 5, the increase in the nonlocal parameter with and without the elastic foundation reduces the stability of the system. A detailed comparison of the reduction in the dimensionless critical flow velocity, $Δ u_{c r}$ , for increasing the same nonlocal parameter $μ$ reveals that the shear coefficient $g$ suppresses the effect of the nonlocal parameter on the system stability, however, the elasticity coefficient $k$ amplifies the effect.

Fig. 2Critical flow velocities with longitudinal magnetic field in a fluid-conveying SWCNT for different values k (g=μ=0)

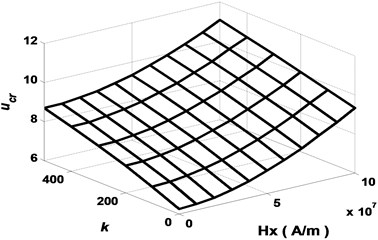
Fig. 3Critical flow velocities with longitudinal magnetic field in a fluid-conveying SWCNT for different values g (k=μ=0)

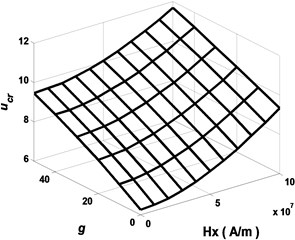
Fig. 4Critical flow velocities with nonlocal parameter μ in a fluid-conveying SWCNT for different values k (HX=g=0)

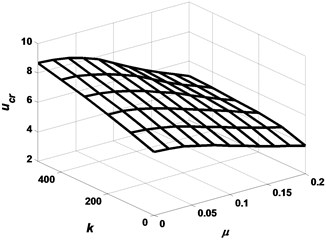
Fig. 5Critical flow velocities with nonlocal parameter μ in a fluid-conveying SWCNT for different values g (HX=k=0)

5. Conclusions

Size-dependent vibrations and instability of fluid-conveying SWCNT resting on a Pasternak elastic foundation were studied. The effects of different effective parameters, including magnetic field strength, two Pasternak coefficients and nonlocal parameter, were discussed in detail. And the paramount goal of this paper is to highlight the interaction of above paremeters effects on the instability behavior of the nanotube. The results demonstrate that the two Pasternak foundation reduce the magnetic field's influence on the stability of the system. However, the two coefficients of foundation have opposing impacts on the nonlocal parameter. Specifically, the elastic parameter increases the small-scale effect on the nanotube system while the shear parameter lowers it.

References

M. Malikan, “On the plastic buckling of curved carbon nanotubes,” Theoretical and Applied Mechanics Letters, Vol. 10, No. 1, pp. 46–56, Jan. 2020, https://doi.org/10.1016/j.taml.2020.01.004

Publisher
A. Amiri, R. Vesal, and R. Talebitooti, “Flexoelectric and surface effects on size-dependent flow-induced vibration and instability analysis of fluid-conveying nanotubes based on flexoelectricity beam model,” International Journal of Mechanical Sciences, Vol. 156, No. 6, pp. 474–485, Jun. 2019, https://doi.org/10.1016/j.ijmecsci.2019.04.018

Publisher
R. Ansari, R. Gholami, and A. Norouzzadeh, “Size-dependent thermo-mechanical vibration and instability of conveying fluid functionally graded nanoshells based on Mindlin’s strain gradient theory,” Thin-Walled Structures, Vol. 105, No. 8, pp. 172–184, Aug. 2016, https://doi.org/10.1016/j.tws.2016.04.009

Publisher
M. Li and K. Fang, “Vibration of elastic restrained simply supported carbon nanotubes,” Journal of Chongqing University, Vol. 43, No. 6, pp. 77–81, 2020.

Search CrossRef
A. C. Eringen, “Nonlocal polar elastic continua,” International Journal of Engineering Science, Vol. 10, No. 1, pp. 1–16, Jan. 1972, https://doi.org/10.1016/0020-7225(72)90070-5

Publisher
E. Ghavanloo, F. Daneshmand, and M. Rafiei, “Vibration and instability analysis of carbon nanotubes conveying fluid and resting on a linear viscoelastic winkler foundation,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 42, No. 9, pp. 2218–2224, Jul. 2010, https://doi.org/10.1016/j.physe.2010.04.024

Publisher
K. B. Mustapha and Z. W. Zhong, “The thermo-mechanical vibration of a single-walled carbon nanotube studied using the Bubnov-Galerkin method,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 43, No. 1, pp. 375–381, Nov. 2010, https://doi.org/10.1016/j.physe.2010.08.012

Publisher
M. Rafiei, S. R. Mohebpour, and F. Daneshmand, “Small-scale effect on the vibration of non-uniform carbon nanotubes conveying fluid and embedded in viscoelastic medium,” Physica E: Low-dimensional Systems and Nanostructures, Vol. 44, No. 7-8, pp. 1372–1379, Apr. 2012, https://doi.org/10.1016/j.physe.2012.02.021

Publisher
M. Li, L. F. Lv, H. S. Zheng, and K. Fang, “Magnetic field effect on flutter stability of a fluid-conveying cantilevered carbon nanotube under different temperature fields,” Chinese Journal of Solid Mechanics, Vol. 42, No. 1, pp. 87–93, 2021, https://doi.org/10.19636/j.cnki.cjsm42-1250/o3.2020.027

Publisher
Z. Lyu, Y. Yang, and H. Liu, “High-accuracy hull iteration method for uncertainty propagation in fluid-conveying carbon nanotube system under multi-physical fields,” Applied Mathematical Modelling, Vol. 79, No. 10, pp. 362–380, Mar. 2020, https://doi.org/10.1016/j.apm.2019.10.040

Publisher
M. Ghane, A. R. Saidi, and R. Bahaadini, “Vibration of fluid-conveying nanotubes subjected to magnetic field based on the thin-walled Timoshenko beam theory,” Applied Mathematical Modelling, Vol. 80, No. 11, pp. 65–83, Apr. 2020, https://doi.org/10.1016/j.apm.2019.11.034

Publisher
L. Wang and Q. Ni, “A reappraisal of the computational modelling of carbon nanotubes conveying viscous fluid,” Mechanics Research Communications, Vol. 36, No. 7, pp. 833–837, Oct. 2009, https://doi.org/10.1016/j.mechrescom.2009.05.003

Publisher

About this article

Received

20 October 2022

Accepted

04 November 2022

Published

18 November 2022

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2022.23006

Keywords

fluid-conveyed carbon nanotube

longitudinal magnetic field

Pasternak foundation

nonlocal parameter

differential transformation method

Acknowledgements

This research work has been supported by National Natural Science Foundation of China (Grant Nos. 51909196) and Hubei Province Key Laboratory of Systems Science in Metallurgical Process (Wuhan University of Science and Technology) of China (No. Y201520).

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2024 01 21

Research on estimation and control methods of natural frequency of irregular building structure vibration

Guicai Song

Research article

2022 10 18

Transient three-dimensional magnetohydrodynamic flow of heat and mass transfer of a Casson nanofluid past a stretching sheet with non-uniform heat source/sink, thermal radiation and chemical reaction

A. S. Odesola, I. O. Abiala, M. G. Sobamowo, O. J. Fenuga

Research article

2018 12 13

Analysis of free vibration of nano plate resting on Winkler foundation

Piyush Pratap Singh, Mohammad Sikandar Azam, Vinayak Ranjan

Research article

2016 12 31

Vibration and instability analysis of fluid-conveying nanotubes embedded in visco-elastic medium with consideration of surface effect

Ya-Xin Zhen

M. Li, J. Zhou, Q. Deng, and L. Lv, “Vibration and instability of a fluid-conveying nanotube resting on elastic foundation subjected to a magnetic field,” Vibroengineering PROCEDIA, Vol. 46, pp. 99–104, Nov. 2022, https://doi.org/10.21595/vp.2022.23006

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.23006
UR  - https://doi.org/10.21595/vp.2022.23006
TI  - Vibration and instability of a fluid-conveying nanotube resting on elastic foundation subjected to a magnetic field
T2  - Vibroengineering PROCEDIA
AU  - Li, Ming
AU  - Zhou, Junru
AU  - Deng, Qian
AU  - Lv, Liufei
PY  - 2022
DA  - 2022/11/18
PB  - JVE International Ltd.
SP  - 99-104
VL  - 46
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2022,
	doi = {10.21595/vp.2022.23006},
	url = {https://doi.org/10.21595/vp.2022.23006},
	year = 2022,
	month = {nov},
	publisher = {{JVE} International Ltd.},
	volume = {46},
	pages = {99--104},
	author = {Ming Li and Junru Zhou and Qian Deng and Liufei Lv},
	title = {Vibration and instability of a fluid-conveying nanotube resting on elastic foundation subjected to a magnetic field},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]M. Li, J. Zhou, Q. Deng, and L. Lv, “Vibration and instability of a fluid-conveying nanotube resting on elastic foundation subjected to a magnetic field,” Vibroengineering PROCEDIA, vol. 46, pp. 99–104, Nov. 2022, doi: 10.21595/vp.2022.23006.

Copy IEEE

Copied to clipboard!

Li, Ming, Junru Zhou, Qian Deng, and Liufei Lv. “Vibration and Instability of a Fluid-Conveying Nanotube Resting on Elastic Foundation Subjected to a Magnetic Field.” Vibroengineering PROCEDIA 46 (November 18, 2022): 99–104. https://doi.org/10.21595/vp.2022.23006.

Copy Chicago

Copied to clipboard!

Vibration and instability of a fluid-conveying nanotube resting on elastic foundation subjected to a magnetic field

Abstract

1. Introduction

2. Vibration governing equation

3. Differential transformation method and solution methodology

4. Numerical results and discussion

5. Conclusions

References

About this article

Related Articles