Model reaching adaptive-robust control law for vibration isolation systems with parametric uncertainty

1. Introduction

In the presence of parametric uncertainty, adaptive and robust control laws are used for control of uncertain systems. Some adaptive control laws for vibration isolation or active suspension systems are proposed in [1-4]. Model reference adaptive control law is used to follow the output of the ideal reference model [5]. Zuo et al. [6] proposed a model reaching adaptive control law to achieve a skyhook target without using a reference model. In [6], a dynamic manifold for the target dynamics is defined by using the states of the plant. Then, an adaptive control law is derived based on Lyapunov analysis to make the isolation system reach the dynamic manifold while estimating the unknown parameters. The Corless-Leitmann [7] approach is a popular approach used for designing robust controllers for dynamic systems. Some of robust control laws designed based on Corless-Leitmann [7] approach is introduced in [8-11].

In recent years, some researchers have studied about ride comfort and road handling. Florin et. all [12] analyzed, simulated the handling and ride performance of a quarter car model. Then, they compared the results with state space model and the transfer function. Ikenaga et al. [13] studied an active suspension system. They improved a control approach with a filtered feedback control scheme and an input decoupling transformation together for a full vehicle suspension system. Aggarwal [14] examined the magneto-rheological shock observer for semi-active quarter car system. And also, fuzzy logic controller has been used for actual damping force generation. These results show that the semi-active suspension system gives better results than passive suspension system. Sathishkumar et al. [15] study on modeling and simulation of a quarter vehicle model. They analyzed the results of the system by using MATLAB/SIMULINK. Chantranuwathana et al. [16] have applied the modular adaptive robust control (MARC) technique to design the force loop controller of an electro-hydraulic active suspension system. The importance of this controller is that the adaptation algorithm can be designed for explicit estimation convergence. Changizi et al. [17] studied application of fuzzy logic controller to damp automotive suspension system. They also used a PID control and a fuzzy logic controller together by using MATLAB simulation. Kaleemullah et al. [18] proposed an active suspension system for a quarter car using a robust H-infinity, a robust $H_2$, and a robust Mu-synthesis controller with passive suspension techniques. Parametric uncertainties were also modeled in the system. Sun et al. [19] presented a saturated adaptive robust control (ARC) strategy. Stability of the vehicle attitude and improvement of the ride comfort are achieved.

In this paper, a new approach, model reaching adaptive-robust control approach is studied. Based on the Lyapunov analysis and Corless-Leitmann approach [7], a new model reaching adaptive-robust control law is developed in order to make the uncertain system reach the ideal of a skyhook target model. The definition of the control law is based on the model reaching adaptive [6], robust [11] and robust-adaptive control laws [8, 9]. It is assumed that the system is uncertain and upper bound uncertainty is known. In previous studies [6], adaptive controller eliminates parameter uncertainties. However, adaptive-robust controller eliminates both parameter uncertainties and disturbances. The controller is applied to a vehicle suspension system and the ideal of a skyhook target without using a reference model is achieved. The results also show that the proposed adaptive-robust control law can increase the ride comfort of the vehicle active suspension system.

2. Model reaching adaptive control for vibration isolation

In the absence of friction force, the governing equation of an n-DOF isolated platform which is subject to excitation from vibration of the ground or base is given as follows [6]:

where $\mathbf{M}$, $\mathbf{C}$ and $\mathbf{K}$ are NxN dimensional mass, damping and stiffness matrices respectively. $\mathbf{B}$ indicates actuator displacement which is an NxR ($R$ ≥ $N$) matrix, $\mathbf{u}$ is the control force vector, $\mathbf{x}$ is the vector of vertical displacements and ${\mathbf{x}}_0$ is the vector of ground (road) disturbances.

Fig. 1a) Skyhook ideal representation, b) conventional representation [6]

a)

b)

The ideal skyhook dynamic equation is given as follows:

where $\stackrel{-}{\mathbf{M}}$, $\stackrel{-}{\mathbf{C}}$ and $\stackrel{-}{\mathbf{K}}$ are the mass, damping, and stiffness matrices respectively of any targeted dynamics. $\stackrel{-}{\mathbf{M}}$ is taken as unit mass and the ideal skyhook dynamics is:

Dynamic manifold is given as:

where $s$ is the Laplace operator. $\mathbf{L}\left(s\right)$ is a dynamic linear operator which affects system states to make system reaches any desired dynamics, $\mathbf{I}$ is identity matrix, $\mathbf{\sigma }$ denotes dynamic manifold which corresponds to desired dynamics by using the system states. On the manifold ($\mathbf{\sigma }=$ 0), then [6]:

And this equation is same as the target skyhook dynamic equation which is:

Unknown parameters in matrices $\mathbf{M}$, $\mathbf{C}$, $\mathbf{K}$ are arranged in a column vector as $\mathbf{a}$ and denoted as:

$\mathbf{Y}$ is a matrix formed by relative displacements and their velocities.

And $\mathbf{a}$ is a vector composed of unknown parameters and it can be written as follows:

The following Lyapunov function candidate is defined as [6]:

where $\tilde{\mathbf{a}}\left(t\right)$ denotes the error vector of on-line parameter estimations, $\mathbf{P}$ is a symmetric positive definite matrix. The time derivative of the Lyapunov function is:

From the Eqs. (1), (4) and (7), it can be obtained as:

The control-force vector is defined as [6]:

where the matrix ${\mathbf{k}}_d$ is a selected $N\times N$ positive-definite matrix composed of some control gains and ${\mathbf{k}}_d\mathbf{\sigma }\left(t\right)$ has PD controller action on the error, the vector $\widehat{\mathbf{a}}$ is the online estimation of the unknown parameters of $\mathbf{a}$, and the estimation error is $\tilde{\mathbf{a}}=\widehat{\mathbf{a}}-\mathbf{a}$. Substituting Eq. (13) into Eq. (12) yields:

If the adaptation law is chosen as [6]:

And:

Then $\dot{\mathbf{V}}\le \text{0}$ and the system is stable.

3. Derivation of the adaptive-robust control law

A novel model reaching robust control law is defined to derive the dynamics of the system to reach the manifold $\mathbf{\sigma }=$ 0 when the system parameters $\mathbf{M}$, $\mathbf{C}$ and $\mathbf{K}$ are unknowns. The parameters $\mathbf{M}$, $\mathbf{C}$, $\mathbf{K}$, $\mathbf{\sigma }$, $\mathbf{Y}$ and $\mathbf{a}$ are the same as it would be in the model reaching adaptive controller [6]. With these definitions, a nominal control input ${\mathbf{u}}_0$ is defined as:

where ${\mathbf{a}}_0$ is a vector composed of nominal parameters:

The definition of the nominal control law is similar to model reaching adaptive control law [6]. As a distinct from model reaching adaptive control law, ${\mathbf{a}}_0$ is fixed as it would be in the robust control law [11] and it is not updated in time as it would be in the model reaching adaptive control strategy [6]. Then, the control parameter is defined as in terms of nominal control law as follows:

where ${\mathbf{u}}_1$, ${\mathbf{u}}_2$ and ${\mathbf{u}}_3$ are additional control inputs. In order to show the stability of the system, the following theorem is proposed.

Theorem:

Let $\epsilon >0$. Considering the control law defined in Eq. (19), control inputs, ${\mathbf{u}}_1$, ${\mathbf{u}}_2$ and ${\mathbf{u}}_3$ are defined as:

where $\widehat{\mathbf{\pi }}$ is the estimation of parameters, $\widehat{\mathbf{\psi }}$ is the estimation of uncertainty bound of parameters, $\mathbf{\rho }$ is the uncertainty bound of parameters. The dynamics compensators $\widehat{\mathbf{\pi }}$ and $\widehat{\mathbf{\psi }}$ are defined as follows:

where $\mathbf{\beta }$, $\mathbf{\alpha }$ and $\mathbf{\lambda }\in R$ are adaptation gains. A new parameter error vector $\tilde{\mathbf{\Phi }}$ is defined as:

If the control inputs ${\mathbf{u}}_1$, ${\mathbf{u}}_2$ and ${\mathbf{u}}_3$ are substituted into the control law (19), then, the manifold $\mathbf{\sigma }$ will be ultimately bounded.

Proof:

In order to proof the theorem, the following Lyapunov function candidate is defined as:

The time derivative of the Lyapunov function is:

Substituting the Eq. (4) into Eq. (24) yields:

Then:

where:

As seen from Eq. (26), there are relationships between the control inputs ${\mathbf{u}}_1$, ${\mathbf{u}}_2$, ${\mathbf{u}}_3$ and the time dependent function ${\tilde{\mathbf{\Phi }}}^T\tilde{\mathbf{\Phi }}$. The time dependent function ${\tilde{\mathbf{\Phi }}}^T\tilde{\mathbf{\Phi }}$ is defined as [8]:

Then, ${\tilde{\mathrm{\Phi }}}^T\tilde{\mathrm{\Phi }}$ is obtained as:

Control parameters are defined in Eq. (20) such that ${\mathbf{u}}_2=-\widehat{\mathbf{\pi }}$, ${\mathbf{u}}_3=\widehat{\mathbf{\psi }}$. Substitution the Eq. (20) and Eq. (29) into Eq. (26), the following equation is obtained:

As seen from Eq. (30), the second and the third terms are canceled out by each other then, Eq. (30) is arranged as:

In this situation, two cases are considered.

Case 1: If $‖{\mathbf{Y}}^T\mathbf{\sigma }‖\rangle \mathbf{\epsilon }$:

Case 2: If $‖{\mathbf{Y}}^T\mathbf{\sigma }‖\le \mathbf{\epsilon }$

If $‖{\mathbf{Y}}^T\mathbf{\sigma }‖\le \mathbf{\epsilon }$, then ${\mathbf{u}}_2=-\mathbf{\rho }\frac{{\mathbf{Y}}^T\mathbf{\sigma }}{\mathbf{\epsilon }}$. The remaining terms of Eq. (31) are considered as:

The last term achieve maximum value of $\mathbf{\epsilon }\mathbf{\rho }$/4 when$‖{\mathbf{Y}}^T\mathbf{\sigma }‖=\mathbf{\epsilon }/\text{4}$. Thus, Eq. (33) would be:

Eq. (35) is similar to robust control law in [11] and the following equation is obtained for $\dot{\mathbf{V}}\le 0$:

where $‖\mathbf{\sigma }‖>w$ and $\delta$ min (${\mathbf{k}}_d$) is a minimum eigenvalue of ${\mathbf{k}}_d$.

4. Application to a vehicle suspension system

In order to investigate the performance of the proposed controller, the controller is applied to a quarter car vehicle model in Fig. 2.

Fig. 2Quarter vehicle model with controller

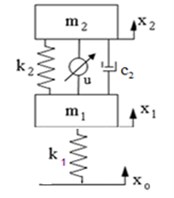
Equations of the vertical motion of the vehicle main body are as follows [16]:

where $x_2$ is the vertical displacement of vehicle main body, $x_1$ is the vertical displacement of tyre-axle mass, $x_0$ is the road disturbance, $u$ is the controller force. The other system parameters are given in Table 1.

If the vehicle carries unknown load and the load changes to $m_2+\mathrm{\Delta }{m}_2$, $k_2+\mathrm{\Delta }{k}_2$, $c_2+\mathrm{\Delta }{c}_2$. Considering the previous studies [20], uncertainties on the parameters are assumed as follows: 100 kg increase on the mass including passenger and luggage, a possible 10 % uncertainty on both stiffness and the damping of the suspension system. Hence, the controller is designed in the robustness of interval:

Considering the previous studies [11], mean value of the range of possible parameters are chosen nominal control parameters and they are given in Table 2.

With this choice of uncertainty parameters, the uncertainty bound is calculated as:

And thus $\rho =$ 1649.65. Uncertainty bound separately shown in Table 3.

Other control parameters used in the simulation are as follows:

Road disturbance is given in Fig. 3 [13].

Fig. 3Road disturbance [13]

The controller is applied to a vehicle suspension system and the results are given in Figs. 4-10.

As seen from the Fig. 4, the sprung mass acts as ideal skyhook model as it would be given in Eq. (3) in case of the vehicle is subjected to the road disturbance and if the system faces to parametric uncertainties. The amplitudes of the vertical displacement are significantly reduced to that of the targeted dynamics which oscillates around zero amplitude. The vehicle has reached the targeted dynamics with small error values. The peak value for vertical displacement of the controlled system is nearly 0 m while it is 0.095 m in passive system. There are two main goals here. On the first hand, the targeted dynamics should be reached. On the other hand, the vertical displacements should be minimized. Both goals are achieved in this study. One can obtain from here that the applied proposed adaptive-robust control law is successfully suppressed the vertical oscillations.

Fig. 4The oscillation of the sprung mass over time

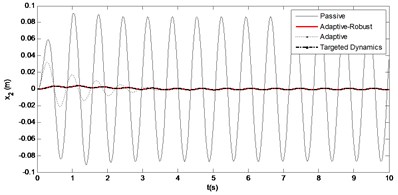
Fig. 5Dynamic manifold

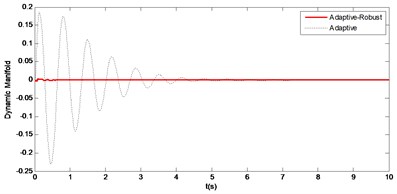
Fig. 6The vertical acceleration of sprung mass over time

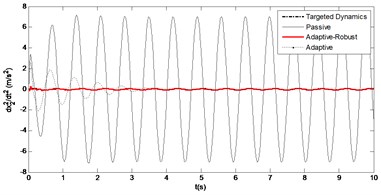
Fig. 7Suspension gap changes over time

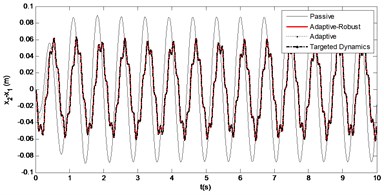
Fig. 8Controller force changes over time

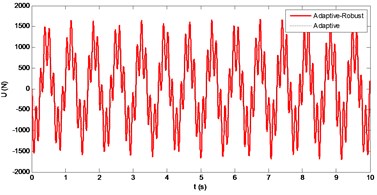
Fig. 9Frequency response of the vertical displacement

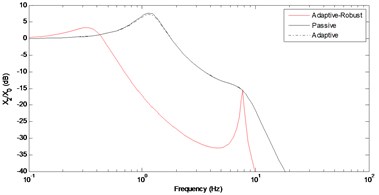
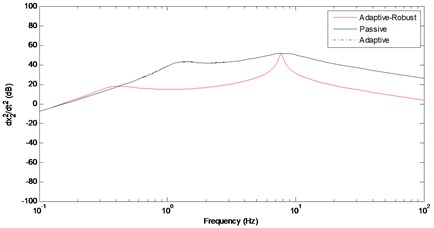
Fig. 10Frequency response of the vertical acceleration

In order to observe whether the vehicle’s vertical movement reached the targeted dynamics or not, Fig. 5 should be taken into consideration, as well. When the dynamic manifold (4) is zero, then it is said that the targeted ideal skyhook model (3) is reached. As it can be seen from the figure that sprung mass tracks the targeted dynamics with very small error. This value is sufficient.

The main criterion for a good ride comfort is to minimize the vertical acceleration as soon as possible. According to Newton’s second law, the acceleration causes the force that makes the human beings uncomfortable. It can be seen from the Fig. 6 that the acceleration is around the zero and it reaches the targeted dynamics acceleration values. The peak value of the acceleration in passive system is approximately 7.5 m/s² while it is nearly 0 m/s² in controlled system. This result shows that the ride comfort has been improved.

As seen from the Fig. 7, the suspension gap is decreased in active system by using the robust control law. The change of the controller force with respect to time is given in Fig. 8. The frequency responses of the vehicle main body and related acceleration are given in Figs. 9-10. As seen from the figures, the proposed controller is significantly reduced the resonance frequency of the main body. This indicates that the vehicle ride-comfort has been improved. However, there is an increase on the resonance frequency of the tyre-axle mass. Any increasing on the second peak shows that vehicle road handling is decreased while the ride-comfort is improved.

5. Conclusions

In this paper, a new approach, a new adaptive-robust model reaching control law is studied to achieve target dynamics (skyhook isolation) without reference model. Lyapunov Theory, based on the Corless-Leitmann approach [7] is used for designing the model reaching adaptive-robust control law and a uniform boundness of the manifold has been approved. The control law includes a new model reaching adaptive control and a new robust control algorithm. Development of a model reaching robust control law has not been considered before. The definition of the robust control law is similar to model reaching adaptive control law [6]. As a distinct from model reaching adaptive control law, nominal control parameters are fixed as it would be in the robust control law [11] and it is not updated in time as it would be in the model reaching adaptive control strategy [6]. In the model reaching adaptive control law, parameters and upper bounding functions are updated as a trigonometric function depending on the relative displacements, velocities and a defined manifold. Thus, according to the Lyapunov theorems, it has been concluded that when $\mathbf{t}\to \infty$ yields $\mathbf{\sigma }\to 0$. This result shows that the plant achieves the target dynamics of shyhook isolation. It is possible for the plant to achieve the target dynamics fast as a result of estimation of the most appropriate values of $\widehat{\mathbf{\pi }}$ and$\widehat{\mathbf{\psi }}$. As seen from the simulation results, the proposed adaptive-robust control law remarkably increases the ride comfort and decreases the motion of the main vehicle body. The numerical results also verify that the most appropriate theoretical values of the $\widehat{\mathbf{\pi }}$ and $\widehat{\mathbf{\psi }}$ can be estimated and the fast convergence of the plant to the target dynamics can be achieved. Application of this controller to a full vehicle system should be considered for a future study.