Optimization for heat and sound insulation of honeycomb sandwich panel in thermal environments

2.1. Heat transfer calculation method

In this paper, Swann and Pittman’s semi-empirical formula is used to analyze the thermal performance of aluminum honeycomb sandwich panels. Swann and Pittman ignore the temperature gradient of the skin and treat the heat transfer in the thickness direction of the sandwich panel as a one-dimensional linear problem. The equivalent thermal conductivity of honeycomb sandwich considering solid, gas heat conduction and radiant heat transfer is expressed as:

where $k_f$ and $k_g$ represent thermal conductivity of core and air, $∆A/A$ is the ratio of cell wall fraction to total cell area of the cross-sectional area of the honeycomb sandwich cell, $k_r$radiation equivalent thermal conductivity, the expression is:

where $\lambda$ is the ratio of the core height to the straight hexagonal circumscribed circle diameter, $\epsilon$ and $\sigma$ are surface panel emissivity and Stefan-Boltzmann constant, $T_1$ and $T_2$ are the temperature of the upper and lower panels. The equivalent thermal conductivity is related to the temperature of the upper and lower panels, therefore, the temperature of the lower panel can be calculated by repeated iterations.

2.2. Heat insulation numerical calculation

The size of the aluminum alloy honeycomb panels studied is as follows: the thickness of the upper and lower panels is 1 mm, the height of the honeycomb core is 20 mm, the wall thickness of the honeycomb core is 0.1 mm, and the length of the honeycomb unit is 5 mm. The emissivity of the honeycomb upper and lower plates is 0.25. The thermal physical properties of aluminum alloy are shown in Table 1. When the upper panel is subjected to a temperature of 300 ℃, the size effect of thermal insulation can be shown in Figs. 1-4.

Fig. 1The relationship between temperature difference and honeycomb wall thickness

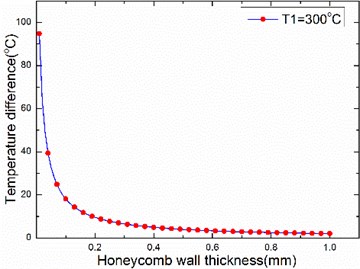
Fig. 2The relationship between temperature difference and length of honeycomb side

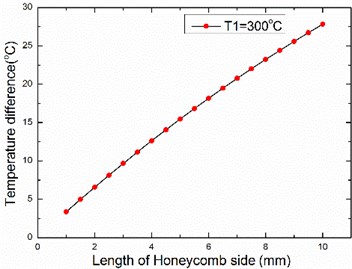
Fig. 3The relationship between temperature

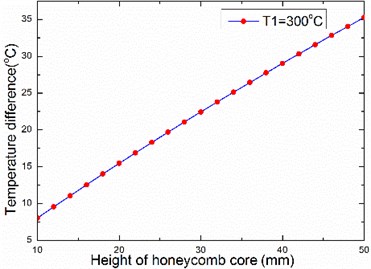
Fig. 4The relationship between temperature difference and thickness of panel

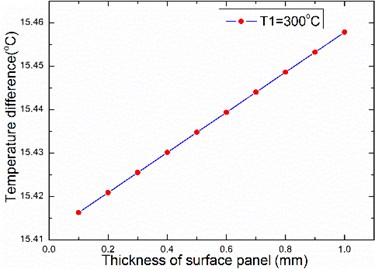
The thermal conductivity of air is much smaller than the thermal conductivity of aluminum alloy, the larger the volume ratio of the aluminum alloy structure in the honeycomb core layer, the better the heat transfer. Therefore, the larger the honeycomb wall thickness, the smaller the temperature difference; the temperature difference increases with the honeycomb side length, panel thickness and honeycomb core thickness, as illustrated in Figs. 2-4.

3.1. SEA theory

The modal density of structures depends on their boundary conditions and the governing equations of motion. For simply supported panels, the modal density is associated with the constant frequency loci of the wavenumber; then:

where $A_p$ is the surface of panel.

For honeycomb sandwich panels with stiff cores, the anti-symmetric motion is dominant in the frequency under consideration. The sixth-order governing equation for free motion of sandwich structures presented by Mead and Markus [8] can be written as:

with:

where $E_j$ is the Young’s modulus of the face sheet $j$; $G_c$ the out-of-plane shear modulus of the core; $t_j$ and $h$ are the thickness of the face sheet $j$ and the core, and $\mu$ the mass area density of sandwich panel.

A transmission model is considered to consist of three coupled systems as source room, panel and receiving room, with the subscripts are expressed as 1, 2 and 3. Hence, the transmission loss can be expressed as [6]:

with:

where $V_j$ is $T\left(K\right)$ the volume of source room and receiving room, ${\eta }_j$ and $n_j$ are the internal loss factor and modal density. ${\eta }_{rad}$is the coupling loss factor due to radiation damping, $R_{rad}$ is the radiation resistance of a baffled simply supported single-layer panel given by [9]. The internal loss factor of the sound field was determined from the reverberation time $T_3$, the modal density can be obtained from Eqs. (1-2).

3.2. Effect of temperature on acoustic performance

When only considering the effect of temperature on the physical parameters, a typical temperature-dependent material properties $P$ can be expressed as follows [10]:

where $H_i$ is the coefficients of temperature $T\left(K\right)$, which are particular to each specific material. Elastic modulus $E$ of aluminum alloy are taken as temperature dependent. The temperature-dependent coefficients are listed in Table 2.

Fig. 5The relationship between temperature and modal density of honeycomb sandwich panel

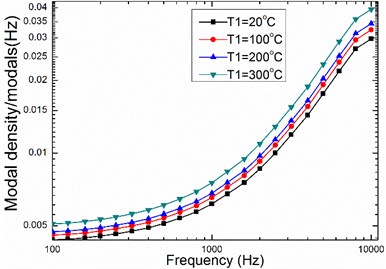
Fig. 6The relationship between temperature and sound transmission loss of honeycomb sandwich panel

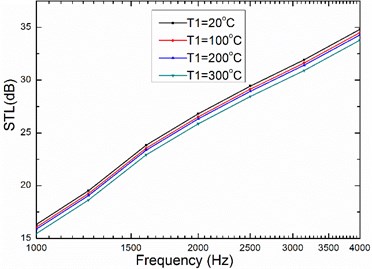
The dimensions of the panels are 0.84 m×0.42 m. $T_3$ and ${\eta }_2$ are set as 1.4 s and 0.03. Because the thickness of the upper and lower panels is very small, the temperature of upper and lower panels can be considered homogeneous. The temperature of honeycomb is assumed to be intermediate temperature of the core approximately. Modal density increases with temperature shown in Fig. 5, and increasing the temperature causes the sound transmission loss to decrease as illustrated in Fig. 6, the main reason is that the increase of temperature leads to the decrease of elastic modulus.

4.1. Objective function

The acoustical function is determined from a weighted average of the field-incidence transmission coefficients:

in which the weighting function is chosen to correspond to a weighting for seven frequencies in the range of 1000-4000 Hz [11]. Finally, the weighted sound transmission loss average was calculated from:

thermal insulation object function was set as:

In this paper, the constraint is the area mass density:

where ${\rho }_f$ and ${\rho }_c$ are the density of face panel and core. Therefore, Multi-objective optimization problem can be written:

where $w_1$ and $w_2$ denote the weight of objective function, satisfied with $w_1+w_2=$1. $AT{L}_0$ and $∆T_0$ were single objective optimization result of $ATL$ and $∆T$. ${\mu }_{max}=$4 kg/m² is used in the following numerical calculation.

4.2. Optimization

The SQP algorithm is an efficient method to solve the nonlinear programming problem. The basic idea is to construct a simple approximation optimization problem by using the information about the nonlinear programming problem. The current iteration point is corrected by solving it, with a series of linear programming or quadratic programming to successively approximate the original nonlinear programming problem.

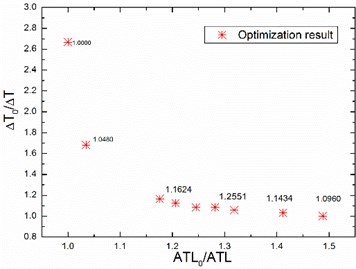
$AT{L}_0=$20.4951 dB and $∆T_0=$157.6101 °C are obtained by SQP, with constraint of area mass density. When $w_1$ and $w_2$ are set as 0.5, the iterative process of the multi-objective function value is shown in Fig. 7. The optimization results are achieved when the height of honeycomb core reaches a maximum, the relationship between ATL and $∆T$ is displayed in Fig. 8.

Fig. 7The iterative process of the multi-objective function value

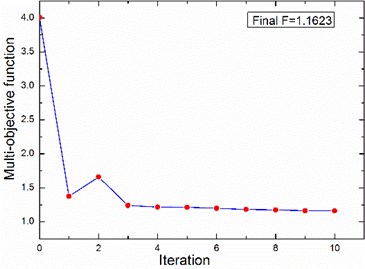
Fig. 8The relationship between ATL and ∆T