Sound insulation performance optimization of lightweight sandwich panels

Xu, Xiao-mei; Jiang, Yi-ping; Lee, Heow-pueh; Chen, Ning

doi:10.21595/jve.2016.16603

Journal of Vibroengineering

Browse Journal

Submit article

Published: 30 June 2016

Check for updates

Sound insulation performance optimization of lightweight sandwich panels

Xiao-mei Xu¹

Yi-ping Jiang²

Heow-pueh Lee³

Ning Chen⁴

^{1, 4}College of Automobile and Traffic Engineering, Nanjing Forestry University, Nanjing, China

²College of Engineering, Nanjing Agricultural University, Nanjing, China

^{3, 1}Department of Mechanical Engineering, National University of Singapore, Singapore, Singapore

Corresponding Author:

Xiao-mei Xu

Cite the article Download PDF

Downloads 1505

WoS Core Citations 8

CrossRef Citations 9

Abstract

Optimization of lightweight sandwich panels has been intensively studied, but optimization in terms of the acoustic objective is still a hot topic, and the influence on optimization results caused by sandwich panel geometric constraints is also rarely investigated. In this study, the optimization on lightweight sandwich panel designs is investigated by maximizing the sound insulation performance and minimizing the panel mass simultaneously. Firstly, the acoustic model of sandwich panels is discussed, which provides basic formulas to model the acoustic objective function. Secondly, the optimization problem is formulated as a bi-objective programming model, and a solution algorithm based on the non-dominated sorting genetic algorithm II (NSGA-II) is provided. Finally, the numerical experiments are carried out to verify the effectiveness of the proposed model and solution algorithm. Numerical results demonstrate the tradeoff between two objectives, the panel transmission loss corresponding to the three typical points in the Pareto front, and how the geometric constraints impact the optimization results for lightweight sandwich panels.

1. Introduction

Because of the advantage of high stiffness to mass ratio lightweight sandwich panels have been widely used in aerospace and automobile industries. However, due to the light weight, sandwich panels are easy to transmit and radiate noise, which gives rise to a serious vibro-acoustic problem in practical applications [1, 2]. To solve this problem, more and more researchers and practitioners are focusing on the acoustic performance optimization of lightweight sandwich panels.

For lightweight sandwich panels, acoustic performance optimization usually needs to consider the total panel mass and mechanical properties. The total panel mass, mechanical properties, and the sound insulation performance are essential criteria to measure the design of lightweight sandwich panels [3]. These design criteria are usually conflicting in real-world engineering applications and need to be balanced according to the practical considerations. Pioneering works in this field include single-objective optimization and multi-objective optimization. Among them the sound insulation performance of sandwich panels was treated as either the optimization objective or the constraint.

The acoustic objective optimization for lightweight sandwich panels has been investigated in a few literatures. In the reported studies sound insulation performance was usually evaluated by sound transmission loss (TL). Makris et al. addressed the comparison of different optimization techniques to find the optimum TL of sandwich panels [4], and then carried out the multi-objective optimization of sandwich panels considering four optimization objectives, namely TL, cost, panel end-loading, and mid-span deflection [3]. Lang and Dym [5] took the averaged TL over the frequency range 1000-4000 Hz as the objective function and carried out the acoustic performance optimization of sandwich panels. Thamburaj and Sun [6] considered the optimization problem on sound insulation performance of anisotropic sandwich beams. Zhou et al. [2] presented a bi-objective optimization model regarding double-walled panel by taking account of minimizing the weight and maximizing the acoustic transmission loss, and then illustrated the tradeoff between the two objectives via Pareto curve. Cameron et al. [7] proposed an optimal design model with respect to the multi-functional load bearing vehicle body panel and explored the compromising solutions between the structural and acoustic performance. Leite et al. [8] developed a multi-objective optimization model to optimize a classical sandwich panel with foam core, with the objectives of mass, flexural stiffness, and acoustic insulation performance, and then adopted genetic algorithm to obtain the Pareto optimal solutions.

On the other hand, sound insulation performance in previous literatures is also treated as a constraint in the optimization model of sandwich panels. Wennhage [9-11] investigated the minimum mass problem of sandwich panels by taking account of the acoustic and structural constraints. Wang [12] performed an optimization study on sandwich panels by considering the balance of acoustic and mechanical properties at the minimum weight. In the work conducted by Guerich et al. [13], TL of the sandwich panel was regarded as a constraint and the panel mass was adopted as the optimization objective.

Generally, in recent years multi-objective optimization of sandwich panels has gained more and more attentions, and the acoustic objective is still a challenge to be optimized because of the extremely complicated objective function [13]. Therefore, in the reported studies the sound insulation requirements for sandwich panels were usually treated as a constraint or a single objective so as to reduce the computational complexity. Although a few works have incorporated the acoustic objective into the multi-objective optimization model, the numerical exhibition on the complete distribution of Pareto optimal solutions is still an intractable issue [2, 14]. Moreover, the influence of geometric constraints on the optimization results of sandwich panels is also rarely investigated in the reported studies.

The motivations and contributions in this study contain three aspects. The primary purpose is to maximize the sound insulation performance of lightweight sandwich panels, and in the meantime, to minimize the total panel mass. The second goal is to unveil the complete distribution of Pareto optimal solutions between the sound insulation performance and the panel mass through introducing the solution algorithm based on the non-dominated sorting genetic algorithm II (NSGA-II). The last aim of this study is to shed new light on intriguing studies that reveal how geometric constraints affect the optimization results of sandwich panels in real-world engineering designs.

The remainder of this paper is organized as follows. In Section 2, the theoretical formulation of the present study is given, which consists of the acoustic model of sandwich panels, the bi-objective optimization model and the solution algorithm NSGA-II. In Section 3, the numerical experiments are demonstrated and the numerical results are analyzed. Finally, the concluding remarks and the highlighting direction for future work are provided in Section 4.

2. Theoretical formulation

2.1. Acoustic model of sandwich panels

In this part the acoustic model of sandwich panels is introduced, so as to provide a quantified measurement on sound insulation performance which used in the sandwich panel optimization model in subsection 2.2.1. TL is a critical criterion to measure the sound insulation performance of panels and it is usually affected by the sound wave frequency, the panel thickness and materials. On one hand, these factors make the acoustic analysis of sandwich panels more challenging. On the other hand, they also offer additional possibilities to tailor the acoustic properties in actual applications. This study formulates the acoustic model of sandwich panels based on the pioneering works in [15] and [16].

A typical structure of the sandwich panel is demonstrated in Fig. 1. In the figure, $x$ and $z$ denote the coordinates along the panel length and the panel thickness, respectively. $u$ and $w$ represent the displacements in the $x$ and $z$ directions, respectively. $ρ$ , $E$ and $t$ represent the material mass density, Young’s modulus, and the component thickness, respectively. The subscripts 1, 2 and $c$ denote the face sheet 1, face sheet 2, and the sandwich core, respectively. Moreover, all sound waves in the figure are assumed to be plane waves.

Fig. 1Geometry and material properties of a sandwich panel and the transmission of sound waves

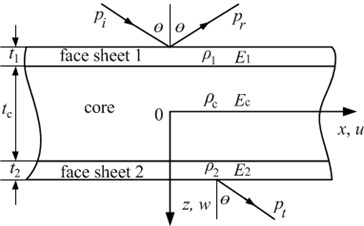
Let a pressure wave be incident on face sheet 1 at an angle $θ$ . The acoustic load $p_{1}$ on face sheet 1 is composed of incident pressure $p_{i}$ , reflected pressure $p_{r}$ , and radiated pressure $p_{r a d 1}$ caused by the motion of face sheet 1. However, the acoustic load $p_{2}$ on face sheet 2 is only subject to radiated pressure $p_{r a d 2}$ , i.e., transmitted sound pressure $p_{t}$ .

The panel impedance is usually defined as the ratio between the pressure acting on the surface of panel and the vertical velocity of this surface [17]. Thus, the symmetric and anti-symmetric impedances of a sandwich panel can be expressed in Eq. (1) and Eq. (2):

1

Z_{s} = - \frac{p_{1} + p_{2}}{\dot{ω_{s}}} = - \frac{p_{1} + p_{2}}{i ω ω_{s}},

2

Z_{a} = \frac{p_{1} - p_{2}}{\dot{ω_{a}}} = \frac{p_{1} - p_{2}}{i ω ω_{a}},

where $\dot{ω_{s}}$ , $ω_{s}$ and ${\dot{ω}}_{a}$ , $ω_{a}$ represent the vertical velocities and displacements of the panel symmetric and anti-symmetric motions, respectively; $i$ is the imaginary unit; $ω$ is the circular frequency of sound waves.

According to the definition of sound transmission coefficient, the symmetric sandwich panel with identical face sheets can be evaluated by Eq. (3) [16]:

3

τ (θ, φ) = {|\frac{p_{t}}{p_{i}}|}^{2} = {|\frac{1}{1 + \frac{Z_{s}}{2 Z_{a i r}^{'}}} - \frac{1}{1 + \frac{Z_{a}}{2 Z_{a i r}^{'}}}|}^{2},

in which, $Z_{a i r}^{'} = Z_{a i r} / \cos θ = ρ_{a i r} c_{a i r} / \cos θ$ , where $z_{a i r}$ , $ρ_{a i r}$ and $c_{a i r}$ denote the acoustic impedance of air, the air mass density and the sound speed in air, respectively; $φ$ is the azimuthal angle.

In the case of a diffuse sound field, the incident angles are usually assumed to be uniformly distributed over a range [0, $θ_{l i m}$ ], where $θ_{l i m}$ is an empirical upper bound of the incident angle and is usually set as 78°. Then, the average of the sound transmission coefficient $\hat{τ}$ over all possible angles of incidence is obtained by integrating over the range of incident angle [18]:

4

\hat{τ} = \frac{\int_{0}^{2 π} \int_{0}^{θ_{l i m}} τ (θ, φ) \sin θ \cos θ d θ d φ}{\int_{0}^{2 π} \int_{0}^{θ_{l i m}} \sin θ \cos θ d θ d φ} .

The integration in Eq. (4) is carried out numerically by using the Simpson’s rule. According to [19], the random incidence TL is obtained by Eq. (5):

5

T L = 10 {log}_{10} |\frac{1}{\hat{τ}}| .

Obviously, $T L$ is frequency-dependent and its computation is very complicated. Eq. (4) and Eq. (5) provide basic formulas to model the acoustic objective function discussed in subsection 2.2.1.

2.2. Optimization model formulation

In this part, a bi-objective optimization model of lightweight sandwich panel is proposed, with the objective of maximizing the sound insulation performance and minimizing panel total mass. The face sheet thickness and the core thickness are chosen as the decision variables.

2.2.1. Objective function

2.2.1.1. Acoustic objective

The acoustic performance is an important criterion to measure the design of lightweight sandwich panels in practice. As pointed out by Makris et al. [4], there are mainly two kinds of quantitative approaches to evaluate the panel acoustic performance in the optimization literature, i.e., maximizing the weighted transmission loss average (TLA) of a sandwich panel over a frequency range, and keeping the sound transmission coefficient $\hat{τ}$ values at a collection of frequencies under the sound transmission class (STC) curves. In this study, maximizing the weighted TLA of a sandwich panel over the frequency range 1000-4000 Hz is adopted to formulate the acoustic objective so as to reduce the computational complexity. Specifically, the weighted transmission loss average (TLA) in seven discrete frequency points within the range 1000-4000 Hz is used as the measurement to quantify the panel acoustic performance. The weighting scale used here is actually the A-weighting scale for this frequency range, which is shown in Table 1. According to STC, the following seven discrete frequencies are considered: 1000, 1250, 1600, 2000, 2500, 3150, and 4000 Hz [4].

Table 1Normalized weights using the A-weighting [4]

Frequency Hz	A-weighting dB(A)	Multiplier 10^dB(A)/10	Normalized weights
1000	0	1.000	0.1156
1250	+0.6	1.148	0.1327
1600	+1.0	1.259	0.1455
2000	+1.2	1.318	0.1524
2500	+1.3	1.349	0.1559
3150	+1.2	1.318	0.1524
4000	+1.0	1.259	0.1455
			$\bar{1.0000}$

The weighted average of the sound transmission coefficient ${\hat{τ}}_{a v e}$ can be written as Eq. (6):

6

{\hat{τ}}_{a v e} = \sum_{i = 1}^{7} ω_{i} {\hat{τ}}_{i},

where $ω_{i}$ represents a normalized weight assigned to seven different points of frequency, as given in Table 1.

According to Eq. (5) and Eq. (6), the weighted TLA can be expressed as Eq. (7):

7

T L A = 10 {log}_{10} |\frac{1}{{\hat{τ}}_{a v e}}| .

For the sake of standardization, the acoustic objective function ${o b j}_{1}$ is defined as the inverse of TLA given in Eq. (7) and be written as Eq. (8):

8

{o b j}_{1} = \frac{1}{T L A} .

It is obvious that the higher the value of TLA, the better the sound insulation performance of panels. Therefore, ${o b j}_{1}$ should be minimized so as to improve the sound insulation performance of lightweight sandwich panels.

2.2.1.2. Mass objective

For lightweight sandwich panels, minimizing the total panel mass per unit area is chosen as the mass objective. Since symmetric sandwich panels exhibit higher TL than asymmetric ones at the equivalent mass [20], only symmetric sandwich panels are considered in this paper.

The properties of symmetric sandwich panels are $ρ_{1} = ρ_{2} = ρ_{f}$ , $t_{1} = t_{2} = t_{f}$ and $E_{1} = E_{2} = E_{f}$ , where $ρ_{f}$ , $t_{f}$ and $E_{f}$ denote the material density, thickness and Young’s modulus of the face sheet, respectively. Then the mass objective function of sandwich panel can be written as Eq. (9):

9

{o b j}_{2} = 2 ρ_{f} t_{f} + ρ_{c} t_{c} .

It is obvious that ${o b j}_{2}$ should be minimized so as to reduce the total sandwich panel mass.

2.2.2. Constraints

In the present study, the constraints mainly include the geometric constraints and the mechanical constraint. Geometric constraints of sandwich panels focus on the thickness constraints of the face sheet and the sandwich core, which can be given by Eq. (10):

10

\{\begin{matrix} {L_{f} \leq t}_{f} \leq U_{f}, \\ {L_{c} \leq t}_{c} \leq U_{c}, \end{matrix}

where, $L_{f}$ and $U_{f}$ denote the lower and upper bound of the face sheet thickness, respectively; $L_{c}$ and $U_{c}$ denote the lower and upper bound of the core thickness, respectively.

A simple mechanical constraint is adopted herein by considering the maximal deflection of a simply-supported 1 m×1 m square sandwich panel under 1 N force at the center of the panel [12]. According to [21], the deflection $δ$ at the center of the sandwich panel can be expressed as:

11

δ = \frac{F l^{3}}{24 E_{f} b t_{f} d^{2}} + \frac{F l t_{c}}{4 G_{c} b d^{2}},

where $F$ denotes the force at the center of the sandwich panel, $b$ and $l$ respectively denote the width and length of the sandwich panel, $E_{f}$ represents the Young’s modulus of the face sheets, $G_{c}$ represents the shear modulus of the core, $t_{f}$ and $t_{c}$ are respectively the thickness of the face sheet and the core, and $d = (t_{f} + t_{c})$ . Therefore, the mechanical constraint can be given by Eq. (12):

12

δ \leq δ_{0},

in which, $δ_{0}$ is the upper bound of the deflection at the center of the sandwich panel and its value can be chosen for different applications.

In summary, the bi-objective optimization model of lightweight sandwich panel discussed in this study can be stated as Eq. (13):

13

M i n {o b j}_{1} & {o b j}_{2},

s.t.   Eq. (10) and Eq. (12) .

2.2.3. Complexity analysis

According to Eq. (4) and Eq. (5), the formulation of TL is a non-convex function [22], which makes the TLA function in Eq. (7) non-convex. Therefore, the ${o b j}_{1}$ formulated in Eq. (8) is naturally a non-convex function. In addition, according to the formulation in Eq. (9), ${o b j}_{2}$ is a linear function. Besides, the geometric constraints in Eq. (11) are linear, and the mechanical constraint in Eq. (12) is non-convex [22]. Therefore, the proposed model Eq. (13) is a non-convex bi-objective programming.

The non-convex property of model Eq. (13) makes the traditional optimization approaches failed to find the global optimal solution [23]. In practical industrial applications, there are plenty of non-convex optimization problem. For these complicated problems, to find a feasible solution in a short time is more important than to find a global solution in a long computational time. Fortunately, the evolutional algorithm provides a very useful solution methodology to find a feasible and satisfactory solution [24].

2.3. Solution algorithm

The NSGA-II solution procedures for the proposed optimization model in Eq. (13) are demonstrated in this part. As an improved version of NSGA, NSGA-II links the elitism mechanism into NSGA and has a better sorting performance in solving the complicated multi-objective optimization problems [25]. NSGA-II proposes a new selection technique, called crowded tournament selection, where selection is done based on crowding distance (representing the neighborhood density of a solution). To implement elitism, the parent and child population are combined and the non-dominated individuals from the combined population are propagated to the next generation. Due to these advantages, NSGA-II has been widely adopted to assist the optimal design in many engineering areas [26, 27]. The following are main implementation procedures of NSGA-II to solve the proposed model in the study:

Step 1: Initialize the population size $N$ , the generation number $K$ , the crossover probability and the mutation probability.

Step 2: Generate an initial population denoted as $P$ with size $N$ randomly, in terms of the problem constraints Eq. (10) and Eq. (12).

Step 3: Evaluate each solution in the population by computing the values of objective functions ${o b j}_{1}$ and ${o b j}_{2}$ .

Step 4: Rank the solutions in the current population $P$ using non-dominated sorting and compute the crowding distance.

Step 5: Perform selection using the binary tournament selection operator and select the parents denoted as $P_{1}$ with size $N /$ 2 from the current population $P$ .

Step 6: Perform crossover and mutation (as in conventional genetic algorithm) to generate the offspring population denoted as $P_{2}$ from parents $P_{1}$ .

Step 7: Combine the current population $P$ and the current offsprings $P_{2}$ , i.e., $P \cup P_{2}$ .

Step 8: Replace the current population by the top $N$ individuals of the combined population.

Step 9: Check the termination condition. If the generation number $K$ has not been reached, the procedure would go to Step 5. Otherwise, the execution of the algorithm would end and the non-dominated solutions at the last generation would be obtained.

3. Numerical experiments

In order to verify the effectiveness of the proposed bi-objective optimization model and the solution algorithm, numerical experiments of a lightweight sandwich panel are carried out in this section. The effects of geometric constraints on the optimization results are also investigated.

3.1. Experimental settings

In this study, aluminum is adopted as the face sheet material of the lightweight sandwich panel and the polymer foam Rohacell 31 is chosen as the core material. The material properties of aluminum are $ρ_{f} =$ 2700 kg/m³, $E_{f} =$ 70 GPa, Poisson’s ratio $σ_{f} =$ 0.33. The core material properties are $ρ_{c} =$ 32 kg/m³, $E_{c} =$ 36 MPa, and the shear modulus $G_{c} =$ 13 MPa. Herein, the loss factors of aluminum and polymer foam Rohacell 31 are assumed to be 0.01 and 0.03, respectively.

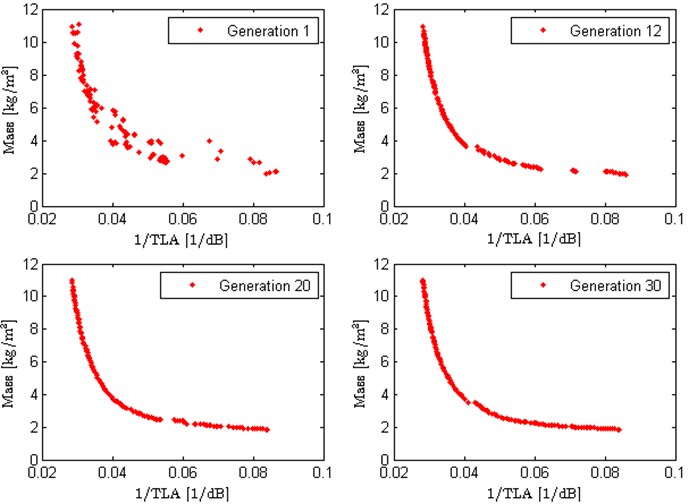
Considering the heavy computation caused by the complicated acoustic objective, the numerical experiments are performed in an appropriate problem size by setting the population size $N$ as 150 in all cases. Moreover, the sequential graphs in Fig. 2 illustrate the evolution of the objective function values at different generations, and the algorithm progresses from the random designs in generation 1 to a fairly well defined front of non-dominated designs in generation 30. In the figure, there appears to be only a slight improvement in the performance from generation 20 to generation 30. Therefore, the iteration is set as 30 generations in this paper.

Fig. 2Evolution of the objective function values with the increasing of generations

3.2. Results and discussions

3.2.1. Bi-objective Pareto front

This part demonstrates the Pareto optimal designs of the lightweight sandwich panel. For the numerical case in this subsection, the lower and upper bounds of face sheet thickness and core thickness are set as $L_{f} =$ 0.25 mm, $U_{f} =$ 2 mm, $L_{c} =$ 5 mm, $U_{c} =$ 50 mm, respectively.

Fig. 3 depicts the Pareto front of the lightweight sandwich panel. The horizontal and vertical axes represent the acoustic objective and mass objective, respectively. Note that the acoustic objective is the inverse of TLA, therefore the smaller the value on the horizontal axis, the better the sound insulation performance. From the figure it can be seen that a large number of Pareto optimal designs are generated and uniformly distributed with respect to the horizontal and vertical axes, which not only clearly illustrates the compromising solutions between two optimization objectives, but also verifies the effectiveness of the solution algorithm NSGA-II given in subsection 2.3. The two terminal points in the Pareto front represent the single-objective optimum solution for each axis separately. Point $A$ corresponds to the result of single acoustic objective optimization, which means the sandwich panel has the best sound insulation performance but the maximum total panel mass. Point $C$ corresponds to the result of single mass objective optimization and it means the sandwich panel has the minimum total panel mass but the worst sound insulation performance. According to [28], in the Pareto front, the middle part is the best interval to look for the optimum design points, and the break point usually contains interesting results comparing to other points. Therefore, point $B$ can be treated as the optimum design point, which implies the sound insulation performance and the total panel mass obtain the best compromising solutions.

Fig. 3Pareto front of the lightweight sandwich panel

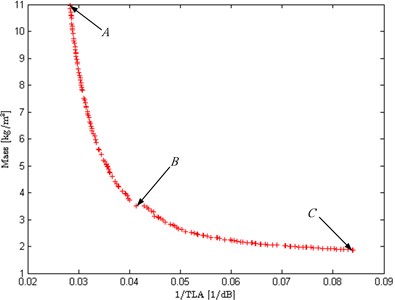
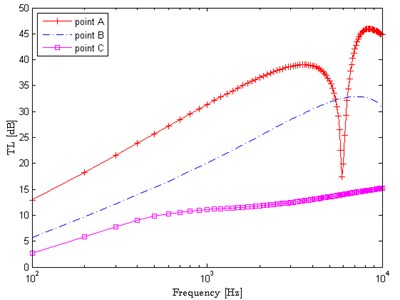
Fig. 4 shows the TL curves of the sandwich panel corresponding to the three typical points in Fig. 3. It can be seen from the figure that the lightweight sandwich panel has high coincident frequency, which means the sound insulation achieves better performance at low frequency. Compared with point $A$ , the TL curve in point $B$ becomes lower, however, the coincident frequency is enhanced, which indicates the frequency range of sound insulation is enlarged.

Fig. 4TL curves of the sandwich panel corresponding to the three typical points in the Pareto front

3.2.2. Effects of face sheet thickness bounds

The effects of face sheet thickness bounds on the optimization results of the sandwich panel are demonstrated in this part. For all numerical cases in this subsection, the bound of sandwich core thickness is set as [5, 50] mm.

In the two numerical cases, the upper bound of face sheet thickness $U_{f}$ is set as 2 mm, while the values of $L_{f}$ are different, i.e., $L_{f} =$ 0.25 mm and $L_{f} =$ 1 mm. Fig. 5 shows the effects of the face sheet thickness lower bound $L_{f}$ on the normalized optimal acoustic and mass objectives. In Fig. 5, the horizontal axis represents the optimized face sheet thickness $t_{f}$ and the vertical axis represents the normalized values of the acoustic objective TLA and the mass objective. From the figure we can see that the normalized TLA increases with $t_{f}$ nonlinearly, and the normalized panel mass increases with $t_{f}$ linearly. The lower bound of face sheet thickness $L_{f}$ has significantly effects on the optimization results. In addition, the larger the lower bound of face sheet thickness, the smaller the distance between the normalized TLA curve and mass curve, which means the two conflicting objectives could not achieve the best compromising solutions. In contrast, the smaller face sheet thickness lower bound could achieve the best trade-off between the TLA and the total panel mass. Therefore, in practical engineering design of lightweight sandwich panels, the smaller face sheet thickness lower bound can yield the better and more economical design scheme.

Fig. 5Effects of face sheet thickness lower bound on the optimization results

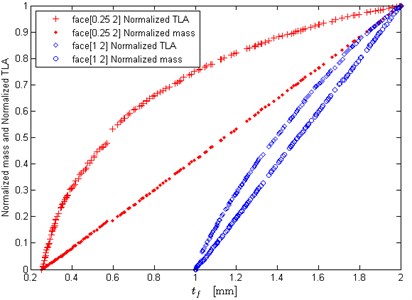
Fig. 6Effects of face sheet thickness upper bound on the optimization results

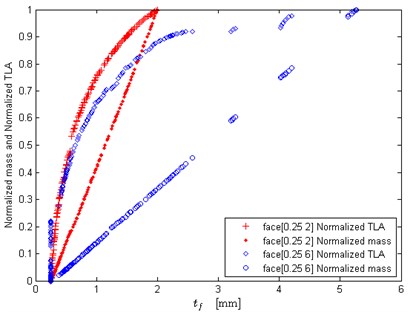
Furthermore, the lower bound of face sheet thickness $L_{f}$ is set as 0.25 mm, while the upper bound of face sheet thickness is set as 2 mm and 6 mm, respectively. Fig. 6 depicts the effects of face sheet thickness upper bound $U_{f}$ on the normalized optimization results. It can be seen that the upper bound of face sheet thickness $U_{f}$ has obvious influence on the optimization results. The larger $U_{f}$ can make the conflicting objectives better compromised, however, the jumping phenomenon appears in the curves. Due to the mechanical constraint, the two optimization objectives could not achieve compromising solutions in some parts of face sheet thickness. That is to say, in real-world engineering design, $U_{f}$ can adopt a relative larger value so as to obtain the better trade-off solutions, but it does not mean $U_{f}$ could be as large as possible.

3.2.3. Effects of core thickness bounds

In this part, the effects of sandwich core thickness bounds on the optimization results of the sandwich panel are demonstrated. For all numerical cases in this subsection, the bound of face sheet thickness is set as [0.25, 2] mm.

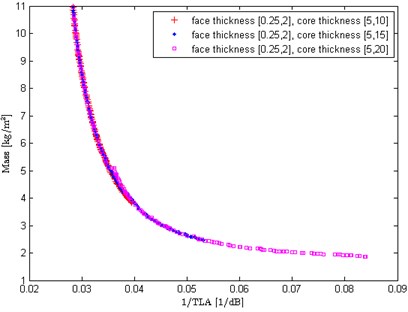
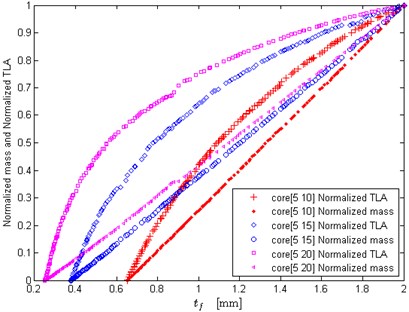
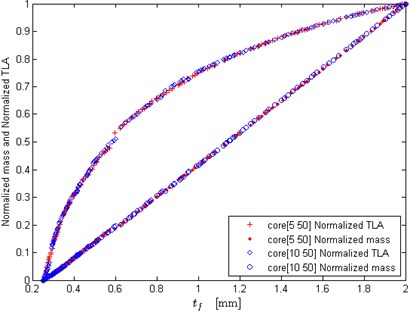
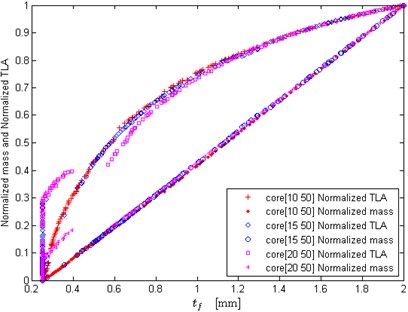
Fig. 7 and Fig. 8 show the effects of core thickness upper bound on the optimization results. The lower bound of core thickness $L_{c}$ is set as 5 mm, and the upper bound of core thickness $U_{c}$ is set as 10 mm, 15 mm, 20 mm, 30 mm and 50 mm, respectively. When the upper bound of core thickness $U_{c}$ is not too large, it has significant impact on the Pareto fronts (see Fig. 7(a)), and the normalized mass and TLA (see Fig. 7(b)). As we know, a perfect Pareto front usually has a distinct knee, and the solutions close to the knee can offer a good balance between the two objectives. It can be seen in Fig. 7(a), the Pareto front at the case of $U_{c} =$ 20 mm exhibits a distinct knee in the objective space, while the other two cases have not the knee. That is to say, if the $U_{c}$ equals to a smaller value, the two objectives might not achieve the compromising solutions, which implies the design scheme may be improper or not particularly economical. From Fig. 7(b) it also can be seen that when $U_{c}$ is set as a small value, such as $U_{c} =$ 10 mm, the optimized face sheet thickness $t_{f}$ could not choose the value from $L_{f}$ due to the mechanical constraint. That is to say, the small $U_{c}$ shortens the distance between the normalized TLA curve and mass curve, and could not make the acoustic performance design and the lightweight design of sandwich panel best compromised. Fig.8 shows that when the upper bound of core thickness $U_{c}$ becomes larger, it will yield little effect on the optimization results. Therefore, setting $U_{c}$ as a relatively large value can make the design scheme of sandwich panels more optimal.

Let the upper bound of core thickness $U_{c}$ be 50 mm, and the lower bound of core thickness $L_{c}$ is 5 mm, 10 mm, 15 mm and 20 mm, respectively. Fig. 9 shows the effects of core thickness lower bound $L_{c}$ on the normalized optimal mass and TLA. From Fig. 9(a) it can be observed that when the lower bound of core thickness $L_{c}$ is smaller, $L_{c}$ seems to have little impact on the optimization results. When $L_{c}$ becomes larger, such as $L_{c} =$ 15 mm or $L_{c} =$ 20 mm, $L_{c}$ poses a certain impact on the normalized mass and TLA in the range where $t_{f}$ equals to small values, as shown in Fig. 9(b). In general, the effects of core thickness lower bound on the optimization results are not much obvious. However, if $L_{c}$ approaches to small values as much as possible the design scheme could be more optimal.

Fig. 7Effects of core thickness upper bound on the optimization results (small upper bound)

a) Effects on Pareto fronts

b) Effects on normalized optimization results

Fig. 8Effects of core thickness upper bound on the optimization results (large upper bound)

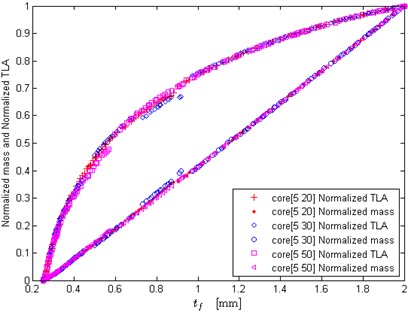
Fig. 9Effects of core thickness lower bound on the optimization results

a) Small lower bound

b) Large lower bound

4. Conclusions

A bi-objective optimal design problem of lightweight sandwich panels is investigated in this paper, which simultaneously maximizes the sound insulation performance and minimizes the total panel mass. To formulate the acoustic objective function, the acoustic model of the sandwich panel is discussed at first. Then a bi-objective optimization model subject to geometric and mechanical constraints is established, and the solution algorithm NSGA-II is finally proposed. To verify the effectiveness of the proposed optimization model and solution algorithm, and investigate the effects of geometric constraints on the optimization results, a number of numerical experiments are carried out. The obtained Pareto optimal designs are uniformly distributed and discussed from the viewpoint of engineering design. The numerical results show that the upper and lower bounds of face sheet thickness have significant impact on the optimization results of sandwich panels. When the upper bound of core thicknessis not too large, it also has obvious effects on the optimal solutions. The lower bound of core thickness poses a certain impact on the optimal solutions only in the range where the face sheet thicknessequals to small values. This study can provide a guidance for practitioners to optimize the design of acoustic performance for lightweight sandwich panels.

There are several areas that future work can focus on. A possible extension to this work is to further consider the objective of sandwich panel material cost and carry out the study on three-objective optimization. Another future work can focus on combining physical experiments with numerical simulation analysis together in the field of sandwich panel optimal design.

References

Cameron C. J., Wennhage P., Göransson P. Structural-acoustic design of a multi-functional sandwich panel in an automotive context. Journal of Sandwich Structures and Materials, Vol. 12, Issue 11, 2010, p. 684-708.

Publisher
Zhou J., Bhaskar A., Zhang X. Optimization for sound transmission through a double-wall panel. Applied Acoustics, Vol. 74, Issue 12, 2013, p. 1422-1428.

Publisher
Makris S. E., Smith J. M., Dym C. L. Multi-objective optimization of acoustic sandwich panels. Engineering Optimization, Vol. 13, Issue 2, 1988, p. 147-172.

Publisher
Makris S. E., Dym C. L., Smith J. M. Transmission loss optimization in acoustic sandwich panels. The Journal of the Acoustical Society of America, Vol. 79, Issue 6, 1986, p. 1833-1843.

Publisher
Lang M. A., Dym C. L. Optimal acoustic design of sandwich panels. The Journal of the Acoustical Society of America, Vol. 57, Issue 6, 1975, p. 1481-1487.

Publisher
Thamburaj P., Sun J. Q. Optimization of anisotropic sandwich beams for higher sound transmission loss. Journal of Sound and Vibration, Vol. 254, Issue 1, 2002, p. 23-36.

Publisher
Cameron C. J., Nordgren E. L., Wennhage P., Göransson P. On the balancing of structural and acoustic performance of a sandwich panel based on topology, property, and size optimization. Journal of Sound and Vibration, Vol. 333, Issue 13, 2014, p. 2677-2698.

Publisher
Leite P., Thomas M., Simon F., Bréchet Y. Optimal design of a multifunctional sandwich panel with foam core: lightweight design for flexural stiffness and acoustical transmission loss. Advanced Engineering Materials, Vol. 17, Issue 3, 2015, p. 311-318.

Publisher
Wennhage P. Weight minimization of sandwich panels with acoustic and mechanical constraints. Journal of Sandwich Structures and Materials, Vol. 3, Issue 1, 2001, p. 22-49.

Publisher
Wennhage P. Weight optimization of sandwich panel with acoustic constraints, experimental verification. Journal of Sandwich Structures and Materials, Vol. 4, Issue 4, 2002, p. 353-365.

Publisher
Wennhage P. Weight optimization of large scale sandwich structures with acoustic and mechanical constraints. Journal of Sandwich Structures and Materials, Vol. 5, Issue 3, 2003, p. 253-266.

Publisher
Wang T., Li S., Nutt S. R. Optimal design of acoustical sandwich panels with a genetic algorithm. Applied Acoustics, Vol. 70, Issue 3, 2009, p. 416-425.

Publisher
Guerich M., Assaf S. Optimization of noise transmission through sandwich structures. Journal of Vibration and Acoustics, Vol. 135, Issue 5, 2013, p. 051010.

Publisher
Hudson C. W., Carruthers J. J., Robinson A. M. Multiple objective optimisation of composite sandwich structures for rail vehicle floor panels. Composite Structures, Vol. 92, Issue 9, 2010, p. 2077-2082.

Publisher
Wang T., Sokolinsky V. S., Rajaram S., Nutt S. R. Assessment of sandwich models for the prediction of sound transmission loss in unidirectional sandwich panels. Applied Acoustics, Vol. 66, Issue 3, 2005, p. 245-262.

Publisher
Zhou R., Crocker M. J. Sound transmission characteristics of asymmetric sandwich panels. Journal of Vibration and Acoustics, Vol. 132, Issue 3, 2010, p. 031012.

Publisher
Fringuellino M., Guglielmone C. Progressive impedance method for the classical analysis of acoustic transmission loss in multilayered walls. Applied Acoustics, Vol. 59, Issue 3, 2000, p. 275-285.

Publisher
Pierce A. D. Acoustics: An Introduction to Its Physical Principles and Applications. McGraw-Hill Book Company, New York, 1981.

Search CrossRef
Beranek L. L., Ver I. L. Noise and Vibration Control Engineering: Principles and Applications. John Wiley and Sons, Inc., New York, 1992.

Search CrossRef
Dym C. L., Lang D. C. Transmission loss of damped asymmetric sandwich panels with orthotropic cores. Journal of Sound and Vibration, Vol. 88, Issue 3, 1983, p. 299-319.

Publisher
Allen H. G. Analysis and Design of Structural Sandwich Panels. Compton Printing Ltd., Aylesbury and London, 1969.

Publisher
Boyd S., Vandenberghe L. Convex Optimization. Cambridge University Press, 2004.

Publisher
Mistakidis E. S., Stavroulakis G. E. Nonconvex Optimization in Mechanics: Algorithms, Heuristics and Engineering Applications by the FEM. Springer, 2013.

Search CrossRef
Branke J. Evolutionary Optimization in Dynamic Environments, Springer, 2009.

Search CrossRef
Deb K., Pratap A., Agarwal S., Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, Vol. 6, Issue 2, 2002, p. 182-197.

Publisher
Sharma D., Deb K., Kishore N. N. Customized evolutionary optimization procedure for generating minimum weight compliant mechanisms. Engineering Optimization, Vol. 46, Issue 1, 2014, p. 39-60.

Publisher
Zhang D., Zheng L. Vibration characteristics analysis of CLD/plate based on the multi-objective optimization. Journal of Vibroengineering, Vol. 17, Issue 1, 2015, p. 309-329.

Search CrossRef
Khalkhali A., Narimanzadeh N., Khakshournia S., Amiri S. Optimal design of sandwich panels using multi-objective genetic algorithm and finite element method. International Journal of Engineering, Vol. 27, Issue 3, 2013, p. 395-402.

Publisher

Cited by

Free vibration analysis and multi-objective optimization of lattice sandwich beams

(2023)

Vibro-acoustic analysis of the sound transmission through aerospace composite structures

Hicham Kaidouchi | Said Kebdani | Sid Ahmed Slimane

(2023)

Modular sandwich panel system for non-loadbearing walls – Experimental mechanical, fire and acoustic testing

(2023)

Research on system identification based on hydraulic pump-motor of HMCVT

(2019)

Design and analysis of a portable greenhouse weeding machine

(2019)

Optimization of the Structural Parameters of Fisheye Contact Pairs by RSM

(2019)

Application of the Wave Propagation Approach to Sandwich Structures: Vibro-Acoustic Properties of Aluminum Honeycomb Materials

Edoardo Piana | Candida Petrogalli | Diego Paderno | Ulf Carlsson

(2018)

Driving Torque Model and Accuracy Test of Multilink High-Speed Punch

(2018)

Bearing fault feature extraction method based on complete ensemble empirical mode decomposition with adaptive noise

(2018)

About this article

Received

02 November 2015

Accepted

06 April 2016

Published

30 June 2016

SUBJECTS

Acoustics, noise control and engineering applications

DOI

https://doi.org/10.21595/jve.2016.16603

Keywords

sound insulation performance

sound transmission loss

lightweight sandwich panels

bi-objective optimization

genetic algorithm

Acknowledgements

Authors of the paper would like to express appreciation of the support from Jiangsu Postdoctoral Research Foundation (1402084C), Jiangsu Natural Science Foundation (BK20130977) and National Natural Science Foundation of China (11272159).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2017 12 31

A novel MPP-NSGA algorithm and its application in optimization for radiated noises in the aircraft cabin

Jie Li, Wei Xing Liu, Yu Zhu Zhang, Ling Zhang, Shan Shan Li

Research article

2017 06 30

Numerical optimization of sound pressure responses for the dash panel based on automatically matched layer and genetic algorithm

Xin Zhe Zhang, Guo Jie Zhang

Research article

2017 05 30

Optimization for heat and sound insulation of honeycomb sandwich panel in thermal environments

Jinlong Yuan, Haibo Chen, Qiang Zhong, Kongjuan Li

Research article

2016 02 15

Numerical optimization of sound insulation performance for the new type glass window based on genetic algorithm and its application in high-speed trains

Li Yang

X.- Xu, Y.- Jiang, H.- Lee, and N. Chen, “Sound insulation performance optimization of lightweight sandwich panels,” Journal of Vibroengineering, Vol. 18, No. 4, pp. 2574–2586, Jun. 2016, https://doi.org/10.21595/jve.2016.16603

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.16603
UR  - https://doi.org/10.21595/jve.2016.16603
TI  - Sound insulation performance optimization of lightweight sandwich panels
T2  - Journal of Vibroengineering
AU  - Xu, Xiao-mei
AU  - Jiang, Yi-ping
AU  - Lee, Heow-pueh
AU  - Chen, Ning
PY  - 2016
DA  - 2016/06/30
PB  - JVE International Ltd.
SP  - 2574-2586
IS  - 4
VL  - 18
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Xu_2016,
	doi = {10.21595/jve.2016.16603},
	url = {https://doi.org/10.21595/jve.2016.16603},
	year = 2016,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {18},
	number = {4},
	pages = {2574--2586},
	author = {Xiao-mei Xu and Yi-ping Jiang and Heow-pueh Lee and Ning Chen},
	title = {Sound insulation performance optimization of lightweight sandwich panels},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]X. Xu, Y. Jiang, H. Lee, and N. Chen, “Sound insulation performance optimization of lightweight sandwich panels,” Journal of Vibroengineering, vol. 18, no. 4, pp. 2574–2586, Jun. 2016, doi: 10.21595/jve.2016.16603.

Copy IEEE

Copied to clipboard!

Xu, Xiao-mei, Yi-ping Jiang, Heow-pueh Lee, and Ning Chen. “Sound Insulation Performance Optimization of Lightweight Sandwich Panels.” Journal of Vibroengineering 18, no. 4 (June 30, 2016): 2574–86. https://doi.org/10.21595/jve.2016.16603.

Copy Chicago

Copied to clipboard!

Sound insulation performance optimization of lightweight sandwich panels

Abstract

1. Introduction

2. Theoretical formulation

2.1. Acoustic model of sandwich panels

2.2. Optimization model formulation

2.2.1. Objective function

2.2.1.1. Acoustic objective

2.2.1.2. Mass objective

2.2.2. Constraints

2.2.3. Complexity analysis

2.3. Solution algorithm

3. Numerical experiments

3.1. Experimental settings

3.2. Results and discussions

3.2.1. Bi-objective Pareto front

3.2.2. Effects of face sheet thickness bounds

3.2.3. Effects of core thickness bounds

4. Conclusions

References

Cited by

About this article

Related Articles