Power quality prediction based on least squares method

3.1. Power quality and time

First, from the power quality (bias pass rate) and the relationship between time to start. This assumes that the annual electricity consumption is cyclical (such as the annual peak is the annual electricity consumption), due to power quality affected by the electricity situation, it is also a cyclical change. The following is an analysis of the results of the study.

First, from the power quality (bias pass rate) and the relationship between time to start. This assumes that the annual electricity consumption is cyclical (such as the annual peak is the annual electricity consumption), due to power quality affected by the electricity situation, it is also a cyclical change.

Fig. 1The trend of voltage qualification rate with time and voltage grade and voltage qualified rate

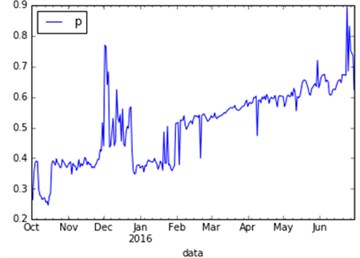
a)

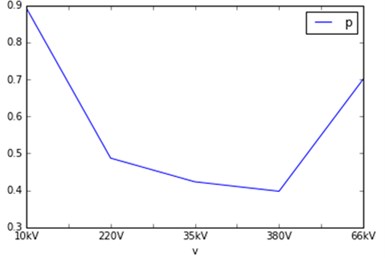
b)

Build the line graph of the voltage passing rate of power grid with time, as shown in Fig. 1(a). Through the analysis, the change trend of qualified rate can be divided into two stages, that is, from October 2015 to February 2016 and February to June 2016, the overall trend of voltage qualification rate in the previous stage fluctuates from 0.4 to December out is a sudden surge in the peak to 0.8 and then back to 0.4. The latter stage of the overall upward trend, the voltage qualified rate climbed from 0.5 to 0.8. If the assumption is that the law can be used as a reference condition, the time for the analysis of electricity influence factors of quality.

3.2. Voltage qualification and voltage rating

Analysis of the relationship between voltage qualification and voltage level is to confirm the different voltage level of the voltage qualified rate of the existence of significant differences with the analysis of the same time if the voltage rating if the different voltage there are significant differences in the qualified power quality prediction can be assisted. As shown in Fig. 1(b) it can be observed that the pass rate does not change monotonically with the rise of the voltage level, but the difference of the average of the pass rates of different voltage levels has obvious influence on the prediction. 10 kV voltage level of which the highest average of the pass rate in the vicinity of 0.9, 380 V minimum average of 0.4, 220 V and 66 kV of the pass rate average of 0.5, 0.7 around.

3.3. Voltage qualification and voltage average

The average voltage is the most basic data of the grid, if you can predict the voltage quality will greatly improve the efficiency of the forecast.

First of all, the data according to the least squares method to do binomial fitting, as shown in Fig. 2(a) (abscissa for the voltage average, the vertical axis voltage for the pass rate, the black point for the real data points, the blue line for binomial fitting). It can be seen from the image that although the fitting curve has a certain trend, it is not fitted with the real data points, and the distribution of the data points does not accord with any function class. This is due to the fact that the magnitude of the data is not uniform. Therefore, the data are classified according to the magnitude of magnitude, and normalized data, the average value of the size of the –1 to 1 interval, fitted as shown in Fig. 2(b). It can be found that although the data points are more concentrated at this time, the distribution is still not suitable for fitting.

Fig. 2Voltage qualification rate varies with voltage average

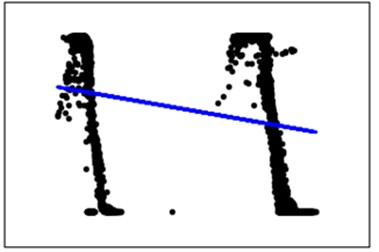
a) Overall

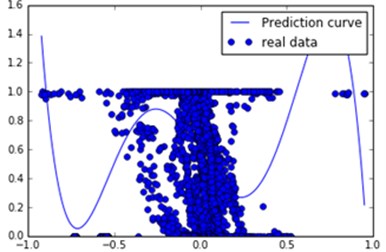
b) Normalized

Since the results of the previous two-step analysis does not satisfy the requirements, the data are further divided into each monitoring point to obtain a large number of fitting images and fitting functions. It is found that some of the results are shown in Fig. 3. The qualification is concentrated around a constant value 1 in Fig. 3. Some results are shown in Fig. 4(a). Pass rate with the average voltage increases gradually decreased, the curve for the pentagonal fitting results. Part of the results shown in Fig. 4(b) the pass rate with the average voltage curve into a parabolic type, through the seven-type and the fitting curves of the obtained curve and the data distribution are high.

The results show that there is a relationship between voltage level and voltage average, but the relational model is not unique. Summary The relationship between qualification and average voltage can be categorized as the above-mentioned three types of line distribution: parallel line distribution (binomial fitting – Fig. 3), curve descent distribution (pentad fitting – Fig. 4(a)). Parabola-like distribution (seven-term fit – Fig. 4(b)). The latter two kinds of distribution are the majority, and the parabola distribution is more easily explained according to the meaning of the pass rate. When the bias voltage qualification rate is high, the voltage is distributed in the rated voltage (Fig. 4(b) parabola top). When the bias voltage qualification rate is low, the voltage is distributed outside the rated voltage (Fig. 4(b) parabola on both sides). According to the analysis, the voltage level can be used as an auxiliary indicator to predict the power quality. This contributes to the power quality analysis work.

Fig. 3The voltage qualification rate changes with the voltage average (monitoring point 1)

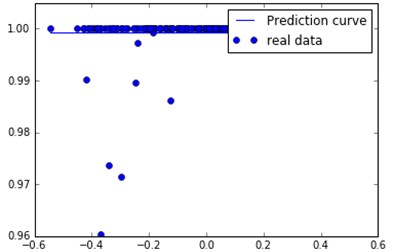
Fig. 4The voltage qualification rate varies with the average voltage

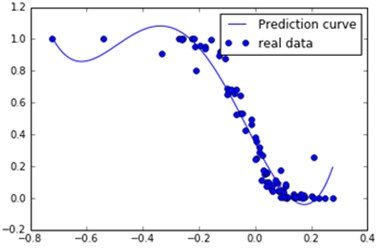
a) Monitoring point 2

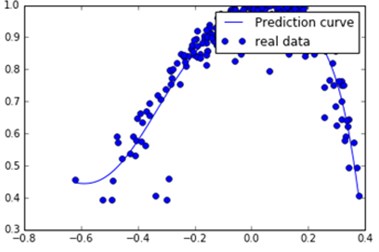
b) Monitoring point 3

3.4. Voltage qualification and voltage rating

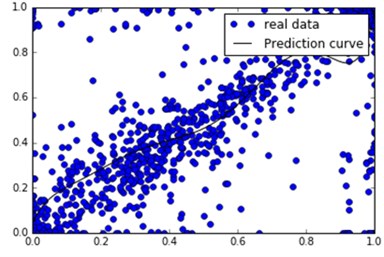
Finally, the relationship between the ‘$\text{'}$’ the bias voltage qualification rate and the bias voltage qualification rate ‘$\text{'}$’ – the input point ($x$, $y$), $y$ for the day a pass rate, $x$ is y the day before the pass rate (For the convenience of description is called the bias voltage qualification of transfer). The overall data is analyzed by this rule, and the results are shown in Fig. 5(a). It can be seen that the pass rate of the whole data is positive correlation, and the binomial fitting coefficient is [0.88184171 0.04795697]. The following step-by-step analysis.

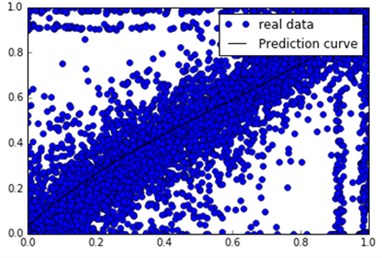
In the process of average voltage analysis, the pass rate of the monitoring points is analyzed. It should be noted here and not one by one analysis of monitoring points, but to five monitoring points as a unit, the first fitting into a unit, then every increase in a unit of observed changes in fitting. Fig. 5, Fig. 6 (from l top to bottom as a unit, 2 units, 10 units), when the input of a unit when the curve of the larger fluctuations in fitting. When lost the fitting curves of two units are relatively flat, and the diagonal data sets are more obvious. When entering ten the unit has no significant fluctuations in the polyline.

To sum up the analysis shows that the bias voltage qualification is a positive correlation, which is also consistent with common sense. When a regional power appear, problems will continue to have an impact on follow-up work. This indicates that the power quality can be predicted based on the bias voltage qualification rate, and use it to build the model

Fig. 5The relationship between the voltage bias and the voltage bias

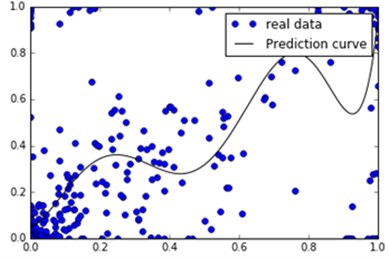
a)

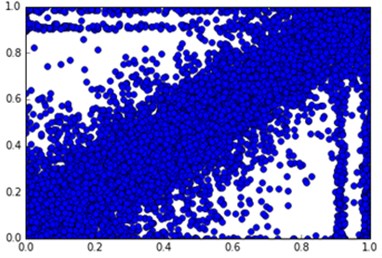
b)

Fig. 6The relationship between the voltage bias and the voltage bias

a) Two units

b) Ten units