Behavioral models of nonlinear filters based on discrete time cellular neural networks

1. Introduction

The behavioral models of nonlinear dynamic systems are constructed with using the sets of input and output signals as well as taking into account the information (knowledge) about these systems. Depending on the volume of a priori assigned knowledge, three levels are distinguished, namely, “white, grey and black box” [1, 2]. The less volume of the information about a dynamic system is known, the darker an investigated object is getting. The “black box” level is established in the absence of any information about a system.

Let’s highlight the “black box” approach. The reasons of turning to the “black box” methodology are the following [3]:

– the functional complexity of dynamic systems,

– the high level of the system integration,

– lack of the knowledge of the system parameters and characteristics,

– new high requirements to the parameters and characteristics of precision technique.

Some technical tasks can be formulated as problems, which are solved within the framework of the input/output relationship. Basing on the dynamic system description, the identification, modeling and synthesis can be characterized as follows.

The identification is the process of constructing a nonlinear operator (the determination of the model parameters by solving the optimization task) using the known set of input and output signals. The test input signals can be both deterministic and random ones.

The mathematical modeling is the using of the mathematical model, obtained in the identification process, for calculating nonlinear system output signals.

The synthesis is the creation of hardware or software implemented device with desirable goal, for example, for compensation, filtration, detection and so on [4, 5].

The stages of the “black box” modeling are the following:

– forming the sets of input and output signals of a modeled object,

– selecting the model type and its complexity,

– defining the model parameters on solving the approximation task with assigned error,

– validating a designed model.

The relationship between the input and output signal sets is described by the equation:

The operator $F$ in Eq. (1) approximates the output $y$ on the basis of the previous output observation $y_{past}$ and the input $u$.

According to the “black box” approach, the unique input/output relationship is established. The property of uniqueness means that there is no situation when any input signal from the corresponding set is mapped into two or more output signals [1-3].

2. Turning to neural models

The development of systems with very large-scale integration and widely practiced computer art caused immense interest in neural networks and substantial progress in their investigation in recent years.

On synthesizing neural networks, the complicated matter of the knowledge representation in the network is being solved. A priori information and invariants must be taken into account in order to simplify the architecture and learning process of the network. This problem plays the special part since the proper network configuration facilitates its specialization that is very important in view of the following reasons [6, 7]:

– the neural network having specialized structure usually comprises less number of free parameters, which are to be adjusted than fully connected network does. Consequently, less amount of data is required for specialized network learning. Moreover, it takes less time, and such a network possesses much better generalization power;

– specialized networks are characterized by more network capacity;

– the implementation cost of specialized neural networks decreases because their size is significantly less than that of fully connected networks.

Nowadays, there is no clear solution of the problem how to construct specialized neural networks taking into account a priori information. Nevertheless, there are many forms of neural networks already developed, among which an acceptable structure (or structures) can be selected after estimation of their advantages and drawbacks and used for solving various research problems connected with maths, physics, engineering, neurobiology, psychology. In the course of developing the neural network theory, the sciences mentioned above will raise their theoretical and applied potentialities as well [6, 7].

3. Example of nonlinear filters modeling to cancel non-Gaussian noise

The problem of non-Gaussian noise filter synthesis is often effectively solved within the framework of the “black box” approach. According to this approach, the mathematical filter model describes the relationship between the sets of input and output signals. The model parameters are determined by solving the approximation problem in the mean-square norm.

Nonlinear filters are synthesized on the class of bit-map (dot element) half-tone images at the resolution measured by 256 gray levels, i.e., image is the matrix of integers (elements of brightness, pixels) in the interval [0; 255]. The pixel format is unit8. The impulse noise model is assigned as “salt and pepper” [8].

Four types of nonlinear filter are applied to cancel the impulse noise in distorted images. Every filter is the cascade connection of the median filter with the 3x3 square aperture and a nonlinear unit in the form of either a neural network or polynomial.

The first type of the filter is suggested to build as the cascade connection of the median filter [8] and the discrete-time feedforward cellular neural network with the unity gain piecewise linear saturation function. Hereinafter, this filter is referred to as the combined discrete-time cellular neural network (CDTCNN).

The dynamics of a cell $C_{ij}$ in the feedforward cellular neural network is obtained by the following differential equation [9]:

where $x_{ij}\left(t\right)$ denotes the state of the cell $C_{ij}$, $u_{kl}\left(t\right)$ denotes the input of cell $C_{kl}$ located in the sphere of influence with radius $r$, $t$ is the continuous time, $b_{kl}$ is the feedforward synapse weight, $z$ is the bias term.

The cell denoted as $C_{ij}$ is located in the position $(i,\mathrm{}j)$ of the two-dimensional $M\times N$ area, and its $r$-neighborhood $N_{ij}^r$ is defined as follows:

where the size of the neighborhood $r$ is a positive integer number.

The element $u_{kl}\left(t\right)$ in Eq. (2) is obtained by moving a mask with the 3×3 window to the position $(i,\mathrm{}j)$ of the $M\times N$ input image.

In the discrete time domain, Eq. (2) is turned into the equation:

where $n$ is the normalized discrete time.

The output signal $y_{ij}\left(n\right)$ of the cell $C_{ij}$ results from treating by the nonlinear activation function $f(\cdot )$, which is usually specified as the unity gain piecewise linear saturation function described by the expression:

Eventually, the CDTCNN cell model is formed on the basis of Eqs. (4-5) in the two-dimensional $M\times N$ area described by Eq. (3).

The second type of the nonlinear filter synthesized is the cascade connection of the median filter [8] and the two-layer perceptron network with the hyperbolic tangent activation functions [6-8], referred to as the combined two-layer perceptron network (CTLPN). The third type is the cascade connection of the median filter and the Volterra filter [1-3], referred to as the combined Volterra filter (CVF). The fourth type is the median filter (MF) performed at the 3×3 square aperture [8].

The parameters of the CDTCNN with five cells, the CTLPN including five neurons in the hidden layer and the CVF of the second degree are defined on solving the approximation problem in the mean-square norm while using learning image with the size of 220×148 pixels. The length of the learning sequence $u\left(n\right)$ in Eq. (4-5) amounts to 32560 samples.

On filtering images, mean-square errors are estimated according to the formula:

where $y\left(n\right)$ is the output signal of nonlinear filter, $y^o\left(n\right)$ is a desirable signal, $Q=\text{32 560}$.

Mean-square errors defined by Eq. (6) are summarized in Table 1 under the impulse noise density equaled 0.5. “Tigers”, “Building” and “Fence” are the names of learning and two test images, correspondently. All the images have the size of 220×148 pixels.

The results of nonlinear filtering is distinctly represented in Fig. 1. Fig. 1(a) illustrates the initial test image “Fence”, Fig. 1(b) – the image destoted by the impulse noise with the probebility density equaled 0.5, Fig. 1(c) – the CDTCNN result, Fig. 1(d) – the CTLPN result, Fig. 1(e) – the CVF result, Fig. 1(f) – the MF result.

One can see from Table 1 and Fig. 1, the offed CDTCNN yields higher filtration precision, than the CTLPN, the CVF and the MF. It should be observed that the CDTCNN, the CTLPN and the CVF provide different accuracy at the nearly equal complexity of these filters (56 parameters of the CDTCNN and the CTLPN, 54 parameters of the CVF).

The use of the hyperbolic tangent activation functions in the CTLPN negatively affects the image quality (white color turns to gray one, as well as there is a bit ripple i.e. image loses its smoothness (Fig. 1(d)). Indeed, at an equal probability of the impulse noise (for instance, white and black dots on images) occurrence, the filtration with different gains at low and high amplitudes of signals (in case of the hyperbolic tangent) is not expedient.

In practice, the CDTCNN is more preferable in comparison with the CTLPN since its hardware implementation is simple due to using the piecewise linear saturation functions.

Fig. 1Output signals of nonlinear filters

a)

b)

c)

d)

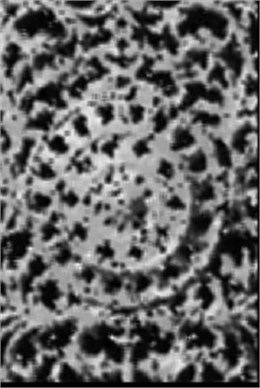
e)

f)

4. Conclusions

The mathematical modeling of nonlinear dynamic systems are frequently carried out based on the input/output system relationship by means of neural networks.

The combined discrete time feedforward cellular neural network is proposed for the impulse noise filtration on half-tone images. This neural network with the piecewise linear saturation functions carries out more accurate restoration of images in comparison with the combined two-layer perceptron network comprising the hyperbolic tangent activation functions, the combined Volterra filter and the median filter.

It should be emphasized that the hardware implementation of the cellular neural network is simpler in comparison with the two-layer perceptron network since the piecewise linear saturation functions used in the cellular network are simpler than the hyperbolic tangent activation functions included in the perceptron network.