Optimization of thread affinity and memory affinity for remote core locking synchronization in multithreaded programs for multicore computer systems

1. Introduction

Currently distributed computer systems (CS) [1] are large-scale and include multiple architectures. These systems are composed of shared memory multi-core compute nodes (SMP, NUMA systems) equipped by universal processors as well as specialized accelerators. System software must consider the large scale, multiple architectures and hierarchical structure. Parallel programs for multi-core CS are multithreaded in most cases. The software must ensure linear speedup with a large amount of threads. Thread synchronization while accessing to shared data structures is one of the most significant problem in multithreading programming. The existing approaches for thread synchronization include locks, lock-free algorithms and concurrent data structures [2] and software transactional memory [3].

The main drawbacks of lock-free algorithms and data structures are the limited application scope and high complexity of development of programs [2, 4, 5]. Furthermore, the development of lock-free algorithms and data structures includes the problems, connected with ABA problem [6, 7], poor performance and restricted nature of atomic operations. Software transactional memory nowadays have a variety of issues and does not ensure sufficient performance of multithreaded programs and is not applied in common real applications for now.

Conventional approach for synchronization by lock-based critical sections is still the most widespread. Locks are simple in usage and ensure the acceptable performance. Furthermore, the most of existing multithreaded programs utilizes lock-based approach. Thereby scalable algorithms and software tools for lock-based synchronization is very important today. Lock scalability depends on resolutions of the problems, connected with access contention of threads and locality of references. Access contention arises when multiple threads access to a critical section, protected by one lock. In the terms of hardware, it leads to the huge load to the data bus and cache memory inefficiency.

The main approaches for scalable lock implementations are CAS spinlocks [8], MCS-locks [9], Flat combining [10], CC-Synch [11], DSM-Synch [11], Oyama lock [12]. Some of the existing works also includes the methods for localization access to cache memory [10, 13-15]. The works [14, 15] are devoted to concurrent data structures development (lists and hash tables) based on critical section execution on dedicated processor cores. The paper [13] propose universal hardware solution, which includes the set of processor instructions for transferring the ownership to a dedicated processor core. Flat Combining [10] refers to software approaches and suggests the server threads (all the threads become server threads by order), which execute critical sections.

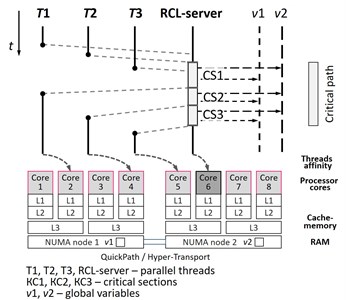
This paper considers Remote Core Locking (RCL) method [16, 17]. RCL minimizes execution time of existing programs thanks to critical path reduction. This technique assumes replacement of high-load critical sections in existing multithreading applications to remote functions calls for its execution on dedicated processor cores (Fig. 1).

The current implementation of RCL has several drawbacks. There is no memory affinity for NUMA systems. The latency of RCL-server addresses to the shared memory areas is essential for the execution time of a program. Memory allocation on the NUMA-node, which is not local to the node, on which RCL-server is running, leads to severe overheads when RCL-server addresses to the variables allocated on remote nodes. RCL also has no mechanism of automatic selection of processor cores for server thread and working threads with considering the structure of computer system and existing affinity. The processor affinity greatly effects on the overheads caused by localization of access to the global variables. Therefore, user threads should be executed on the processors cores, located as more “close” to the processor core of RCL-server. In the existing RCL implementation user have to choose processor core for RCL-server and working threads by hands. Thus, the tools for automation of this procedure is the actual problem.

This work proposes the algorithm of RCL-locks initialization, which realizes memory affinity to the NUMA-nodes and RCL-server affinity to the processor cores, and the algorithm of sub-optimal affinity of working threads to the processor cores. The algorithms consider the hierarchical structure of multi-core CS and non-uniform memory access in NUMA-systems to minimize critical sections execution time.

Fig. 1Remote core locking (RCL)

2. RCL optimization algorithms

Let there is multi-core CS with shared memory, including $N$ processor cores: $P=\left\{1,2,\dots ,N\right\}$. Computer system has hierarchical structure, which can be described as a tree, comprising $L$ levels Fig. 2. Each level of the system is represented by individual type of structural elements of CS (NUMA-nodes, processor cores and multilevel cache-memory). We introduce the notation: $c_{lk}$ – the number of processor cores, owned by childs of an element $k\in \left\{1,2,\dots ,n_l\right\}$ from the level $l\in \left\{1,2,\dots ,L\right\}$; $r=p\left(l,k\right)$ – the first direct parent element $r\in \left\{1,2,\dots ,n_{l-1}\right\}$ for an element $k$, located on the level $l$; $m$ – the number of NUMA-nodes of multi-core CS; $j=m\left(i\right)$ – number $j\in \left\{1,2,\dots ,m\right\}$ of NUMA-node, containing a processor core $i$; $q_i$ – the set of processor cores, belonging to the NUMA-node $i$.

For the memory affinity optimization and RCL-server processor affinity optimization we propose the algorithm RCLLockInitNUMA of initialization of RCL-lock Fig. 3(a). The algorithm considers the non-uniform memory access and is performed during the initialization of RCL-lock.

On the first stage (lines 2-10) we compute the number of cores which is not busy by the RCL-server and used on each of NUMA-node. Further (lines 12-18) we compute the summary number of NUMA-nodes with the RCL-servers. If there is only one such node, we set the memory affinity to this node (lines 19-21). The second stage of the algorithm (lines 23-34) includes the search of sub-optimal processor core and the affinity of RCL-server to it. If there is only one not busy by RCL-server processor core in the system, set the affinity of the RCL-server to the next already occupied processor core (lines 23-24). One core is always free to run working threads on it. If there are more than one free processor core in the system, we search the least busy NUMA-node (line 26) and set the affinity of RCL-server to the first free core in this node (lines 27-32). The algorithms are finished by call of function of RCL-lock initialization with selected affinity.

Fig. 2An example of hierarchical structure of multi-core CS N= 8, L= 5, m= 2, c23= 2, p3;4= 2, m= 2, m3= 1

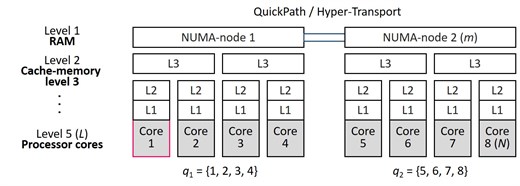
Fig. 3Algorithms RCLLockInitNUMA and RCLHierarchicalAffinity

For the optimization of thread affinity, we propose the algorithm RCLHierarchicalAffinity Fig. 3(b). The algorithm takes into account the structure of CS to minimize the execution time of programs with RCL. That algorithm is executed each time when parallel thread is created.

On the first stage (line 1) we check if the thread is not RCL-server. For each of thread we search all the RCL-servers (lines 3-4) executed in the system. After that when first processor core with RCL-server is found, this core becomes the current element (lines 6-7) and we search the nearest free processor core for the affinity of created thread (lines 4-35). In the beginning of the algorithm processor core with no attached threads is the free core (line 5). On the first stage of the core search we find first covering element of hierarchical structure. Covering element includes current element and contains more number of processor cores than it (lines 12-16). When the uppermost element of hierarchical structure is reached we increment the minimal number of threads per core (the free core now is the core with more number of attached threads) (lines 19-21). When the covering element is found we search first free core in it (lines 24-29) and set the affinity of created thread to it (line 32). Wherein for this core the number of threads executed on it is increased (line 33). After the affinity of the thread is set the algorithm is finished (line 34).

3. Experimental results

The experiments were conducted on the nodes of computer clusters Oak and Jet of Center of parallel computational technologies of Siberian state university of telecommunications and information sciences. The node of Oak includes two quad-core processors Intel Xeon E5620. The ratio of rate of access to local and remote NUMA-nodes are 21 to 10. The node of cluster Jet is equipped by quad-core processor Intel Xeon E5420. On the computing nodes, the operating systems CentOS 6 (Oak) and Fedora 21 (Jet) are installed. The compiler GCC 5.3.0 was used.

The benchmark performs iterative access to the elements of integer array of length $b=$ 5×10⁸ elements inside the critical sections, organized with RCL. The number of operations $n=$ 10⁸/$p$. As the operation in the critical section we used the increment of a variable by 1. As the access patterns three patterns were used: sequential access (on each new iteration choose the element, following the previous one), strided access (choose the element with the index more by $s=$ 20 than the previous one), random access (randomly choose the element). Number $p$ of parallel threads was varied from 2 to 7 (7 – number of not busy by RCL-server cores on the computing node) in the first experiment and from 2 to 100 in the second one. The throughput $b=n/t$ of the structure was used as an indicator of efficiency (here $t$ is time of benchmark execution).

We compared the efficiency of the algorithms RCLLockInitDefault (current RCL-lock initialization function) and RCLLockInitNUMA. Also, we compared the affinity of the threads obtained by the algorithms RCLHierarchicalAffinity with other random arbitrary affinities.

The Fig. 4 depicts the throughput $b$ of critical section with number $p$ of working threads. We can see that the algorithm RCLLockInitNUMA minimizes by 10-20 % the throughput of critical section at random access to the elements of test array and at strided access. In these access patterns data is not cached in the local cache of processor core, on which RCL-server is running. Therefore RCL-server address to the RAM directly, wherein the access rate depends on data location in local or remote NUMA-node. The effect is perceptible at the number of threads comparable to the number of processor cores Fig. 4(a), as like for greater number of threads Fig. 4(b) and significantly do not change when the number of threads is changing. The fixed affinity of threads to processor cores insignificantly affect to the throughput.

The Fig. 5 represent the experimental results of different affinities for the benchmark. The algorithm RCLHierarchicalAffinity significantly increases critical section throughput. The effect of the algorithms depends on number of threads (up to 2.4 times at $p=$ 2, up to 2.2 times at $p=$ 3, up to 1.3 times at $p=$ 4, up to 1.2 times at $p=$ 5 and an access pattern (up to 1.5 times at random access, up to 2.4 times at sequential access and up to 2.1 times at strided access).

Fig. 4Efficiency of the algorithms of RCL-lock initalization, cluster Oak. a–p= 2,…, 7, b–p= 2,…, 100. 1 – RCLLockInitNUMA, sequential access, 2 – RCLLockInitDefault, sequential access, 3 – RCLLockInitNUMA, strided access, 4 – RCLLockInitDefault, strided access, 5 – RCLLockInitNUMA, random access, 6 – RCLLockInitDefault, random access

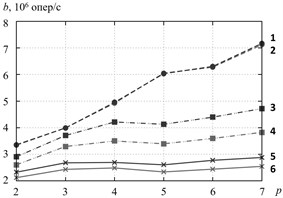
a)

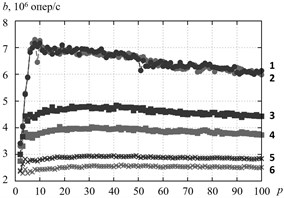
b)

Fig. 5Threads affinity efficiency comparison, cluster Oak. a–p= 2, b–p= 3, c–p= 4, d–p= 5. – RCLLockInitDefault, random access, – RCLLockInitDefault, sequential access, – RCLLockInitDefault, strided access, – RCLLockInitNUMA, random access, – RCLLockInitNUMA, sequential access, – RCLLockInitNUMA, strided access, – working thread, – RCL-server, – thread allocating the memory

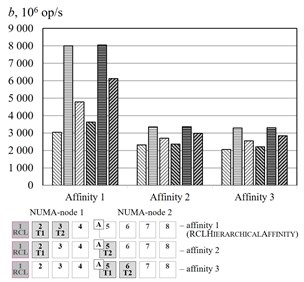
a)

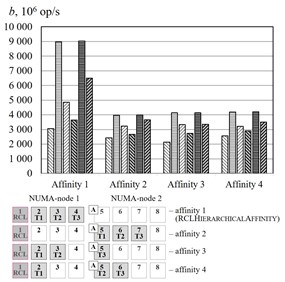
b)

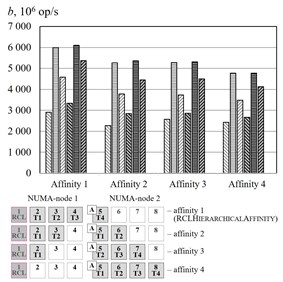
c)

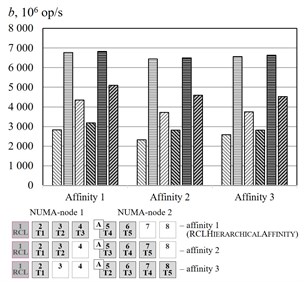
d)

4. Conclusions

We proposed the algorithm RCLLockInitNUMA of initialization of RCL-lock with considering the non-uniform memory access in multi-core NUMA-systems and the algorithm RCLHierarchicalAffinity of sub-optimal thread affinity in hierarchical multi-core computer systems. The algorithm RCLLockInitNUMA increases by 10-20 % at the average the throughput of critical sections of parallel multithreaded programs based on RCL at random access and strided access to the elements of arrays on the NUMA multi-core systems. The optimization is reached by means of minimization of number of addresses to remote memory NUMA-segments. The algorithm RCLHierarchicalAffinity increases the throughput of critical section up to 1.2-2.4 times for all access templates on some computer systems. The algorithms realize the affinity with considering all the hierarchical levels of multi-core computer systems. The developed algorithms are realized as a library and may be used to minimize existing programs based of RCL.