Lifting load monitoring of mine hoist through vibration signal analysis with variational mode decomposition

1. Introduction

In vertical-shaft transportation, mine hoist is a very important item of equipment, which is used to transport personnel, materials, equipment, and coal between the underground and surface areas. Under operation involving frequent start-stopping, high speed, and heavy loads, the accidental occurrence of a malignant fault, such as skidding, overloading, or pot-sticking, may cause a fatal crash and affect the safety of the mine and its production efficiency. The common faults of mine hoist are related to its lifting load. However, the mine hoist system is employed in a semi-closed deep and narrow space, and the ropes and hoisting conveyance are large-span moving parts. Therefore, it is difficult to directly measure the mine-hoist lifting load. Vibration signals can effectively provide health information on a large rotary machine, and many studies on vibration usage have been performed by researchers throughout the world [1-4]. That is, vibration signal analysis constitutes a new method of monitoring the lifting load of mine hoist.

Vibration signal is a kind of high-frequency transient signal, and it is difficult to directly use such a signal to accurately identify the lifting load conditions of mine hoist. Thus, signal processing methods should be used to extract the condition-related features for lifting load identification. To date, many techniques have been introduced for the analysis of vibration signals in the time, frequency, and time-frequency domains [5]. Time-domain analysis is the simplest method for feature extraction, and statistical indicators are usually obtained to monitor the mechanical health [6-8]. For frequency-domain analysis, the time-domain signals are mainly transformed into frequency-domain signals through Fourier-transform (FT)-based signal processing methods [9-13], and the frequency related information is then used for health monitoring. Regardless of whether time- or frequency-domain analysis is employed, however, only partial information can be obtained. To achieve more detailed analysis, time-frequency analysis methods have been introduced for signal processing, such as the short-time FT (STFT) [14, 15], Wigner-Ville distribution (WVD) [16], wavelet transform (WT)-based methods [17-19], empirical mode decomposition (EMD) [20], ensemble EMD (EEMD) [21], and variational mode decomposition (VMD) [22].

Among these methods, VMD can adaptively find the frequency center and bandwidth of each component by iteratively searching for the optimal solutions of variational models. This approach has frequently been used to analyze complicated signals in recent years. For example, in [23], an underdetermined blind source separation is proposed, in which VMD is employed to analyze the compound roller-bearing fault signals and the fault-relative features are accurately extracted. Yao et al. [24] have employed VMD and robust independent component analysis to achieve noise source identification for a diesel engine; their results show that the proposed method can accurately separate and identify the combustion noise and piston slap noise. A fault diagnosis method for multistage centrifugal pump based on VMD is designed in [25], and a comparison of the VMD and EMD fault feature extraction performance shows that the former can accurately extract the principal mode of the bearing faults more effectively. Liu et al. [26] have proposed a novel signal denoising method that combines VMD and detrended fluctuation analysis (DFA), labeled “DFA-VMD”; the order of time complexity of this method is equivalent to that of EMD. In [27], a novel fault diagnosis method for wind turbine based on VMD and Teager energy operator is proposed. The above methods indicate that VMD is an effective signal processing method for complicated signals.

Through application of a signal processing method, features can be extracted. However, development of a method for employing these techniques for lifting load condition identification is also important. In this work, a novel lifting load monitoring method for a mine hoist, which is based on VMD and a support vector machine (SVM) through vibration signal analysis, is proposed. The remainder of this paper is structured as follows. Section 2 introduces the theoretical basis, which includes overviews of EMD and VMD. The recognition model of the mine-hoist lifting load is described in Section 3. Section 4 presents a verification of the proposed signal processing method, which is achieved through simulation analysis. Finally, the experimental study is presented and discussed in Section 5, and the conclusion is given in Section 6.

2. Theoretical basis

3. Proposed method

Vibration signal analysis is an effective means of accurately diagnosing mechanical faults and monitoring mechanical conditions, because these signals usually carry abundant state-relative information. Mine hoist is a typical item of rotating machinery used for vertical-shaft transportation, and its common fault is abnormal lifting load. Here, vibration signals are analyzed to monitor the lifting load of mine hoist. However, these vibration signals are both nonlinear and unsteady. Further, it is difficult to extract the load-relative information from these signals; thus, monitoring the lifting load of mine hoist using tradition signal processing methods is challenging. For EMD, its main purpose is to adaptively decompose a mixed signal into a series of IMFs. Theoretically, if the mixed signal is main consist of $k$ components, it can get $k$ IMFs by EMD. That is to say, EMD can get the number of components of a mixed signal. For VMD, it is also an algorithm to decompose a complex signal into its compositions with IMFs. The mode number is an important parameter for VMD and which is mean the number of the components in a complex signal. Therefore, a new signal processing approach, combined the advantages of EMD and VMD, is tentatively proposed in this paper.

SVM has been developed from statistical learning theory to solve pattern recognition and regression analysis problems using structural risk minimization principles [31, 32]; these principles can realize the optimal combination between learning precision and identification accuracy with only a small number of samples. Further, SVM-based classification can be regarded as a quadratic optimization problem. This technique first maps input samples into a particular high-dimensional space with nonlinear transformations and then finds an optimal plane for the classes in high-dimensional space to classify the input samples. In addition, SVM has stronger generalization ability than the nonlinear function approximation method, and can also overcome difficulties in determining the neural network structure and the local minimum.

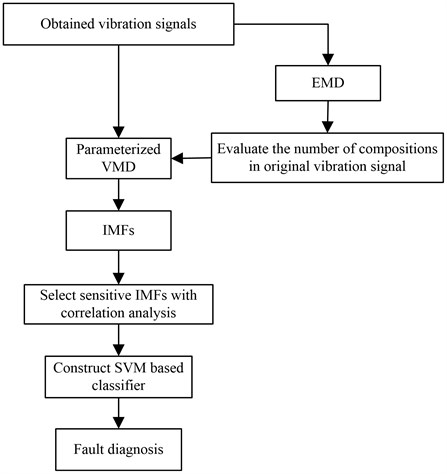
Based on the above analysis, this study presents a new condition monitoring method, based on EMD, VMD and SVM with vibration signal analysis, to precisely monitor the lifting load of mine hoist. The flow chart of the proposed method is shown in Fig. 1. First, traditional EMD is used to process the vibration signals collected by an acceleration sensor, and the number of obtained IMFs is used to set the VMD mode number. Second, the vibration signal is processed by the parameterized VMD and the useful IMFs of the VMD are selected through correlation analysis for feature extraction. Third, the obtained features are evaluated to train an SVM model, and the trained SVM is used to monitor the mine-hoist lifting load.

Fig. 1Flow chart of proposed method

4. Simulation analysis

To test the superiority of the proposed method, a simulation experiment was conducted, which is reported in this section. The test signals used in the simulation are as follows:

where $T_1=$ 1000, $T_2=\text{0.25}*i$, $i=$ 1, 2, 3, and $e\left(t\right)$ is noise that is equivalent to 0.2 times the standard deviation of the synthetic signal of $y_1$, $y_2$, and $y_3$.

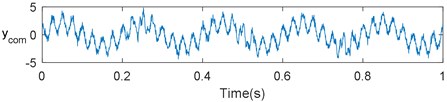
Fig. 2 shows the time-domain waves of the simulation signals, i.e., the high-frequency oscillation signal ($y_3$), low-frequency waves ($y_1$ and $y_2$), and composite signal ($y_{com}$). From this figure, the difficulty in identifying the components of the simulated $y_{com}$ is apparent. The decomposition results provided by the traditional EMD and EEMD are plotted in Fig. 3. Directly observing the plots in Fig. 3(a), it is apparent that the main components are decomposed into $c_3$ to $c_6$. From the plots in Fig. 3(b), it is apparent that most of the information on $y_1$, $y_2$, and $y_3$ is decomposed into $c_6$, $c_4$, and $c_3$. However, part of $y_1$ is falsely decomposed into IMF $c_5$, because the parameter settings are not optimal. By comparing Figs. 3(a) and (b), it is apparent that EEMD can yield a superior decomposition result for a complex signal than traditional EMD.

Fig. 2Time-domain waves of simulation signals

a)

b)

c)

d)

The above analysis reveals that traditional EMD and EEMD have certain limitations in the context of complicated signal processing, such as the mode mixing problem and the selection of optimal parameters. It has been verified that VMD, a new technique, can effectively manage complicated signals; here, it was used to decompose the composite signal shown in Fig. 2. According to the principles of the proposed method, the number of IMFs in the decomposition process of traditional EMD is 10; thus, the mode number of VMD was set to 10. Based on the results reported in [25], the balancing parameter of the data-fidelity constraint was set to 1500. Fig. 4 shows the decomposition results of the EMD-based VMD method, where $y_1$, $y_2$, and $y_3$ are successfully decomposed into the front three IMFs $c_1$, $c_2$, and $c_3$.

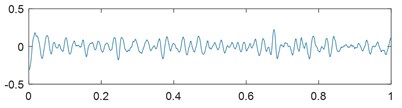
To further analyze the decomposition effect of the EMD-based VMD method, the decomposition errors of the above three simulation signals are shown in Figs. 5(a-c). Hence, we conclude that the EMD-based VMD method can effectively decompose the complicated simulated $y_{com}$ and yield superior results to the traditional EMD and EEMD.

Fig. 3Decomposition results obtained using: a) traditional EMD, b) traditional EEMD with default parameters defined in [21]

a)

b)

Fig. 4Decomposition results of the EMD based VMD

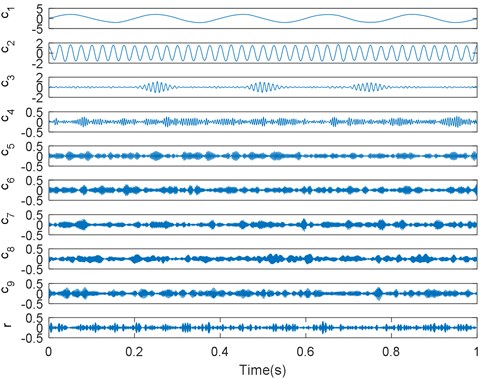
Fig. 5Decomposition errors of simulation signals: a) y1, b) y2, c) y3

a)

b)

c)

5. Experimental study

5.1. Experimental settings and data collection

To verify the efficacy of the proposed method in the context of lifting load monitoring with vibration signals, an experiment on a running mine hoist was conducted. Fig. 6 shows a schematic diagram of a multi-rope friction hoist and the data acquisition system used in this experiment. As shown in this figure, the mine hoist contained several ropes, two containers, and a main shaft apparatus. Usually, a multi-rope friction hoist is operated based on friction between ropes and pads installed in the main shaft apparatus.

Fig. 6Schematic diagram of mine hoist and data acquisition system

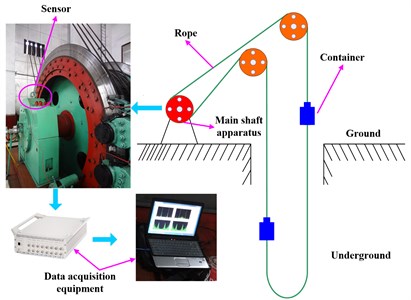
Thus, the main shaft apparatus is an important component of mine hoist, because it is not only a key transmission system of the mine hoist, but also a main load-carrying part. Therefore, the vibration signals collected from the main shaft apparatus can reveal characteristic information on the lifting load. In this work, the vibration signals were collected by the data acquisition equipment and a sensor placed on the top of the bearing housing of the main shaft apparatus with a strong magnetic foundation, as shown in Fig. 6. The data acquisition equipment included a data acquisition board and data processor, and the acquisition software system was self-developed using Visual Basic Language.

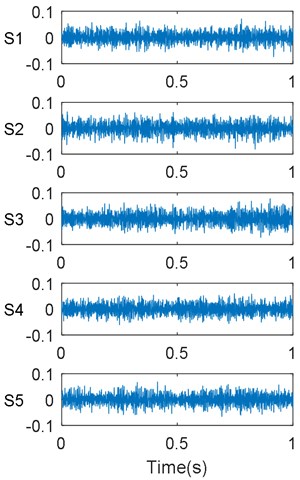
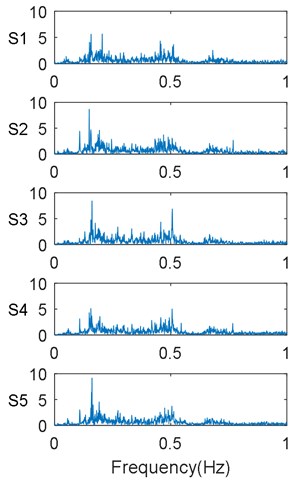
Here, five different lifting loads were simulated for the mine hoist, as listed in Table 1. The sampling frequency used to collect the vibration signals was set to 1000 Hz. Fig. 7 shows the vibration signals and their FFT spectrums for these five considered lifting load conditions. From this figure, it is apparent that some nuances exist between the amplitudes of the vibration signals obtained under different lifting load conditions. However, it is difficult to use these vibration signals directly to identify the lifting load conditions without any other obvious characteristics. Thus, features must be extracted from the collected vibration signals to reveal the information on the mine-hoist lifting load. Then, the correlations between the features and lifting load conditions can be constructed to determine if the mine hoist is operating under a normal lifting load. Recall that the main purpose of the proposed method is to facilitate monitoring and determination of the mine-hoist lifting load through vibration signal analysis alone. Further it is meaningful to determine whether the mine hoist is operating under normal or critical lifting load conditions.

Table 1Conditions of five lifting experiments

Experiment no.	Label	Lifting load (t)	Conditions
1	S1	0	No-load
2	S1	0	No-load
3	S2	8.5	Normal
4	S2	10.5	Normal
5	S3	11.6	Over load

Fig. 7Vibration signals and their FFT spectrums for considered conditions

a)

b)

5.2. Feature extraction

Feature extraction based on signal processing tools has a significant influence on condition monitoring or classification efficacy. Figs. 8, 9 show real decomposed results for the vibration signals, which were obtained using EMD, EEMD, and the proposed method. Hence, it is apparent that the condition-relative information is not decomposed from the complicated vibration signals when traditional EMD and EEMD are used. However, the first several IMFs for the EMD-based VMD method exhibit superior consistency and periodicity. That is, our method can effectively analyze the collected vibration signals.

Fig. 8Decomposition results of real vibration signals obtained using: a) traditional EMD, b) traditional EEMD with default parameters defined in [21]

a)

b)

Through use of the EMD-based VMD method, a set of IMFs can be obtained and their sensitivity for condition monitoring can be assessed. Theoretically, not all IMFs contain sufficient useful information for lifting load identification. To reduce the feature dimensions and improve the processing speed of the SVM model, a correlation analysis was conducted to quantify the usefulness of each IMF and the five most sensitive IMFs were selected to calculate permutation entropy (PE), defined in [33], as foundation features. That is, each selected vibration signal segment can product five considered IMFs and each is able to obtain one PE values, so five PE values can be calculated from each selected vibration signal segment.

However, noise commonly exits in vibration signals. To reduce the effect of noise interference on the monitoring of lifting load, we used statistical PE features, each is the mean of 15 foundation features of the same IMF, to construct samples. Therefore, in this paper, the used sample are consistent of five statistical PE features. In this work, 60 samples were extracted for each considered lifting load, 20 of which were used to train the SVM model and the remainder of which were set for testing. The used samples and target outputs of the SVM are listed in Table 2. Note that the other parameters were set to the default values given in [34].

Fig. 9Decomposition results of real vibration signals obtained using EMD-based VMD method

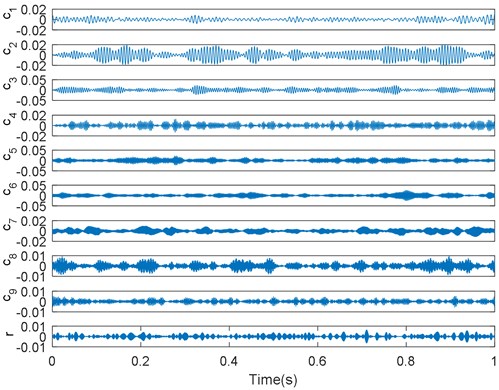
Table 2Monitoring results obtained using proposed method

Conditions	Training samples	Test samples	Target outputs
S1	20	40	1
S1	20	40	1
S2	20	40	2
S2	20	40	2
S3	20	40	3

5.3. Results and discussion

In this study, the vibration signals collected from a mine hoist under the stage of uniform motion were used to establish a correlation model between the features and lifting load conditions. Fig. 10 shows the monitoring results of the proposed method, in which the abscissa indicates the number of test samples and the ordinate expresses the outputs of the trained SVM. According to the designed SVM model, the theoretical outputs of the test samples numbered 1-80, 81-160, and 161-200 should be “1”, “2,” and “3”, respectively. From the plots in Fig. 10, only one of these outputs of the test samples numbered 1-80 is not “1”; that is to say, these test samples, except one, are identified as having a no-load condition, which is consistent with the actual situation.

Fig. 10Test results for proposed method

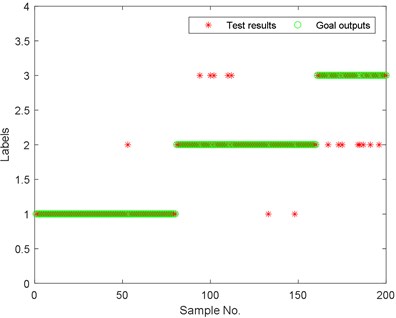
However, for the test samples numbered 81-160, some outputs are not “2”, but “1”and “3”. That is, some test samples originally corresponding to a normal load condition are mistakenly identified as corresponding to no-load conditions and overload conditions. Similar situations also appear for the test samples numbered 161-200, and some test samples are mistakenly identified as corresponding to the normal load condition. Further analysis revealed that the phenomenon in which more than two continuous adjacent test samples are mistakenly identified did not occur, and an incorrect test result for two continuous adjacent test samples occurred only once. Therefore, we can use the newest result of two or more continuous adjacent test samples as the final classification result.

To confirm the superiority of the proposed method, comparison experiments were conducted, which were labeled “SVM+EMD”, “SVM+EEMD”, and “SVM+VMD”. In these comparisons, the classifiers were all SVM models and the number of samples used to train and test the SVM model were also the same as those for the proposed method. The permutation entropy values were also all extracted from five sensitive IMFs selected via correlation analysis, and the statistical features were all calculated using 15 permutation entropy values. For the SVM+EEMD method, the EEMD was employed using the default parameters defined in [21]. For the SVM+VMD method, the mode number and balancing parameter of the data-fidelity constraint were discretionarily set to 5 and 1500, respectively. Table 3 presents the test results for these comparison methods. From this table, it is apparent that the SVM+VMD method has the worst monitoring result. That is to say, the feature extraction of SVM+VMD is not suitable as the classifier for these comparison methods are also SVM. Further analysis the monitoring results of SVM+VMD reveals that the VMD with random configuration parameters cannot decompose lifting load related information into IMFs successfully.

Table 3Monitoring results obtained using proposed method

Experiments	Training samples	Test samples	Total accuracy (%)
SVM+EMD	100	200	87
SVM+EEMD	100	200	89
SVM+VMD	100	200	81
Proposed method	100	200	92

Therefore, setting suitable mode number and balancing parameter of the data-fidelity constraint has great influence on feature extraction and condition monitoring. Further, the analysis of the monitoring results of SVM+EMD and SVM+EEMD shown that their monitoring accuracies are almost the same but are all lower than that of the proposed method. From this comparative analysis, we can conclude that the proposed method can successfully recognize the lifting load conditions of the mine hoist.

6. Conclusions

Lifting load monitoring is an effective approach to achieve a more secure operation of a mine hoist. Focusing on this issue, in this paper, a novel classification method based on variational mode decomposition (VMD) and support vector machine (SVM) through vibration signal analysis was proposed to facilitate accurate monitoring of the lifting load of mine hoist. In this work, an empirical mode decomposition (EMD)-based VMD was developed and the features of the selected sensitive intrinsic mode functions (IMFs) were extracted to construct an SVM-based classifier for monitoring the mine-hoist lifting load. Experiments on mine-hoist operation were conducted to verify the reliability and validity of the proposed method. The experimental results shown that the proposed method can accurately identify the considered lifting load conditions. Some advantages of the proposed method are the following:

1) It is difficult to directly measure the lifting load of a running mine hoist with a force transducer, because the original structure must be destroyed to install the sensor. However, vibration signals can be collected easily by installing sensors on the main shaft apparatus of the mine hoist. In this study, the mine-hoist lifting load was successfully identified by analyzing the vibration signals; thus, a new approach for lifting load monitoring was realized.

2) Complex signal processing is challenging in condition monitoring. It has been shown that VMD exhibits superior performance with respect to the processing of nonlinear and non-stationary signals compared to EMD and EEMD. However, it is difficult to preset the VMD number mode. This work presented an EMD-based VMD method to solve this problem, and the experimental results confirmed its improvement over traditional VMD.