Kinematics simulation analysis and trajectory planning of a moving robot based on ADAMS

1. Introduction

With the continuous improvement of production automation, the study of industrial robots is also constantly deepening. Zhu Hongbing [1] and others using ADAMS on a six-degree-of-freedom industrial robot simulation analysis, to obtain its displacement and velocity curve, verify the rationality of the movement model created; Zhang Baocheng [2] and others using numerical analysis software Matlab Stanford robot is used to simulate the object. Based on the kinematics of the robot, the joint displacement, velocity and acceleration curve are analyzed, and the rationality of the kinematic model is verified. ADAMS is a simulation software based on multi-body dynamics [3, 4], the use of ADAMS not only can intuitively see the movement process, but also get the corresponding displacement, velocity and acceleration curve, so the robot kinematics, kinetics analysis.

In this paper, the D-H method is used to establish a connecting rod coordinate system of six-degree-of-freedom moving robot, and its motion model is constructed. Combined with Solid works and ADAMS to simulate the moving robot, and verify the correctness of the kinematic model. At the same time, the trajectory planning of the moving robot is carried out in consideration of the actual operation of the robot. Which provides the data basis for the debugging of the six-DOF handling robot entity in practical use, and protects the handling robot to a certain extent.

2. Establishment of movement model of handling robot

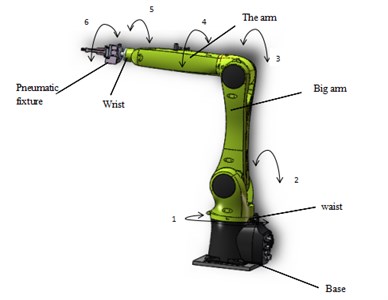
In this paper, a six-axle handling robot is designed, which consists of base, waist, arm, arm, wrist and pneumatic fixture. Among them, the pneumatic fixture fixed at the wrist end flange. This machine has six degrees of freedom: (1) Space rotation of the base (2) Space pitch of the boom (3) Space pitch of the arm (4) Space rotation of the front of the arm (5) Space pitch of the wrist (6) the space of the pneumatic fixture. The first three rotating joints determine the position of the pneumatic clamp, and the latter three turn joints determine the attitude of the pneumatic clamp. The model of the moving robot is established by the three-dimensional modeling software Solid works. Figure 1 shows the three-dimensional schematic diagram of the moving robot.

Fig. 1Schematic diagram of the overall handling of the robot

2.1. Establishment of connecting rod coordinate system

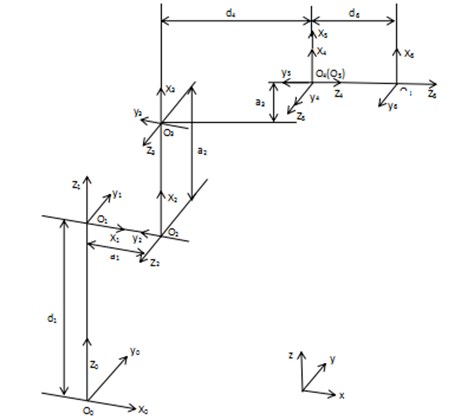
In this paper, the D-H method is used to establish the connecting rod coordinate system of the handling robot [5]. Fig. 2 shows the connecting rod coordinate system established by the six-DOF handling robot.

Fig. 2Handling robot connecting rod coordinate system

3. Simulation analysis of handling robot motion

3.1. The establishment of the model

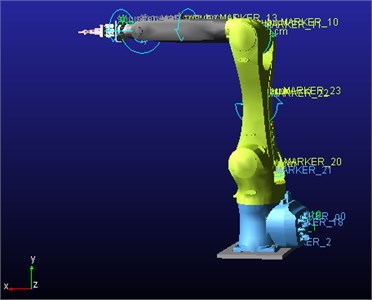
According to the kinematics model of the above-mentioned handling robot, kinematics simulation and analysis are carried out by using multi-body dynamics simulation software ADAMS. First, the three-dimensional solid model of the handling robot is built through Solid Works 3D software. To facilitate the model to open in ADAMS, save the model in parasolid ($x_t$) format [7]. Then open the ADAMS, will create the handling of the robot sub-module into. Second, add the joint constraints of the handling robot, as shown in Table 2. Fig. 3 shows the simulation model of the handling robot after adding the constraint.

Table 2Handling constraints between robot components

Sports subtype	Sports sub name	First component	Second component
Fixed vice	JOINT_0	Base	Ground
Fixed vice	JOINT_7	Pneumatic fixture	Wrist flanges
Rotate the pair	JOINT_1	Base	Waist
Rotate the pair	JOINT_2	Waist	Big arm
Rotate the pair	JOINT_3	Big arm	Forearm
Rotate the pair	JOINT_4	Forearm	Arm rear
Rotate the pair	JOINT_5	Arm rear	Wrist
Rotate the pair	JOINT_6	Wrist	Pneumatic fixture

Fig. 36-DOF handling robot simulation model

3.2. Simulation results and analysis

The end position of the pneumatic fixture is taken as the object of study, and the end position point MARKER_o6 is set on it. MARKER_o0 is established on the base as the origin of the coordinate. Set the rotation speed of each joint as shown in Table 3, the simulation time is 1s, measuring the end position relative to the base of the movement.

Table 3The angle of rotation of each joint (°) / s

JOINT_1	JOINT_2	JOINT_3	JOINT_4	JOINT_5	JOINT_6
90	30	30	90	–90	180

After the simulation, enter the post-processing interface. Fig. 4 shows the displacement of the end position relative to the origin of the link coordinate system. Fig. 5 shows the angular change of the end position relative to the origin of the link coordinate system.

It can be seen from Fig. 4, $t=$ 0 s, $O_6$ relative to $O_0$$x$ direction of the displacement is 655.0 mm, $y$ direction of the displacement is 0.0 mm, $z$ direction of the displacement is 1007.0 mm, the calculation of the two points between $x$, The relative displacement of $y$, $z$ direction is 655 mm, 0 mm, 1007 mm, the data of the two are in full agreement. When $t=$ 1 s, the displacement of $O_6$ in the $x$, $y$ and $z$ directions of $O_0$ is 116.0000, 23.5526 and 1369.3696 mm, the data of Table 3 is substituted into Eq. (2), and the displacements of $O_6$ in the $x$, $y$ and $z$ directions of $O_0$ are –116.0,23.552,1369.342 mm, respectively. The error in the $x$ direction is 0, The direction of the error is 0.00255 %, in the $z$ direction of the error is 0.00202 %, we can see that the error is very small, negligible.

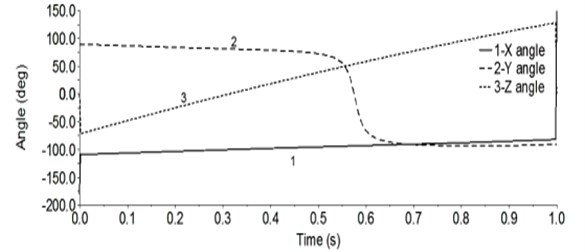
It can be seen from Fig. 5, $t=$ 0 s, $O_6$ around the $x$-axis rotation angle of –180°, around the $y$ rotation angle of 90°, around the $z$ rotation angle of 0°, that is, $O_0$ around $x$, $y$ rotation –180°, 90°, $O_6$ relative to the $O_0$ attitude is $\left[\begin{array}{lll}0& 0& 1\\ 0& -1& 0\\ 1& 0& 0\end{array}\right]$, and (2) calculated results $\left[\begin{array}{lll}0& 0& 1\\ 0& -1& 0\\ 1& 0& 0\end{array}\right]$ exactly the same; $t=$ 1 s, $O^6$ around the $x$-axis rotation angle is 150°, around the $y$-axis rotation angle is –90°, around $z$ The angle of rotation is 0°, that is, $O_0$ around $x$, $y$ rotation 150°, –90°, get $O_6$ relative to $O_0$ posture is $\left[\begin{array}{ccc}0& 0& -1\\ -0.5& -0.866& 0\\ -0.866& 0.5& 0\end{array}\right]$, and (2) calculated results $\left[\begin{array}{ccc}0& 0& -1\\ -0.5& -0.9& 0\\ -0.9& 0.5& 0\end{array}\right]$ comparison shows that the error between the two is very small, can be ignored is not small.

Fig. 4Displacement of end position point O6

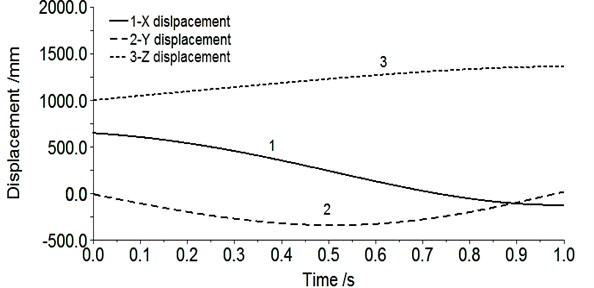
Fig. 5Angle of the end position point O6

4. Trajectory planning of handling robots

Considering the application of the moving robot in the actual production, the actual operation process of the moving robot is simulated by ADAMS. Use the STEP function in ADAMS to add the various joints of the handling robot [8, 9]. Table 4 shows the driving function of each joint, and Fig. 6 shows the trajectory of the trajectory of the pneumatic fixture at the end of the moving robot.

In the simulation environment, when the handling robot is running, there is no collision and interference between the joints, which conforms to the actual requirements of the movement. After the simulation, enter the post-processing interface.

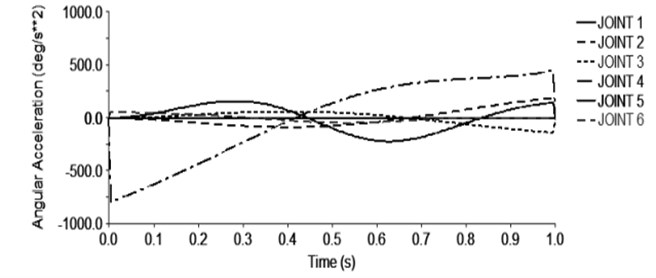
Fig. 7 shows the change of the angular velocity of each joint with time. Fig. 8 shows the change of the acceleration of each joint with time. In the trajectory planning movement of the handling robot for 7 seconds, the movement of the first few seconds is the repetition of the first 1 second movement, so only the motion angular velocity and the angular acceleration curve of the 1 second before the joint of the moving robot are intercepted. Fig. 7 shows that, as time changes, the joint angular velocity changes smoothly, where the joint 4 speed changes the largest, so the robot operation should pay special attention to the rotation of the joint 4. Figure 8 shows that the angular acceleration of each joint is not abrupt and the change is smooth. Therefore, it is known that the handling robot runs smoothly and meets the actual requirements.

Fig. 6Handling the robot end space trajectory

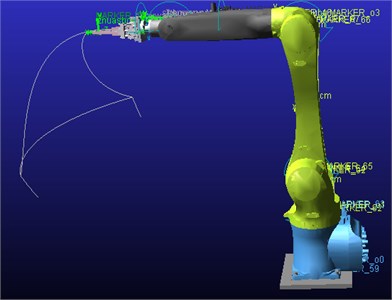
Fig. 7The speed of the joint rotation of the robot

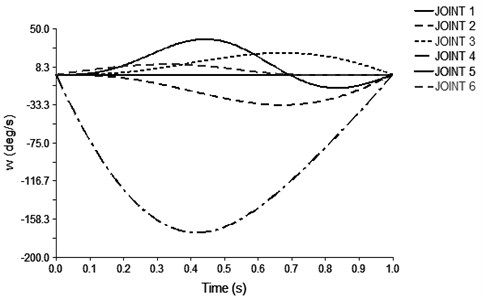
Fig. 8Handling the robot rotation angle of each joint rotation

5. Conclusion

In the automated production, the handling of industrial robots has become an indispensable tool, how effective and safe use of handling industrial robots has become a hot spot for continuous research. Using the multi-body dynamics simulation software ADAMS to simulate the movement process of the moving robot, it can not only get the corresponding speed and acceleration curve, so as to provide the basis for finding the problem and solving the problem, but also can see whether the robot has Interference and collision, reducing the physical prototype in the actual debugging damage, while saving time.