Reliability analysis of an engine under uncertainty based on D-S evidence theory and Bayesian network

Li, Zhi Qiang; Xu, Ting Xue; Gu, Jun Yuan; Fu, Lin Yu; Dong, Qi

doi:10.21595/mme.2017.19015

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 31 December 2017

Check for updates

Reliability analysis of an engine under uncertainty based on D-S evidence theory and Bayesian network

Zhi Qiang Li¹

Ting Xue Xu²

Jun Yuan Gu³

Lin Yu Fu⁴

Qi Dong⁵

^{1, 2, 3, 4, 5}Naval Aeronautical and Astronautical University, Yantai, P. R. China

Corresponding Author:

Ting Xue Xu

Cite the article Download PDF

Downloads 1368

Abstract

There are many methods applied including Bayesian network and D-S evidence theory to cope with uncertainty involving aleatory uncertainty and epistemic uncertainty in reliability analysis of complex systems. This paper introduces theories of these two methods briefly, and then conversion rules that convert fault tree into Bayesian network under uncertainty are put forward, including AND node, OR node, XOR node, NOT node and Two-out-of-three vote node. Comparing to probability importance, structural importance and criticality importance, epistemic importance is given to measure the influence of root event to top event. At last, a type of engine is taken for example. Bayesian network model is established by referring to the fault tree of the engine, and D-S evidence theory is used to determine the belief functions and plausibility functions of uncertain nodes by data fusion. Weak nodes in reliability design and distribution are pointed out after reliability assessment, importance analysis, and backward reasoning. And corresponding measures can be taken to improve the reliability of the whole system.

1. Introduction

Reliability of a system, subsystem, or unit is defined in [1] as: the ability to perform its required functions under specific operating conditions for a specified period of time. Methods of traditional reliability analysis include fault tree analysis (FTA), failure mode effect analysis (FMEA), failure mode, mechanisms and effects analysis (FMMEA), failure mode effect and criticality analysis (FMECA) and Monte Carlo sampling (MCS). Traditional research mainly centers on the assumption that system or unit has only two states, i.e., normal and failure [2]. This is appropriate for some electrical units or precise instruments. However, in reality most systems consist of units with different parameters and various failure modes. According to different classification rules of traditional analysis models, states of these units are divided into normal or fault, which leads to a loss of important information, and results in correctness decreasing of reliability analysis. The development of Bayesian network, Markov model, Petri net, and Fractional Calculus theory promotes the research of reliability analysis in multi-states of complex systems and units.

In recent years, much more attention is paid to uncertainty in reliability assessment. Uncertainty is common in the life cycle of a product. In the stage of development, uncertainty involves design scheme, reliability distribution, material choices and corresponding parameters such as failure rate, stress, strengthen and useful life. In manufacturing, uncertainty includes technological process and related technical factors such as manufacturing techniques, management level and operating skills of workers. When it comes to the period of operation, uncertainty refers to operation environment, logistics conditions and maintenance strategies and modes including posterior maintenance, scheduled maintenance and condition-based maintenance. In addition, the whole procedure involves other uncertainty, such as cost effectiveness, completion rate, economic benefit and social benefit.

Uncertainty involves two aspects, aleatory uncertainty which reflects the inherent nature of things represented by probability model and epistemic uncertainty expressing subjective judgments of human because of lack of knowledge [3, 4]. Much epistemic uncertainty information from domain experts and technicists is added into system or unit state determination, failure mode classification and original parameter setting. As systems become more complicated and sophisticated, hostile operation environment demands high reliability, long life and good characteristic, which increases costs in design, manufacturing, and logistics support, especially for airplanes, rockets and missiles. Because of variable operation environments and lacking statistical data, we should take advantage of uncertain information, incomplete information and imprecise information from original data in reliability design, testing, evaluation and prediction.

There are many methods to deal with uncertainty in reliability analysis, such as Bayes theory, convex model, reliability theory, D-S evidence theory, interval analysis, and fuzzy probability theory. In fact, aleatory uncertainty and epistemic uncertainty exit in the same complex system at the same time, so when establishing a reliability model, we should combine them together [5, 6]. Bayesian network (BN) can not only convey uncertainty and correlations between events, also describe multi-state systems and uncertain logic relationships [7-9]. In addition, BN has an advantage in reasoning forward and backward. To enhance the ability of BN in tackling uncertainty, academic literature [10] implements Bayesian network with D-S theory to treat epistemic uncertainty and extract as most information as possible from existing data. And it sets a Bayesian framework for us to utilize evidential networks without further modification. Zhao et al. [11] modified BN by D-S evidence theory to evaluating the reliability of a power distribution system containing ambiguity and uncertainty. In literature [12], the authors introduce uncertainty into FTA and assess the reliability of a type of missile engine after establishing BN model.

In this paper, we will study further in uncertainty expression and data fusion based on D-S evidence theory to assess and analyze the reliability of a complex system. In Section 2, theories of BN and D-S evidence are explained briefly. In Section 3, uncertainty is introduced into FTA, and conversion rules of converting FT nodes into BN nodes are put forward. In Section 4, a case of an engine is taken for example. By using D-S evidence theory, expert opinions are converted into belief and plausibility functions, and then dealt along with uncertain reliability values. With the advantages of BN in reasoning and importance analysis, weak node is pointed out.

2. Basic theories of BN and D-S theory

2.1. Bayesian network

Compared to FTA [13-15], BN, developed on the base of probability and graph theory, has advantages in describing events of polymorphism and expressing uncertain logic relationships. Literature [15] offers detailed introduction about BN.

BN model is denoted as $B N = (G, θ)$ . $G = (V, A)$ represents a directed acyclic graph (DAG). $V = \{V_{1}, V_{2}, \dots, V_{n}\} (n \geq 1)$ are nodes and $A$ is the set of bow. $θ$ describing CPT is denoted as $P (V_{i} | p a (V_{i}))$ . In directed edge $(V_{i}, V_{j})$ , $V_{i}$ is $V_{j}' s$ father node, and $V_{j}$ is $V_{i}' s$ child node. The set of $V_{i}' s$ father nodes can be denoted as $p a (V_{i})$ and other nodes can be denoted as $A (V_{i})$ . When $p a (V_{i})$ is obtained, $V_{i}$ and $A (V_{i})$ are conditional independent, we can get [7, 16]:

1

P (V_{i}| p a (V_{i}), A (V_{i})) = P (V_{i}| p a (V_{i})) .

And the joint probability of BN can be denoted as:

2

P (V_{1}, V_{2}, \dots, V_{k}) = \prod_{i = 1}^{k} P (V_{i}| V_{i - 1}, V_{i - 2}, \dots, V_{1}) = \prod_{i = 1}^{k} P (V_{i} | p a (V_{i})) .

2.2. D-S evidence theory

D-S evidence theory is put forward by Dempster in 1967, and then modified by his student Shafer, so it’s also called Dempster Shafer theory.

The frame of discernment $Θ$ is the set of disjoint states or focal elements of $X$ . The function is defined as [17, 18]: $m : 2^{Θ} \to [0,1]$ verifying:

3

m (θ) = 0,

4

\sum_{A \subset Θ} m (A) = 1,

where $m (A)$ is the basic probability assignment (BPA) on the frame of discernment $Θ,$ representing the supporting degree of evidence to event $A .$

In D-S evidence theory, plausibility and belief functions play a role in gaining system failure information. The belief function is defined as $b e l$ : $2^{Θ} \to [0,1]$ , $\forall A \subset Θ$ by:

5

B e l (A) = \sum_{B \subset A} m (B) .

While the plausibility function is defined as $p l s$ : $2^{Θ} \to [0,1]$ , $\forall A \subset Θ$ , by:

6

P l (A) = 1 - B e l (\bar{A}) = \sum_{B \cap A \neq \emptyset} m (B) .

The belief and plausibility functions determine the bounding of the probability, then:

7

B e l (A) \leq P (A) \leq P l (A) .

According to the compositional rule of Dempster, for $n$ mass functions $m_{1}$ , $m_{2}$ , …, $m_{n}$ on the frame of discernment $Θ$ , we can obtain:

8

m (C) = \{\begin{array}{l} \begin{array}{l} \frac{\sum_{A_{i} \cap B_{j} \cap \dots \cap Z_{k} = C} m (A_{i}) \cdot m (B_{j}) \cdot \dots \cdot m (Z_{k})}{1 - K}, & \forall C \subset Θ, C \neq \emptyset . \end{array} \\ \begin{array}{l} 0, & C = \emptyset . \end{array} \end{array}

$K$ is the coefficient of friction between the evidence, denoted as:

9

K = \sum_{A_{i} \cap B_{j} \cap \dots \cap Z_{k} = \emptyset} m (A_{i}) \cdot m (B_{j}) \cdot \dots \cdot m (Z_{k}) < 1 .

3. Modifying Bayesian network with D-S evidence theory

3.1. BN node model under uncertainty

The main problem in constructing a Bayesian network model including establishing the topological structure and calculating the probability parameters, is knowledge acquisition. By so far, there are three methods in building a Bayesian network model. 1) By consulting experts in related domain and using experts’ experience knowledge, we can establish a Bayesian network model manually, and get CPT given by experts. 2) By using computers to reason from a large amount of data from the database, a Bayesian network model can be established automatically, and CPT can be obtained automatically. 3) Construct a Bayesian network model in two phases. By this method, a Bayesian network model is established in the circumstance of experts’ knowledge, and CPT is also given by experts. Then, the model is modified by the information in the database. In relatively, for some complex systems, especially new systems, information is so scarce that we can establish fault tree according to its inner structure, operation principle, failure mode and then convert it into Bayesian network model on the basis of failure mechanism analysis. Compared with traditional reliability analysis methods, BN model reduces the procedure of calculating minimal cut sets or minimal path sets, and bottom events appearing for more than one time can be denoted by one node.

In reliability analysis of complex systems under uncertain conditions, $E =$ 0 is used to represent fault and $E =$ 1 for normal, then $E = {0,1}$ denotes the uncertainty. In other words, an uncertain state is added to traditional binary state fault tree. In reliability analysis model, the frame of discernment is $Θ = {0,1}$ , if $m : 2^{Θ} \to [0,1]$ is the basic probability assignment function, the power set is:

10

2^{Θ} = \{m (E = \emptyset) = 0; m (E = \{1\}); m (E = \{0\}); m (E = \{0,1\})\} .

Basic probability assignment function is limited by Eqs. (3) and (4). Focal element ${0,1}$ represents that reliability analysis experts do not know whether event $E$ happens or not, which denotes the uncertainty. Fig. 1 shows the conversion process of AND node in fault tree into BN node. The state of top event $T$ is determined by bottom events $E_{1}$ and $E_{2}$ . Due to uncertainty, the top event $T$ will happen definitely only when bottom events $E_{1}$ and $E_{2}$ happen. If one of the bottom events does not happen, the top event $T$ will not happen. In other cases, it is uncertain whether top event $T$ will happen or not. According to the rules of logical gate of OR node, XOR node, NOT node and Two-out-of-three voting node, corresponding nodes in BN model under uncertain conditions are determined, shown in Fig. 2-5.

Fig. 1AND node in BN model

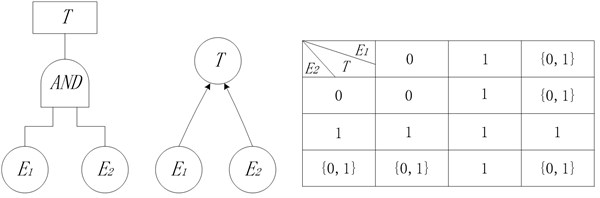
Fig. 2OR node in BN model

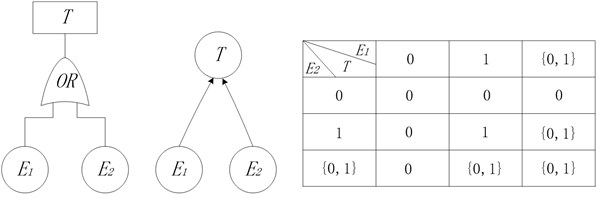
Fig. 3XOR node in BN model

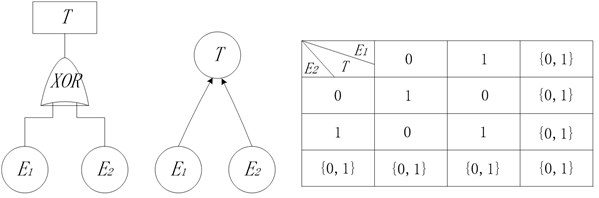
Fig. 4NOT node in BN model

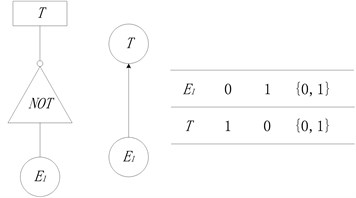
Fig. 5Two-out-of-three node in BN model

3.2. Modeling procedure

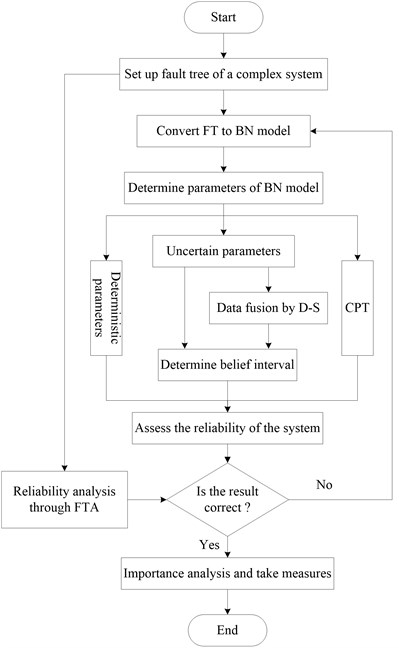
Data information from different sources can be fused through D-S evidence theory. And by taking use of the advantages of BN in uncertainty expression and reasoning, modified model of BN is established on the basis of data fusing. Firstly, by consulting experts and resourcing, fault tree of complex system is set, and according to conversion rules mentioned above, BN model is established. Secondly, determine parameters including deterministic parameters and uncertain parameters and CPT of BN model. For parameters having only one data source, belief and plausibility functions can be determined directly by D-S evidence theory. For parameters having lots of data sources, the compositional rule of Dempster is applied to data fusion, belief and plausibility functions are determined according to uncertain parameters. Thirdly, assess the reliability of complex system using parameters determined, and compare the result with value obtained through traditional reliability analysis to judge the correctness of BN model. If the result is not satisfied, adjust the nodes or modify the parameters. Lastly, find weak node through importance analysis and then take some corresponding measures. The modeling procedure is shown in Fig. 6.

3.3. Importance analysis

By Bucket elimination algorithm, it’s easy to calculate three kinds of importance indexes of bottom event $E_{i}$ in BN model.

1) Probability importance:

11

I_{i}^{P r} = P (T = 0| E_{i} = 0) - P (T = 0| E_{i} = 1) .

2) Structural importance:

12

I_{i}^{S t} = P (T = 0| E_{i} = 0, P (E_{j} = 0) = 0.5) - P (T = 0| E_{i} = 1, P (E_{j} = 0) = 0.5),

where $1 \leq j \neq i \leq N$ .

3) Criticality importance:

13

I_{i}^{C r} = \frac{P (E_{i} = 0) \cdot (P (T = 0 | E_{i} = 0) - P (T = 0 | E_{i} = 1))}{P (T = 0)} = \frac{P (E_{i} = 0)}{P (T = 0)} \cdot I_{i}^{P r} .

Because of the existing of uncertainty, the bottom event $E_{i}$ has three states, i.e., $E_{i} = {1}$ , $E_{i} = {0}$ , $E_{i} = {0,1}$ . Except the structural importance is a constant, the other two are interval values. So, we can define the mean value of the belief and plausibility functions as their constant value:

14

P (\cdot) = (B e l (\cdot) + P l (\cdot)) / 2

4) Epistemic importance.

To reflect the influence of uncertainty on system reliability assessment comprehensively, epistemic importance is put forward. Epistemic importance is an index to measure the influence of epistemic uncertainty in bottom event on the uncertainty of top event, which is defined as the difference value between belief function and plausibility function of top event when the epistemic uncertainties of other bottom events are 0:

15

\begin{array}{l} I_{i}^{E p} = P l (T = 0| c o n d .) - B e l (T = 0| c o n d .), \\ c o n d . : m (E_{i} = \{0,1\}) \neq 0, m (E_{j} = {0,1}) = 0, \end{array}

where $i = 1,2, \dots, n$ , $j = 1,2, \dots, n$ , $j \neq i .$

Fig. 6Modeling procedure of BN model modified by D-S theory

4. A case study

4.1. Setting up a fault tree

A certain type of engine consists of two electric detonators, an ignition signal, a seal ring, a power grain and the shell [12]. Because of its complex structure, a fault tree model is set up, shown in Fig. 7, based on the logical relationship of series-parallel connection which reflects the function of system and all parts and their interactional relationship. Details of events are listed in Table 1.

Fig. 7Fault tree of a type of engine

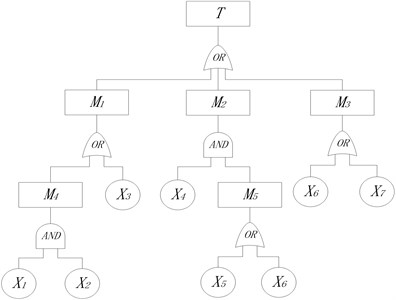
Table 1Details of events in fault tree

Event	Meaning
$T$	Failure of engine
$M_{1}$	Failure of ignition
$M_{2}$	Explosion of shell
$M_{3}$	Burning through of shell
$M_{4}$	Failure of electric detonators
$M_{5}$	Too high of pressure
$X_{1}$	Failure of electric detonator 1
$X_{2}$	Failure of electric detonator 2
$X_{3}$	Failure of ignition signal
$X_{4}$	Failure of shell
$X_{5}$	Crack of grain
$X_{6}$	Debonding of coating layer
$X_{7}$	Failure of seal ring

Obviously, the minimal cut sets of fault tree of the engine are ${X_{1}, X_{2}}$ , ${X_{3}}$ , ${X_{4}, X_{5}}$ , ${X_{6}}$ and ${X_{7}} .$ So the failure rate of top event is determined by:

16

P (T) = P (k_{1} \cup k_{2} \cup \dots \cup k_{N_{k}}) = \sum_{i = 1}^{N_{k}} P (k_{i})

- \sum_{i < j = 2}^{N_{k}} P (k_{i} k_{j}) + \dots + (- 1)^{N_{k} - 1} P (k_{1} k_{2} \dots k_{N_{k}}) .

4.2. Building up BN model

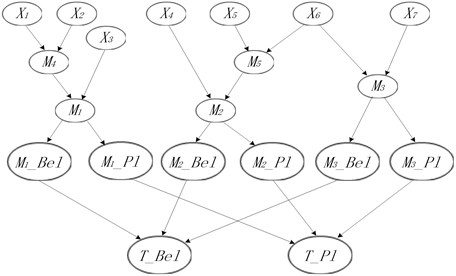
According to conversion rules introduced in Section 4, BN model of the engine is established by using software GeNIe 2.0, shown in Fig. 8.

Taking no account of uncertainty, the probabilities of intermediate nodes and top event can be calculated as follow:

17

P (M_{4} = 0) = \sum_{X_{1}, X_{2}, M_{4}} P (X_{1}, X_{2}, M_{4}) = \sum_{X_{1}} P (X_{1}) \sum_{X_{2}} [P (M_{4}| X_{2}) \cdot P (X_{2})]

= P (X_{1} = 0) \cdot P (X_{2} = 0),

18

\begin{array}{l} P (M_{5} = 0) = \sum_{X_{5}, X_{6}, M_{5}} P (X_{5}, X_{6}, M_{5}) = \sum_{X_{5}} P (X_{5}) \sum_{X_{6}} [P (M_{5}| X_{6}) \cdot P (X_{6})] \\ = 1 - [1 - P (X_{5} = 0)] \cdot [1 - P (X_{6} = 0)], \end{array}

19

P (M_{3} = 0) = \sum_{X_{6}, X_{7}, M_{3}} P (X_{6}, X_{7}, M_{3}) = 1 - [1 - P (X_{6} = 0)] \cdot [1 - P (X_{7} = 0)],

20

P (M_{2} = 0) = \sum_{X_{4}, M_{5}, M_{2}} P (X_{4}, M_{5}, M_{2}) = P (X_{4} = 0) \cdot P (M_{5} = 0),

21

P (M_{1} = 0) = \sum_{M_{4}, X_{3}, M_{1}} P (M_{4}, X_{3}, M_{1}) = 1 - [1 - P (M_{4} = 0)] \cdot [1 - P (X_{3} = 0)],

22

P (T = 0) = \sum_{M_{1}, M_{2}, M_{3}, T} P (M_{1}, M_{2}, M_{3}, T) = 1 - [1 - P (M_{1} = 0)]

\cdot [1 - P (M_{2} = 0)] \cdot [1 - P (M_{3} = 0)] .

When uncertainty exists, uncertain information will propagate from bottom events to top event through intermediate nodes [19]. Inputs of bottom events will be converted into interval values containing uncertainty, and the probabilities of intermediate nodes and top event will be determined by belief and plausibility functions. For top event, we can get:

23

B e l (T = 1) \leq P (T = 1) \leq P l (T = 1) .

Fig. 8BN model of an engine

4.3. Uncertain data processing

By referring to related documents, failure rates of $X_{1}$ , $X_{2}$ , $X_{4}$ , $X_{5}$ and $X_{6}$ at a given time are obtained as follows: $P (X_{1} = 0) =$ 0.080, $P (X_{2} = 0) =$ 0.080, $P (X_{4} = 0) =$ 0.025, $P (X_{5} = 0) =$ 0.050, $P (X_{6} = 0) =$ 0.008-0.016. Because of lacking failure rates of $X_{3}$ and $X_{7}$ , so we consult two experts with rich experience in their domain respectively to determine the relationships between bottom events and intermediate events, shown in Table 2. According to the causal relationships between bottom events and intermediate events, there are only three logical links, i.e., $A_{1}$ (Failure of bottom event leads to failure of intermediate event.), $A_{2}$ (Failure of intermediate event is not relevant to failure of bottom event.), $A_{3}$ (The relationship between failure of bottom event and failure of intermediate event is uncertain.). And these three links make up the frame of discernment $Θ .$

Because we cannot use information from experts directly, so D-S evidence theory should be applied to fuse experts’ suggestions. Fuse data from Expert 1 and 2 according to Eqs. (8) and (9), we obtain:

K = 0.0620, m (A_{1}) = 0.9840, m (A_{2}) = 0.0075, m (A_{3}) = 0.0085 .

Similarly, from Expert 3 and 4, we obtain:

K = 0.0272, m (A_{1}) = 0.9901, m (A_{2}) = 0.0027, m (A_{3}) = 0.0072 .

Table 2Collection of expert suggestions

$X_{3}$	$A_{1}$	$A_{2}$	$A_{3}$
Expert 1	0.90	0.02	0.08
Expert 2	0.85	0.05	0.10
$X_{7}$	$A_{1}$	$A_{2}$	$A_{3}$
Expert 3	0.88	0.02	0.10
Expert 4	0.92	0.01	0.07

4.4. Reliability assessment of the engine

In BN model, inputs of node $X_{1}$ , $X_{2}$ , $X_{4}$ and $X_{5}$ are deterministic values, and the inputs of other three nodes are mean values of belief and plausibility functions. By inferring to Eqs. (16) and Eqs. (17)-(22) respectively, we obtain the same result: $P (T = 0) = 0.03717$ .

When uncertainty of root nodes is taken into consideration, probabilities of belief and plausibility functions of intermediate nodes and leaf node are calculated according to Eqs. (5) and (6), shown in Table 3. Because the failure rate of engine with deterministic inputs is 0.03717, while $P (T = 0) \in [0.02560,0.04866]$ , we can make a conclusion that Bayesian network model is correct.

Table 3Probability values of intermediate nodes and leaf node

Node	$B e l$ ( $M =$ 0) (×10^-2)	$P l$ ( $M =$ 0) (×10^-2)
$M_{1}$	1.3852	2.2298
$M_{2}$	0.1440	0.1630
$M_{3}$	1.0678	2.5742
$M_{4}$	0.6400	0.6400
$M_{5}$	5.7600	6.5200
$T$	2.5602	4.8656

According to Eqs. (11)-(14), importance indexes including probability importance, structural importance and criticality importance of root nodes are obtained, shown in Table 4 and Fig. 9. In order to make a comparison, we assure:

P (X_{1} = 0) \in [0.070,0.090], P (X_{2} = 0) \in [0.070,0.090],

P (X_{4} = 0) \in [0.020,0.030], P (X_{5} = 0) \in [0.040,0.060] .

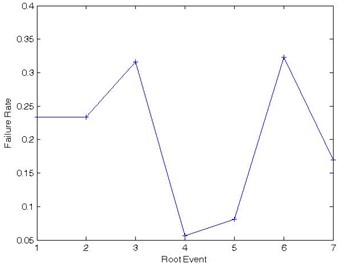
So the epistemic importance is calculated as follow according to Eqs. (15). From Table 4, we can see that probability importance and structural importance of $X_{3}$ , $X_{6}$ , $X_{7}$ are very high, because they are in OR nodes in BN model. That is to say, their reliability values affect that of the whole system directly. As to criticality importance values, except for these three events, $X_{1}$ and $X_{2}$ are included. Although uncertainties of $X_{3}$ , $X_{6}$ and $X_{7}$ are relatively lower, their epistemic importance are high than the other four events. Also, we can make a conclusion that the uncertainty is not related closely to the epistemic importance, so the uncertainty of an event cannot reflect its influence on the whole system. Assuming the engine is in failure, we can obtain the conditional probabilities of root events by backward reasoning with BN, shown in Fig. 9. Obviously, failure rate of event 3 and 6 are higher than the other events reaching 0.3167 and 0.3228 respectively. So $X_{3}$ and $X_{6}$ are weak nodes, and in reliability design and distribution, we should take them into consideration firstly. Of course, $X_{1}$ , $X_{2}$ and $X_{7}$ are important too, their reliability indexes also need our attention.

Table 4Results of importance analysis

Event	Uncertainty	$I_{i}^{P r}$	$I_{i}^{S t}$	$I_{i}^{C r}$	$I_{i}^{E p}$ (×10^-2)
$X_{1}$	0.0200	0.0775	0.0469	0.1668	0.1550
$X_{2}$	0.0200	0.0775	0.0469	0.1668	0.1550
$X_{3}$	0.0085	0.9743	0.1406	0.3080	0.8281
$X_{4}$	0.0100	0.0482	0.0469	0.0324	0.0482
$X_{5}$	0.0200	0.0241	0.0469	0.0324	0.0482
$X_{6}$	0.0080	0.9745	0.1406	0.3146	0.7796
$X_{7}$	0.0072	0.9689	0.1406	0.1642	0.6976

Fig. 9Importance analysis results

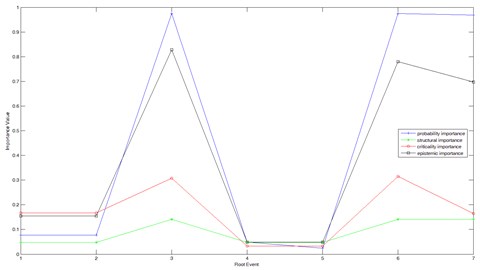
Fig. 10Failure rates of root events when system in failure

5. Conclusions

As a traditional reliability analysis method, fault tree analysis costs a lot of time and is easy to cause human errors when determining minimal cut sets or minimal path sets. Instead, Bayesian network has an advantage in establishing reliability analysis model precisely and clearly. With the using of special software such as MSBNX, BNT, Netica, BayesiaLab, GeNIe (applied in this paper), we can obtain the reliability values of the system and related nodes, and calculate the importance indexes of corresponding nodes. When uncertain data is taken into consideration, we should modify our model to deal with interval values or fuzzy values. At this moment, D-S evidence theory is good choice, especially when uncertain data has different sources, such as from different experts’ experiences. It provides a powerful tool to tackle uncertain information in data fusion, and express uncertain relationships between units and system when introduced into Bayesian network. Of course, D-S evidence theory may have the problem of conflict coefficient friction between the evidence in data fusion which need to improve in further work. Corresponding measures should be taken according to reliability assessment results to improve the reliability of the whole system, such as distributing a high reliability value to weak nodes in design, checking and testing performance parameters of weak nodes at a constant interval, maintaining a favorable storage environment.

References

Rania H., William C. Spacecraft reliability-based design optimization under uncertainty including discrete variables. Journal of Spacecraft and Rockets, Vol. 45, Issue 2, 2008, p. 394-405.

Publisher
Mangey R., Singh S. B. Analysis of a complex system with common cause failure and two types of repair facilities with different distributions in failure. International Journal of Reliability and Safety, Vol. 4, Issue 4, 2010, p. 381-392.

Publisher
Aven T., Nokland T. E. On the use of uncertainty importance measures in reliability and risk analysis. Reliability Engineering and System Safety, Vol. 95, 2010, p. 127-133.

Publisher
Aven T. Interpretations of alternative uncertainty representations in a reliability and risk analysis context. Reliability Engineering and System Safety, Vol. 96, 2011, p. 353-360.

Publisher
Yao W., Chen X. Q., Huang Y. Y., Michel V. T. An enhanced unified uncertainty analysis approach based on first order reliability method with single-level optimization. Reliability Engineering and System Safety, Vol. 116, 2013, p. 28-37.

Publisher
Zhao Y., Fan F., Wang Jie, Xie K. G. Uncertainty analysis for bulk power systems reliability evaluation using Taylor series and nonparametric probability density estimation. Electrical Power and Energy Systems, Vol. 64, 2015, p. 804-814.

Publisher
Alyson G. W., Christine M. A. C., Aparna V. H. A case study for quantifying system reliability and uncertainty. Reliability Engineering and System Safety, Vol. 96, 2011, p. 1076-1084.

Publisher
Sankaran M., Zhang R. X., Natasha S. Bayesian networks for system reliability reassessment. Structural Safety, Vol. 23, 2001, p. 231-251.

Publisher
Helge L., Luigi P. Bayesian networks in reliability. Reliability Engineering and System Safety, Vol. 92, 2007, p. 92-108.

Publisher
Simona C., Weber P., Evsukoff A. Bayesian networks inference algorithm to implement Dempster Shafer theory in reliability analysis. Reliability Engineering and System Safety, Vol. 93, 2008, p. 950-963.

Publisher
Zhao S. Q., Cheng D. C., Liu L. Reliability evaluation of power distribution system based on D-S evidence inference and Bayesian networks method. Transaction of China Electrotechnical Society, Vol. 24, Issue 7, 2009, p. 134-138.

Search CrossRef
Suo B., Zeng C., Cheng Y. S., Li J. Reliability analysis based on evidence theory and Bayesian network method. Systems Engineering and Electronics, Vol. 33, Issue 10, 2011, p. 2343-2347.

Search CrossRef
Gert De C. On modeling possibilistic uncertainty in two-state reliability theory. Fuzzy Sets and Systems, Vol. 83, 1996, p. 215-238.

Publisher
Alyson G. W., Aparna V. H. Bayesian networks for multilevel system reliability. Reliability Engineering and System Safety, Vol. 92, 2007, p. 1413-1420.

Publisher
Li Z. Q., Gu Dong J. Y. Q., Xu T. X. Assessment of complex system reliability based on FTA-BN method. Proceeding of 23th International Conference on Mechatronics and Machine Vision in Practice, 2016.

Publisher
Niloofar P., Ganjali M., Rohani M. R. F. Improving the performance of Bayesian networks in non-ignorable missing data imputation. Kuwait Journal of Science, Vol. 40, Issue 2, 2013, p. 83-101.

Search CrossRef
Khalaj M., Makui A., Tavakkoli Moghaddam R. Risk-based reliability assessment under epistemic uncertainty. Journal of Loss Prevention in the Process Industries, Vol. 25, 2012, p. 571-581.

Publisher
Guan X., Sun G. D., Guo Q., He Y. Radar emitter parameter recognition based on interval number and evidence theory. Systems Engineering and Electronics, Vol. 36, Issue 7, 2014, p. 1269-1274.

Search CrossRef
Claudio M. R. S., José E. R. M. Uncertainty propagation and sensitivity analysis in system reliability assessment via unscented transformation. Reliability Engineering and System Safety, Vol. 132, 2014, p. 176-185.

Publisher

About this article

Received

09 August 2017

Accepted

11 September 2017

Published

31 December 2017

DOI

https://doi.org/10.21595/mme.2017.19015

Keywords

uncertainty

D-S evidence theory

Bayesian network

fault tree

importance analysis

Acknowledgements

This work is supported by National Natural Science Foundation of China (No. 51605487).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Review article

2023 11 04

A comprehensive review of mechanical fault diagnosis methods based on convolutional neural network

Junjian Hou, Xikang Lu, Yudong Zhong, Wenbin He, Dengfeng Zhao, Fang Zhou

Research article

2022 12 23

Reliability calculation with error tree analysis and breakdown effect analysis for a quadcopter power distribution system

Kazem Imani, Amirhossein Gholami, Mahdi Bagherian Dehaghi

Research article

2022 10 22

Health diagnosis of marine engine room equipment based on BP and D-S evidence theory

Yuhang Jiang, Zhimin Wang, Yi Zhang, Ning Chen

Research article

2022 04 21

Thermal fault diagnosis of marine diesel engine based on LSTM neural network algorithm

Yu Zhao, Shuheng Wang, Ning Chen

Z. Q. Li, T. X. Xu, J. Y. Gu, L. Y. Fu, and Q. Dong, “Reliability analysis of an engine under uncertainty based on D-S evidence theory and Bayesian network,” Mathematical Models in Engineering, Vol. 3, No. 2, pp. 78–88, Dec. 2017, https://doi.org/10.21595/mme.2017.19015

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/mme.2017.19015
UR  - https://doi.org/10.21595/mme.2017.19015
TI  - Reliability analysis of an engine under uncertainty based on D-S evidence theory and Bayesian network
T2  - Mathematical Models in Engineering
AU  - Xu, Ting Xue
AU  - Li, Zhi Qiang
AU  - Gu, Jun Yuan
AU  - Fu, Lin Yu
AU  - Dong, Qi
PY  - 2017
DA  - 2017/12/31
PB  - JVE International Ltd.
SP  - 78-88
IS  - 2
VL  - 3
SN  - 2351-5279
SN  - 2424-4627
ER  - 

Copy Ris

Copied to clipboard!

@article{Xu_2017,
	doi = {10.21595/mme.2017.19015},
	url = {https://doi.org/10.21595/mme.2017.19015},
	year = 2017,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {3},
	number = {2},
	pages = {78--88},
	author = {Ting Xue Xu and Zhi Qiang Li and Jun Yuan Gu and Lin Yu Fu and Qi Dong},
	title = {Reliability analysis of an engine under uncertainty based on D-S evidence theory and Bayesian network},
	journal = {Mathematical Models in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]T. X. Xu, Z. Q. Li, J. Y. Gu, L. Y. Fu, and Q. Dong, “Reliability analysis of an engine under uncertainty based on D-S evidence theory and Bayesian network,” Mathematical Models in Engineering, vol. 3, no. 2, pp. 78–88, Dec. 2017, doi: 10.21595/mme.2017.19015.

Copy IEEE

Copied to clipboard!

Xu, Ting Xue, Zhi Qiang Li, Jun Yuan Gu, Lin Yu Fu, and Qi Dong. “Reliability Analysis of an Engine under Uncertainty Based on D-S Evidence Theory and Bayesian Network.” Mathematical Models in Engineering 3, no. 2 (December 31, 2017): 78–88. https://doi.org/10.21595/mme.2017.19015.

Copy Chicago

Copied to clipboard!

Reliability analysis of an engine under uncertainty based on D-S evidence theory and Bayesian network

Abstract

1. Introduction

2. Basic theories of BN and D-S theory

2.1. Bayesian network

2.2. D-S evidence theory

3. Modifying Bayesian network with D-S evidence theory

3.1. BN node model under uncertainty

3.2. Modeling procedure

3.3. Importance analysis

4. A case study

4.1. Setting up a fault tree

4.2. Building up BN model

4.3. Uncertain data processing

4.4. Reliability assessment of the engine

5. Conclusions

References

About this article

Related Articles