Study on new method for modal parameters identification of stiffened plate with four clamped edges

1. Introduction

In order to improve rigidity and strength of plate, stiffened plate structure is wide used in industrial fields specially in the aerospace, shipbuilding and automobile industry. This structure has the advantages of light weight and high stiffness [1]. Therefore, in order to better understand the characteristics of the stiffened plate, it is necessary to analyze the vibration characteristics of stiffened plate.

At present, its results are seldom about the vibration analysis of the stiffened plate, and most of the results focus on FEM (Finite Element Method) software and experiment Method, the numerical method of stiffened plate is rare analyzed. Cho [2] proposed a method based on FEM and the assumed modal for the inherent modal analysis of stiffened plate structure, but there are still some deficiencies in this research of using FEM software methods, such as the serious distortion if the inappropriate element and mesh are selected. Liu [3] developed a method to study influence of the different arrangement forms of the stiffened rib for vibration of stiffened plate, Qiu [4] presented a method for the ultimate strength research for two-way orthogonal stiffened plate. Laser method, sweeping method of frequency, tapping method are frequent used in experiment, Li Xiao-jun [5], Li Shengquan [6], Hu Yuyong [7] respectively used sweeping method, laser method, tapping method to analyze vibration natural frequency of the stiffened structures. Although experimental method is relatively accurate, it is required the sensor of the reception test data pasted accurately, however, it is not easy that the sensor will be pasted on the appropriate location. For numerical method, Zhou [8] proposed a method based on analysis of stiffened plate structure of the difference method, N. Nguyen-Minh [9] developed a method to research free vibration of folded plate by cell smooth discrete shear gap, Zhong Ming [10] studied the rectangular plates from angle of theory, Ma Niujing [11] presented a analytical method of Lagrange equation for nonlinear free vibration of stiffened plate with four edges clamped. However, the reports of piezoelectric stiffened plates show that the calculating process of numerical calculation method could be often more complicated.

In view of these, Rayleigh-Ritz method was used to simplify numerical calculation of frequency analysis problem for the stiffened plate in this paper. Relative to other numerical methods, the Rayleigh-Ritz method is applied to the modeling of frequency analysis problem creatively. It makes the calculation process of the model simplified greatly. At the meantime, it can guarantee the correctness of the analysis process and provide theoretical basis for the engineering application and contrast of experimental analysis.

2. Vibration equation of stiffened plate

Stiffened plate structure is shown as Figs. 1-2, where $a$, $b$, $h$ respective represent the length, width and height of stiffened plate structure, width and height of stiffened plate structure, $w(x,y,t)$ is neutral flexural function of the stiffened plate.

Fig. 1Structure of stiffened plate

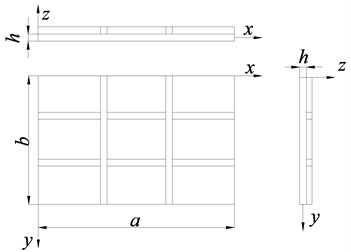
Fig. 2Reinforced bar structure

Considering the nonlinear plate, the reinforced bar can be equivalent to Euler beam element [11], then the deformation energy of the reinforced bars can be expressed respectively:

where $i=\mathrm{1,2},\dots ,Nx$, $j=\mathrm{1,2},\dots ,Ny$, $E{I}_x$, $E{I}_y$ – bending rigidity.

The kinetic energy of the reinforced bars can be expressed respectively:

Based on Rayleigh-Ritz method:

where $U_m=U+u_{x_i}+u_{y_i}$, $T_m=T+T_{x_i}+T_{y_i}$.

3. Analysis for stiffened plate by ANSYS and experiment

3.1. ANSYS analysis for stiffened plate

Unit type of the plate is Shell63, density of unit is 2700 kg/m³, elastic modulus is 72e9 Pa, Poisson’s ratio is 0.3. Through the horizontal and vertical line segment to form unit grid, the modal analysis results are shown as Fig. 3-4.

Fig. 3First mode of stiffened plate

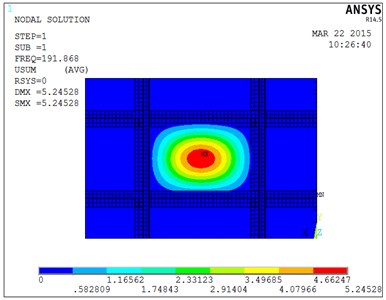
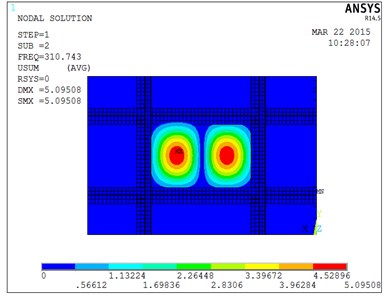
Fig. 4Second mode of stiffened plate

3.2. Experiment analysis for stiffened plate

Experimental system is showed as Fig. 5. Under sinusoidal sweep excitation signal of 0-500 Hz, piezoelectric acceleration sensor collected time domain signal as Fig. 6(a), then Fig. 6(b) is frequency spectrum analysis of Fig. 6(a).

Fig. 5The experimental system

Fig. 6Frequency domain graph

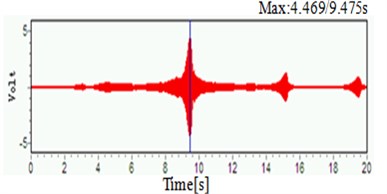
a) The time domain figure

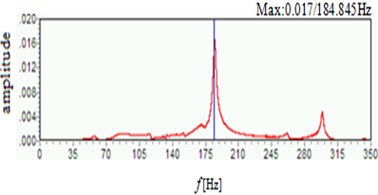
b) Frequency domain graph

Natural frequency results of the stiffened plate are shown in Table 2, these results include theoretical calculation, ANSYS analysis, experiment test three ways.

Table 2 shows that results from ANSYS and experimental would be bigger compared with theoretical calculation results, the main reason is that the impact on natural frequency of stiffened plate by smaller torsional rigidity could be ignored in order to simplify the complex calculation process [12-13]. Experimental results are also small compared with the ANSYS results, the main reason is that the boundary of the stiffened plate fixation couldn’t be fixed completely in the experiment. however, the ANSYS analysis process is the ideal conditions in boundary completely fixed.

Table 2Natural frequency of stiffened plate

Item	The first modal frequency (Hz)	The second modal frequency (Hz)
Theory	181.65	295.16
ANSYS	191.87	310.74
Experiment	184.845	298.795

4. Conclusions

The natural frequency of stiffened plates with four edges clamped is solved by Rayleigh-Ritz method. Its results compared with results of ANSYS and experiment showed that theoretical derivation from Rayleigh-Ritz method is correctness. Compared with other theoretical calculation methods, its calculation process is relatively simple. Rayleigh-Ritz method is appropriate for the theoretical calculation of the stiffened plate. It offers a new method for the frequency analysis of the stiffened plate, which avoids the high requirements for engineering experience and theoretical basis in the FEM analysis. Meanwhile, it offers contrast of result for the result of the experiment, and it also provides support for further nonlinear vibration active control experiment research.