Research on natural frequency of structure considering elastic joint with interval uncertainty

1. Introduction

In pace with the rapid development of science and technology, the engineering structure is increasingly complex, and there are more and more elastic joints existing in these complex structure [1]. In general, both the material and dimension parameters of the elastic joint hold interval uncertainty [2, 3]. As a consequence, for obtaining more accurate vibration properties of the increasingly complex structure, the interval uncertainty of the elastic joint should be taken into consideration.

Fixed interface mode synthesis method (FIMSM), initially proposed by Hurty [4], is an efficient way to analyze the dynamic properties of large-scale complex structure. In reference [5], via using generalized spring to simulate the elastic joint, the dynamic properties of structure considering elastic joint is preliminarily investigated according to FIMSM. Interval factor method (IFM) is a nonprobabilistic mean to solve the uncertain problems with high efficiency, which has been used to calculate both the natural frequency and modal shape of structure considering interval uncertainty [2, 6-7].

In this project, via equating the interval uncertain elastic joint into spatial beam element with interval uncertain material parameters (both Young’s Modulus $E$ and Poisson’s Ratio $\mu$), a high-efficiency method to calculate the natural frequency of structure considering elastic joint with interval uncertainty on the basis of both FIMSM and IFM is developed, which is named as FIMS-IFM and verified through simulation. All the conclusions drawn from this work are of great significance to analyze engineering problems.

2. Natural frequency of structure considering uncertain elastic joint

Assume that a complex structure-$A$ is composed of two parts (namely $P$ and $Q$ respectively), and the two parts are connected via elastic joint with uncertainty (namely $p_i~q_i$, $i=$1, 2,…, $n$). Thus, structure-$A$ considering elastic joint can be illustrated as Fig. 1.

In general, when we use FIMSM to calculate the natural frequency of structure-$A$, it can be divided into two substructures, namely substructure-$P$ and substructure-$Q$, according to the substructure division principle of mode synthesis method. The interface node sets of substructure-$P$ and substructure-$Q$ are as follows:

where $P_v$ and $Q_v$ are the interface node sets of substructure-$P$ and substructure-$Q$, respectively.

Fig. 1A schematic diagram of structure-A

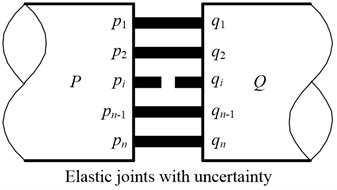
Fig. 2A schematic diagram of substructures

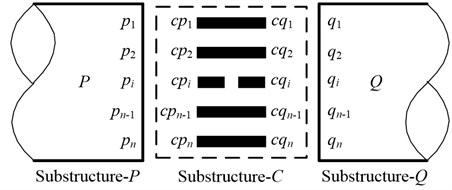
Due to the existence of the elastic joint between substructure-$P$ and substructure-$Q$, the displacement of node $p_i$ is not equal to it of node $q_i$. In such situation, therefore, the analysis results, obtained according to FIMSM, are imprecise. Nevertheless, this problem can be solved via dividing the elastic joint as an independent substructure, namely substructure-$C$. As a result, for obtaining more precise analysis results, we divide structure-$A$ into three independent substructures as shown in Fig. 2.

After the substructure division is completed, based on the working principle of FIMSM, it is easy to obtain the mass matrix, stiffness matrix and mode set of substructure-$\lambda$ ($\lambda =P$, $Q$) as ${\mathbf{M}}^{\lambda }$, ${\mathbf{K}}^{\lambda }$ and ${\mathbf{\phi }}^{\lambda }$, respectively. In addition, the mode set ${\mathbf{\phi }}^{\lambda }$ is composed of both the reserved normal mode set ${\mathbf{\phi }}_n^{\lambda }$and constrained mode set ${\mathbf{\phi }}_c^{\lambda }$ of substructure-$\lambda$ [4, 5]. As to the elastic joint, its stiffness can be equaled via the stiffness matrix of spatial beam element since substructure-$C$ owns only interface nodes [8]. Meanwhile, the stiffness uncertainty of the elastic joint can be simulated by the uncertainty of the material parameters (both Young’s Modulus $E$ and Poisson’s Ratio $\mu$) of spatial beam element. The stiffness matrix of spatial beam element ${\mathbf{K}}_b$ is given by:

where both ${\mathbf{K}}_{b1}$ and ${\mathbf{K}}_{b2}$ are deterministic matrices. As a consequence, the stiffness matrix of substructure-$C$${\mathbf{K}}^C$ can be written as:

where $\mathbf{G}$ is a deterministic transformation matrix, both ${\mathbf{K}}_1^C$ and ${\mathbf{K}}_2^C$ are deterministic matrices as well. Regarding to the mass of the elastic joint, it can be ignored because of the little effect on the dynamic properties of structure. As a result, the mass matrix of substructure-$C$${\mathbf{M}}^C$ equals $0$ [8]. At the same time, we can obtain the mode set of substructure-$C$${\mathbf{\phi }}^{\lambda }$ is an identity matrix [5].

From what has been discussed above, the mass matrix $\mathbf{M}$, stiffness matrix $\mathbf{K}$, mode set $\mathbf{\phi }$ and displacement vector $\mathbf{X}$ of structure-$A$ can be obtained as:

where ${\mathbf{X}}_u^{\lambda }$ and ${\mathbf{X}}_v^{\lambda }$ denote the displacement vector of the internal nodes and interface nodes of substructure-$\lambda$ respectively, ${\mathbf{X}}_v^{C\lambda }$ yields the displacement vector of the interface nodes of substructure-$C$ corresponding to substructure-$\lambda$. Thus, the modal coordinate $\mathbf{Y}$ corresponding to the mode set $\mathbf{\phi }$ can be given by:

where ${\mathbf{Y}}_n^{\lambda }$ and ${\mathbf{Y}}_c^{\lambda }$ are the modal coordinates corresponding to the reserved normal mode set ${\mathbf{\phi }}_n^{\lambda }$and constrained mode set ${\mathbf{\phi }}_c^{\lambda }$of substructure-$\lambda$ respectively, ${\mathbf{Y}}_c^{C\lambda }$ is the constrained mode set of substructure-$C$ corresponding to substructure-$\lambda$. The displacement coordination condition of interface connecting is given by:

where both ${\mathbf{L}}_P$ and ${\mathbf{L}}_Q$ are coordinate rotation transformation matrices. A meaningful result can be achieved from Eqs. (4-6) that:

From Eq. (7) we can obtain that, the element of modal coordinate $\mathbf{Y}$ is not independent of each other, thus, to transform the modal coordinate $\mathbf{Y}$ into an independent modal coordinate set is necessary in FIMSM. The modal coordinate transformation relationship is given by:

where $\mathbf{S}$ is the modal coordinate transformation matrix and $\mathbf{Z}$ is the independent modal coordinate. As a result, the modal mass matrix ${\mathbf{M}}_Z$ and modal stiffness matrix ${\mathbf{K}}_Z$ corresponding to $\mathbf{Z}$ can be obtained as:

As a consequence, the vibration equation of structure-$A$, obtained on the basis of FIMSM, can be present as:

The mode set $\mathbf{\Phi }$ of the vibration equation shown in Eq. (10) is given by:

where ${\mathbf{\Phi }}_i$ is the $i$th order mode. Then according to Rayleigh Quotient we can achieve the $i$th order angular frequency ${\omega }_i$ of structure-$A$ as:

where ${\mathbf{K}}_1$, ${\mathbf{K}}_2$ and ${\mathbf{K}}_3$are all deterministic matrices, the expressions of whom are as follows:

3. Interval natural frequency of structure considering interval uncertain elastic joint

As mentioned above, we use the interval uncertainty of both Young’s Modulus $E$ and Poisson’s Ratio $\mu$ of the spatial beam element to simulate the interval uncertainty of the stiffness of elastic joint, thus, in Eq. (12), both $E$ and $\mu$ are interval parameters. Meanwhile, assuming $e=1+\mu$, then $e$ is an interval parameter as well. Based on IFM [7], an interval parameters can be redefined as the product form of its interval center value and interval factor. As a result, the three interval parameters $E$, $\mu$ and $e$ can be rewritten as:

where ${\left(\right)}^C$ and ${\left(\right)}^I$ denote the interval center value and interval factor of the interval parameter $\left(\right)$ respectively, the calculation formulas of whom can be found in reference [7]. Additionally, in the right side of Eq. (12), ${\mathbf{\Phi }}_i$ holds interval uncertainty as well, thus, we can obtain that:

Then by substituting Eq. (14-15) into Eq. (12) we can achieve that:

where ${\omega }_{i1}^2$, ${\omega }_{i2}^2$ and ${\omega }_{i3}^2$ are all deterministic values, the expressions of whom are as follows:

Based on interval analysis method, therefore, we can obtain the interval lower limit $f_i^l$ and upper limit $f_i^u$ of the $i$th order natural frequency $f_i$ of structure-$A$ as follows:

where $\delta \left(\right)$ yields the relative uncertainty the interval parameter $\left(\right)$ [7].

4. Simulation

A special structure with interval uncertain elastic joint, as illustrated in Fig. 3, is designed to verify the proposed FIMS-IFM via using both FIMS-IFM and Monte-Carlo simulation method to calculate the natural frequency of the designed structure.

Fig. 3A schematic diagram of the designed structure

In Fig. 3, $P$ and $Q$ are the exactly same two rectangular cross-section beams (0.02×0.04 m² in cross-section area and 0.5 m in length); $C$ is the elastic joint with interval uncertainty which is simulated by two same circular cross-section short beams (0.005 m in cross-section diameter and 0.05 m in length) with interval uncertain Young’s Modulus $E$ and Poisson’s Ratio $\mu$. Spatial beam element is used to mesh $P$, $Q$, $C$ and the whole designed structure. The element properties of the deterministic structures $P$ and $Q$ and the interval uncertain structure $C$ are listed in Table 1 and Table 2, respectively.

By using FIMS-IFM to calculate the natural frequency, the designed structure is divided into three substructures (namely substructure-$P$, substructure-$Q$ and substructure-$C$), and the former 20 order normal modes of both substructure-$P$ and substructure-$Q$ are taken as the reserved normal mode set of corresponding substructure.

As to using Monte-Carlo simulation method, firstly, assuming that the interval parameters $E$ and $\mu$ are all uniform distributions; secondly, randomly generating 20000 samples within the distribution interval of the two assumed uniform distributions; thirdly, substituting the 20000 samples into the finite element model of the whole designed structure respectively and then calculating the natural frequency 20000 times; lastly, choosing the interval lower limit and upper limit of the interval natural frequency of the designed structure within the 20000 calculation results. Meanwhile, the two assumed uniform distributions are as follows:

The calculation results of the former 5 order natural frequencies corresponding to both FIMS-IFM and Monte-Carlo simulation method are demonstrated in Table 3.

In Table 3, $F^l$($M^l$) and $F^u$($M^u$) denote the interval lower limit and upper limit of the calculation results corresponding to FIMS-IFM (Monte-Carlo simulation method), respectively; ${\epsilon }^l$ and ${\epsilon }^u$ yield the relative calculation errors of the interval lower limit and upper limit regarding to FIMS-IFM respectively, whose calculation formulas are as follows:

As a result, by observing Table 3 we can obtain that, as to the former 5 order natural frequencies of the designed structure considering elastic joint with interval uncertainty, the relative calculation errors of the interval lower limit and upper limit regarding to the proposed highly efficient method are within 0.099 % and 0.094 % respectively, which can be strongly proved the validity of FIMS-IFM.

5. Conclusions

Via using the spatial beam element with interval uncertain material parameters to simulate the elastic joint with interval uncertainty in complex structure, FIMS-IFM, according to both FIMSM and IFM, is proposed to calculate the natural frequency of the complex structure considering elastic joint with interval uncertainty. The simulation results illustrate that, FIMS-IFM is highly efficient and correct.