Two-mass linear vibratory conveyor with reduced vibration transmission to the ground

2.1. Determination of the conveyors dynamic model

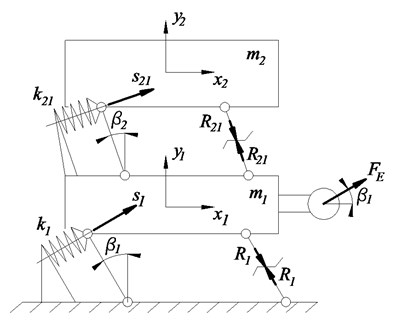
The assembly of the following two-mass vibratory conveyor consists of three principal parts, the conveying element build as a conveying trough, represented by character $m_2$, the excited mass with the drive, represented by character $m_1$ and a supporting element, fixed to the ground. Both masses are connected by the use of springs. In this case, helical springs are chosen. The excitation of $m_1$ is done by an eccentric drive, installed to excite the mass 90° to the lever $R_1$ [4]. The springs with their particular stiffness are defined as $k_1$ and $k_{21}$. The damping of the system is neglected. Mass $m_1$ is connected to the ground by levers under an angle ${\beta }_1$, mass $m_2$ is connected to mass $m_1$ by levers under an angle ${\beta }_2$. The levers enabling a defined guidance of the masses motion. Fig. 2 shows the mechanical model of this two-mass conveyor.

Fig. 2Mechanical model of the vibratory conveyor

2.2. Calculation of dynamic parameters

Based on the mechanical model shown in Fig. 2, the following equations are formed [5]:

Summing up the Eqs. (1) and (3), (2) and (4) as well as (3) and (4), the following equations can be formed:

Merging Eqs. (5) and (6), the equation can be formed as:

and after converting Eq. (8):

Splitting up the motion of $x_2$ and $y_2$into the components, the following form can be written:

The levers guide the motion of each of the two masses between floor and mass $m_1$ and between mass $m_1$and mass $m_2$. Therefore, the coordinate vectors with the characters $x$ and $y$ can be merged and replaced by character $s$.

Then the Eqs. (10) and (11) can be formed as:

with

After simplifying the Eqs. (12) and (13), the final equations of motion for the analyzed conveyor model are:

3.1. Variation of the angles of the dynamic model

For the further analysis of the dynamic model, three cases are of particular interest:

– Case one with ${\beta }_1={\beta }_2$,

– Case two with ${\beta }_1=0$ and

– Case three with ${\beta }_2=0$.

For case one with ${\beta }_1={\beta }_2$, Eq. (15) can be converted step by step:

to the final form:

Eq. (16) is transformed by the same way into the final form:

For case two with ${\beta }_1=0$, the equations are:

For case three with ${\beta }_2=0$, the following equations can be formed:

3.2. Calculation of the displacement

To find the zero displacement $s_{10}$ of mass $m_1$and the maximum displacement $s_{20}$, of mass $m_2$, the corresponding equations for case ${\beta }_1={\beta }_2$ can be formed as:

Eq. (26) can be adjusted in a way that $s_{10}$ will become zero. For that case, the minimum transmission of forces to the floor is achieved [6, 7].

Based on this dynamical model, the minimum transmission of vibration and forces to the floor is achieved. As soon as mass $m_1$ remains stationary, the total excitation is passed over to the absorber mass $m_2$, supplying the optimum conveying of goods [8].